第八单元数与形-六年级上册数学单元易错精讲精练人教版(含解析)
文档属性
| 名称 | 第八单元数与形-六年级上册数学单元易错精讲精练人教版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-28 16:07:01 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第八单元数与形-六年级上册数学单元易错精讲精练人教版
易错精讲
易错题一:
【例1】
请根据下图中的规律,按要求回答问题。
(1)在下表中完整地填写③、④号图的相关数据。
图号 ① ② ③ ④
白色三角形个数 0 1
黑色三角形个数 1 3
总个数
(2)根据以上的信息,你发现了什么规律?
(3)当黑色三角形个数比白色三角形个数多10个时,白色三角形和黑色三角形的总个数是多少个?黑色的多少个?
答案:(1)3;6;6;10;;;
(2)第n个图形黑色三角形个数比白色三角形个数多n个,总个数为n2;
(3)100个;55个
【分析】(1)图①白色三角形为0个,黑色三角形为1个,三角形的总个数为12;图②白色三角形为1个,黑色三角形为(1+2)个,三角形的总个数为22;图③白色三角形为(1+2)个,黑色三角形为(1+2+3)个,三角形的总个数为32;图④白色三角形为(1+2+3)个,黑色三角形为(1+2+3+4)个,三角形的总个数为42……
(2)由表格可知,图①黑色三角形个数比白色三角形个数多1个,总个数为12;图②黑色三角形个数比白色三角形个数多2个,总个数为22;图③黑色三角形个数比白色三角形个数多3个,总个数为32;图④黑色三角形个数比白色三角形个数多4个,总个数为42……
(3)由规律可知,当黑色三角形个数比白色三角形个数多10个时,三角形的总个数为100个,黑色三角形的个数=(三角形的总个数+两种三角形个数的差)÷2;据此解答。
【详解】(1)
图号 ① ② ③ ④
白色三角形个数 0 1 3 6
黑色三角形个数 1 3 6 10
总个数
(2)分析可知,第n个图形黑色三角形个数比白色三角形个数多n个,总个数为n2。
(3)当黑色三角形个数比白色三角形个数多10个时,黑白三角形的总个数为102=100(个)
(100+10)÷2
=110÷2
=55(个)
答:白色三角形和黑色三角形的总个数是100个,黑色的55个。
【点睛】分析图形和表格找出三角形个数变化的规律是解答题目的关键。
易错题二:
【例2】
下面的4个图形都是用相同的小棒拼成的。
①根据前4个图形的规律拼摆,40根小棒能摆出第10个图形吗?
②第n个图形是由多少根小棒拼成的?把探索过程用你喜欢的方式表示出来。
答案:①不能
②4n+1根;过程见详解
【分析】观察可知,图形数量=(小棒数量-1)÷4;小棒数量=图形数量×4+1,据此分析。
【详解】①10×4+1
=40+1
=41(根)
41>40
答:不能摆出第10个图形。
②第1个图形用5根小棒,5=1×4+1
第2个图形用9根小棒,9=2×4+1
第3个图形用13根小棒,13=3×4+1
第4个图形用17根小棒,17=4×4+1
所以小棒数量=4n+1(根)
【点睛】数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
易错题三:
【例3】
一张桌子摆4把椅子,两张桌子并起来摆6把椅子……照这样摆下去。
(1)6张桌子可以摆多少把椅子?
(2)n张桌子可以摆多少把椅子?用式子表示出来是( )把。
(3)如果有34人,需要并起来多少张桌子才能坐下?
答案:(1)14把;
(2)2n+2;
(3)16张
【分析】由图可知,1张桌子时,可以摆4把椅子;2张桌子时,可以摆(4+2)把椅子;3张桌子时,可以摆(4+2+2)把椅子……每增加一张桌子就增加2把椅子,那么n张桌子时,可以摆4+2(n-1)把椅子;最后计算出椅子数量为34时,n的值即可。
【详解】(1)1张桌子可以摆椅子的数量:4把
2张桌子可以摆椅子的数量:4+2=6(把)
3张桌子可以摆椅子的数量:4+2×2=4+4=8(把)
4张桌子可以摆椅子的数量:4+3×2=4+6=10(把)
5张桌子可以摆椅子的数量:4+4×2=4+8=12(把)
6张桌子可以摆椅子的数量:4+5×2=4+10=14(把)
答:6张桌子可以摆14把椅子。
(2)分析可知,n张桌子可以摆椅子的数量:4+2(n-1)=4+2n-2=(2n+2)把
(3)如果有34人,那么需要34把椅子。
2n+2=34
解:2n=34-2
2n=32
n=32÷2
n=16
答:如果有34人,需要并起来16张桌子才能坐下。
【点睛】分析题意找出椅子数量变化的规律是解答题目的关键。
易错题四:
【例4】
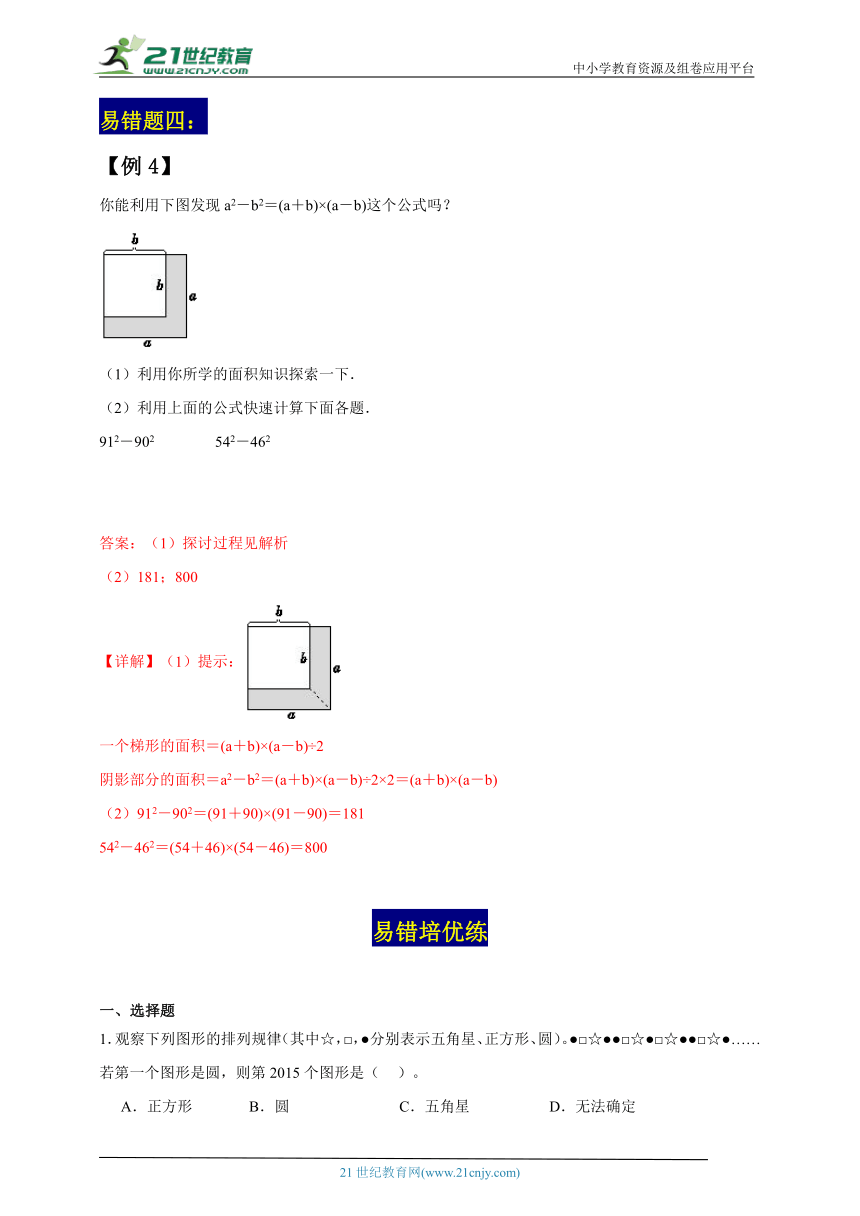
你能利用下图发现a2-b2=(a+b)×(a-b)这个公式吗?
(1)利用你所学的面积知识探索一下.
(2)利用上面的公式快速计算下面各题.
912-902 542-462
答案:(1)探讨过程见解析
(2)181;800
【详解】(1)提示:
一个梯形的面积=(a+b)×(a-b)÷2
阴影部分的面积=a2-b2=(a+b)×(a-b)÷2×2=(a+b)×(a-b)
(2)912-902=(91+90)×(91-90)=181
542-462=(54+46)×(54-46)=800
易错培优练
一、选择题
1.观察下列图形的排列规律(其中☆,□,●分别表示五角星、正方形、圆)。●□☆●●□☆●□☆●●□☆●……若第一个图形是圆,则第2015个图形是( )。
A.正方形 B.圆 C.五角星 D.无法确定
2.仔细观察前两幅图,并根据规律写出第三幅图所表示的数是( )。
A.21341 B.200013041 C.200013401 D.200010341
3.如图,按这样的规律接着画下去,第六个图形中有( )个■。
A.30 B.36 C.42 D.48
4.用小棒按照如下方式摆图形,摆n个八边形需要( )根小棒。
A.8n B.8n-1 C.7n+1 D.8(n-1)
5.按如图所示的方式排列点阵,则第六个点阵中有( )个点。
A.16 B.21 C.25 D.36
6.“龟兔赛跑”中兔子跑得快,一开始领先,但它太骄傲在途中睡了一觉再继续跑;乌龟跑得慢,但一直不停地跑,抵达终点,赢得胜利。下面哪幅图基本反映了比赛的过程?( )。
A. B.
C. D.
二、填空题
7.〇〇☆☆☆〇〇☆☆☆〇〇☆☆☆……排列,左起第22个是( ),前50个图形中,☆有( )个。
8.“2022北京冬奥会”某国代表团安排入住奥运村C区宿舍,若每间2人,则有12人没有床位:若每间3人,则多出2个空床位,C区共有宿舍( )间,运动员共有( )。
9.先观察,再按规律填一填。
1=12 1+3=22 1+3+5=32
1+3+5+7=( )2
1+3+5+7+9+11+13=( )2
10.从如图中点的排列规律可以看出,第8个图共有( )个点,第n个图共有( )个点。
11.如果按照下面的画法,画到第10个正方形时,图中共有( )个直角三角形。
12.《庄子·天下》中有这样一段话:“一尺之锤,日取其半,万世不竭。”意思是说:一尺长的木棍,每天截取一半,永远也截不完。照这样下去,第四天截取的长度占最初木棍长度的( )。
13.照下面的规律画下去,第4个图形有( )个小△,第n个图形有( )个小△。
14.如图所示,第①幅图有2颗☆,第②幅图有8颗☆,第③幅图有18颗☆。
(1)第④幅图有( )颗☆。
(2)当有200颗☆时,这是第( )幅图。
三、解答题
15.像下图那样用小棒摆三角形,请你算一算。摆10个三角形用多少根小棒?摆n个三角形呢?
16.牛牛突然他想起今天中午吃饭的时候,餐厅贴出来的菜单:
水 煮 鱼 水 煮 鱼 水 煮 鱼 水 煮 ……
宫 保 鸡 丁 宫 保 鸡 丁 宫 保 鸡 ……
如图所示,每列上、下两个字组成一组,例如,第一组是“水宫”,第二组是“煮保”,请写出第45组是什么?
17.用同样大小的黑色棋子按如图所示的规律摆放:
(1)第8个图形中有多少颗黑色棋子?
(2)第几个图形中有303颗黑色棋子?
18.现有若干个圆环,它的外直径是5厘米,环宽是0.5厘米,将它们(如下图)扣在一起,拉紧后测量其长度,请完成表格。
圆环个数 1 2 3 4 5 6 ……
拉紧后的长度/cm
(1)请完成表格。
(2)根据表中规律,11个圆环拉紧后的长度是多少厘米?
(3)设圆环的个数为a,拉紧后的总长度为S,你能用一个关系式表示你发现的规律吗?
(4)若拉紧后的长度是77厘来,则它是由多少个圆环扣成的?
19.
(1)按这样的规律摆下去,第n个图形需要多少个●?
(2)按上面的规律,摆第几个图形需要用200个●?
参考答案:
1.A
【分析】观察图形可知,圆、正方形、五星、圆、圆、正方形、五星,7个一组为一循环周期,即个数能被7整除的图形为五角星;不能整数余数为1、2、3、4、5、6的图形分别为圆、正方形、五角星、圆、圆、正方形;由此可知,余数是几,就是第几个图形,据此解答。
【详解】2015÷7=287……6
2015个图形是正方形。
观察下列图形的排列规律(其中☆,□,●分别表示五角星、正方形、圆)。●□☆●●□☆●□☆●●□☆●……若第一个图形是圆,则第2015个图形是正方形。
故答案为:A
2.C
【分析】根据前两幅图可知,有几只表示几个亿,有几个表示几个万;有几个有几个百,有几只表示几个千,有几个表示几个1,据此解答。
【详解】根据分析可知,第三幅图有2个亿、1个万、3个千、4个百和1个1,所以第三幅图所表示的数是200013401。
仔细观察前两幅图,并根据规律写出第三幅图所表示的数是200013401。
故答案为:C
【点睛】观察各个图中每种动物的数量与写作的大数中每个数位上的数,是解答本题的关键。
3.D
【分析】看图可知,第一个图形有8个黑色正方形,第二个图形有16个黑色正方形,第三个图形有24个黑色正方形。以此列推,可以得出规律:第一个图形有8×1个黑色正方形,第二个图形有8×2个黑色正方形,第三个图形有8×3个黑色正方形,所以第n个图形有8×n个黑色正方形。
【详解】根据规律可知,第六个图形中的黑色正方形有:8×6=48(个)
故答案为:D
【点睛】此题考查了学生的逻辑思维能力,关键是找到规律。
4.C
【分析】根据图示发现:摆1个八边形需要小棒:8根;摆2个八边形需要小棒(8+7)根;摆3个八边形需要小棒(8+7+7)根;……摆n个八边形需要小棒的根数是8+7(n-1)。据此解答。
【详解】8+7(n-1)
=8+7n-7
=(7n+1)根
摆n个八边形需要(7n+1)根小棒。
故答案为:C
【点睛】本题主要考查数与形结合的规律,关键根据图示发现这组图形的规律,并运用规律做题。
5.D
【分析】观察图形可知:
第1个图形有1个点,1=12;
第2个图形有1+3=4个点,4=22;
第3个图形有1+3+5=9个点,9=33;
……
第n个图形有n2个点;
据此规律解答。
【详解】规律:第n个图形有n2个点;
当n=6时,n2=62=36;
则第六个点阵中有36个点。
故答案为:D
【点睛】通过数与形的结合,从已知的图形或数据中找到规律,并按规律解题。
6.B
【分析】由图可知,横轴表示时间,纵轴表示路程,实线表示兔子的比赛过程,虚线表示乌龟的比赛过程,折线越陡速度越快,折线越缓速度越慢,据此逐项分析。
【详解】A.兔子跑完全程用的时间比乌龟跑完全程用的时间少,则兔子先到达终点,错误;
B.一开始兔子比乌龟的速度快,中途兔子睡完觉后继续跑,最后乌龟跑完全程用的时间比兔子跑完全程用的时间短,乌龟先到达终点,正确;
C.一开始乌龟的速度比兔子的速度快,乌龟领先,不符合题意,错误;
D.最后乌龟和兔子同时到达终点,乌龟没有赢得胜利,错误。
故答案为:B
【点睛】理解图中每段折线表示的意义是解答题目的关键。
7. 〇 30
【分析】每5个图形一循环,计算第22个,第50个图形是第几组循环零几个图形,即可判断最后一个的形状及五角星的个数。
【详解】22÷5=4(组)……2(个)
50÷5=10(组)
10×3=30(个)
左起第22个是〇,前50个图形中,☆有30个。
【点睛】先找到规律,再根据规律求解。
8. 14 40
【分析】根据题意,当每个房间增加3-2=1个人的时候,原来12个没有床位的人有了床位,还多出2个床位来,也就是说,每个房间增加一个床位,就会多出12+2=14个床位,所以一共有(12+2)÷(3-2)间房,再根据题意可求出总人数。
【详解】根据题意可得宿舍的间数:(12+2)÷(3-2)
=14÷1
=14(间)
那么运动员的人数为:14×2+12
=28+12
=40(人)
“2022北京冬奥会”某国代表团安排入住奥运村C区宿舍,若每间2人,则有12人没有床位:若每间3人,则多出2个空床位,C区共有宿舍14间,运动员共有40。
【点睛】此题考查了学生的理解分析能力和整数的四则运算。
9. 4 7
【分析】结合图与算式,先找出算式与计算结果的规律,算式中加数的大小规律是:第一个加数是1,第二个加数是3,后面每个加数增加2,计算结果的规律是加数个数的平方。
【详解】通过观察图形及图形对应的算式可以发现:算式左边是从1开始连续奇数的和,算式右边数是左边有几个奇数,它们的和就是几的平方。
1+3+5+7相加,有4个奇数,所以为4的平方,1+3+5+7+9+11+13相加,有7个奇数,所以为7的平方。
综上所述:1+3+5+7=42
1+3+5+7+9+11+13=72
【点睛】本题是探索算数规律的题目,关键是利用数形结合的思想寻找算式中的规律。
10. 25 3n+1/1+3n
【分析】观察可知,点的数量=第几个图形就用几×3+1,据此分析。
【详解】8×3+1
=24+1
=25(个)
第8个图共有25个点;即第n个图有(3n+1)个点。
【点睛】数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
11.36
【分析】观察图形可知:
1个正方形有0个直角三角形,0=1×4-4;
2个正方形有4个直角三角形,4=2×4-4;
3个正方形有8个直角三角形,8=3×4-4;
4个正方形有12个直角三角形,12=4×4-4;
5个正方形有16个直角三角形,16=5×4-4;
……
按此规律摆下去,n个正方形有(4n-4)个直角三角形。
【详解】规律:n个正方形有(4n-4)个直角三角形。
当n=10时
4n-4
=4×10-4
=40-4
=36(个)
画到第10个正方形时,图中共有36个直角三角形。
【点睛】通过数与形的结合,从已知的图形或数据中找到规律,并按规律解题。
12.
【分析】根据题意,每天截取一半,则每次截取的和剩下的一样多,第一天截取的是木棍总长度的,第二天截取的是的,即×=,第三天截取的是的,即:×=,以此类推,可得第n天截取的长度占最初木棍长度的分率为n个的乘积;据此解答。
【详解】根据分析:
×××
=×
=
所以,照这样下去,第四天截取的长度占最初木棍长度的。
【点睛】此题考查了分数乘法与加法的综合应用,明确求一个数的几分之几用乘法计算。
13. 16 n2
【分析】观察图形可知:
第1个图形有1个△,1=12;
第2个图形有4个△,4=22;
第3个图形有9个△,9=32;
……
第n个图形有n2个△;
据此找到规律并解答。
【详解】第4个图形有△的个数:42=16(个)
第n个图形有n2个△。
【点睛】通过数与形的结合,从已知的图形或数据中找到规律,并按规律解题。
14.(1)32
(2)⑩
【分析】第①幅图中☆的颗数表示成;第②幅图中☆的颗数表示成2+4+2=2×4=2×22;第③幅图中☆的颗数表示成2+4+6+4+2=2×9=2×32;……;由此可得。第④幅图中☆的颗数是2×42=32(颗);当有200颗☆时,200÷2=100(颗),100=10×10,故第⑩幅图中有200颗☆。
【详解】(1)2×42=32(颗)
(2)200÷2=100(颗),100=10×10
【点睛】本题主要考查学生的推理能力,关键要发现其中的规律。
15.21根;(2n+1)根
【分析】根据图示发现:摆1个三角形需要小棒:(1+2)根;摆2个三角形需要小棒:(1+2+2)根;摆3个三角形需要小棒:(1+2+2+2)根;依次类推……摆n个三角形需要小棒:(2×n+1)根。据此解答。
【详解】摆n个三角形需要小棒:2×n+1=(2n+1)根
当n=10时,
2×10+1
=20+1
=21(根)
答:摆10个三角形用21根小棒;摆n个三角形用(2n+1)根小棒。
【点睛】本题主要考查数与形结合的规律,关键根据图示发现这组图形的规律,并运用规律做题。
16.鱼宫
【分析】观察表格可知,第一排是按照水、煮、鱼 3个一组循环排列的;第二排是按照宫、保、鸡、丁 4个一组循环排列的,用45分别除以3和4,余数是几就从左边数几即可。
【详解】45÷3=15(组)
45÷4=11(组) 1(个)
答:第45组上面的字是鱼,下面的字是宫。
【点睛】本题考查循环数列,明确上、下几个字为一组是解题的关键。
17.(1)27颗(2)100个
【分析】第1图形有黑色棋子的颗数:6=1×3+3;
第2图形有黑色棋子的颗数:9=2×3+3;
第3图形有黑色棋子的颗数:12=3×3+3;
第4图形有黑色棋子的颗数:15=4×3+3;
……
第n图形有黑色棋子的颗数:n×3+3。
【详解】(1)8×3+3
=24+3
=27(颗)
答:第8个图形中有27颗黑色棋子。
(2)(303-3)÷3
=300÷3
=100(个)
答:第100个图形中有303颗黑色棋子。
【点睛】解题关键是通过归纳与总结,得到其中的规律,再灵活运用规律解答。
18.(1)见详解
(2)45厘米
(3)S=1+4a;
(4)19个
【分析】(1)根据题干可知,1个圆环的长度是5厘米,以后每增加一个圆环,就增加5-0.5×2=4厘米,由此可以完成表格,
(2)观察上表格可得:当有n个圆环,拉紧后的总长度就是:1+4n厘米,由此进行解答;
(3)依据上面规律,代入数据即可得出用字母a、S表示的关系式;
(4)设有n个圆环扣成的,由上面得出的关系式即可得出一个方程,解方程即可。
【详解】(1)1个圆环的长度是5厘米,以后每增加一个圆环,就增加5-0.5×2=4厘米,由此可以完成表格:
圆环个数 1 2 3 4 5 6 ……
拉紧后的长度/cm 5 9 13 17 21 25 ……
(2)观察上表格可得:当有n个圆环,拉紧后的总长度就是:1+4n厘米,
所以,当n=11时,总长度为:
1+11×4
=1+44
=45(厘米)
答:11个圆环拉紧后的长度是45厘米。
(3)设圆环的个数为a,拉紧后的总长度为S,则可得圆环与拉紧后的总长度的关系式:
S=0.5×2+(5-0.5×2)a
=1+4a
答:关系式为:S==1+4a
(4)解:设圆环的个数为x,根据上面关系式可得:
1+4x=77
4x=76
X=19
答:是由19个圆环扣成的。
【点睛】此题考查是的找规律,正确找出规律并用规律解决问题是解题关键。
19.(1)4n个
(2)50个
【分析】第1个图形中有●的个数:4个,4=1×4;
第2个图形中有●的个数:8个,8=2×4;
第3个图形中有●的个数:12个,12=3×4;
……
第n个图形中有●的个数:4n个。
【详解】(1)4×n=4n(个)
答:第n个图形需要4n个●。
(2)200÷4=50(个)
答:摆第50个图形需要用200个●。
【点睛】本题是找规律的题型,从已知的图形或数据中找到规律,并按规律解题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第八单元数与形-六年级上册数学单元易错精讲精练人教版
易错精讲
易错题一:
【例1】
请根据下图中的规律,按要求回答问题。
(1)在下表中完整地填写③、④号图的相关数据。
图号 ① ② ③ ④
白色三角形个数 0 1
黑色三角形个数 1 3
总个数
(2)根据以上的信息,你发现了什么规律?
(3)当黑色三角形个数比白色三角形个数多10个时,白色三角形和黑色三角形的总个数是多少个?黑色的多少个?
答案:(1)3;6;6;10;;;
(2)第n个图形黑色三角形个数比白色三角形个数多n个,总个数为n2;
(3)100个;55个
【分析】(1)图①白色三角形为0个,黑色三角形为1个,三角形的总个数为12;图②白色三角形为1个,黑色三角形为(1+2)个,三角形的总个数为22;图③白色三角形为(1+2)个,黑色三角形为(1+2+3)个,三角形的总个数为32;图④白色三角形为(1+2+3)个,黑色三角形为(1+2+3+4)个,三角形的总个数为42……
(2)由表格可知,图①黑色三角形个数比白色三角形个数多1个,总个数为12;图②黑色三角形个数比白色三角形个数多2个,总个数为22;图③黑色三角形个数比白色三角形个数多3个,总个数为32;图④黑色三角形个数比白色三角形个数多4个,总个数为42……
(3)由规律可知,当黑色三角形个数比白色三角形个数多10个时,三角形的总个数为100个,黑色三角形的个数=(三角形的总个数+两种三角形个数的差)÷2;据此解答。
【详解】(1)
图号 ① ② ③ ④
白色三角形个数 0 1 3 6
黑色三角形个数 1 3 6 10
总个数
(2)分析可知,第n个图形黑色三角形个数比白色三角形个数多n个,总个数为n2。
(3)当黑色三角形个数比白色三角形个数多10个时,黑白三角形的总个数为102=100(个)
(100+10)÷2
=110÷2
=55(个)
答:白色三角形和黑色三角形的总个数是100个,黑色的55个。
【点睛】分析图形和表格找出三角形个数变化的规律是解答题目的关键。
易错题二:
【例2】
下面的4个图形都是用相同的小棒拼成的。
①根据前4个图形的规律拼摆,40根小棒能摆出第10个图形吗?
②第n个图形是由多少根小棒拼成的?把探索过程用你喜欢的方式表示出来。
答案:①不能
②4n+1根;过程见详解
【分析】观察可知,图形数量=(小棒数量-1)÷4;小棒数量=图形数量×4+1,据此分析。
【详解】①10×4+1
=40+1
=41(根)
41>40
答:不能摆出第10个图形。
②第1个图形用5根小棒,5=1×4+1
第2个图形用9根小棒,9=2×4+1
第3个图形用13根小棒,13=3×4+1
第4个图形用17根小棒,17=4×4+1
所以小棒数量=4n+1(根)
【点睛】数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
易错题三:
【例3】
一张桌子摆4把椅子,两张桌子并起来摆6把椅子……照这样摆下去。
(1)6张桌子可以摆多少把椅子?
(2)n张桌子可以摆多少把椅子?用式子表示出来是( )把。
(3)如果有34人,需要并起来多少张桌子才能坐下?
答案:(1)14把;
(2)2n+2;
(3)16张
【分析】由图可知,1张桌子时,可以摆4把椅子;2张桌子时,可以摆(4+2)把椅子;3张桌子时,可以摆(4+2+2)把椅子……每增加一张桌子就增加2把椅子,那么n张桌子时,可以摆4+2(n-1)把椅子;最后计算出椅子数量为34时,n的值即可。
【详解】(1)1张桌子可以摆椅子的数量:4把
2张桌子可以摆椅子的数量:4+2=6(把)
3张桌子可以摆椅子的数量:4+2×2=4+4=8(把)
4张桌子可以摆椅子的数量:4+3×2=4+6=10(把)
5张桌子可以摆椅子的数量:4+4×2=4+8=12(把)
6张桌子可以摆椅子的数量:4+5×2=4+10=14(把)
答:6张桌子可以摆14把椅子。
(2)分析可知,n张桌子可以摆椅子的数量:4+2(n-1)=4+2n-2=(2n+2)把
(3)如果有34人,那么需要34把椅子。
2n+2=34
解:2n=34-2
2n=32
n=32÷2
n=16
答:如果有34人,需要并起来16张桌子才能坐下。
【点睛】分析题意找出椅子数量变化的规律是解答题目的关键。
易错题四:
【例4】
你能利用下图发现a2-b2=(a+b)×(a-b)这个公式吗?
(1)利用你所学的面积知识探索一下.
(2)利用上面的公式快速计算下面各题.
912-902 542-462
答案:(1)探讨过程见解析
(2)181;800
【详解】(1)提示:
一个梯形的面积=(a+b)×(a-b)÷2
阴影部分的面积=a2-b2=(a+b)×(a-b)÷2×2=(a+b)×(a-b)
(2)912-902=(91+90)×(91-90)=181
542-462=(54+46)×(54-46)=800
易错培优练
一、选择题
1.观察下列图形的排列规律(其中☆,□,●分别表示五角星、正方形、圆)。●□☆●●□☆●□☆●●□☆●……若第一个图形是圆,则第2015个图形是( )。
A.正方形 B.圆 C.五角星 D.无法确定
2.仔细观察前两幅图,并根据规律写出第三幅图所表示的数是( )。
A.21341 B.200013041 C.200013401 D.200010341
3.如图,按这样的规律接着画下去,第六个图形中有( )个■。
A.30 B.36 C.42 D.48
4.用小棒按照如下方式摆图形,摆n个八边形需要( )根小棒。
A.8n B.8n-1 C.7n+1 D.8(n-1)
5.按如图所示的方式排列点阵,则第六个点阵中有( )个点。
A.16 B.21 C.25 D.36
6.“龟兔赛跑”中兔子跑得快,一开始领先,但它太骄傲在途中睡了一觉再继续跑;乌龟跑得慢,但一直不停地跑,抵达终点,赢得胜利。下面哪幅图基本反映了比赛的过程?( )。
A. B.
C. D.
二、填空题
7.〇〇☆☆☆〇〇☆☆☆〇〇☆☆☆……排列,左起第22个是( ),前50个图形中,☆有( )个。
8.“2022北京冬奥会”某国代表团安排入住奥运村C区宿舍,若每间2人,则有12人没有床位:若每间3人,则多出2个空床位,C区共有宿舍( )间,运动员共有( )。
9.先观察,再按规律填一填。
1=12 1+3=22 1+3+5=32
1+3+5+7=( )2
1+3+5+7+9+11+13=( )2
10.从如图中点的排列规律可以看出,第8个图共有( )个点,第n个图共有( )个点。
11.如果按照下面的画法,画到第10个正方形时,图中共有( )个直角三角形。
12.《庄子·天下》中有这样一段话:“一尺之锤,日取其半,万世不竭。”意思是说:一尺长的木棍,每天截取一半,永远也截不完。照这样下去,第四天截取的长度占最初木棍长度的( )。
13.照下面的规律画下去,第4个图形有( )个小△,第n个图形有( )个小△。
14.如图所示,第①幅图有2颗☆,第②幅图有8颗☆,第③幅图有18颗☆。
(1)第④幅图有( )颗☆。
(2)当有200颗☆时,这是第( )幅图。
三、解答题
15.像下图那样用小棒摆三角形,请你算一算。摆10个三角形用多少根小棒?摆n个三角形呢?
16.牛牛突然他想起今天中午吃饭的时候,餐厅贴出来的菜单:
水 煮 鱼 水 煮 鱼 水 煮 鱼 水 煮 ……
宫 保 鸡 丁 宫 保 鸡 丁 宫 保 鸡 ……
如图所示,每列上、下两个字组成一组,例如,第一组是“水宫”,第二组是“煮保”,请写出第45组是什么?
17.用同样大小的黑色棋子按如图所示的规律摆放:
(1)第8个图形中有多少颗黑色棋子?
(2)第几个图形中有303颗黑色棋子?
18.现有若干个圆环,它的外直径是5厘米,环宽是0.5厘米,将它们(如下图)扣在一起,拉紧后测量其长度,请完成表格。
圆环个数 1 2 3 4 5 6 ……
拉紧后的长度/cm
(1)请完成表格。
(2)根据表中规律,11个圆环拉紧后的长度是多少厘米?
(3)设圆环的个数为a,拉紧后的总长度为S,你能用一个关系式表示你发现的规律吗?
(4)若拉紧后的长度是77厘来,则它是由多少个圆环扣成的?
19.
(1)按这样的规律摆下去,第n个图形需要多少个●?
(2)按上面的规律,摆第几个图形需要用200个●?
参考答案:
1.A
【分析】观察图形可知,圆、正方形、五星、圆、圆、正方形、五星,7个一组为一循环周期,即个数能被7整除的图形为五角星;不能整数余数为1、2、3、4、5、6的图形分别为圆、正方形、五角星、圆、圆、正方形;由此可知,余数是几,就是第几个图形,据此解答。
【详解】2015÷7=287……6
2015个图形是正方形。
观察下列图形的排列规律(其中☆,□,●分别表示五角星、正方形、圆)。●□☆●●□☆●□☆●●□☆●……若第一个图形是圆,则第2015个图形是正方形。
故答案为:A
2.C
【分析】根据前两幅图可知,有几只表示几个亿,有几个表示几个万;有几个有几个百,有几只表示几个千,有几个表示几个1,据此解答。
【详解】根据分析可知,第三幅图有2个亿、1个万、3个千、4个百和1个1,所以第三幅图所表示的数是200013401。
仔细观察前两幅图,并根据规律写出第三幅图所表示的数是200013401。
故答案为:C
【点睛】观察各个图中每种动物的数量与写作的大数中每个数位上的数,是解答本题的关键。
3.D
【分析】看图可知,第一个图形有8个黑色正方形,第二个图形有16个黑色正方形,第三个图形有24个黑色正方形。以此列推,可以得出规律:第一个图形有8×1个黑色正方形,第二个图形有8×2个黑色正方形,第三个图形有8×3个黑色正方形,所以第n个图形有8×n个黑色正方形。
【详解】根据规律可知,第六个图形中的黑色正方形有:8×6=48(个)
故答案为:D
【点睛】此题考查了学生的逻辑思维能力,关键是找到规律。
4.C
【分析】根据图示发现:摆1个八边形需要小棒:8根;摆2个八边形需要小棒(8+7)根;摆3个八边形需要小棒(8+7+7)根;……摆n个八边形需要小棒的根数是8+7(n-1)。据此解答。
【详解】8+7(n-1)
=8+7n-7
=(7n+1)根
摆n个八边形需要(7n+1)根小棒。
故答案为:C
【点睛】本题主要考查数与形结合的规律,关键根据图示发现这组图形的规律,并运用规律做题。
5.D
【分析】观察图形可知:
第1个图形有1个点,1=12;
第2个图形有1+3=4个点,4=22;
第3个图形有1+3+5=9个点,9=33;
……
第n个图形有n2个点;
据此规律解答。
【详解】规律:第n个图形有n2个点;
当n=6时,n2=62=36;
则第六个点阵中有36个点。
故答案为:D
【点睛】通过数与形的结合,从已知的图形或数据中找到规律,并按规律解题。
6.B
【分析】由图可知,横轴表示时间,纵轴表示路程,实线表示兔子的比赛过程,虚线表示乌龟的比赛过程,折线越陡速度越快,折线越缓速度越慢,据此逐项分析。
【详解】A.兔子跑完全程用的时间比乌龟跑完全程用的时间少,则兔子先到达终点,错误;
B.一开始兔子比乌龟的速度快,中途兔子睡完觉后继续跑,最后乌龟跑完全程用的时间比兔子跑完全程用的时间短,乌龟先到达终点,正确;
C.一开始乌龟的速度比兔子的速度快,乌龟领先,不符合题意,错误;
D.最后乌龟和兔子同时到达终点,乌龟没有赢得胜利,错误。
故答案为:B
【点睛】理解图中每段折线表示的意义是解答题目的关键。
7. 〇 30
【分析】每5个图形一循环,计算第22个,第50个图形是第几组循环零几个图形,即可判断最后一个的形状及五角星的个数。
【详解】22÷5=4(组)……2(个)
50÷5=10(组)
10×3=30(个)
左起第22个是〇,前50个图形中,☆有30个。
【点睛】先找到规律,再根据规律求解。
8. 14 40
【分析】根据题意,当每个房间增加3-2=1个人的时候,原来12个没有床位的人有了床位,还多出2个床位来,也就是说,每个房间增加一个床位,就会多出12+2=14个床位,所以一共有(12+2)÷(3-2)间房,再根据题意可求出总人数。
【详解】根据题意可得宿舍的间数:(12+2)÷(3-2)
=14÷1
=14(间)
那么运动员的人数为:14×2+12
=28+12
=40(人)
“2022北京冬奥会”某国代表团安排入住奥运村C区宿舍,若每间2人,则有12人没有床位:若每间3人,则多出2个空床位,C区共有宿舍14间,运动员共有40。
【点睛】此题考查了学生的理解分析能力和整数的四则运算。
9. 4 7
【分析】结合图与算式,先找出算式与计算结果的规律,算式中加数的大小规律是:第一个加数是1,第二个加数是3,后面每个加数增加2,计算结果的规律是加数个数的平方。
【详解】通过观察图形及图形对应的算式可以发现:算式左边是从1开始连续奇数的和,算式右边数是左边有几个奇数,它们的和就是几的平方。
1+3+5+7相加,有4个奇数,所以为4的平方,1+3+5+7+9+11+13相加,有7个奇数,所以为7的平方。
综上所述:1+3+5+7=42
1+3+5+7+9+11+13=72
【点睛】本题是探索算数规律的题目,关键是利用数形结合的思想寻找算式中的规律。
10. 25 3n+1/1+3n
【分析】观察可知,点的数量=第几个图形就用几×3+1,据此分析。
【详解】8×3+1
=24+1
=25(个)
第8个图共有25个点;即第n个图有(3n+1)个点。
【点睛】数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
11.36
【分析】观察图形可知:
1个正方形有0个直角三角形,0=1×4-4;
2个正方形有4个直角三角形,4=2×4-4;
3个正方形有8个直角三角形,8=3×4-4;
4个正方形有12个直角三角形,12=4×4-4;
5个正方形有16个直角三角形,16=5×4-4;
……
按此规律摆下去,n个正方形有(4n-4)个直角三角形。
【详解】规律:n个正方形有(4n-4)个直角三角形。
当n=10时
4n-4
=4×10-4
=40-4
=36(个)
画到第10个正方形时,图中共有36个直角三角形。
【点睛】通过数与形的结合,从已知的图形或数据中找到规律,并按规律解题。
12.
【分析】根据题意,每天截取一半,则每次截取的和剩下的一样多,第一天截取的是木棍总长度的,第二天截取的是的,即×=,第三天截取的是的,即:×=,以此类推,可得第n天截取的长度占最初木棍长度的分率为n个的乘积;据此解答。
【详解】根据分析:
×××
=×
=
所以,照这样下去,第四天截取的长度占最初木棍长度的。
【点睛】此题考查了分数乘法与加法的综合应用,明确求一个数的几分之几用乘法计算。
13. 16 n2
【分析】观察图形可知:
第1个图形有1个△,1=12;
第2个图形有4个△,4=22;
第3个图形有9个△,9=32;
……
第n个图形有n2个△;
据此找到规律并解答。
【详解】第4个图形有△的个数:42=16(个)
第n个图形有n2个△。
【点睛】通过数与形的结合,从已知的图形或数据中找到规律,并按规律解题。
14.(1)32
(2)⑩
【分析】第①幅图中☆的颗数表示成;第②幅图中☆的颗数表示成2+4+2=2×4=2×22;第③幅图中☆的颗数表示成2+4+6+4+2=2×9=2×32;……;由此可得。第④幅图中☆的颗数是2×42=32(颗);当有200颗☆时,200÷2=100(颗),100=10×10,故第⑩幅图中有200颗☆。
【详解】(1)2×42=32(颗)
(2)200÷2=100(颗),100=10×10
【点睛】本题主要考查学生的推理能力,关键要发现其中的规律。
15.21根;(2n+1)根
【分析】根据图示发现:摆1个三角形需要小棒:(1+2)根;摆2个三角形需要小棒:(1+2+2)根;摆3个三角形需要小棒:(1+2+2+2)根;依次类推……摆n个三角形需要小棒:(2×n+1)根。据此解答。
【详解】摆n个三角形需要小棒:2×n+1=(2n+1)根
当n=10时,
2×10+1
=20+1
=21(根)
答:摆10个三角形用21根小棒;摆n个三角形用(2n+1)根小棒。
【点睛】本题主要考查数与形结合的规律,关键根据图示发现这组图形的规律,并运用规律做题。
16.鱼宫
【分析】观察表格可知,第一排是按照水、煮、鱼 3个一组循环排列的;第二排是按照宫、保、鸡、丁 4个一组循环排列的,用45分别除以3和4,余数是几就从左边数几即可。
【详解】45÷3=15(组)
45÷4=11(组) 1(个)
答:第45组上面的字是鱼,下面的字是宫。
【点睛】本题考查循环数列,明确上、下几个字为一组是解题的关键。
17.(1)27颗(2)100个
【分析】第1图形有黑色棋子的颗数:6=1×3+3;
第2图形有黑色棋子的颗数:9=2×3+3;
第3图形有黑色棋子的颗数:12=3×3+3;
第4图形有黑色棋子的颗数:15=4×3+3;
……
第n图形有黑色棋子的颗数:n×3+3。
【详解】(1)8×3+3
=24+3
=27(颗)
答:第8个图形中有27颗黑色棋子。
(2)(303-3)÷3
=300÷3
=100(个)
答:第100个图形中有303颗黑色棋子。
【点睛】解题关键是通过归纳与总结,得到其中的规律,再灵活运用规律解答。
18.(1)见详解
(2)45厘米
(3)S=1+4a;
(4)19个
【分析】(1)根据题干可知,1个圆环的长度是5厘米,以后每增加一个圆环,就增加5-0.5×2=4厘米,由此可以完成表格,
(2)观察上表格可得:当有n个圆环,拉紧后的总长度就是:1+4n厘米,由此进行解答;
(3)依据上面规律,代入数据即可得出用字母a、S表示的关系式;
(4)设有n个圆环扣成的,由上面得出的关系式即可得出一个方程,解方程即可。
【详解】(1)1个圆环的长度是5厘米,以后每增加一个圆环,就增加5-0.5×2=4厘米,由此可以完成表格:
圆环个数 1 2 3 4 5 6 ……
拉紧后的长度/cm 5 9 13 17 21 25 ……
(2)观察上表格可得:当有n个圆环,拉紧后的总长度就是:1+4n厘米,
所以,当n=11时,总长度为:
1+11×4
=1+44
=45(厘米)
答:11个圆环拉紧后的长度是45厘米。
(3)设圆环的个数为a,拉紧后的总长度为S,则可得圆环与拉紧后的总长度的关系式:
S=0.5×2+(5-0.5×2)a
=1+4a
答:关系式为:S==1+4a
(4)解:设圆环的个数为x,根据上面关系式可得:
1+4x=77
4x=76
X=19
答:是由19个圆环扣成的。
【点睛】此题考查是的找规律,正确找出规律并用规律解决问题是解题关键。
19.(1)4n个
(2)50个
【分析】第1个图形中有●的个数:4个,4=1×4;
第2个图形中有●的个数:8个,8=2×4;
第3个图形中有●的个数:12个,12=3×4;
……
第n个图形中有●的个数:4n个。
【详解】(1)4×n=4n(个)
答:第n个图形需要4n个●。
(2)200÷4=50(个)
答:摆第50个图形需要用200个●。
【点睛】本题是找规律的题型,从已知的图形或数据中找到规律,并按规律解题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
