3.4 波的干涉 (同步练习)2023-2024学年高二上学期物理人教版(2019)选择性必修第一册(含解析)
文档属性
| 名称 | 3.4 波的干涉 (同步练习)2023-2024学年高二上学期物理人教版(2019)选择性必修第一册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 343.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-12-28 15:41:16 | ||
图片预览


文档简介
3.4 波的干涉 同步练习
选择题
1.蝉是利用了a发出声音,某同学围绕蝉歇息的树干走了一圈,听到忽高忽低的蝉鸣声,这是由于声波的b现象,请选择a、b组合正确的是( )
A.蝉的嘴 干涉 B.蝉的翅膀 干涉
C.蝉的翅膀 共振 D.蝉的嘴 共振
2、利用发波水槽得到的水面波形如图甲、乙所示,则( )
A.图甲、乙均显示了波的干涉现象
B.图甲、乙均显示了波的衍射现象
C.图甲显示了波的干涉现象,图乙显示了波的衍射现象
D.图甲显示了波的衍射现象,图乙显示了波的干涉现象
3、两列沿相反方向传播、振幅和波长都相同的半波(如图甲),在相遇的某一时刻(如图乙)两列波“消失”,此时图中a、b质点的振动方向是( )
A.a向上,b向下 B.a向下,b向上
C.a、b都静止 D.a、b都向上
4、如图所示是水波干涉示意图,、是两波源,、、三点在一条直线上,两波源频率相同,振幅相等,则下列说法正确的是( )
A.处质点一会儿在波峰,一会儿在波谷
B.处质点一直在波谷
C.处质点一会儿在波峰,一会儿在波谷
D.处质点一直在平衡位置
5.主动降噪耳机能够起到降低噪声的作用。耳机内设有麦克风,用来收集周围环境中的噪声信号,在此基础上,耳机的处理器能够预测下一时刻噪声的情况,并产生相应的抵消声波。为达到良好的降噪效果,抵消声波与噪声相比( )
A.振幅相同、频率相同、相位相同 B.振幅相同、频率相同、相位相反
C.振幅较大、频率较大、相位相同 D.振幅较大、频率较小、相位相反
6、如图,S为上下振动的振源,其频率为,所产生的横波向左右传播,波速为,已知和两点与振源相距分别为,,和已经振动起来,当S通过平衡位置向上运动时( )
A.在波峰,在波谷 B.和都在波谷
C.和都在波峰 D.通过平衡位置向上振动,通过平衡位置向下振动
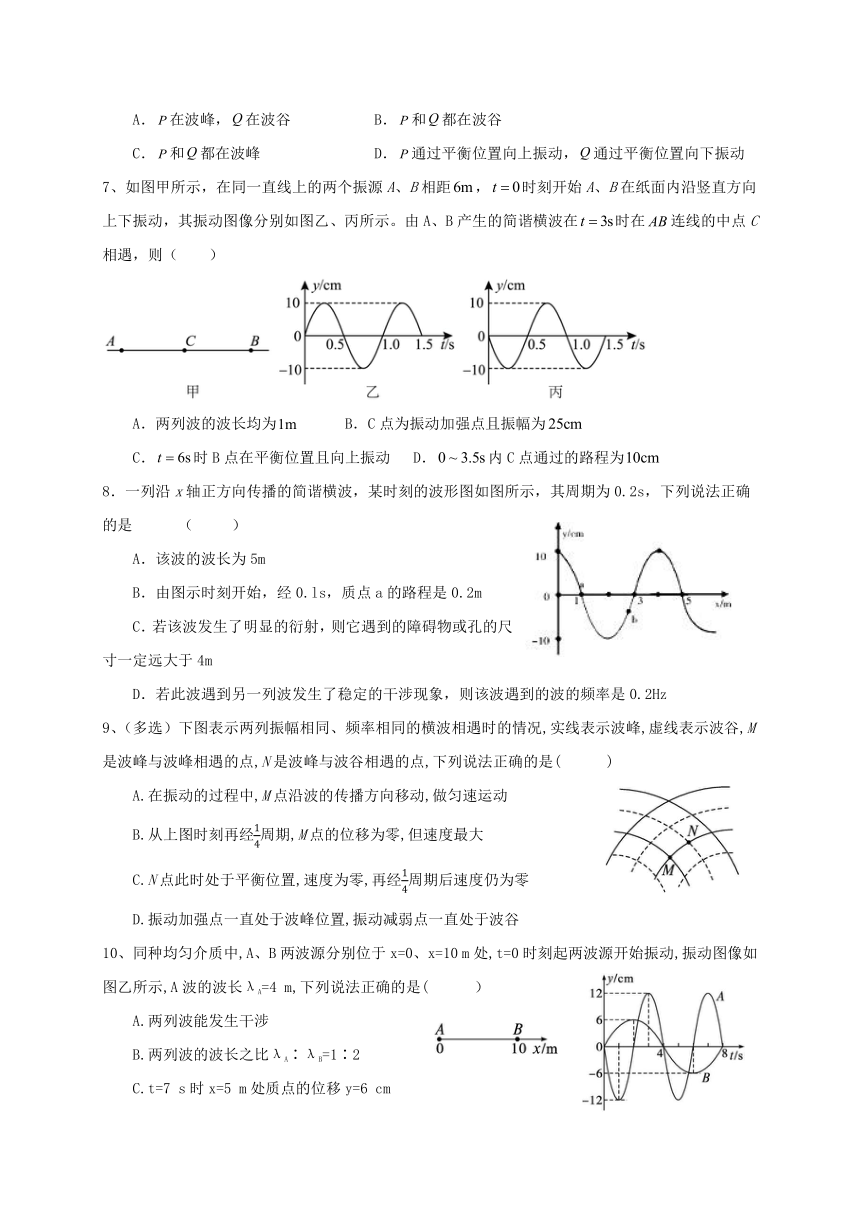
7、如图甲所示,在同一直线上的两个振源A、B相距,时刻开始A、B在纸面内沿竖直方向上下振动,其振动图像分别如图乙、丙所示。由A、B产生的简谐横波在时在连线的中点C相遇,则( )
A.两列波的波长均为 B.C点为振动加强点且振幅为
C.时B点在平衡位置且向上振动 D.内C点通过的路程为
8.一列沿x轴正方向传播的简谐横波,某时刻的波形图如图所示,其周期为0.2s,下列说法正确的是 ( )
A.该波的波长为5m
B.由图示时刻开始,经0.ls,质点a的路程是0.2m
C.若该波发生了明显的衍射,则它遇到的障碍物或孔的尺寸一定远大于4m
D.若此波遇到另一列波发生了稳定的干涉现象,则该波遇到的波的频率是0.2Hz
9、(多选)下图表示两列振幅相同、频率相同的横波相遇时的情况,实线表示波峰,虚线表示波谷,M是波峰与波峰相遇的点,N是波峰与波谷相遇的点,下列说法正确的是( )
A.在振动的过程中,M点沿波的传播方向移动,做匀速运动
B.从上图时刻再经周期,M点的位移为零,但速度最大
C.N点此时处于平衡位置,速度为零,再经周期后速度仍为零
D.振动加强点一直处于波峰位置,振动减弱点一直处于波谷
10、同种均匀介质中,A、B两波源分别位于x=0、x=10 m处,t=0时刻起两波源开始振动,振动图像如图乙所示,A波的波长λA=4 m,下列说法正确的是( )
A.两列波能发生干涉
B.两列波的波长之比λA∶λB=1∶2
C.t=7 s时x=5 m处质点的位移y=6 cm
D.t=7.5 s时第一次有质点位于|y|=18 cm处
二、非选择题
11、填空题
(1).如图甲所示,为一列简谐横波在t=0.1s时刻的波形图,图乙为质点P的振动图像。有此可知该列简谐波沿x轴___________方向传播,波速为___________m/s;若该波与另一列频率为5Hz、波源在x=0m处的沿x轴正方向传播的简谐横波相遇,___________ (填“能够”或“不能”)产生稳定的干涉图样。
(2).如图所示,实线表示两个相干波源S1、S2发出的波的波峰位置,b点在两个波源连线的中垂线上,则图中的___________点为振动加强的位置,图中的_______________点为振动减弱的位置.(选填“a”、“b”、“c”)
12、一根长20 m的软绳拉直后放置在光滑水平地板上,两人在绳两端P、Q沿y轴方向不断有节奏地抖动,形成两列振幅分别为10 cm、20 cm的相向传播的机械波。以绳中点为坐标原点,以绳上各质点的平衡位置为x轴建立坐标系,t=0时刻的波形如图所示。已知P端的波波速为2 m/s。
(1)求两列波的频率。
(2)两列波叠加稳定时,求两波源间(不含波源)振动加强的点共有几个,并写出其位置坐标。
答 卷
班次: 姓名: 考号:
题号 1 2 3 4 5 6 7 8 9 10
答案
二、非选择题
11、(1)___________;___________;___________
(2)___________; ___________
12、
答案和解析
1.【答案】B 【解析】蝉是依靠一双翅膀的振动发声,两翅膀的振动频率、振幅相同,形成相干波源,在周围出现振动加强与减弱的区域。选项B正确。
2、【答案】D 【解析】由波的干涉和衍射概念知,题图甲是一列波的传播,显示了波的衍射现象,题图乙是两列波的传播,显示了波的干涉现象。
3、【答案】B 【解析】a、b质点的振动方向是两列波振动的叠加,根据波的传播方向和波形,可判知质点的振动方向,选项B正确。
4.【答案】A 【详解】ABD.A、B、D三点都在振动加强区,三处质点均做简谐运动,质点一会儿在波峰,一会儿在波谷,选项A正确,B、D错误;
C.点C是振动减弱点,又因两波振幅相等,故C处质点一直在平衡位置不动,选项C错误.
5、【答案】B 【详解】抵消声波与噪声能够实现干涉相消,需要二者的振幅、频率相同,相位相反,叠加后相互抵消。故选B。
6、【答案】A 【详解】 由 得,波长
则 P、S相当于相距时的关系
、相当于相距时的关系,结合如图波形可知,当S通过平衡位置向上运动,此时刻质点在波峰,在波谷,故A正确,BCD错误。 故选A。
7、【答案】A 【详解】 A. 根据乙丙图像可知,A、B的振动周期为,A、B产生的简谐横波在时在连线的中点C相遇,可知两列波各经过3个周期,A、B相距,可知两列波的波长均为,故A正确; B.两列波同时传到C点,且振动方向相反,因此C点为振动减弱点且振幅为 故B错误;
C.根据图像A波传到B位置需要6s向上振动,时B波经过六个周期,向下振动,AB两个波源的周期相同,振幅相同,则时B点在平衡位置没有振动,故C错误;
D.时两列波同时传到C点,且振动方向相反,因此C点为振动减弱点且振幅为 则内C点通过的路程为零,故D错误。 故选A。
8、【答案】B 【详解】 由波形图可知,该波的波长为λ=4m,选项A错误;因T=0.2s,则0.1s=0.5T,则由图示时刻开始,经0.ls,质点a的路程是2A=20cm=0.2m,选项B正确;因该波的波长为4m,则若该波发生了明显的衍射,则它遇到的障碍物或孔的尺寸一定远小于4m,选项C错误;波的频率为f=1/T=5Hz,则若此波遇到另一列波发生了稳定的干涉现象,则该波遇到的波的频率是5Hz,选项D错误;故选B.
9、【答案】BC 【解析】M点只振动不移动,选项A错误;M点此时位移为正向最大,再经周期,运动到平衡位置,位移为零,速度最大,选项B正确;N是波峰与波谷相遇的点,两列波振幅相同、频率相同,所以N点的振幅始终等于零,始终静止,选项C正确;振动加强点也在平衡位置两侧振动,振幅最大,振动减弱点的振幅最小,选项D错误。
10、【答案】BCD 【解析】两个波在同种均匀介质中,波速相等,两列波的波长不相等,所以两列波的频率不相等,两列波不能发生干涉,故选项A错误;由振动图像可知,A波的周期TA=4 s,B波的周期TB=8 s,两列波的波长之比,故选项B正确;波在介质中传播速度v==1 m/s,t0=5 s时两列波同时传播到x=5 m处质点,t=7 s时A波单独传播到该点时产生的位移为0,B波单独传播到该点时产生的位移为6 cm,所以t=7 s时x=5 m处质点的位移y=6 cm,故选项C正确;t0=5 s时两列波相遇,A波单独传播到相遇点时向下振动,B波单独传播到该点时向上振动,此时,两列波最近的两波峰相距5 m,两列波最近的波谷相距7 m,所以第一次有质点位于|y|=18 cm处出现在两列波的波峰相遇,所用时间Δt= s=2.5 s,第一次有质点位于|y|=18 cm处的时间t=t0+Δt=7.5 s,所以t=7.5 s时第一次有质点位于|y|=18 cm处,故选项D正确。
11、(1)【答案】 负 20 能够【详解】在图乙中,t=0.1s时刻P正向下振动,在图甲中,根据波形平移法可知波正在向x轴负方向传播; 该波的波长和周期分别为λ=4m,T=0.2s,所以波速 ,当两列波的频率相同时,相遇时能产生稳定的干涉,可知若该波与另一列频率为5Hz、波源在x=0m处的沿x轴正方向传播的简谐横波相遇,能够产生稳定的干涉图样。
(2)【答案】bc a【详解】 根据图像可知,c处是波谷与波谷相遇的位置,所以c点是加强点;b点正好在加强点构成的连线上,即处在加强区内,所以b点也是加强点;a处是波峰与波谷相遇的位置,所以a点是减弱点.
12、【答案】(1)0.5 Hz (2)9个 x=0,x=2 m,x=-2 m,x=4 m,x=-4 m,x=6 m,x=-6 m,x=8 m,x=-8 m
【解析】(1)两列波的波速均为v=2 m/s,由题图可知,绳端P形成的波波长为4 m,绳端Q形成的波波长也为4 m,由波速公式v=λf可知,两列波的频率均为f==0.5 Hz。
(2)叠加稳定时两波源间与两波源路程差等于nλ(n=0,1,2,…)的各点振动加强,振幅为30 cm,设某点是振动加强点,到两个波源的距离分别为x1和x2,则有x1+x2=20 m,|x1-x2|=nλ(n=0,1,2,…)解得x1=(10±2n) m(n=0,1,2,…)由于0
选择题
1.蝉是利用了a发出声音,某同学围绕蝉歇息的树干走了一圈,听到忽高忽低的蝉鸣声,这是由于声波的b现象,请选择a、b组合正确的是( )
A.蝉的嘴 干涉 B.蝉的翅膀 干涉
C.蝉的翅膀 共振 D.蝉的嘴 共振
2、利用发波水槽得到的水面波形如图甲、乙所示,则( )
A.图甲、乙均显示了波的干涉现象
B.图甲、乙均显示了波的衍射现象
C.图甲显示了波的干涉现象,图乙显示了波的衍射现象
D.图甲显示了波的衍射现象,图乙显示了波的干涉现象
3、两列沿相反方向传播、振幅和波长都相同的半波(如图甲),在相遇的某一时刻(如图乙)两列波“消失”,此时图中a、b质点的振动方向是( )
A.a向上,b向下 B.a向下,b向上
C.a、b都静止 D.a、b都向上
4、如图所示是水波干涉示意图,、是两波源,、、三点在一条直线上,两波源频率相同,振幅相等,则下列说法正确的是( )
A.处质点一会儿在波峰,一会儿在波谷
B.处质点一直在波谷
C.处质点一会儿在波峰,一会儿在波谷
D.处质点一直在平衡位置
5.主动降噪耳机能够起到降低噪声的作用。耳机内设有麦克风,用来收集周围环境中的噪声信号,在此基础上,耳机的处理器能够预测下一时刻噪声的情况,并产生相应的抵消声波。为达到良好的降噪效果,抵消声波与噪声相比( )
A.振幅相同、频率相同、相位相同 B.振幅相同、频率相同、相位相反
C.振幅较大、频率较大、相位相同 D.振幅较大、频率较小、相位相反
6、如图,S为上下振动的振源,其频率为,所产生的横波向左右传播,波速为,已知和两点与振源相距分别为,,和已经振动起来,当S通过平衡位置向上运动时( )
A.在波峰,在波谷 B.和都在波谷
C.和都在波峰 D.通过平衡位置向上振动,通过平衡位置向下振动
7、如图甲所示,在同一直线上的两个振源A、B相距,时刻开始A、B在纸面内沿竖直方向上下振动,其振动图像分别如图乙、丙所示。由A、B产生的简谐横波在时在连线的中点C相遇,则( )
A.两列波的波长均为 B.C点为振动加强点且振幅为
C.时B点在平衡位置且向上振动 D.内C点通过的路程为
8.一列沿x轴正方向传播的简谐横波,某时刻的波形图如图所示,其周期为0.2s,下列说法正确的是 ( )
A.该波的波长为5m
B.由图示时刻开始,经0.ls,质点a的路程是0.2m
C.若该波发生了明显的衍射,则它遇到的障碍物或孔的尺寸一定远大于4m
D.若此波遇到另一列波发生了稳定的干涉现象,则该波遇到的波的频率是0.2Hz
9、(多选)下图表示两列振幅相同、频率相同的横波相遇时的情况,实线表示波峰,虚线表示波谷,M是波峰与波峰相遇的点,N是波峰与波谷相遇的点,下列说法正确的是( )
A.在振动的过程中,M点沿波的传播方向移动,做匀速运动
B.从上图时刻再经周期,M点的位移为零,但速度最大
C.N点此时处于平衡位置,速度为零,再经周期后速度仍为零
D.振动加强点一直处于波峰位置,振动减弱点一直处于波谷
10、同种均匀介质中,A、B两波源分别位于x=0、x=10 m处,t=0时刻起两波源开始振动,振动图像如图乙所示,A波的波长λA=4 m,下列说法正确的是( )
A.两列波能发生干涉
B.两列波的波长之比λA∶λB=1∶2
C.t=7 s时x=5 m处质点的位移y=6 cm
D.t=7.5 s时第一次有质点位于|y|=18 cm处
二、非选择题
11、填空题
(1).如图甲所示,为一列简谐横波在t=0.1s时刻的波形图,图乙为质点P的振动图像。有此可知该列简谐波沿x轴___________方向传播,波速为___________m/s;若该波与另一列频率为5Hz、波源在x=0m处的沿x轴正方向传播的简谐横波相遇,___________ (填“能够”或“不能”)产生稳定的干涉图样。
(2).如图所示,实线表示两个相干波源S1、S2发出的波的波峰位置,b点在两个波源连线的中垂线上,则图中的___________点为振动加强的位置,图中的_______________点为振动减弱的位置.(选填“a”、“b”、“c”)
12、一根长20 m的软绳拉直后放置在光滑水平地板上,两人在绳两端P、Q沿y轴方向不断有节奏地抖动,形成两列振幅分别为10 cm、20 cm的相向传播的机械波。以绳中点为坐标原点,以绳上各质点的平衡位置为x轴建立坐标系,t=0时刻的波形如图所示。已知P端的波波速为2 m/s。
(1)求两列波的频率。
(2)两列波叠加稳定时,求两波源间(不含波源)振动加强的点共有几个,并写出其位置坐标。
答 卷
班次: 姓名: 考号:
题号 1 2 3 4 5 6 7 8 9 10
答案
二、非选择题
11、(1)___________;___________;___________
(2)___________; ___________
12、
答案和解析
1.【答案】B 【解析】蝉是依靠一双翅膀的振动发声,两翅膀的振动频率、振幅相同,形成相干波源,在周围出现振动加强与减弱的区域。选项B正确。
2、【答案】D 【解析】由波的干涉和衍射概念知,题图甲是一列波的传播,显示了波的衍射现象,题图乙是两列波的传播,显示了波的干涉现象。
3、【答案】B 【解析】a、b质点的振动方向是两列波振动的叠加,根据波的传播方向和波形,可判知质点的振动方向,选项B正确。
4.【答案】A 【详解】ABD.A、B、D三点都在振动加强区,三处质点均做简谐运动,质点一会儿在波峰,一会儿在波谷,选项A正确,B、D错误;
C.点C是振动减弱点,又因两波振幅相等,故C处质点一直在平衡位置不动,选项C错误.
5、【答案】B 【详解】抵消声波与噪声能够实现干涉相消,需要二者的振幅、频率相同,相位相反,叠加后相互抵消。故选B。
6、【答案】A 【详解】 由 得,波长
则 P、S相当于相距时的关系
、相当于相距时的关系,结合如图波形可知,当S通过平衡位置向上运动,此时刻质点在波峰,在波谷,故A正确,BCD错误。 故选A。
7、【答案】A 【详解】 A. 根据乙丙图像可知,A、B的振动周期为,A、B产生的简谐横波在时在连线的中点C相遇,可知两列波各经过3个周期,A、B相距,可知两列波的波长均为,故A正确; B.两列波同时传到C点,且振动方向相反,因此C点为振动减弱点且振幅为 故B错误;
C.根据图像A波传到B位置需要6s向上振动,时B波经过六个周期,向下振动,AB两个波源的周期相同,振幅相同,则时B点在平衡位置没有振动,故C错误;
D.时两列波同时传到C点,且振动方向相反,因此C点为振动减弱点且振幅为 则内C点通过的路程为零,故D错误。 故选A。
8、【答案】B 【详解】 由波形图可知,该波的波长为λ=4m,选项A错误;因T=0.2s,则0.1s=0.5T,则由图示时刻开始,经0.ls,质点a的路程是2A=20cm=0.2m,选项B正确;因该波的波长为4m,则若该波发生了明显的衍射,则它遇到的障碍物或孔的尺寸一定远小于4m,选项C错误;波的频率为f=1/T=5Hz,则若此波遇到另一列波发生了稳定的干涉现象,则该波遇到的波的频率是5Hz,选项D错误;故选B.
9、【答案】BC 【解析】M点只振动不移动,选项A错误;M点此时位移为正向最大,再经周期,运动到平衡位置,位移为零,速度最大,选项B正确;N是波峰与波谷相遇的点,两列波振幅相同、频率相同,所以N点的振幅始终等于零,始终静止,选项C正确;振动加强点也在平衡位置两侧振动,振幅最大,振动减弱点的振幅最小,选项D错误。
10、【答案】BCD 【解析】两个波在同种均匀介质中,波速相等,两列波的波长不相等,所以两列波的频率不相等,两列波不能发生干涉,故选项A错误;由振动图像可知,A波的周期TA=4 s,B波的周期TB=8 s,两列波的波长之比,故选项B正确;波在介质中传播速度v==1 m/s,t0=5 s时两列波同时传播到x=5 m处质点,t=7 s时A波单独传播到该点时产生的位移为0,B波单独传播到该点时产生的位移为6 cm,所以t=7 s时x=5 m处质点的位移y=6 cm,故选项C正确;t0=5 s时两列波相遇,A波单独传播到相遇点时向下振动,B波单独传播到该点时向上振动,此时,两列波最近的两波峰相距5 m,两列波最近的波谷相距7 m,所以第一次有质点位于|y|=18 cm处出现在两列波的波峰相遇,所用时间Δt= s=2.5 s,第一次有质点位于|y|=18 cm处的时间t=t0+Δt=7.5 s,所以t=7.5 s时第一次有质点位于|y|=18 cm处,故选项D正确。
11、(1)【答案】 负 20 能够【详解】在图乙中,t=0.1s时刻P正向下振动,在图甲中,根据波形平移法可知波正在向x轴负方向传播; 该波的波长和周期分别为λ=4m,T=0.2s,所以波速 ,当两列波的频率相同时,相遇时能产生稳定的干涉,可知若该波与另一列频率为5Hz、波源在x=0m处的沿x轴正方向传播的简谐横波相遇,能够产生稳定的干涉图样。
(2)【答案】bc a【详解】 根据图像可知,c处是波谷与波谷相遇的位置,所以c点是加强点;b点正好在加强点构成的连线上,即处在加强区内,所以b点也是加强点;a处是波峰与波谷相遇的位置,所以a点是减弱点.
12、【答案】(1)0.5 Hz (2)9个 x=0,x=2 m,x=-2 m,x=4 m,x=-4 m,x=6 m,x=-6 m,x=8 m,x=-8 m
【解析】(1)两列波的波速均为v=2 m/s,由题图可知,绳端P形成的波波长为4 m,绳端Q形成的波波长也为4 m,由波速公式v=λf可知,两列波的频率均为f==0.5 Hz。
(2)叠加稳定时两波源间与两波源路程差等于nλ(n=0,1,2,…)的各点振动加强,振幅为30 cm,设某点是振动加强点,到两个波源的距离分别为x1和x2,则有x1+x2=20 m,|x1-x2|=nλ(n=0,1,2,…)解得x1=(10±2n) m(n=0,1,2,…)由于0
