期末模拟测试卷-数学五年级上册青岛版(含答案)
文档属性
| 名称 | 期末模拟测试卷-数学五年级上册青岛版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-28 20:08:03 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末模拟测试卷-数学五年级上册青岛版
一、选择题
1.下列各式中,积最大的是( )。
A.1.6×3.05 B.160×0.305 C.1.6×0.305
2.循环小数0.3296296…中,小数点后面第99位上的数字是( )。
A.3 B.2 C.9 D.6
3.已知a=2×3×5,那么a的因数一共有( )个。
A.6 B.7 C.8
4.已知□+□+〇=19,□+〇=12,那么□和〇各是( )。
A.8和4 B.7和5 C.6和7
5.下面不适合用折线统计图表示是( )。
A.第27届—第32届夏季奥运会中国获得金牌数的变化情况。
B.2015年—2020年德州市接待游客人数的变化情况。
C.2020年山东省月降水量的变化情况。
D.2021年新冠肺炎全国各地感染人数。
6.如图,两个长方形完全相同,则阴影部分的面积( )。
A.甲>乙 B.甲<乙 C.甲=乙
二、填空题
7.我国的高铁向世界展示了“中国速度”。普通火车的速度是每小时120千米,高铁的速度可以达到普通火车的2.92倍,高铁的速度是( )千米/时。(得数保留整数)
8.在括号里填上“>”“<”或者“=”。
6.27×1.09( )6.27 4.2×0.7( )0.07×42 0.91÷0.7( )0.91
4.7×0.6( )4.7 9.63×1( )9.63÷1 11.4÷1.06( )11.4
9.选出两张不同的数字卡片,写出所有符合要求的两位数。
(1)组成的数是奇数:( );
(2)组成的数是5的倍数:( );
(3)组成的数既是2的倍数,又是5的倍数:( );
(4)组成的数既是奇数,又是5的倍数:( )。
10.
根据上图列方程( )。
11.一个三角形的底是25米,高是20米,面积是( )平方米,与这个三角形等底等高的平行四边形的面积是( )平方米。
12.一个梯形的面积是84平方米,高是4米,它的下底比上底多3米,这个梯形的上底是( )米.
三、判断题
13.在2.6×1.5+3.4×1.5=(2.6+3.4)×1.5中,运用了乘法结合律。( )
14.14.3535353535是循环小数。( )
15.方程与的解相同,则a等于18.2。( )
16.统计某地区2019年月平均气温变化情况用折线统计图比较好。( )
17.把一个长方形框架拉成一个平行四边形后,它的周长变了,面积没变。( )
四、计算题
18.直接写得数。
6.7+2.5= 3.4×8= 6.7÷2= 4.8÷0.06= 12.5×0.8+0.2=
8.5-5.8= 2.5×0.4= 5.2÷4= 3.5×6= 0.4×0.2÷0.4×0.2=
19.竖式计算。(带△的得数保留两位小数。)
①0.35×0.18= ②△8.05÷3.7≈
20.计算下列各题,能简算的要简算。
7.86×1.01-7.86 8.4÷0.21÷0.4 99×0.45+0.45
0.96÷[0.5×(6-2.8)] 5.6×102 3.2×2.4+32×0.76
21.解方程。(带☆的要检验)
☆
22.求下面组合图形的面积。(单位:厘米)
五、解答题
23.李老师打算买3盒钢笔奖励给表现优异的学生,一盒钢笔有12支,每支6.5元,买这些钢笔一共需要多少钱?
24.一辆汽车0.8小时行驶15.2千米,照这样计算,行驶228千米需要多少小时?
25.甲、乙两市相距855千米。一辆慢车从甲市开往乙市,每小时行60千米,3小时后,一辆快车从乙市开往甲市,每小时行75千米。快车开出几小时后两车相遇?(列方程解答)
26.甲、乙两地相距560千米,一辆客车和一辆货车同时从甲、乙两地相向而行,4小时后两车相遇。客车每小时行73.5千米,货车每小时行多少千米?
27.爷爷家有一块三角形的小麦地,底32米、高15米,今年一共收小麦134.4千克.平均每平方米收小麦多少千克?
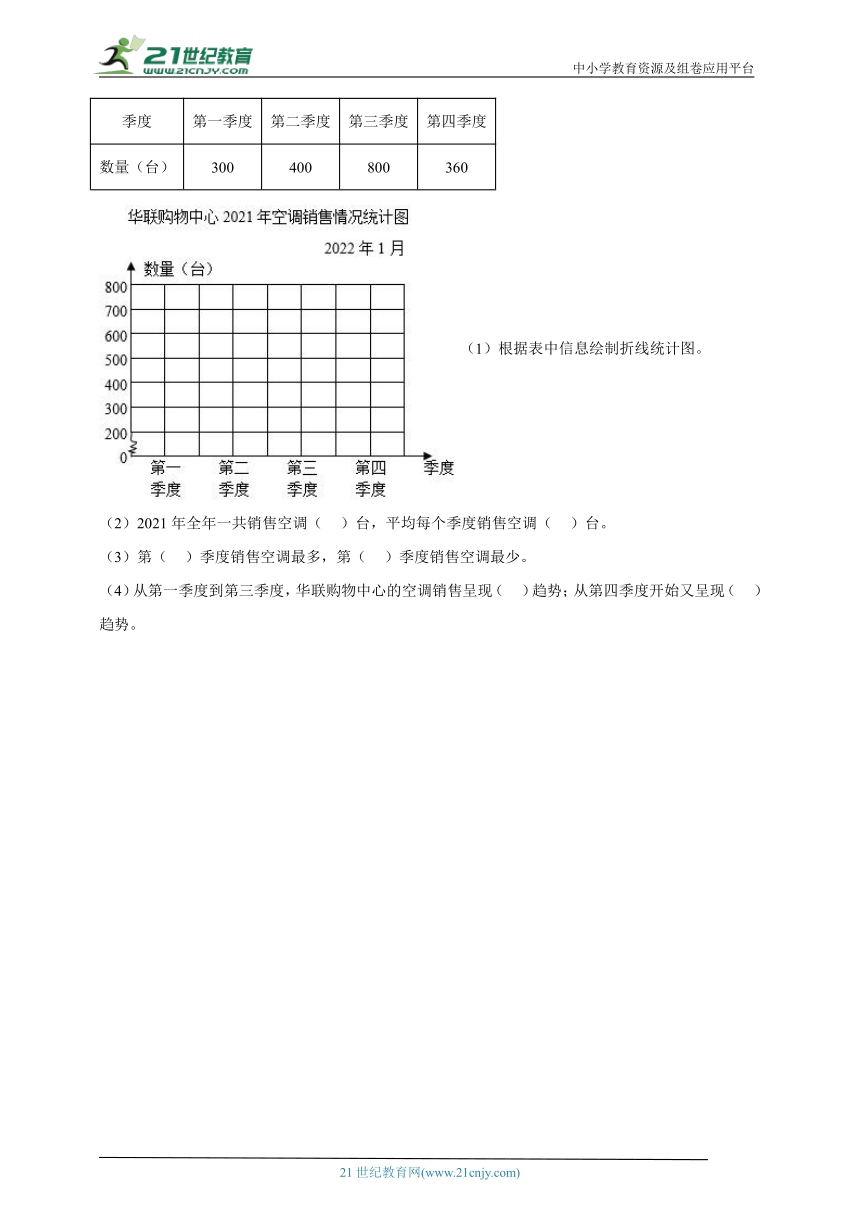
28.华联购物中心2021年空调销售情况统计。
季度 第一季度 第二季度 第三季度 第四季度
数量(台) 300 400 800 360
(1)根据表中信息绘制折线统计图。
(2)2021年全年一共销售空调( )台,平均每个季度销售空调( )台。
(3)第( )季度销售空调最多,第( )季度销售空调最少。
(4)从第一季度到第三季度,华联购物中心的空调销售呈现( )趋势;从第四季度开始又呈现( )趋势。
参考答案:
1.B
【分析】小数乘法法则:
(1)按整数乘法法则先算出积。
(2)看因数中一共有几位小数,就从积的右边起,数出几位点上小数点。
据此计算出每个选项的具体数值,后比较大小即可。
【详解】由分析可得:
A.1.6×3.05=4.88
B.160×0.305=48.8
C.1.6×0.305=0.488
48.8>4.88>0.488
所以,积最大的是160×0.305。
故答案为:B
2.C
【分析】循环小数0.3296296…中,循环节是296,每3个数字一循环,因为小数点后面第一位是3,不参与循环,所以求小数点后面第99位上的数字,就是求(99-1)里面有几个3,用除法计算,然后根据余数的情况,判断出小数点后面第99位上的数字。
【详解】99-1=98
98÷3=32……2
余数是2表示是一个循环里的第2个数,即9;
所以小数点后面第99位上的数字是9。
故答案为:C
3.C
【分析】先根据a=2×3×5,求出a的值,再根据求一个数因数的方法,求出a的所有因数,即可解答。
【详解】a=2×3×5
a=6×5
a=30
30的因数有:1,2,3,5,6,10,15,30一共8个。
已知a=2×3×5,那么a的因数一共有8个。
故答案为:C
【点睛】求出a的值是解答本题的关键。
4.B
【分析】根据题意可知用19减去12即可求出□是几,用12减去□,即可求出〇是几,据此列式解答即可。
【详解】19-12=7
12-7=5
则□和〇各是7和5。
故答案为:B
5.D
【分析】根据折线统计图的特点可知:折线统计图不仅能够看出数量的多少,而且还能清楚地看出数量增减变化的情况。据此判断。
【详解】A. 第27届—第32届夏季奥运会中国获得金牌数的变化情况。有金牌数量的增减变化,可用折线统计图表示。
B. 2015年—2020年德州市接待游客人数的变化情况。有游客人数的增减变化,可用折线统计图表示。
C. 2020年山东省月降水量的变化情况。有月降水量的增减变化,可用折线统计图表示。
D. 2021年新冠肺炎全国各地感染人数。可用条形统计图直观表示出全国各地感染人数。
故答案为:D
【点睛】掌握折线统计图的特点是解答此类题的关键。
6.C
【分析】两个长方形完全相同,从图中可知,甲三角形的底等于长方形的长,高等于长方形的宽;乙三角形的底等于长方形的宽,高等于长方形的长;
根据长方形的面积=长×宽,三角形的面积=底×高÷2,可知甲、乙两个三角形的面积都等于长方形面积的一半,据此解答。
【详解】甲三角形的面积=长×宽÷2
乙三角形的面积=宽×长÷2
甲三角形的面积=乙三角形的面积=长方形面积的一半;
所以阴影部分的面积甲=乙。
故答案为:C
【点睛】找出两个阴影三角形的底、高与长方形的长、宽的关系是解题的关键。
7.350
【分析】根据小数乘法的意义,用120×2.92即可求出高铁的速度;保留两位整数就是精确到个位,要看十分位上的数字是几,然后根据四舍五入的方法取近似值。
【详解】120×2.92≈350(千米/时)
高铁的速度是350千米/时。
8. > = > < = <
【分析】(1)一个数(0除外)乘大于1的数,积比原来的数大;
(2)观察4.2×0.7和0.07×42,发现因数的数字都相同,只是小数位不同,根据“积的小数位数等于所有因数的小数位数之和”得出4.2×0.7的积和0.07×42的积都是两位小数,所以它们的积相等;
(3)一个数(0除外)除以小于1的数,商比原来的数大;
(4)一个数(0除外)乘小于1的数,积比原来的数小;
(5)一个数(0除外)乘1,积等于原来的数;
一个数(0除外)除以1,商等于原来的数;
(6)一个数(0除外)除以大于1的数,商比原来的数小。
【详解】(1)1.09>1,所以6.27×1.09>6.27;
(2)4.2×0.7=0.07×42
(3)0.7<1,所以0.91÷0.7>0.91;
(4)0.6<1,所以4.7×0.6<4.7;
(5)9.63×1=9.63÷1
(6)1.06>1,所以 11.4÷1.06<11.4。
9.(1)35、53、83、85
(2)35、30、50、85、80
(3)30、50、80
(4)35、85
【分析】奇数的特征:个位上是1、3、5、7、9的数;5的倍数特征:个位上是0或5的数;2的倍数特征:个位上是0、2、4、6、8的数;既是2的倍数,又是5的倍数:个位上是0的数;组成的数既是奇数,又是5的倍数:个位上是5的数,据此解答即可。
【详解】(1)组成的数是奇数:35、53、83、85;
(2)组成的数是5的倍数:35、30、50、85、80;
(3)组成的数既是2的倍数,又是5的倍数:30、50、80;
(4)组成的数既是奇数,又是5的倍数:35、85。
【点睛】本题考查2和5的倍数、奇数,解答本题的关键是掌握这些知识点。
10.
【分析】本子的价钱是未知数,根据本子的价钱和笔的价钱总共是20元列方程。
【详解】
【点睛】方程必须满足两个基本要素,必须是等式,必须含有未知数。
11. 250 500
【分析】已知三角形的底和高,根据三角形的面积=底×高÷2,代入数据计算即可求出这个三角形的面积。
根据三角形的面积=底×高÷2,平行四边形的面积=底×高,可知等底等高的平行四边形的面积是三角形面积的2倍,据此解答。
【详解】25×20÷2
=500÷2
=250(平方米)
250×2=500(平方米)
三角形的面积是250平方米,与这个三角形等底等高的平行四边形的面积是500平方米。
【点睛】本题考查三角形、平行四边形面积公式的运用,掌握等底等高的三角形和平行四边形面积之间的关系是解题的关键。
12.19.5
【解析】略
13.×
【分析】加法交换律:两个数相加,交换加数的位置,和不变。
乘法交换律:两个数相乘,交换两个因数的位置,积不变。
乘法结合律:三个数相乘,先乘前两个数,或者先乘后两个数,积不变。
乘法分配律:两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。
【详解】分析可知,在2.6×1.5+3.4×1.5=(2.6+3.4)×1.5中,运用了乘法分配律。
故答案为:×
14.×
【分析】小数分为有限小数和无限小数,小数部分的数位是有限的小数,叫做有限小数,小数部分的数位是无限的小数,叫做无限小数;循环小数是无限小数,再根据循环小数的意义以及特征:一个数的小数部分,从某一位起,一个数字或几个数字依次不断重复出现,这样的小数叫做循环小数,据此解答。
【详解】根据分析可知,14.3535353535是有限小数,不是循环小数。
原题干说法错误。
故答案为:×
15.√
【分析】根据等式的性质2,将左右两边同时乘8,即可求出x的值,因为方程与的解相同,则把x的值代入中,再根据等式的性质1和2进行解答即可。
【详解】
解:
解:
a等于18.2,原题说法正确。
故答案为:√
【点睛】本题考查了解方程的方法,掌握相应的计算方法是解答本题的关键。
16.√
【分析】折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况,由此解答即可。
【详解】因为要统计某地区一年12个月的月平均气温变化情况,所以选用折线统计图比较合适。
故答案为:√
【点睛】掌握折线统计图的特点是解答本题的关键。
17.×
【分析】把一个长方形框架拉成一个平行四边形,长方形的长相当于平行四边形的底,长方形的宽相当于平行四边形底边的邻边,则四条边的总长度不变,比较长方形的宽和平行四边形高的大小关系,确定长方形和平行四边形面积的大小关系即可。
【详解】分析可知,长方形的周长=平行四边形的周长
长方形的长=平行四边形的底,长方形的宽>平行四边形的高
长方形的面积=长×宽,平行四边形的面积=底×高
长×宽>底×高,则长方形的面积>平行四边形的面积
所以,把一个长方形框架拉成一个平行四边形,周长没变,面积变了,原题说法错误。
故答案为:×
【点睛】分析平行四边形的高与长方形宽的大小关系是解答题目的关键。
18.9.2;27.2;3.35;80;10.2
2.7;1;1.3;21;0.04
【解析】略
19.①0.063;②2.18
【分析】小数乘小数的计算方法,先按照整数乘法的计算方法计算,再看因数中共有几位小数,就从积的右边起数出几位点上小数点;
小数除法计算方法:在计算除数是小数的除法时。根据商不变的性质,将除数和被除数同时扩大相同的倍数,转化成除数是整数的除法进行计算;得数保留两位小数,看千分位上的数字是否满5,然后运用“四舍五入”法求得近似数即可。
【详解】① 0.35×0.18=0.063 ②△8.05÷3.7≈2.18
20.0.0786;100;45;
0.6;571.2;32
【分析】(1)运用乘法分配律进行计算即可;
(2)运用除法的性质进行计算即可;
(3)运用乘法分配律进行计算即可;
(4)先算小括号里面的减法,再算中括号里面的乘法,最后算括号外面的除法;
(5)把102拆成100+2,再运用乘法分配律进行计算即可;
(6)根据积不变的规律,把原式化为3.2×2.4+3.2×7.6,再运用乘法分配律进行计算即可。
【详解】7.86×1.01-7.86
=7.86×(1.01-1)
=7.86×0.01
=0.0786
8.4÷0.21÷0.4
=8.4÷(0.21×0.4)
=8.4÷0.084
=100
99×0.45+0.45
=(99+1)×0.45
=100×0.45
=45
0.96÷[0.5×(6-2.8)]
=0.96÷[0.5×3.2]
=0.96÷1.6
=0.6
5.6×102
=5.6×(100+2)
=5.6×100+5.6×2
=560+11.2
=571.2
3.2×2.4+32×0.76
=3.2×2.4+3.2×7.6
=3.2×(2.4+7.6)
=3.2×10
=32
21.;
【分析】根据等式的性质解方程。
(1)方程两边同时加上,求出方程的解;
(2)方程两边同时乘,求出方程的解。
【详解】(1)
解:
(2)
解:
检验:
方程左边
方程右边
所以,是方程的解。
22.696平方厘米
【分析】三角形的面积=底×高÷2,长方形的面积=长×宽,梯形的面积=(上底+下底)×高÷2,整个图形的面积=三角形的面积+长方形的面积+梯形的面积,据此解答。
【详解】8×10÷2+8×70+(8+16)×8÷2
=8×10÷2+8×70+24×8÷2
=40+560+96
=696(平方厘米)
所以,组合图形的面积是696平方厘米。
23.234元
【分析】用每盒钢笔的支数乘盒数,求出一共有多少支钢笔,再根据“单价×数量=总价”,代入数值求出一共需要的钱数即可。
【详解】
(元)
答:买这些钢笔一共需要234元钱。
24.12小时
【分析】根据速度=路程÷时间,代入数值,先求出速度,再根据时间=路程÷速度,代入数值即可求出行驶228千米需要多少小时。
【详解】228÷(15.2÷0.8)
=228÷19
=12(小时)
答:行驶228千米需要12小时。
25.5小时
【分析】由题意可知,根据速度×时间=路程,即用60乘3即可求出慢车3小时可行驶的距离,此时快车和慢车相遇的路程为855-60×3=675千米,设快车开出后x小时两车相遇,再根据等量关系:速度和×相遇时间=相遇的路程,据此列方程解答即可。
【详解】解:设快车开出后x小时两车相遇。
(60+75)x=855-60×3
(60+75)x=855-180
(60+75)x=675
135x=675
135x÷135=675÷135
x=5
答:快车开出5小时后两车相遇。
26.66.5千米
【分析】根据“速度×时间=路程”可得出等量关系:客车的速度×相遇时间+货车的速度×相遇时间=甲、乙两地的距离,据此列出方程,并求解。
【详解】解:设货车每小时行千米。
73.5×4+4=560
294+4=560
294+4-294=560-294
4=266
4÷4=266÷4
=66.5
答:货车每小时行66.5千米。
【点睛】本题考查列方程解决问题,根据速度、时间、路程之间的关系得出等量关系,按等量关系列出方程。
27.0.56千克
【分析】先利用三角形面积公式求出这块地的面积,总产量除以这块地的面积,就是每平方米的小麦产量。
【详解】134.4÷(32×15÷2)
=134.4÷240
=0.56(千克)
答:平均每平方米收小麦0.56千克。
【点睛】此题主要考查三角形的面积公式及“总产量÷总面积=单产量”。
28.(1)见详解;
(2)1860;465;
(3)三;一;
(4)上升;下降
【分析】(1)由题意可知,横轴表示季度,纵轴表示数量,纵轴单位长度表示100台,先根据表格中各季度销量画出各点,再依次连接各点,最后标注对应数据;
(2)各季度销量相加求出全年销售空调的总台数,一共4个季度,平均每个季度销售空调的台数=全年销售空调的总台数÷4;
(3)折线统计图中,折点位置最高表示该季度销量最高,折点位置最低表示该季度销量最低;
(4)折线统计图中,折线向上时,说明空调销量呈上升趋势,折线向下时,说明空调销量呈下降趋势,据此解答。
【详解】(1)分析可知:
(2)300+400+800+360
=(300+400+800)+360
=1500+360
=1860(台)
1860÷4=465(台)
所以,2021年全年一共销售空调1860台,平均每个季度销售空调465台。
(3)由折线统计图可知,第三季度销售空调最多,第一季度销售空调最少。
(4)由折线统计图可知,从第一季度到第三季度,华联购物中心的空调销售呈现上升趋势;从第四季度开始又呈现下降趋势。
【点睛】理解并掌握折线统计图的特点及作用,并且能够根据统计图提供的信息解决有关实际问题是解答题目的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末模拟测试卷-数学五年级上册青岛版
一、选择题
1.下列各式中,积最大的是( )。
A.1.6×3.05 B.160×0.305 C.1.6×0.305
2.循环小数0.3296296…中,小数点后面第99位上的数字是( )。
A.3 B.2 C.9 D.6
3.已知a=2×3×5,那么a的因数一共有( )个。
A.6 B.7 C.8
4.已知□+□+〇=19,□+〇=12,那么□和〇各是( )。
A.8和4 B.7和5 C.6和7
5.下面不适合用折线统计图表示是( )。
A.第27届—第32届夏季奥运会中国获得金牌数的变化情况。
B.2015年—2020年德州市接待游客人数的变化情况。
C.2020年山东省月降水量的变化情况。
D.2021年新冠肺炎全国各地感染人数。
6.如图,两个长方形完全相同,则阴影部分的面积( )。
A.甲>乙 B.甲<乙 C.甲=乙
二、填空题
7.我国的高铁向世界展示了“中国速度”。普通火车的速度是每小时120千米,高铁的速度可以达到普通火车的2.92倍,高铁的速度是( )千米/时。(得数保留整数)
8.在括号里填上“>”“<”或者“=”。
6.27×1.09( )6.27 4.2×0.7( )0.07×42 0.91÷0.7( )0.91
4.7×0.6( )4.7 9.63×1( )9.63÷1 11.4÷1.06( )11.4
9.选出两张不同的数字卡片,写出所有符合要求的两位数。
(1)组成的数是奇数:( );
(2)组成的数是5的倍数:( );
(3)组成的数既是2的倍数,又是5的倍数:( );
(4)组成的数既是奇数,又是5的倍数:( )。
10.
根据上图列方程( )。
11.一个三角形的底是25米,高是20米,面积是( )平方米,与这个三角形等底等高的平行四边形的面积是( )平方米。
12.一个梯形的面积是84平方米,高是4米,它的下底比上底多3米,这个梯形的上底是( )米.
三、判断题
13.在2.6×1.5+3.4×1.5=(2.6+3.4)×1.5中,运用了乘法结合律。( )
14.14.3535353535是循环小数。( )
15.方程与的解相同,则a等于18.2。( )
16.统计某地区2019年月平均气温变化情况用折线统计图比较好。( )
17.把一个长方形框架拉成一个平行四边形后,它的周长变了,面积没变。( )
四、计算题
18.直接写得数。
6.7+2.5= 3.4×8= 6.7÷2= 4.8÷0.06= 12.5×0.8+0.2=
8.5-5.8= 2.5×0.4= 5.2÷4= 3.5×6= 0.4×0.2÷0.4×0.2=
19.竖式计算。(带△的得数保留两位小数。)
①0.35×0.18= ②△8.05÷3.7≈
20.计算下列各题,能简算的要简算。
7.86×1.01-7.86 8.4÷0.21÷0.4 99×0.45+0.45
0.96÷[0.5×(6-2.8)] 5.6×102 3.2×2.4+32×0.76
21.解方程。(带☆的要检验)
☆
22.求下面组合图形的面积。(单位:厘米)
五、解答题
23.李老师打算买3盒钢笔奖励给表现优异的学生,一盒钢笔有12支,每支6.5元,买这些钢笔一共需要多少钱?
24.一辆汽车0.8小时行驶15.2千米,照这样计算,行驶228千米需要多少小时?
25.甲、乙两市相距855千米。一辆慢车从甲市开往乙市,每小时行60千米,3小时后,一辆快车从乙市开往甲市,每小时行75千米。快车开出几小时后两车相遇?(列方程解答)
26.甲、乙两地相距560千米,一辆客车和一辆货车同时从甲、乙两地相向而行,4小时后两车相遇。客车每小时行73.5千米,货车每小时行多少千米?
27.爷爷家有一块三角形的小麦地,底32米、高15米,今年一共收小麦134.4千克.平均每平方米收小麦多少千克?
28.华联购物中心2021年空调销售情况统计。
季度 第一季度 第二季度 第三季度 第四季度
数量(台) 300 400 800 360
(1)根据表中信息绘制折线统计图。
(2)2021年全年一共销售空调( )台,平均每个季度销售空调( )台。
(3)第( )季度销售空调最多,第( )季度销售空调最少。
(4)从第一季度到第三季度,华联购物中心的空调销售呈现( )趋势;从第四季度开始又呈现( )趋势。
参考答案:
1.B
【分析】小数乘法法则:
(1)按整数乘法法则先算出积。
(2)看因数中一共有几位小数,就从积的右边起,数出几位点上小数点。
据此计算出每个选项的具体数值,后比较大小即可。
【详解】由分析可得:
A.1.6×3.05=4.88
B.160×0.305=48.8
C.1.6×0.305=0.488
48.8>4.88>0.488
所以,积最大的是160×0.305。
故答案为:B
2.C
【分析】循环小数0.3296296…中,循环节是296,每3个数字一循环,因为小数点后面第一位是3,不参与循环,所以求小数点后面第99位上的数字,就是求(99-1)里面有几个3,用除法计算,然后根据余数的情况,判断出小数点后面第99位上的数字。
【详解】99-1=98
98÷3=32……2
余数是2表示是一个循环里的第2个数,即9;
所以小数点后面第99位上的数字是9。
故答案为:C
3.C
【分析】先根据a=2×3×5,求出a的值,再根据求一个数因数的方法,求出a的所有因数,即可解答。
【详解】a=2×3×5
a=6×5
a=30
30的因数有:1,2,3,5,6,10,15,30一共8个。
已知a=2×3×5,那么a的因数一共有8个。
故答案为:C
【点睛】求出a的值是解答本题的关键。
4.B
【分析】根据题意可知用19减去12即可求出□是几,用12减去□,即可求出〇是几,据此列式解答即可。
【详解】19-12=7
12-7=5
则□和〇各是7和5。
故答案为:B
5.D
【分析】根据折线统计图的特点可知:折线统计图不仅能够看出数量的多少,而且还能清楚地看出数量增减变化的情况。据此判断。
【详解】A. 第27届—第32届夏季奥运会中国获得金牌数的变化情况。有金牌数量的增减变化,可用折线统计图表示。
B. 2015年—2020年德州市接待游客人数的变化情况。有游客人数的增减变化,可用折线统计图表示。
C. 2020年山东省月降水量的变化情况。有月降水量的增减变化,可用折线统计图表示。
D. 2021年新冠肺炎全国各地感染人数。可用条形统计图直观表示出全国各地感染人数。
故答案为:D
【点睛】掌握折线统计图的特点是解答此类题的关键。
6.C
【分析】两个长方形完全相同,从图中可知,甲三角形的底等于长方形的长,高等于长方形的宽;乙三角形的底等于长方形的宽,高等于长方形的长;
根据长方形的面积=长×宽,三角形的面积=底×高÷2,可知甲、乙两个三角形的面积都等于长方形面积的一半,据此解答。
【详解】甲三角形的面积=长×宽÷2
乙三角形的面积=宽×长÷2
甲三角形的面积=乙三角形的面积=长方形面积的一半;
所以阴影部分的面积甲=乙。
故答案为:C
【点睛】找出两个阴影三角形的底、高与长方形的长、宽的关系是解题的关键。
7.350
【分析】根据小数乘法的意义,用120×2.92即可求出高铁的速度;保留两位整数就是精确到个位,要看十分位上的数字是几,然后根据四舍五入的方法取近似值。
【详解】120×2.92≈350(千米/时)
高铁的速度是350千米/时。
8. > = > < = <
【分析】(1)一个数(0除外)乘大于1的数,积比原来的数大;
(2)观察4.2×0.7和0.07×42,发现因数的数字都相同,只是小数位不同,根据“积的小数位数等于所有因数的小数位数之和”得出4.2×0.7的积和0.07×42的积都是两位小数,所以它们的积相等;
(3)一个数(0除外)除以小于1的数,商比原来的数大;
(4)一个数(0除外)乘小于1的数,积比原来的数小;
(5)一个数(0除外)乘1,积等于原来的数;
一个数(0除外)除以1,商等于原来的数;
(6)一个数(0除外)除以大于1的数,商比原来的数小。
【详解】(1)1.09>1,所以6.27×1.09>6.27;
(2)4.2×0.7=0.07×42
(3)0.7<1,所以0.91÷0.7>0.91;
(4)0.6<1,所以4.7×0.6<4.7;
(5)9.63×1=9.63÷1
(6)1.06>1,所以 11.4÷1.06<11.4。
9.(1)35、53、83、85
(2)35、30、50、85、80
(3)30、50、80
(4)35、85
【分析】奇数的特征:个位上是1、3、5、7、9的数;5的倍数特征:个位上是0或5的数;2的倍数特征:个位上是0、2、4、6、8的数;既是2的倍数,又是5的倍数:个位上是0的数;组成的数既是奇数,又是5的倍数:个位上是5的数,据此解答即可。
【详解】(1)组成的数是奇数:35、53、83、85;
(2)组成的数是5的倍数:35、30、50、85、80;
(3)组成的数既是2的倍数,又是5的倍数:30、50、80;
(4)组成的数既是奇数,又是5的倍数:35、85。
【点睛】本题考查2和5的倍数、奇数,解答本题的关键是掌握这些知识点。
10.
【分析】本子的价钱是未知数,根据本子的价钱和笔的价钱总共是20元列方程。
【详解】
【点睛】方程必须满足两个基本要素,必须是等式,必须含有未知数。
11. 250 500
【分析】已知三角形的底和高,根据三角形的面积=底×高÷2,代入数据计算即可求出这个三角形的面积。
根据三角形的面积=底×高÷2,平行四边形的面积=底×高,可知等底等高的平行四边形的面积是三角形面积的2倍,据此解答。
【详解】25×20÷2
=500÷2
=250(平方米)
250×2=500(平方米)
三角形的面积是250平方米,与这个三角形等底等高的平行四边形的面积是500平方米。
【点睛】本题考查三角形、平行四边形面积公式的运用,掌握等底等高的三角形和平行四边形面积之间的关系是解题的关键。
12.19.5
【解析】略
13.×
【分析】加法交换律:两个数相加,交换加数的位置,和不变。
乘法交换律:两个数相乘,交换两个因数的位置,积不变。
乘法结合律:三个数相乘,先乘前两个数,或者先乘后两个数,积不变。
乘法分配律:两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。
【详解】分析可知,在2.6×1.5+3.4×1.5=(2.6+3.4)×1.5中,运用了乘法分配律。
故答案为:×
14.×
【分析】小数分为有限小数和无限小数,小数部分的数位是有限的小数,叫做有限小数,小数部分的数位是无限的小数,叫做无限小数;循环小数是无限小数,再根据循环小数的意义以及特征:一个数的小数部分,从某一位起,一个数字或几个数字依次不断重复出现,这样的小数叫做循环小数,据此解答。
【详解】根据分析可知,14.3535353535是有限小数,不是循环小数。
原题干说法错误。
故答案为:×
15.√
【分析】根据等式的性质2,将左右两边同时乘8,即可求出x的值,因为方程与的解相同,则把x的值代入中,再根据等式的性质1和2进行解答即可。
【详解】
解:
解:
a等于18.2,原题说法正确。
故答案为:√
【点睛】本题考查了解方程的方法,掌握相应的计算方法是解答本题的关键。
16.√
【分析】折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况,由此解答即可。
【详解】因为要统计某地区一年12个月的月平均气温变化情况,所以选用折线统计图比较合适。
故答案为:√
【点睛】掌握折线统计图的特点是解答本题的关键。
17.×
【分析】把一个长方形框架拉成一个平行四边形,长方形的长相当于平行四边形的底,长方形的宽相当于平行四边形底边的邻边,则四条边的总长度不变,比较长方形的宽和平行四边形高的大小关系,确定长方形和平行四边形面积的大小关系即可。
【详解】分析可知,长方形的周长=平行四边形的周长
长方形的长=平行四边形的底,长方形的宽>平行四边形的高
长方形的面积=长×宽,平行四边形的面积=底×高
长×宽>底×高,则长方形的面积>平行四边形的面积
所以,把一个长方形框架拉成一个平行四边形,周长没变,面积变了,原题说法错误。
故答案为:×
【点睛】分析平行四边形的高与长方形宽的大小关系是解答题目的关键。
18.9.2;27.2;3.35;80;10.2
2.7;1;1.3;21;0.04
【解析】略
19.①0.063;②2.18
【分析】小数乘小数的计算方法,先按照整数乘法的计算方法计算,再看因数中共有几位小数,就从积的右边起数出几位点上小数点;
小数除法计算方法:在计算除数是小数的除法时。根据商不变的性质,将除数和被除数同时扩大相同的倍数,转化成除数是整数的除法进行计算;得数保留两位小数,看千分位上的数字是否满5,然后运用“四舍五入”法求得近似数即可。
【详解】① 0.35×0.18=0.063 ②△8.05÷3.7≈2.18
20.0.0786;100;45;
0.6;571.2;32
【分析】(1)运用乘法分配律进行计算即可;
(2)运用除法的性质进行计算即可;
(3)运用乘法分配律进行计算即可;
(4)先算小括号里面的减法,再算中括号里面的乘法,最后算括号外面的除法;
(5)把102拆成100+2,再运用乘法分配律进行计算即可;
(6)根据积不变的规律,把原式化为3.2×2.4+3.2×7.6,再运用乘法分配律进行计算即可。
【详解】7.86×1.01-7.86
=7.86×(1.01-1)
=7.86×0.01
=0.0786
8.4÷0.21÷0.4
=8.4÷(0.21×0.4)
=8.4÷0.084
=100
99×0.45+0.45
=(99+1)×0.45
=100×0.45
=45
0.96÷[0.5×(6-2.8)]
=0.96÷[0.5×3.2]
=0.96÷1.6
=0.6
5.6×102
=5.6×(100+2)
=5.6×100+5.6×2
=560+11.2
=571.2
3.2×2.4+32×0.76
=3.2×2.4+3.2×7.6
=3.2×(2.4+7.6)
=3.2×10
=32
21.;
【分析】根据等式的性质解方程。
(1)方程两边同时加上,求出方程的解;
(2)方程两边同时乘,求出方程的解。
【详解】(1)
解:
(2)
解:
检验:
方程左边
方程右边
所以,是方程的解。
22.696平方厘米
【分析】三角形的面积=底×高÷2,长方形的面积=长×宽,梯形的面积=(上底+下底)×高÷2,整个图形的面积=三角形的面积+长方形的面积+梯形的面积,据此解答。
【详解】8×10÷2+8×70+(8+16)×8÷2
=8×10÷2+8×70+24×8÷2
=40+560+96
=696(平方厘米)
所以,组合图形的面积是696平方厘米。
23.234元
【分析】用每盒钢笔的支数乘盒数,求出一共有多少支钢笔,再根据“单价×数量=总价”,代入数值求出一共需要的钱数即可。
【详解】
(元)
答:买这些钢笔一共需要234元钱。
24.12小时
【分析】根据速度=路程÷时间,代入数值,先求出速度,再根据时间=路程÷速度,代入数值即可求出行驶228千米需要多少小时。
【详解】228÷(15.2÷0.8)
=228÷19
=12(小时)
答:行驶228千米需要12小时。
25.5小时
【分析】由题意可知,根据速度×时间=路程,即用60乘3即可求出慢车3小时可行驶的距离,此时快车和慢车相遇的路程为855-60×3=675千米,设快车开出后x小时两车相遇,再根据等量关系:速度和×相遇时间=相遇的路程,据此列方程解答即可。
【详解】解:设快车开出后x小时两车相遇。
(60+75)x=855-60×3
(60+75)x=855-180
(60+75)x=675
135x=675
135x÷135=675÷135
x=5
答:快车开出5小时后两车相遇。
26.66.5千米
【分析】根据“速度×时间=路程”可得出等量关系:客车的速度×相遇时间+货车的速度×相遇时间=甲、乙两地的距离,据此列出方程,并求解。
【详解】解:设货车每小时行千米。
73.5×4+4=560
294+4=560
294+4-294=560-294
4=266
4÷4=266÷4
=66.5
答:货车每小时行66.5千米。
【点睛】本题考查列方程解决问题,根据速度、时间、路程之间的关系得出等量关系,按等量关系列出方程。
27.0.56千克
【分析】先利用三角形面积公式求出这块地的面积,总产量除以这块地的面积,就是每平方米的小麦产量。
【详解】134.4÷(32×15÷2)
=134.4÷240
=0.56(千克)
答:平均每平方米收小麦0.56千克。
【点睛】此题主要考查三角形的面积公式及“总产量÷总面积=单产量”。
28.(1)见详解;
(2)1860;465;
(3)三;一;
(4)上升;下降
【分析】(1)由题意可知,横轴表示季度,纵轴表示数量,纵轴单位长度表示100台,先根据表格中各季度销量画出各点,再依次连接各点,最后标注对应数据;
(2)各季度销量相加求出全年销售空调的总台数,一共4个季度,平均每个季度销售空调的台数=全年销售空调的总台数÷4;
(3)折线统计图中,折点位置最高表示该季度销量最高,折点位置最低表示该季度销量最低;
(4)折线统计图中,折线向上时,说明空调销量呈上升趋势,折线向下时,说明空调销量呈下降趋势,据此解答。
【详解】(1)分析可知:
(2)300+400+800+360
=(300+400+800)+360
=1500+360
=1860(台)
1860÷4=465(台)
所以,2021年全年一共销售空调1860台,平均每个季度销售空调465台。
(3)由折线统计图可知,第三季度销售空调最多,第一季度销售空调最少。
(4)由折线统计图可知,从第一季度到第三季度,华联购物中心的空调销售呈现上升趋势;从第四季度开始又呈现下降趋势。
【点睛】理解并掌握折线统计图的特点及作用,并且能够根据统计图提供的信息解决有关实际问题是解答题目的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
