专题 等边三角形与角平分线应用 人教版数学 八年级上册(含答案)
文档属性
| 名称 | 专题 等边三角形与角平分线应用 人教版数学 八年级上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 626.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-28 16:17:04 | ||
图片预览

文档简介
专题 等边三角形与角平分线应用
人教版数学 八年级上册
一、填空题
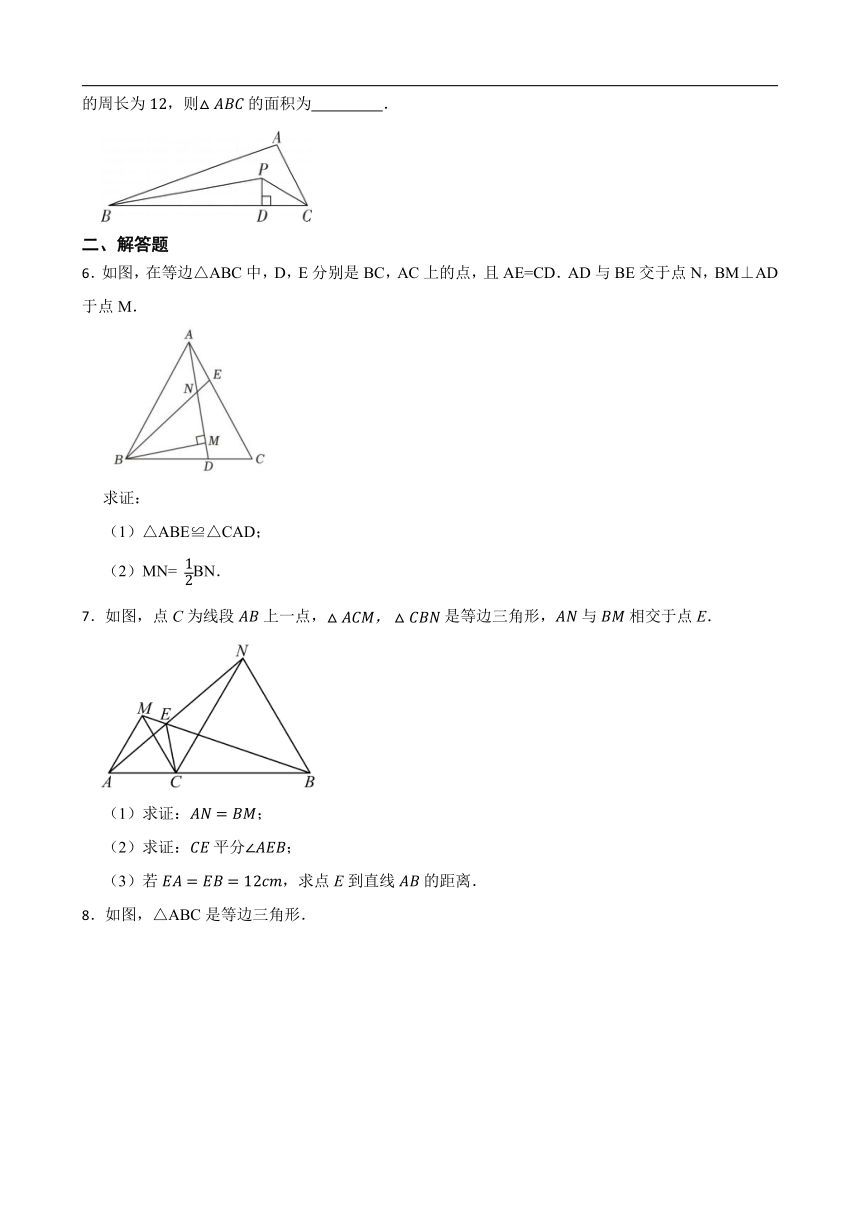
1.如图,在△ABC中,∠ABC=60°,∠BAC=75°,AD,CF分别是BC、AB边上的高且相交于点P,∠ABC的平分线BE分别交AD、CF于M、N.以下四个结论:①△PMN等边三角形;②除了△PMN外,还有4个等腰三角形;③△ABD≌△CPD;④当DM=2时,则DC=6.其中正确的结论是: (填序号).
2.如图,在中,的平分线交BC于点E,若,,则的周长为 .
3.如图,在中,和的平分线交于点于点,如果的面积是6,则的周长是 .
4.如图,在中,,是角平分线,若,,则的面积为 .
5.如图,在中,两条角平分线相交于点,过点作于点,若,的周长为,则的面积为 .
二、解答题
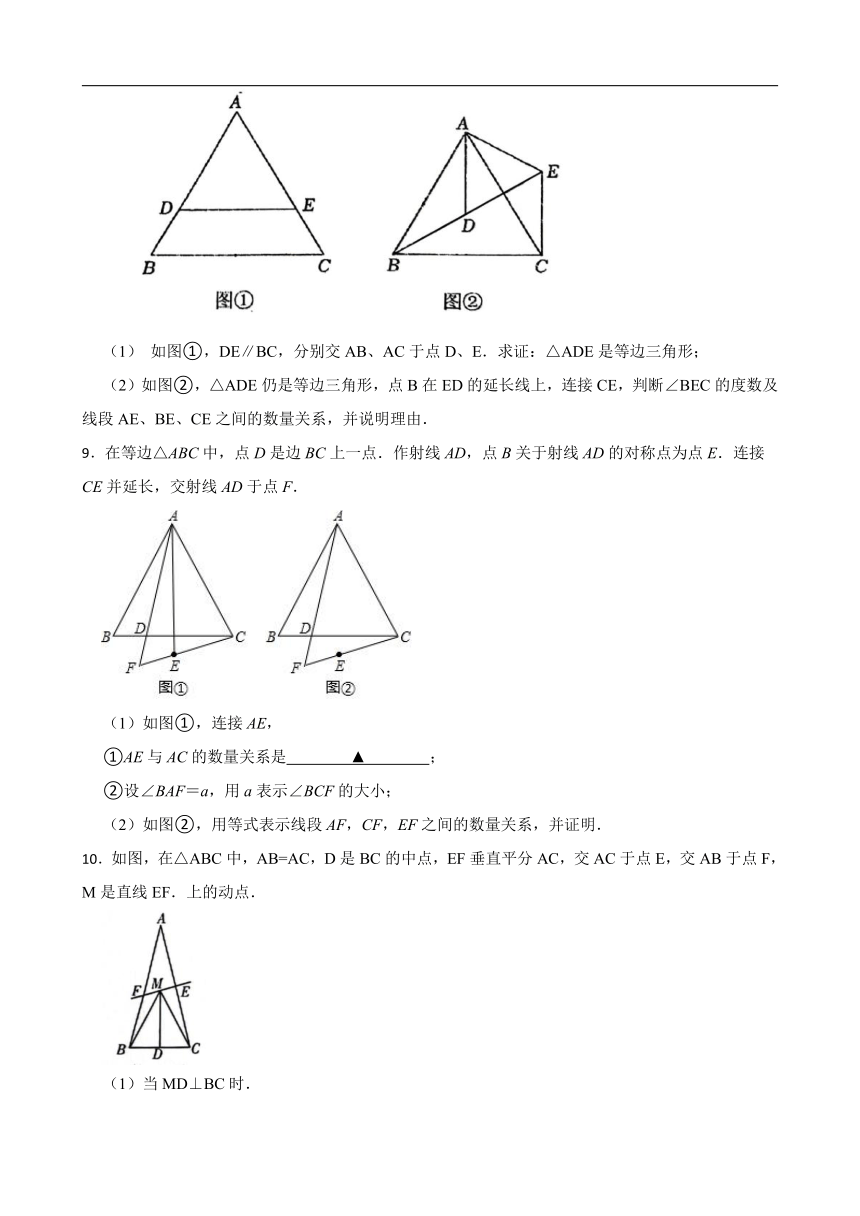
6.如图,在等边△ABC中,D,E分别是BC,AC上的点,且AE=CD.AD与BE交于点N,BM⊥AD于点M.
求证:
(1)△ABE≌△CAD;
(2)MN= BN.
7.如图,点C为线段上一点,是等边三角形,与相交于点E.
(1)求证:;
(2)求证:平分;
(3)若,求点E到直线的距离.
8.如图,△ABC是等边三角形.
(1) 如图①,DE∥BC,分别交AB、AC于点D、E.求证:△ADE是等边三角形;
(2)如图②,△ADE仍是等边三角形,点B在ED的延长线上,连接CE,判断∠BEC的度数及线段AE、BE、CE之间的数量关系,并说明理由.
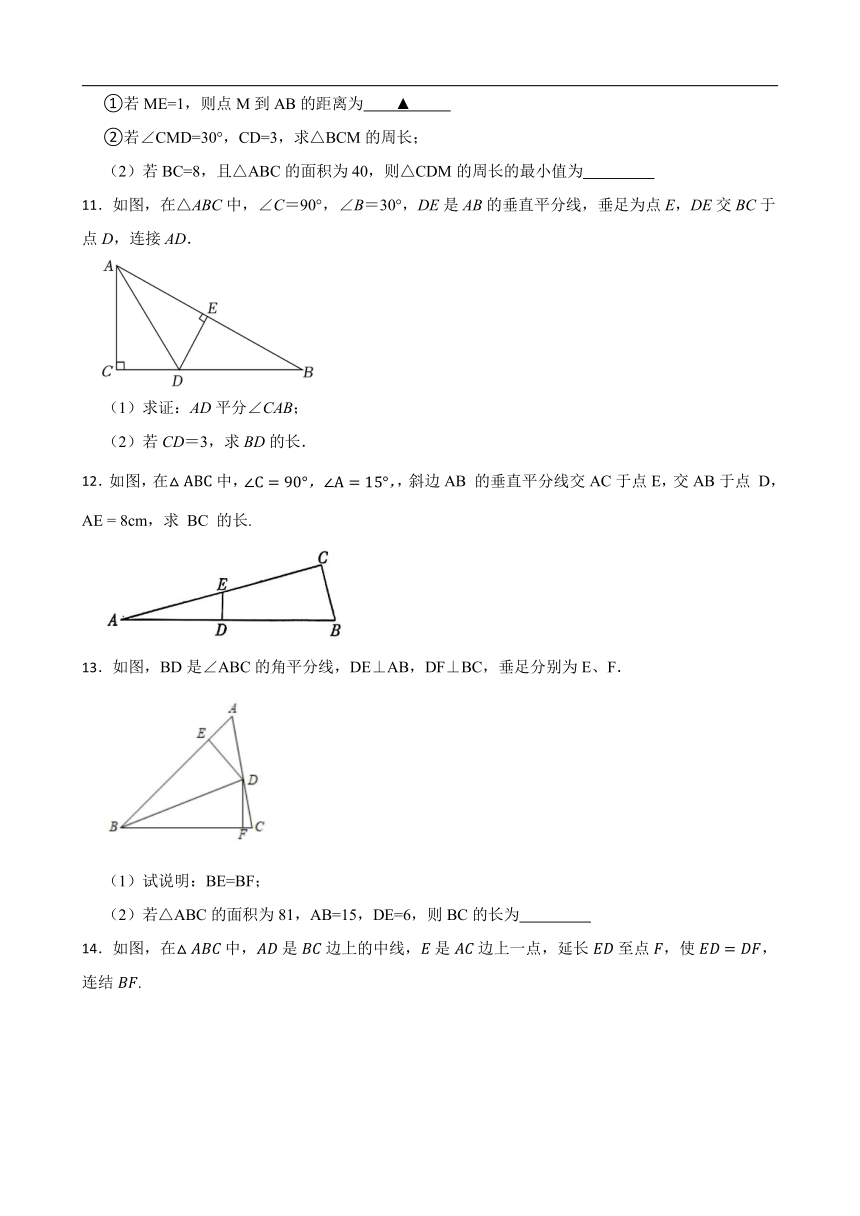
9.在等边△ABC中,点D是边BC上一点.作射线AD,点B关于射线AD的对称点为点E.连接CE并延长,交射线AD于点F.
(1)如图①,连接AE,
①AE与AC的数量关系是 ▲ ;
②设∠BAF=a,用a表示∠BCF的大小;
(2)如图②,用等式表示线段AF,CF,EF之间的数量关系,并证明.
10.如图,在△ABC中,AB=AC,D是BC的中点,EF垂直平分AC,交AC于点E,交AB于点F,M是直线EF.上的动点.
(1)当MD⊥BC时.
①若ME=1,则点M到AB的距离为 ▲
②若∠CMD=30°,CD=3,求△BCM的周长;
(2)若BC=8,且△ABC的面积为40,则△CDM的周长的最小值为
11.如图,在△ABC中,∠C=90°,∠B=30°,DE是AB的垂直平分线,垂足为点E,DE交BC于点D,连接AD.
(1)求证:AD平分∠CAB;
(2)若CD=3,求BD的长.
12.如图,在中,,斜边AB 的垂直平分线交AC于点E,交AB于点 D,AE = 8cm,求 BC 的长.
13.如图,BD是∠ABC的角平分线,DE⊥AB,DF⊥BC,垂足分别为E、F.
(1)试说明:BE=BF;
(2)若△ABC的面积为81,AB=15,DE=6,则BC的长为
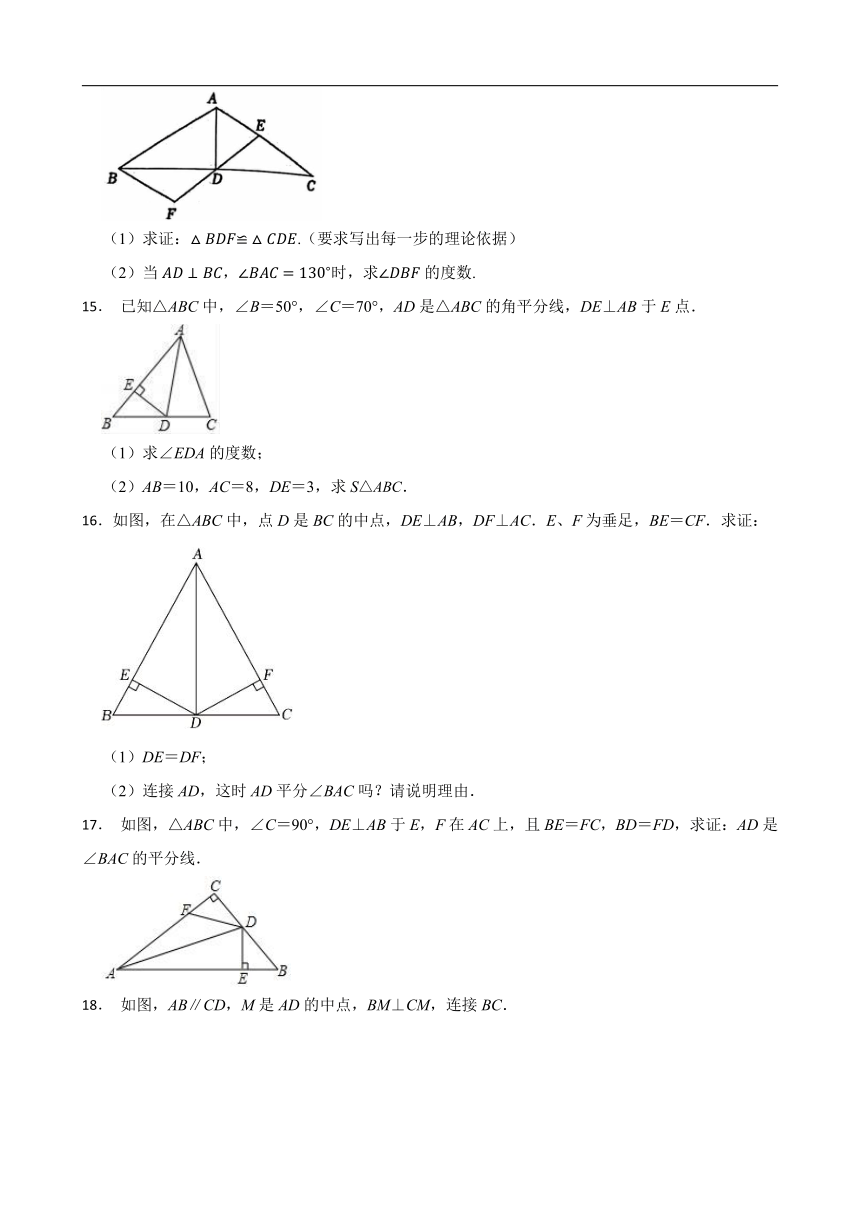
14.如图,在中,是边上的中线,是边上一点,延长至点,使,连结.
(1)求证:.(要求写出每一步的理论依据)
(2)当,时,求的度数.
15. 已知△ABC中,∠B=50°,∠C=70°,AD是△ABC的角平分线,DE⊥AB于E点.
(1)求∠EDA的度数;
(2)AB=10,AC=8,DE=3,求S△ABC.
16.如图,在△ABC中,点D是BC的中点,DE⊥AB,DF⊥AC.E、F为垂足,BE=CF.求证:
(1)DE=DF;
(2)连接AD,这时AD平分∠BAC吗?请说明理由.
17. 如图,△ABC中,∠C=90°,DE⊥AB于E,F在AC上,且BE=FC,BD=FD,求证:AD是∠BAC的平分线.
18. 如图,AB∥CD,M是AD的中点,BM⊥CM,连接BC.
(1)求证:CM平分∠BCD;
(2)探究BC、CD、AB之间的数量关系.
三、实践探究题
19.如图,点是等边内一点,是外的一点,,,≌,,连接.
(1)求证:是等边三角形;
(2)当时,试判断的形状,并说明理由;
(3)探究:当为多少度时,是等腰三角形.
20.
(1)【初步感知】
如图1,已知为等边三角形,点为边上一动点点不与点,点重合以为边向右侧作等边,连接.
求证:≌;
(2)【类比探究】
如图,若点在边的延长线上,随着动点的运动位置不同,猜想并证明:与的位置关系为: ;线段、、之间的数量关系为: ;
(3)【拓展应用】
如图,在等边中,,点是边上一定点且,若点为射线上动点,以为边向右侧作等边,连接、请问:是否有最小值?若有,请直接写出其最小值;若没有,请说明理由.
21.已知是的平分线,点P是射线上一点,点C,D分别在射线,上,连接,.
(1)【发现问题】
如图①,当,时,则与的数量关系是 .
(2)【探究问题】
如图②,点C,D在射线,上滑动,且,当时,与在【发现问题】中的数量关系还成立吗?说明理由.
22.【问题背景】
如图,在中,,和的平分线和相交于点G.
【问题探究】
(1)的度数为 ;
(2)过G作交的延长线于点F,交于点H,判断与的数量关系,并说明理由;
(3)在(2)的条件下,若,求的长.
答案解析部分
1.【答案】①②③④
2.【答案】52
3.【答案】12
4.【答案】18
5.【答案】6
6.【答案】(1)证明:∵△ABC是等边三角形,∴AB=BC=AC,∠BAC=∠ACB= 60°,
在△ABE和△CAD中,
∴△ABE≌△CAD (SAS)
(2)证明:∵△ABE≌△CAD,
∴∠ABE=∠CAD,
∴∠BNM=∠BAN+∠ABN=∠BAN+∠CAD=60°,
∵BM⊥AD,
∴∠AMB=90°,
∴∠NBM=30°,
∴MN= BN
7.【答案】(1)证明:∵是等边三角形,
∴.
∴.
∴.
∴.
∴.
(2)证明:过点C作,垂足分别为H,I,
∵,
∴
∴.
∴.
∴平分.
(3)解:如图,,
∵,
∴.
∵,
,
∴.
∴.
∵,
由(2)平分,
∴,.
∴.
∴.
∴点E到直线的距离为.
8.【答案】(1)解:∵是等边三角形,
∴∠A=∠B=∠C=60°,
∵DE∥BC,
∴∠ADE=∠AED=60°,
∴是等边三角形;
(2)∠BEC =60°,AE+CE=BE,
理由如下:
∵是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即:∠BAD=∠CAE,
∴,
∴∠ABD=∠ACE,BD=CE,
∴∠CBD+∠ACE=60°,
∴∠BEC=180°-(∠CBD+∠ACB+∠ACE)=180°-120°=60°,
∵BE=BD+DE,AE=DE,
∴AE+CE=BE.
9.【答案】(1)解:①∵点B关于射线AD的对称点为E,
∴AE=AB,
∵△ABC为等边三角形,
∴AB=AC,
∴AE=AC.
故答案为:AE=AC.
②解:∵∠BAF=∠EAF=α,△ABC是等边三角形,
∴AB=AC,∠BAC=∠ACB=60°,
∴∠EAC=60°﹣2α,AE=AC,
∴∠ACE= [180°﹣(60°﹣2α)]=60°+α,
∴∠BCF=∠ACE﹣∠ACB=60°+α﹣60°=α.
(2)解:结论:AF=EF+CF.
证明:如图,作∠FCG=60°交AD于点G,连接BF.
∵∠BAF=∠BCF=α,∠ADB=∠CDF,
∴∠ABC=∠AFC=60°,
∴△FCG是等边三角形,
∴GF=FC,
∵△ABC是等边三角形,
∴BC=AC,∠ACB=60°,
∴∠ACG=∠BCF=α,
在△ACG和△BCF中,
,
∴△ACG≌△BCF(SAS).
∴AG=BF,
∵点B关于射线AD的对称点为E,
∴BF=EF,
∴AF﹣AG=GF,
∴AF=EF+CF.
10.【答案】(1)解:①1;
②∵D是BC的中点,MD⊥BC.
∴MB =MC,∴MD平分∠BMC,∴∠BMC=2∠CMD=60°,
∴△BCM是等边三角形,
∴BC=BM=MC.
∵D是BC的中点,
∴BC=2CD=6,
∴△BCM的周长为BC+BM+MC=18.
(2)14
11.【答案】(1)证明:∵DE是AB的垂直平分线,
∴DB=DA,
∴∠DAB=∠DBA=30°.
∵∠C=90°,∠B=30°,
∴∠CAD=∠BAD=30°,
∴AD平分∠CAB.
(2)解:∵AD平分∠CAB,DC⊥AC,DE⊥AB,
∴DC=DE.
∵DC=DE,CD=3,
∴DE=3.
∵∠B=30°,DE⊥AB,
∴BD=2DE=6.
12.【答案】解:BC=4cm
13.【答案】(1)证明:∵BD是△ABC的角平分线,DE⊥AB, DF⊥BC,
∴∠DBE=∠DBF,∠BED=∠BFD=90°,在△BDE和△BDF中,
∴△BDE≌△BDF (AAS),∴BE=BF
(2)12
14.【答案】(1)证明:是边上的中线(已知).
(三角形中线的定义),
在和中,
,
;
(2)解:(已知),
(垂直的定义)
在和中,
(SAS)
(全等三角形的性质)
平分(角平分线的定义)
(已知)
(等量代换)
在中,(三角形内角和定理)
(等式的基本性质)
又(已证)
(全等三角形的性质)
15.【答案】(1)解:∵∠B=50°,∠C=70°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣50°﹣70°=60°,
∵AD是△ABC的角平分线,
∴∠BAD=∠BAC=×60°=30°,
∵DE⊥AB,
∴∠DEA=90°,
∴∠EDA=180°﹣∠BAD﹣∠DEA=180°﹣30°﹣90°=60°;
(2)解:如图,过D作DF⊥AC于F,
∵AD是△ABC的角平分线,DE⊥AB,
∴DF=DE=3,
又∵AB=10,AC=8,
∴S△ABC=×AB×DE+×AC×DF=×10×3+×8×3=27.
16.【答案】(1)解:∵D是BC的中点,
∴BD=CD,
∵DE⊥AB,DF⊥AC,
∴△BED和△CFD都是直角三角形,
在Rt△BED与Rt△CFD中,
,
∴Rt△BED≌Rt△CFD(HL),
∴DE=DF;
(2)解:AD平分∠BAC.
理由如下:∵DE=DF,DE⊥AB,DF⊥AC,
∴AD是△ABC的角平分线.
17.【答案】解:证明:在Rt△CDF和Rt△EDB中,
,
∴Rt△CDF≌Rt△EDB(HL),
∴DC=DE,
而DC⊥AC,DE⊥AB,
∴∠DAC=∠DAB,
即AD是∠BAC的平分线.
18.【答案】(1)证明:延长BM交CD于点N,如图:
∵AB∥CD,
∴∠A=∠D,∠ABM=∠DNM,
∵M是AD的中点,
∴AM=DM,
在△ABM和△DNM中,
∴△ABM≌△DNM(AAS),
∴BM=NM,
∵BM⊥CM,
∴∠CMB=∠CMN=90°,
又∵CM=CM,
∴△CBM≌△CNM(SAS),
∴∠BCM=∠NCM,即CM平分∠BCD.
(2)解:
19.【答案】(1)证明:≌,
.
,
是等边三角形.
(2)解:是直角三角形.
理由如下:
是等边三角形,
,
≌,,
,
,
是直角三角形.
(3)解:是等边三角形,
.
,,
,
,
.
当时,,
.
当时,,
.
当时,
,
.
综上所述:当或或时,是等腰三角形.
20.【答案】(1)证明:和是等边三角形,
,,,
,
即
在和中,
,
∴△ABD≌△ACE(SAS);
(2)平行;
(3)解:有最小值,
在BD延长线上截取,连接EM,
在和中,
,
∴,
,,
是等边三角形,
,
即点在角平分线上运动,
作点关于对称点,
连接与交于点,
此时点与点重合,
,
最小值为.
21.【答案】(1)
(2)解:点P点作于E,于F,
∴,
∵,,
∴,
又,
∴,
由(1)知:,
在和中
,
∴,
∴.
22.【答案】(1)135
(2)解:,理由如下:
∵,
∴,
∵,
∴,
又∵,
∴,
∵和的平分线和相交于点G,
∴,
∴,
又∵,
∴,
∴;
(3)解:∵,
∴,
∴,
又∵,
∴,
∴.
人教版数学 八年级上册
一、填空题
1.如图,在△ABC中,∠ABC=60°,∠BAC=75°,AD,CF分别是BC、AB边上的高且相交于点P,∠ABC的平分线BE分别交AD、CF于M、N.以下四个结论:①△PMN等边三角形;②除了△PMN外,还有4个等腰三角形;③△ABD≌△CPD;④当DM=2时,则DC=6.其中正确的结论是: (填序号).
2.如图,在中,的平分线交BC于点E,若,,则的周长为 .
3.如图,在中,和的平分线交于点于点,如果的面积是6,则的周长是 .
4.如图,在中,,是角平分线,若,,则的面积为 .
5.如图,在中,两条角平分线相交于点,过点作于点,若,的周长为,则的面积为 .
二、解答题
6.如图,在等边△ABC中,D,E分别是BC,AC上的点,且AE=CD.AD与BE交于点N,BM⊥AD于点M.
求证:
(1)△ABE≌△CAD;
(2)MN= BN.
7.如图,点C为线段上一点,是等边三角形,与相交于点E.
(1)求证:;
(2)求证:平分;
(3)若,求点E到直线的距离.
8.如图,△ABC是等边三角形.
(1) 如图①,DE∥BC,分别交AB、AC于点D、E.求证:△ADE是等边三角形;
(2)如图②,△ADE仍是等边三角形,点B在ED的延长线上,连接CE,判断∠BEC的度数及线段AE、BE、CE之间的数量关系,并说明理由.
9.在等边△ABC中,点D是边BC上一点.作射线AD,点B关于射线AD的对称点为点E.连接CE并延长,交射线AD于点F.
(1)如图①,连接AE,
①AE与AC的数量关系是 ▲ ;
②设∠BAF=a,用a表示∠BCF的大小;
(2)如图②,用等式表示线段AF,CF,EF之间的数量关系,并证明.
10.如图,在△ABC中,AB=AC,D是BC的中点,EF垂直平分AC,交AC于点E,交AB于点F,M是直线EF.上的动点.
(1)当MD⊥BC时.
①若ME=1,则点M到AB的距离为 ▲
②若∠CMD=30°,CD=3,求△BCM的周长;
(2)若BC=8,且△ABC的面积为40,则△CDM的周长的最小值为
11.如图,在△ABC中,∠C=90°,∠B=30°,DE是AB的垂直平分线,垂足为点E,DE交BC于点D,连接AD.
(1)求证:AD平分∠CAB;
(2)若CD=3,求BD的长.
12.如图,在中,,斜边AB 的垂直平分线交AC于点E,交AB于点 D,AE = 8cm,求 BC 的长.
13.如图,BD是∠ABC的角平分线,DE⊥AB,DF⊥BC,垂足分别为E、F.
(1)试说明:BE=BF;
(2)若△ABC的面积为81,AB=15,DE=6,则BC的长为
14.如图,在中,是边上的中线,是边上一点,延长至点,使,连结.
(1)求证:.(要求写出每一步的理论依据)
(2)当,时,求的度数.
15. 已知△ABC中,∠B=50°,∠C=70°,AD是△ABC的角平分线,DE⊥AB于E点.
(1)求∠EDA的度数;
(2)AB=10,AC=8,DE=3,求S△ABC.
16.如图,在△ABC中,点D是BC的中点,DE⊥AB,DF⊥AC.E、F为垂足,BE=CF.求证:
(1)DE=DF;
(2)连接AD,这时AD平分∠BAC吗?请说明理由.
17. 如图,△ABC中,∠C=90°,DE⊥AB于E,F在AC上,且BE=FC,BD=FD,求证:AD是∠BAC的平分线.
18. 如图,AB∥CD,M是AD的中点,BM⊥CM,连接BC.
(1)求证:CM平分∠BCD;
(2)探究BC、CD、AB之间的数量关系.
三、实践探究题
19.如图,点是等边内一点,是外的一点,,,≌,,连接.
(1)求证:是等边三角形;
(2)当时,试判断的形状,并说明理由;
(3)探究:当为多少度时,是等腰三角形.
20.
(1)【初步感知】
如图1,已知为等边三角形,点为边上一动点点不与点,点重合以为边向右侧作等边,连接.
求证:≌;
(2)【类比探究】
如图,若点在边的延长线上,随着动点的运动位置不同,猜想并证明:与的位置关系为: ;线段、、之间的数量关系为: ;
(3)【拓展应用】
如图,在等边中,,点是边上一定点且,若点为射线上动点,以为边向右侧作等边,连接、请问:是否有最小值?若有,请直接写出其最小值;若没有,请说明理由.
21.已知是的平分线,点P是射线上一点,点C,D分别在射线,上,连接,.
(1)【发现问题】
如图①,当,时,则与的数量关系是 .
(2)【探究问题】
如图②,点C,D在射线,上滑动,且,当时,与在【发现问题】中的数量关系还成立吗?说明理由.
22.【问题背景】
如图,在中,,和的平分线和相交于点G.
【问题探究】
(1)的度数为 ;
(2)过G作交的延长线于点F,交于点H,判断与的数量关系,并说明理由;
(3)在(2)的条件下,若,求的长.
答案解析部分
1.【答案】①②③④
2.【答案】52
3.【答案】12
4.【答案】18
5.【答案】6
6.【答案】(1)证明:∵△ABC是等边三角形,∴AB=BC=AC,∠BAC=∠ACB= 60°,
在△ABE和△CAD中,
∴△ABE≌△CAD (SAS)
(2)证明:∵△ABE≌△CAD,
∴∠ABE=∠CAD,
∴∠BNM=∠BAN+∠ABN=∠BAN+∠CAD=60°,
∵BM⊥AD,
∴∠AMB=90°,
∴∠NBM=30°,
∴MN= BN
7.【答案】(1)证明:∵是等边三角形,
∴.
∴.
∴.
∴.
∴.
(2)证明:过点C作,垂足分别为H,I,
∵,
∴
∴.
∴.
∴平分.
(3)解:如图,,
∵,
∴.
∵,
,
∴.
∴.
∵,
由(2)平分,
∴,.
∴.
∴.
∴点E到直线的距离为.
8.【答案】(1)解:∵是等边三角形,
∴∠A=∠B=∠C=60°,
∵DE∥BC,
∴∠ADE=∠AED=60°,
∴是等边三角形;
(2)∠BEC =60°,AE+CE=BE,
理由如下:
∵是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即:∠BAD=∠CAE,
∴,
∴∠ABD=∠ACE,BD=CE,
∴∠CBD+∠ACE=60°,
∴∠BEC=180°-(∠CBD+∠ACB+∠ACE)=180°-120°=60°,
∵BE=BD+DE,AE=DE,
∴AE+CE=BE.
9.【答案】(1)解:①∵点B关于射线AD的对称点为E,
∴AE=AB,
∵△ABC为等边三角形,
∴AB=AC,
∴AE=AC.
故答案为:AE=AC.
②解:∵∠BAF=∠EAF=α,△ABC是等边三角形,
∴AB=AC,∠BAC=∠ACB=60°,
∴∠EAC=60°﹣2α,AE=AC,
∴∠ACE= [180°﹣(60°﹣2α)]=60°+α,
∴∠BCF=∠ACE﹣∠ACB=60°+α﹣60°=α.
(2)解:结论:AF=EF+CF.
证明:如图,作∠FCG=60°交AD于点G,连接BF.
∵∠BAF=∠BCF=α,∠ADB=∠CDF,
∴∠ABC=∠AFC=60°,
∴△FCG是等边三角形,
∴GF=FC,
∵△ABC是等边三角形,
∴BC=AC,∠ACB=60°,
∴∠ACG=∠BCF=α,
在△ACG和△BCF中,
,
∴△ACG≌△BCF(SAS).
∴AG=BF,
∵点B关于射线AD的对称点为E,
∴BF=EF,
∴AF﹣AG=GF,
∴AF=EF+CF.
10.【答案】(1)解:①1;
②∵D是BC的中点,MD⊥BC.
∴MB =MC,∴MD平分∠BMC,∴∠BMC=2∠CMD=60°,
∴△BCM是等边三角形,
∴BC=BM=MC.
∵D是BC的中点,
∴BC=2CD=6,
∴△BCM的周长为BC+BM+MC=18.
(2)14
11.【答案】(1)证明:∵DE是AB的垂直平分线,
∴DB=DA,
∴∠DAB=∠DBA=30°.
∵∠C=90°,∠B=30°,
∴∠CAD=∠BAD=30°,
∴AD平分∠CAB.
(2)解:∵AD平分∠CAB,DC⊥AC,DE⊥AB,
∴DC=DE.
∵DC=DE,CD=3,
∴DE=3.
∵∠B=30°,DE⊥AB,
∴BD=2DE=6.
12.【答案】解:BC=4cm
13.【答案】(1)证明:∵BD是△ABC的角平分线,DE⊥AB, DF⊥BC,
∴∠DBE=∠DBF,∠BED=∠BFD=90°,在△BDE和△BDF中,
∴△BDE≌△BDF (AAS),∴BE=BF
(2)12
14.【答案】(1)证明:是边上的中线(已知).
(三角形中线的定义),
在和中,
,
;
(2)解:(已知),
(垂直的定义)
在和中,
(SAS)
(全等三角形的性质)
平分(角平分线的定义)
(已知)
(等量代换)
在中,(三角形内角和定理)
(等式的基本性质)
又(已证)
(全等三角形的性质)
15.【答案】(1)解:∵∠B=50°,∠C=70°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣50°﹣70°=60°,
∵AD是△ABC的角平分线,
∴∠BAD=∠BAC=×60°=30°,
∵DE⊥AB,
∴∠DEA=90°,
∴∠EDA=180°﹣∠BAD﹣∠DEA=180°﹣30°﹣90°=60°;
(2)解:如图,过D作DF⊥AC于F,
∵AD是△ABC的角平分线,DE⊥AB,
∴DF=DE=3,
又∵AB=10,AC=8,
∴S△ABC=×AB×DE+×AC×DF=×10×3+×8×3=27.
16.【答案】(1)解:∵D是BC的中点,
∴BD=CD,
∵DE⊥AB,DF⊥AC,
∴△BED和△CFD都是直角三角形,
在Rt△BED与Rt△CFD中,
,
∴Rt△BED≌Rt△CFD(HL),
∴DE=DF;
(2)解:AD平分∠BAC.
理由如下:∵DE=DF,DE⊥AB,DF⊥AC,
∴AD是△ABC的角平分线.
17.【答案】解:证明:在Rt△CDF和Rt△EDB中,
,
∴Rt△CDF≌Rt△EDB(HL),
∴DC=DE,
而DC⊥AC,DE⊥AB,
∴∠DAC=∠DAB,
即AD是∠BAC的平分线.
18.【答案】(1)证明:延长BM交CD于点N,如图:
∵AB∥CD,
∴∠A=∠D,∠ABM=∠DNM,
∵M是AD的中点,
∴AM=DM,
在△ABM和△DNM中,
∴△ABM≌△DNM(AAS),
∴BM=NM,
∵BM⊥CM,
∴∠CMB=∠CMN=90°,
又∵CM=CM,
∴△CBM≌△CNM(SAS),
∴∠BCM=∠NCM,即CM平分∠BCD.
(2)解:
19.【答案】(1)证明:≌,
.
,
是等边三角形.
(2)解:是直角三角形.
理由如下:
是等边三角形,
,
≌,,
,
,
是直角三角形.
(3)解:是等边三角形,
.
,,
,
,
.
当时,,
.
当时,,
.
当时,
,
.
综上所述:当或或时,是等腰三角形.
20.【答案】(1)证明:和是等边三角形,
,,,
,
即
在和中,
,
∴△ABD≌△ACE(SAS);
(2)平行;
(3)解:有最小值,
在BD延长线上截取,连接EM,
在和中,
,
∴,
,,
是等边三角形,
,
即点在角平分线上运动,
作点关于对称点,
连接与交于点,
此时点与点重合,
,
最小值为.
21.【答案】(1)
(2)解:点P点作于E,于F,
∴,
∵,,
∴,
又,
∴,
由(1)知:,
在和中
,
∴,
∴.
22.【答案】(1)135
(2)解:,理由如下:
∵,
∴,
∵,
∴,
又∵,
∴,
∵和的平分线和相交于点G,
∴,
∴,
又∵,
∴,
∴;
(3)解:∵,
∴,
∴,
又∵,
∴,
∴.
