2024河南中考数学专题复习第二部分 题型一 真实问题情境 课件 58张PPT
文档属性
| 名称 | 2024河南中考数学专题复习第二部分 题型一 真实问题情境 课件 58张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-28 16:25:29 | ||
图片预览










文档简介
(共58张PPT)
真实问题情境
题型一
文件解读
考情及趋势分析
教育部 2019年11 月发布的《关于加强初中学业水平考试命题工作的意见》和 2022年版《义务教育数学课程标准》中均指出:情境创设的真实性.
考情分析 年份 题号 题型 分值 情境 设问
2023 (10次) 2 选择题 3 实物背景北宋时期的汝官窑天蓝釉刻花鹅颈瓶 关于三视图说法正确的是
8 选择题 3 实际问题(七、八年级选择电影观看) 两个年级选择影片相同的概率
11 填空题 3 某校给每个年级配发劳动工具 3个年级需要配发多少套劳动工具
考情分析 年份 题号 题型 分值 情境 设问
2023(10次) 13 填空题 3 探究“无絮杨”品种苗的生长规律 估计不低于300 cm的“无絮杨”品种有多少棵
17 解答题 9 从甲、乙两家快递公司选一家合作配送樱桃 (1)填空:中位数的计算、方差的大小比较;(2)(3)开放性设问
19 解答题 9 小军借助反比例函数设计“鱼形”图案 (1)求k的值;(2)求扇形半径和圆心角度数;(3)直接写出阴影部分的面积之和
20 解答题 9 用自制的测高仪测树高 求树的高度
考情分析 年份 题号 题型 分值 情境 设问
2023(10次) 21 解答题 9 购买健身器材的优惠活动 (1)一定条件下的最优方案选择;(2)两种活动付款金额相等求原价;(3)一定条件下求原价的取值范围
22 解答题 10 羽毛球的击球路线 (1)求点P的坐标和字母的值;(2)计算一定条件下的方案选择
23 解答题 10 以“图形的变化”为主题设计的问题 (1)旋转角度,平移距离;(2)①判断两个角度的数量关系,②两点的距离;(3)一定条件下求线段长
2022(9次) 7 选择题 3 课后延时服务打分 所打分数的众数为
10 选择题 3 呼气式酒精测试仪 下列说法不正确的是
考情分析 年份 题号 题型 分值 情境 设问
2022(9次) 13 填空题 3 实际问题(选取两名宣讲员) 恰好选中甲和丙的概率
17 解答题 9 航空航天知识掌握情况 (1)填空:中位数的计算、百分比;(2)考查中位数的意义;(3)开放性设问
19 解答题 9 开封清明上河园拂云阁 求拂云阁的高度
20 解答题 9 让学生体验农耕劳动 (1)菜苗单价;(2)购买最少花费
21 解答题 9 喷水景观 (1)抛物线表达式;(2)小红与爸爸的水平距离
22 解答题 10 滚铁环 (1)求证两角之和等于90°;(2)一定条件下求线段长
考情分析 年份 题号 题型 分值 情境 设问
2022(9次) 23 解答题 10 以“矩形的折叠”为主题展开数学活动 (1)写出30°的角;(2)①求角度;②角之间的数量关系;(3)一定条件下求线段长
2021(7次) 8 选择题 3 卡片(北斗、天问、高铁、九章) 恰好选中天问和九章的概率
13 填空题 3 甲、乙两个厂家提供货源 更符合规格要求的厂家
15 填空题 3 小华用一张直角三角形纸片玩折纸游戏 求线段的长
17 解答题 9 了解学生睡眠时间情况 (1)填空:中位数的计算、百分比;(2)开放性设问
考情分析 年份 题号 题型 分值 情境 设问
2021(7次) 19 解答题 9 龙门石窟卢舍那佛像 求佛像的高度
20 解答题 9 “石磨原理”跨物理学科“连杆” (1)证明两个角的倍数关系;(2)求线段长
21 解答题 9 在网店购买A,B两款猕猴玩偶 (1)购进玩偶个数;(2)设计进货方案获得最大利润;(3)根据利润率判断哪次购买更合算
2020(6次) 8 选择题 3 我国快递业务2017年至2019年收入 可列方程为
17 解答题 9 山药粉加工厂对甲、乙两台不同品牌分装机的选择 (1)填空:中位数的计算、不合格率;(2)方差的意义
考情分析 年份 题号 题型 分值 情境 设问
2020(6次) 18 解答题 9 观星台 (1)求观星台最高点距离地面的高度;(2)提减少误差的建议
19 解答题 9 健身房暑期优惠活动 (1)(2)考查函数关系式并说明实际意义;(3)选取哪种方案所需费用最少
2020(6次) 20 解答题 9 “三分角器”的原理与使用方法的材料阅读 补充已知条件和求证
22 解答题 10 小亮遇到问题结合学习函数的经验研究问题 (1)①补充表中的值;②对得到的结论说明理由;(2)画图;(3)一定条件下求线段长
命题趋势·新考法分析
从2019年全国政策文件中提到关于真实问题情境(包含生活情境、科学情境、文化情境、数学情境),河南试题就开始注重考查真实问题情景试题,通过研究近几年全国考查的真实问题情境类试题,情境可分为下面几类:1. 背景情境:也就是我们常说的扣帽子的形式,情境与解题无关(如2023山西10题);2. 应用情境:这类试题情境与设问、图形相关,联系紧密,但仅停留在数学问题上(如2023北京21题);3. 实践应用:该类试题情境与设问强关联,且设问的提出、模型的构成均是来源于现实生活,且对现实生活具有一定的指导价值(如2023河南22题 ,2023甘肃省卷22题,2023舟山22题).从河南的中招考试分析,我们更应该关注第三类——实践应用的试题,真实情境试题设问回归情境,提出与情境关联性强,且具有实际意义,利用已有的数学知识或创造性的方法解决问题.将所得的数学答案放回真实情境之中,结合实际情况可判断答案是否符合实际或令人满意,反思是否还存在其他可能.
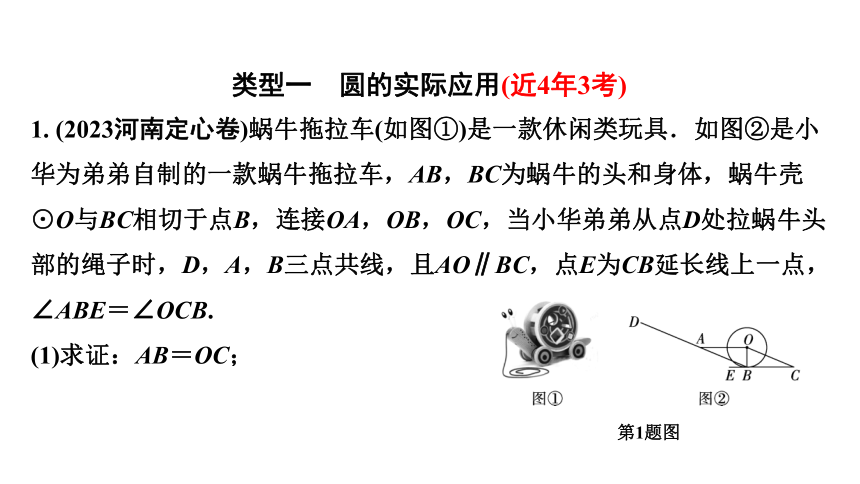
类型一 圆的实际应用(近4年3考)
1. (2023河南定心卷)蜗牛拖拉车(如图①)是一款休闲类玩具.如图②是小华为弟弟自制的一款蜗牛拖拉车,AB,BC为蜗牛的头和身体,蜗牛壳⊙O与BC相切于点B,连接OA,OB,OC,当小华弟弟从点D处拉蜗牛头部的绳子时,D,A,B三点共线,且AO∥BC,点E为CB延长线上一点,∠ABE=∠OCB.
(1)求证:AB=OC;
第1题图
(1)证明:∵∠ABE=∠OCB,
∴AB∥OC,
又∵AO∥BC,
∴四边形ABCO为平行四边形,
∴AB=OC;
第1题图
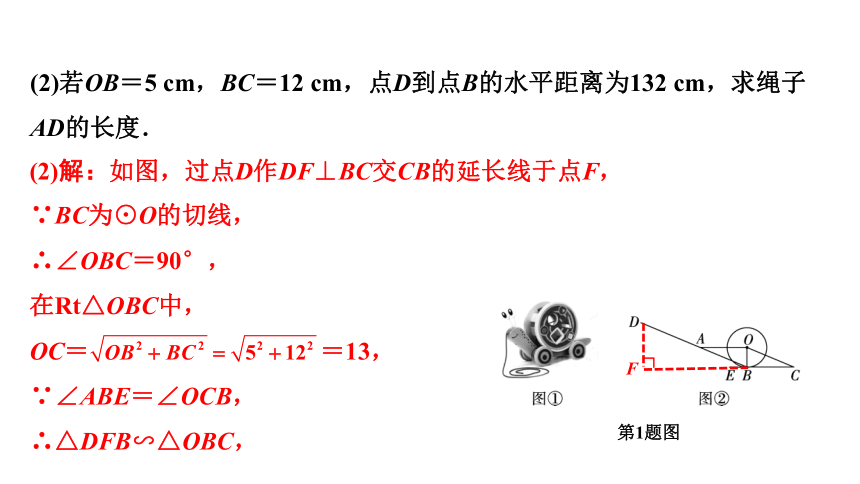
(2)若OB=5 cm,BC=12 cm,点D到点B的水平距离为132 cm,求绳子AD的长度.
第1题图
(2)解:如图,过点D作DF⊥BC交CB的延长线于点F,
∟
F
∵BC为⊙O的切线,
∴∠OBC=90°,
在Rt△OBC中,
OC= =13,
∵∠ABE=∠OCB,
∴△DFB∽△OBC,
∴ ,
即 ,
解得DB=143,
由(1)得AB=OC=13,
∴AD=DB-AB=143-13=130 cm.
第1题图
∟
F
2. (2023河南定心卷)如图①,太阳能热水器是指利用阳光中蕴含的能量将水加温的设备,属于可再生能源技术的一种.小明画出了热水器的示意图如图②所示,圆为水箱,AB为集热板,CD,AE为支架,CD垂直于屋面BC,延长BA与CD的延长线恰好交于圆上一点F,AE与圆相切于点A,经测量∠AEF=∠B.
(1)求证:BF过圆的圆心;
第2题图
(1)证明:由题意可知∠C=90°,
∴∠B+∠BFC=90°,
∵∠AEF=∠B,
∴∠AEF+∠BFC=90°,
∴∠FAE=90°,
∵AE是圆的切线,切点为A,
∴FA是圆的直径,
∴BF过圆的圆心;
第2题图
(2)若经测量热水器水箱直径长60 cm,∠B=60°,CD=136 cm,求热水器高度.
第2题图
(2)解:如图,连接AD,取AF的中点为点O,过点O分别作OH⊥BC于点H并交AD于点P,OG⊥FC交FC于点G,
O
∟
G
∟
H
P
则四边形OGCH为矩形,
∵CD=136,
∴PH=136,
∵AF为⊙O的直径,
∴∠ADF=90°,
∵∠C=90°,
∴AD∥BC,
∴∠FAD=∠B,
∵∠B=60°,
∴sin∠FAD=sinB= ,
即 ,
∵AF=60,
∴FD=30 ,OA=30,
第2题图
O
∟
G
∟
H
P
∵OH⊥BC,AD∥BC,
∴∠OPA=∠OHB=90°,
∵∠OAP=∠FAD,
∴△OAP∽△FAD,
∴ ,
∴OP=15 ,
∴热水器的高度为30+15 +136=(166+15 )cm.
第2题图
O
∟
G
∟
H
P
3. 如图①,过山车是一种机动游乐设施,常见于游乐园和主题乐园中,深受许多年轻游客的喜爱.如图②,过山车的轨道近似看成⊙O ,轨道的支撑AB,CD均与地面BC垂直,且与相切,点E为CD上一点,连接AE交⊙O 于点F,连接DF并延长与BC交于点G.已知AB=AD.
(1)求证:△ADE≌△DCG;
第3题图
(1)证明:∵AB,CD均与地面BC垂直,
且与⊙O相切,
∴∠ADE=∠DCG=∠ABC=∠BAD=90°,
∴四边形ABCD为矩形,∠ADF+∠CDG=90°,
∴AB=CD,
∵点F在⊙O上,AD为⊙O的直径,
∴∠AFD=90°,
∴∠DAE+∠ADF=90°,
∴∠CDG=∠DAE,
∵AB=AD,
∴AD=CD,
在△ADE与△DCG中,
第3题图
∴△ADE≌△DCG(ASA);
第3题图
(2)若DE=2 ,⊙O的半径为3,求AF的长.
第3题图
(2)解:由(1)知∠ADE=90°,∠AFD=90°,
∵DE=2 ,⊙O的半径为3,
∴AD=6,
在Rt△ADE中,
由勾股定理得AE= ,
在△ADE中,
根据三角形面积公式可知
AD·DE= AE·DF,
∴DF= =3,
∴在Rt△ADF中,
由勾股定理得AF= .
第3题图
4. (2023河南黑白卷)如图①是少年宫科技发明小组制作的一个钟表,钟面的大小会随时间的变化而发生改变.钟表底座为两根金属滑槽MN和GH,且MN⊥GH交于点O,钟面由若干个形如菱形ABCD的可活动木条组成,指针OP绕点O转动,菱形的顶点点B与点P用连杆连接.如图②,⊙O为P点的运动轨迹,⊙O与OH交于点E,连接PE,当BP与⊙O相切时,点A,B,P恰好在同一条直线上.
请仅就图②的情形解答下列问题:
第4题图
(1)求证:∠PBO+2∠PEO=90°;
第4题图
(1)证明:如图,连接OP,
∵BP与⊙O相切,
∴OP⊥BP,
∴∠PBO+∠BOP=90°,
∵OP=OE,
∴∠OPE=∠PEO,
∴∠BOP=∠OPE+∠PEO=2∠PEO,
∴∠PBO+2∠PEO=90°;
(2)若AB=OE=3,BP=4,求OD的长.
第4题图②
(2)解:在Rt△BOP中,OB= =5.
如图,过点A作AQ⊥BD于点Q,
∟
Q
∵四边形ABCD为菱形,
∴BD=2BQ,
∵AQ⊥BD,
∴∠AQB=90°,
∵∠ABQ=∠OBP,
由(1)知∠BPO=90°,
∴∠AQB=∠BPO=90°,
∴△ABQ∽△OBP,
∴ ,
∴BQ= ,
∴BD=2BQ= ,
∴OD=OB+BD=5+ = .
第4题图②
∟
Q
类型二 几何测量问题(9年9考)
1. 某数学兴趣小组计划测量学校教学楼的高度,他们在阳光下进行测量,如图,是同一时刻测量活动场景抽象出的平面几何图形,教学楼AB的影长为65 m,在教学楼影子末端点C处放着测角仪CD,CD的长为1.5 m,测角仪的影长CE为2. 3 m,且
AB EC,CD LEC,点B,C,E在同一直线
上,求教学楼的高度(结果保留整数).
⊥
⊥
第1题图
解:由题意得∠ABC=∠DCE=90°,AC∥DE,
∴∠ACB=∠DEC,
∴△ACB∽△DEC,
∴ ,
∴ ,
∴AB≈42(m),
答:教学楼的高度约为42 m.
第1题图
2. 如图①,中原大佛,位于河南省平顶山市鲁山县赵村乡上汤村佛泉寺,是世界上最高的佛教造像。某数学活动小组在学习完“锐角三角函数”之后,决定测量中原大佛的高度。为了减小误差,该数学活动小组在测量仰角的度数以及两个测量点之间的距离时,都分别测量了两次并取它们的平均值作为测量结果,测量数据如下
表(不完整):
第2题图①
活动课题 测量中原大佛的高度 活动工具 测角仪和皮尺 测量 示意图 说明:如图②,AB是中原大佛的截面图,他们先在点C处用高为1.5 m的测角仪CE测得塔顶点A的仰角∠AEF的度数,然后沿CB向D处前进,到达点D后用同样的测角仪从点D处测得点A的仰角∠AFG的度数,CD之间的距离可以直接测得,且点A,B,C,D,E,F,G在同一竖直平面内
第2题图①
第2题图②
测量 数据 测量项目 第一次 第二次 平均值
∠AEF 39.8° 40.2° 40°
∠AFG 44.7° 45.3° 45°
C,D之间 的距离 39.2 m 39.4 m ____ m
… (1)两次测量C,D之间的距离的平均值是__________m;
39.3
第2题图②
(2)根据以上测量结果,请你帮助该数学活动小组计算中原大佛AB的高度.(结果精确到1 m,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
(2)由题意得CE⊥CB,DF⊥CB,AB⊥CB,四边形EFDC为矩形,∠AEF=40°,∠AFG=45°,CD=EF=39.3 m,
∵∠AFG=45°,∴AG=FG.
设AG=FG=x,则EG=(x+39.3)m.
在Rt△AEG中,tan∠AEF=tan40°= ≈0.84,
解得x≈206.3.
第2题图②
经检验,x=206.3是原分式方程的解.
∴AB=AG+BG=206.3+1.5≈208(m).
答:中原大佛AB的高度约为208 m.
第2题图②
3. 小明利用所学知识来测量操场上的一个照明灯的高度.如图所示,矩形PDCQ为照明灯AB一侧观礼台的竖直截面示意图,他先到观礼台底部点C处,用测角仪CE测得照明灯顶端点A的仰角为45°,再在平台上点D处放置一个平面镜,在距平面镜1.7 m 的点G处恰好看到照明灯顶端点A,此时小明眼睛到观礼台的高度FG为1.6 m,
其中点Q,C,B在同一直线上,AB BC, FG DG,
EC BC.已知测角仪CE的高度为1.5 m,观礼台CD
的高度为2 m,求照明灯的高AB.(平面镜的大小,
测角仪的宽度忽略不计)
⊥
⊥
⊥
第3题图
第3题图
解:如图,分别过点D,E作AB的垂线,垂足分别为M,N,
∟
M
∟
N
∵AB⊥BC,四边形PQCD为矩形,
∴DC⊥BC,
∴四边形DMNE,四边形ENBC均为矩形,
∴DM=EN=CB,CE=BN,DE=MN,
∵∠AEN=45°,
∴EN=AN,
设DM=x,则CB=EN=AN=x,
∵DC=2,CE=1.5,
∴MN=DE=DC-EC=0.5,
∴AM=AN-MN=x-0.5,
由平面镜反射可得,∠FDG=∠ADM,
∵∠FGD=∠AMD=90°,
∴△ADM∽△FDG,
∴ ,即 ,解得x=8.5,
第3题图
∟
M
∟
N
∴AB=8.5+1.5=10,
答:照明灯的高AB为10 m.
4. (2023河南定心卷)2023年3月15日新晋高速公路全线通车,从陵川县到河南省新乡市也将从过去的3个多小时缩短至1个多小时,沿线共11座隧道.如图①,前期开挖其中一条隧道时,为了估算工程量,需要测量山两端AB的长,如图②,在山外一点C处测得点A位于点C的西北方向,点B位于点C的北偏东37°方向,并测得AC的距离为141 m,BC的距离为500 m,求山两端AB的长(结果精确到1 m,
参考数据:sin37°≈0.60,cos37°≈0.80,
tan37°≈0.75, ≈1.41).
第4题图
第4题图②
解:如图,过点C作东西方向水平线DE,过点A作AD⊥DE于点D,过点B作BE⊥DE于点E,
D
E
∟
∟
由题意可知,∠ACD=45°,∠CBE=37°,AC=141,BC=500,
在Rt△ACD中,sin∠ACD= ,cos∠ACD= ,
∴AC= = CD= AD=141≈100 ,
∴CD=AD≈100,
在Rt△BCE中,sin∠CBE= ,
cos∠CBE= ,
∴CE=BC·sin∠CBE=500sin37°,
BE=BC·cos∠CBE=500cos37°,
过点A作AF⊥BE交BE于点F,
第4题图②
D
E
∟
∟
∟
F
∴四边形ADEF为矩形,
∴AF=DE,AD=EF,
在Rt△ABF中,
AB=
≈500 m.
答:山两端AB的长约为500 m.
类型三 抛物线型的实际应用(近2年连续考查)
1. (2023河南黑白卷)如图①,一小球从静止沿斜坡下滑,小球离开桌面时做平抛运动(不考虑空气阻力),用频闪照相机观测到小球运动过程中的几个位置,并用平滑曲线连接得到小球平抛运动的轨迹.如图②,以小球滚出桌面的水平方向为x轴正方向,竖直向上方向为y轴正方向,小球离开桌面的位置为原点建立平面直角坐标系(小球的体积忽略不计),得到小球的位置坐标(x,y),根据平抛运动可知x,y与时
间t的关系如下: 已知桌面的高度为100
厘米,观测到三个时刻小球的位置坐标如下表:
第1题图
t(秒) 1 2 3
x(厘米) 10 20 30
y(厘米) -5 -20 -45
(1)求v和g的值;
第1题图
解:(1)∵x=vt,
∴将(1,10)代入x=vt中,得v=10,
∵y=- gt2,
∴将(1,-5)代入y=- gt2中,得g=10,
∴v=10,g=10;
(2)求小球做平抛运动时,运动轨迹所形成的抛物线的解析式;
第1题图
(2)∵v=10,g=10,
∴x=10t,y=-5t2,
∴y关于x的解析式,
即做平抛运动的运动轨迹所形成的
抛物线解析式为y=- ;
(3)小球水平抛出的正前方有一高为20厘米的正方体纸箱(纸箱厚度忽略不计),若要使小球落入纸箱中,求纸箱左侧到桌子的水平距离L的取值范围.
第1题图
(3)∵桌面的高度为100厘米,正方体纸箱的高度为20厘米,小球要落入纸箱,则小球要在y=-80时进入纸箱,
∴将y=-80代入y=- ,解得x=40(负值已舍去),
∵正方体纸箱的高度为20厘米,
∴纸箱左侧到桌子的最短水平距离
为40-20=20(厘米),
∴纸箱到桌子的水平距离L的取值范围为
20厘米<L<40厘米.
2. (2023河南定心卷)中考体育考试规定男生立定跳远满分为2.5 m,如图①,小勇立定跳远为2.4 m,小聪发现小勇立定跳远时脚的运动轨迹可近似看作抛物线,通过电子仪器测量得到小勇跳远时脚离地面的最高距离为72 cm,如图②,以小勇起跳点为原点建立平面直角坐标系,小勇落地点为A,最高点为B.
第2题图
(1)求小勇跳远时抛物线的表达式;
第2题图
解:(1)设抛物线的表达式为y=a(x-h)2+k(a≠0),
由题意知,点B(1.2,0.72)是抛物线的顶点,
∴y=a(x-1.2)2+0.72,
又∵抛物线经过点A(2.4,0),
∴0=a(2.4-1.2)2+0.72,
解得a=-0.5,
∴抛物线的表达式为y=-0.5(x-1.2)2+0.72
(或y=-0.5x2+1.2x);
(2)①由题意知,
小勇调整跳远姿势后新抛物线过原点(0,0),
∴设新抛物线表达式为y=mx2+bx,
∵抛物线经过点(2.5,0),
把(2.5,0)代入y=mx2+bx中,
(2)体育老师告诉小勇他的跳远姿势不对,调整跳远姿势后,小勇恰好跳到了2.5 m处,并在1.2 m处通过电子仪器测得小勇脚离地面的高度为0.624 m.
①求小勇跳到最高处时脚离地面的高度;
第2题图
解得b=-2.5m,
∴新抛物线的表达式为y=mx2-2.5mx,
∵抛物线经过点(1.2,0.624),
将(1.2,0.624)代入y=mx2-2.5mx中,解得m=-0.4,
∴y=-0.4x2+x,其顶点为(1.25,0.625),
则小勇跳到最高处时脚离地面的高度为0.625 m;
第2题图
②若男生立定跳远及格线为185 cm,求小勇在立定跳远过程中到及格线时脚离地面的高度.
第2题图
②∵185 cm=1.85 m,将x=1.85代入y=-0.4x2+x中,
得y=-0.4×1.852+1.85=0.481 m,
∴小勇在立定跳远过程中到及格线时
脚离地面的高度为0.481 m.
3. 根据以下素材,探索完成任务
如何设计隧道的限高方案 素材1 如图①是一个横断面呈抛物线形状的公路隧道口,经测量,其高度PH为8米,宽度OA为16米,图②是其示意图.
素材2 此隧道可双向通行,规定车辆在驶入隧道时,必须根据行车方向在隧道的中心线右侧、距离路边缘2米(AB=2米)这一范围内行驶,并保持车辆顶部与隧道的最小空隙不少于 米.
为了保证车辆的行驶安全,隧道下方需要设置
限高标志以警示车辆驾驶员.
第3题图
(1)确定隧道形状:在图中建立合适的平面直角坐标系,求抛物线的函数表达式;
第3题图②
解:(1)如图,以O为原点,以OA所在直线为x轴,以垂直于OA的直线为y轴建立平面直角坐标系,
x/米
y/米
由题意得,顶点P的坐标为(8,8),
∴设抛物线的函数表达式为y=a(x-8)2+8(a≠0).
又∵图象经过原点(0,0),∴0=a(0-8)2+8,
∴a=- ,∴抛物线的函数表达式为y=- (x-8)2+8,即y=- x2+2x;
(2)探究隧道限高方案:为使车辆按素材2的要求安全通过,求该隧道限高多少米?
(2)设该隧道限高h米,
∵OA=16,AB=2,∴OB=14,
当车高h一定,x=14时,车辆顶部与隧道的空隙最小,
此时,y=- ×(14-8)2+8= ,
此时,车辆顶部与隧道的最小空隙= -h,
由题意,车辆顶部与隧道的最小空隙= -h≥ ,
∴h≤3.∴该隧道限高3米;
第3题图②
x/米
y/米
(3)尝试隧道设计:在隧道中心线两侧的抛物线形拱壁上需要安装两排灯,使它们离地面的高度均相等且不超过6米,求两排灯的水平距离最小值.
(3)由题意,当y=6时,- (x-8)2+8=6,
解得x1=4,x2=12,∴x2-x1=8,
∴两排灯的水平距离最小值是8米.
第3题图②
x/米
y/米
4. 如图,一游乐场大门的截面图是由抛物线ADB和矩形OABC构成,矩形的边OA= 米,以OC所在直线为x轴,以OA所在直线为y轴建立平面直角坐标系xOy ,抛物线的顶点D的坐标为(4, ).
(1)求此抛物线对应的函数表达式;
第4题图
解:(1)由题意知,A(0, ),
抛物线顶点D的坐标为(4, ),
设抛物线的表达式为y=a(x-4)2+ ,
将点A(0, )代入得,
=a(0-4)2+ ,
解得a=- ,
∴抛物线对应的函数表达式为y=- (x-4)2+ ;
第4题图
(2)近期需对大门进行重新粉刷,工人师傅搭建一木板OE,点E正好在抛物线上,木板的支撑EG⊥x轴,OG=7米.一工人师傅站在木板OE上,他能刷到的最大垂直高度是 米,求大门顶部工人师傅没法刷到的区域对应的横坐标范围.
第4题图
(2)将x=7代入y=- (x-4)2+ 中,
得y=- ×(7-4)2+ = ,
∴点E(7, ),
∴设直线OE的表达式为y=kx(k≠0),
将点E(7, )代入得, =7k,
解得k= ,
∴直线OE的表达式为y= x,
如图,设M为抛物线上一点,点M的横坐标为m,过点M作y轴的平行线,交OE于点N.
第4题图
M
N
则MN=yM-yN=- (m-4)2+ - m
=- m2+ m+ =- (m- )2+ ,
∵师傅能刷到的最大垂直高度是 米,
∴当MN> 米时他就不能刷到大门顶部,
令MN= ,
即- (m- )2+ = ,
解得m1= ,m2=1,
又∵MN是关于m的二次函数,且图象开口向下,
∴工人师傅没法刷到的区域对应的横坐标范围是
1<m< .
第4题图
M
N
真实问题情境
题型一
文件解读
考情及趋势分析
教育部 2019年11 月发布的《关于加强初中学业水平考试命题工作的意见》和 2022年版《义务教育数学课程标准》中均指出:情境创设的真实性.
考情分析 年份 题号 题型 分值 情境 设问
2023 (10次) 2 选择题 3 实物背景北宋时期的汝官窑天蓝釉刻花鹅颈瓶 关于三视图说法正确的是
8 选择题 3 实际问题(七、八年级选择电影观看) 两个年级选择影片相同的概率
11 填空题 3 某校给每个年级配发劳动工具 3个年级需要配发多少套劳动工具
考情分析 年份 题号 题型 分值 情境 设问
2023(10次) 13 填空题 3 探究“无絮杨”品种苗的生长规律 估计不低于300 cm的“无絮杨”品种有多少棵
17 解答题 9 从甲、乙两家快递公司选一家合作配送樱桃 (1)填空:中位数的计算、方差的大小比较;(2)(3)开放性设问
19 解答题 9 小军借助反比例函数设计“鱼形”图案 (1)求k的值;(2)求扇形半径和圆心角度数;(3)直接写出阴影部分的面积之和
20 解答题 9 用自制的测高仪测树高 求树的高度
考情分析 年份 题号 题型 分值 情境 设问
2023(10次) 21 解答题 9 购买健身器材的优惠活动 (1)一定条件下的最优方案选择;(2)两种活动付款金额相等求原价;(3)一定条件下求原价的取值范围
22 解答题 10 羽毛球的击球路线 (1)求点P的坐标和字母的值;(2)计算一定条件下的方案选择
23 解答题 10 以“图形的变化”为主题设计的问题 (1)旋转角度,平移距离;(2)①判断两个角度的数量关系,②两点的距离;(3)一定条件下求线段长
2022(9次) 7 选择题 3 课后延时服务打分 所打分数的众数为
10 选择题 3 呼气式酒精测试仪 下列说法不正确的是
考情分析 年份 题号 题型 分值 情境 设问
2022(9次) 13 填空题 3 实际问题(选取两名宣讲员) 恰好选中甲和丙的概率
17 解答题 9 航空航天知识掌握情况 (1)填空:中位数的计算、百分比;(2)考查中位数的意义;(3)开放性设问
19 解答题 9 开封清明上河园拂云阁 求拂云阁的高度
20 解答题 9 让学生体验农耕劳动 (1)菜苗单价;(2)购买最少花费
21 解答题 9 喷水景观 (1)抛物线表达式;(2)小红与爸爸的水平距离
22 解答题 10 滚铁环 (1)求证两角之和等于90°;(2)一定条件下求线段长
考情分析 年份 题号 题型 分值 情境 设问
2022(9次) 23 解答题 10 以“矩形的折叠”为主题展开数学活动 (1)写出30°的角;(2)①求角度;②角之间的数量关系;(3)一定条件下求线段长
2021(7次) 8 选择题 3 卡片(北斗、天问、高铁、九章) 恰好选中天问和九章的概率
13 填空题 3 甲、乙两个厂家提供货源 更符合规格要求的厂家
15 填空题 3 小华用一张直角三角形纸片玩折纸游戏 求线段的长
17 解答题 9 了解学生睡眠时间情况 (1)填空:中位数的计算、百分比;(2)开放性设问
考情分析 年份 题号 题型 分值 情境 设问
2021(7次) 19 解答题 9 龙门石窟卢舍那佛像 求佛像的高度
20 解答题 9 “石磨原理”跨物理学科“连杆” (1)证明两个角的倍数关系;(2)求线段长
21 解答题 9 在网店购买A,B两款猕猴玩偶 (1)购进玩偶个数;(2)设计进货方案获得最大利润;(3)根据利润率判断哪次购买更合算
2020(6次) 8 选择题 3 我国快递业务2017年至2019年收入 可列方程为
17 解答题 9 山药粉加工厂对甲、乙两台不同品牌分装机的选择 (1)填空:中位数的计算、不合格率;(2)方差的意义
考情分析 年份 题号 题型 分值 情境 设问
2020(6次) 18 解答题 9 观星台 (1)求观星台最高点距离地面的高度;(2)提减少误差的建议
19 解答题 9 健身房暑期优惠活动 (1)(2)考查函数关系式并说明实际意义;(3)选取哪种方案所需费用最少
2020(6次) 20 解答题 9 “三分角器”的原理与使用方法的材料阅读 补充已知条件和求证
22 解答题 10 小亮遇到问题结合学习函数的经验研究问题 (1)①补充表中的值;②对得到的结论说明理由;(2)画图;(3)一定条件下求线段长
命题趋势·新考法分析
从2019年全国政策文件中提到关于真实问题情境(包含生活情境、科学情境、文化情境、数学情境),河南试题就开始注重考查真实问题情景试题,通过研究近几年全国考查的真实问题情境类试题,情境可分为下面几类:1. 背景情境:也就是我们常说的扣帽子的形式,情境与解题无关(如2023山西10题);2. 应用情境:这类试题情境与设问、图形相关,联系紧密,但仅停留在数学问题上(如2023北京21题);3. 实践应用:该类试题情境与设问强关联,且设问的提出、模型的构成均是来源于现实生活,且对现实生活具有一定的指导价值(如2023河南22题 ,2023甘肃省卷22题,2023舟山22题).从河南的中招考试分析,我们更应该关注第三类——实践应用的试题,真实情境试题设问回归情境,提出与情境关联性强,且具有实际意义,利用已有的数学知识或创造性的方法解决问题.将所得的数学答案放回真实情境之中,结合实际情况可判断答案是否符合实际或令人满意,反思是否还存在其他可能.
类型一 圆的实际应用(近4年3考)
1. (2023河南定心卷)蜗牛拖拉车(如图①)是一款休闲类玩具.如图②是小华为弟弟自制的一款蜗牛拖拉车,AB,BC为蜗牛的头和身体,蜗牛壳⊙O与BC相切于点B,连接OA,OB,OC,当小华弟弟从点D处拉蜗牛头部的绳子时,D,A,B三点共线,且AO∥BC,点E为CB延长线上一点,∠ABE=∠OCB.
(1)求证:AB=OC;
第1题图
(1)证明:∵∠ABE=∠OCB,
∴AB∥OC,
又∵AO∥BC,
∴四边形ABCO为平行四边形,
∴AB=OC;
第1题图
(2)若OB=5 cm,BC=12 cm,点D到点B的水平距离为132 cm,求绳子AD的长度.
第1题图
(2)解:如图,过点D作DF⊥BC交CB的延长线于点F,
∟
F
∵BC为⊙O的切线,
∴∠OBC=90°,
在Rt△OBC中,
OC= =13,
∵∠ABE=∠OCB,
∴△DFB∽△OBC,
∴ ,
即 ,
解得DB=143,
由(1)得AB=OC=13,
∴AD=DB-AB=143-13=130 cm.
第1题图
∟
F
2. (2023河南定心卷)如图①,太阳能热水器是指利用阳光中蕴含的能量将水加温的设备,属于可再生能源技术的一种.小明画出了热水器的示意图如图②所示,圆为水箱,AB为集热板,CD,AE为支架,CD垂直于屋面BC,延长BA与CD的延长线恰好交于圆上一点F,AE与圆相切于点A,经测量∠AEF=∠B.
(1)求证:BF过圆的圆心;
第2题图
(1)证明:由题意可知∠C=90°,
∴∠B+∠BFC=90°,
∵∠AEF=∠B,
∴∠AEF+∠BFC=90°,
∴∠FAE=90°,
∵AE是圆的切线,切点为A,
∴FA是圆的直径,
∴BF过圆的圆心;
第2题图
(2)若经测量热水器水箱直径长60 cm,∠B=60°,CD=136 cm,求热水器高度.
第2题图
(2)解:如图,连接AD,取AF的中点为点O,过点O分别作OH⊥BC于点H并交AD于点P,OG⊥FC交FC于点G,
O
∟
G
∟
H
P
则四边形OGCH为矩形,
∵CD=136,
∴PH=136,
∵AF为⊙O的直径,
∴∠ADF=90°,
∵∠C=90°,
∴AD∥BC,
∴∠FAD=∠B,
∵∠B=60°,
∴sin∠FAD=sinB= ,
即 ,
∵AF=60,
∴FD=30 ,OA=30,
第2题图
O
∟
G
∟
H
P
∵OH⊥BC,AD∥BC,
∴∠OPA=∠OHB=90°,
∵∠OAP=∠FAD,
∴△OAP∽△FAD,
∴ ,
∴OP=15 ,
∴热水器的高度为30+15 +136=(166+15 )cm.
第2题图
O
∟
G
∟
H
P
3. 如图①,过山车是一种机动游乐设施,常见于游乐园和主题乐园中,深受许多年轻游客的喜爱.如图②,过山车的轨道近似看成⊙O ,轨道的支撑AB,CD均与地面BC垂直,且与相切,点E为CD上一点,连接AE交⊙O 于点F,连接DF并延长与BC交于点G.已知AB=AD.
(1)求证:△ADE≌△DCG;
第3题图
(1)证明:∵AB,CD均与地面BC垂直,
且与⊙O相切,
∴∠ADE=∠DCG=∠ABC=∠BAD=90°,
∴四边形ABCD为矩形,∠ADF+∠CDG=90°,
∴AB=CD,
∵点F在⊙O上,AD为⊙O的直径,
∴∠AFD=90°,
∴∠DAE+∠ADF=90°,
∴∠CDG=∠DAE,
∵AB=AD,
∴AD=CD,
在△ADE与△DCG中,
第3题图
∴△ADE≌△DCG(ASA);
第3题图
(2)若DE=2 ,⊙O的半径为3,求AF的长.
第3题图
(2)解:由(1)知∠ADE=90°,∠AFD=90°,
∵DE=2 ,⊙O的半径为3,
∴AD=6,
在Rt△ADE中,
由勾股定理得AE= ,
在△ADE中,
根据三角形面积公式可知
AD·DE= AE·DF,
∴DF= =3,
∴在Rt△ADF中,
由勾股定理得AF= .
第3题图
4. (2023河南黑白卷)如图①是少年宫科技发明小组制作的一个钟表,钟面的大小会随时间的变化而发生改变.钟表底座为两根金属滑槽MN和GH,且MN⊥GH交于点O,钟面由若干个形如菱形ABCD的可活动木条组成,指针OP绕点O转动,菱形的顶点点B与点P用连杆连接.如图②,⊙O为P点的运动轨迹,⊙O与OH交于点E,连接PE,当BP与⊙O相切时,点A,B,P恰好在同一条直线上.
请仅就图②的情形解答下列问题:
第4题图
(1)求证:∠PBO+2∠PEO=90°;
第4题图
(1)证明:如图,连接OP,
∵BP与⊙O相切,
∴OP⊥BP,
∴∠PBO+∠BOP=90°,
∵OP=OE,
∴∠OPE=∠PEO,
∴∠BOP=∠OPE+∠PEO=2∠PEO,
∴∠PBO+2∠PEO=90°;
(2)若AB=OE=3,BP=4,求OD的长.
第4题图②
(2)解:在Rt△BOP中,OB= =5.
如图,过点A作AQ⊥BD于点Q,
∟
Q
∵四边形ABCD为菱形,
∴BD=2BQ,
∵AQ⊥BD,
∴∠AQB=90°,
∵∠ABQ=∠OBP,
由(1)知∠BPO=90°,
∴∠AQB=∠BPO=90°,
∴△ABQ∽△OBP,
∴ ,
∴BQ= ,
∴BD=2BQ= ,
∴OD=OB+BD=5+ = .
第4题图②
∟
Q
类型二 几何测量问题(9年9考)
1. 某数学兴趣小组计划测量学校教学楼的高度,他们在阳光下进行测量,如图,是同一时刻测量活动场景抽象出的平面几何图形,教学楼AB的影长为65 m,在教学楼影子末端点C处放着测角仪CD,CD的长为1.5 m,测角仪的影长CE为2. 3 m,且
AB EC,CD LEC,点B,C,E在同一直线
上,求教学楼的高度(结果保留整数).
⊥
⊥
第1题图
解:由题意得∠ABC=∠DCE=90°,AC∥DE,
∴∠ACB=∠DEC,
∴△ACB∽△DEC,
∴ ,
∴ ,
∴AB≈42(m),
答:教学楼的高度约为42 m.
第1题图
2. 如图①,中原大佛,位于河南省平顶山市鲁山县赵村乡上汤村佛泉寺,是世界上最高的佛教造像。某数学活动小组在学习完“锐角三角函数”之后,决定测量中原大佛的高度。为了减小误差,该数学活动小组在测量仰角的度数以及两个测量点之间的距离时,都分别测量了两次并取它们的平均值作为测量结果,测量数据如下
表(不完整):
第2题图①
活动课题 测量中原大佛的高度 活动工具 测角仪和皮尺 测量 示意图 说明:如图②,AB是中原大佛的截面图,他们先在点C处用高为1.5 m的测角仪CE测得塔顶点A的仰角∠AEF的度数,然后沿CB向D处前进,到达点D后用同样的测角仪从点D处测得点A的仰角∠AFG的度数,CD之间的距离可以直接测得,且点A,B,C,D,E,F,G在同一竖直平面内
第2题图①
第2题图②
测量 数据 测量项目 第一次 第二次 平均值
∠AEF 39.8° 40.2° 40°
∠AFG 44.7° 45.3° 45°
C,D之间 的距离 39.2 m 39.4 m ____ m
… (1)两次测量C,D之间的距离的平均值是__________m;
39.3
第2题图②
(2)根据以上测量结果,请你帮助该数学活动小组计算中原大佛AB的高度.(结果精确到1 m,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
(2)由题意得CE⊥CB,DF⊥CB,AB⊥CB,四边形EFDC为矩形,∠AEF=40°,∠AFG=45°,CD=EF=39.3 m,
∵∠AFG=45°,∴AG=FG.
设AG=FG=x,则EG=(x+39.3)m.
在Rt△AEG中,tan∠AEF=tan40°= ≈0.84,
解得x≈206.3.
第2题图②
经检验,x=206.3是原分式方程的解.
∴AB=AG+BG=206.3+1.5≈208(m).
答:中原大佛AB的高度约为208 m.
第2题图②
3. 小明利用所学知识来测量操场上的一个照明灯的高度.如图所示,矩形PDCQ为照明灯AB一侧观礼台的竖直截面示意图,他先到观礼台底部点C处,用测角仪CE测得照明灯顶端点A的仰角为45°,再在平台上点D处放置一个平面镜,在距平面镜1.7 m 的点G处恰好看到照明灯顶端点A,此时小明眼睛到观礼台的高度FG为1.6 m,
其中点Q,C,B在同一直线上,AB BC, FG DG,
EC BC.已知测角仪CE的高度为1.5 m,观礼台CD
的高度为2 m,求照明灯的高AB.(平面镜的大小,
测角仪的宽度忽略不计)
⊥
⊥
⊥
第3题图
第3题图
解:如图,分别过点D,E作AB的垂线,垂足分别为M,N,
∟
M
∟
N
∵AB⊥BC,四边形PQCD为矩形,
∴DC⊥BC,
∴四边形DMNE,四边形ENBC均为矩形,
∴DM=EN=CB,CE=BN,DE=MN,
∵∠AEN=45°,
∴EN=AN,
设DM=x,则CB=EN=AN=x,
∵DC=2,CE=1.5,
∴MN=DE=DC-EC=0.5,
∴AM=AN-MN=x-0.5,
由平面镜反射可得,∠FDG=∠ADM,
∵∠FGD=∠AMD=90°,
∴△ADM∽△FDG,
∴ ,即 ,解得x=8.5,
第3题图
∟
M
∟
N
∴AB=8.5+1.5=10,
答:照明灯的高AB为10 m.
4. (2023河南定心卷)2023年3月15日新晋高速公路全线通车,从陵川县到河南省新乡市也将从过去的3个多小时缩短至1个多小时,沿线共11座隧道.如图①,前期开挖其中一条隧道时,为了估算工程量,需要测量山两端AB的长,如图②,在山外一点C处测得点A位于点C的西北方向,点B位于点C的北偏东37°方向,并测得AC的距离为141 m,BC的距离为500 m,求山两端AB的长(结果精确到1 m,
参考数据:sin37°≈0.60,cos37°≈0.80,
tan37°≈0.75, ≈1.41).
第4题图
第4题图②
解:如图,过点C作东西方向水平线DE,过点A作AD⊥DE于点D,过点B作BE⊥DE于点E,
D
E
∟
∟
由题意可知,∠ACD=45°,∠CBE=37°,AC=141,BC=500,
在Rt△ACD中,sin∠ACD= ,cos∠ACD= ,
∴AC= = CD= AD=141≈100 ,
∴CD=AD≈100,
在Rt△BCE中,sin∠CBE= ,
cos∠CBE= ,
∴CE=BC·sin∠CBE=500sin37°,
BE=BC·cos∠CBE=500cos37°,
过点A作AF⊥BE交BE于点F,
第4题图②
D
E
∟
∟
∟
F
∴四边形ADEF为矩形,
∴AF=DE,AD=EF,
在Rt△ABF中,
AB=
≈500 m.
答:山两端AB的长约为500 m.
类型三 抛物线型的实际应用(近2年连续考查)
1. (2023河南黑白卷)如图①,一小球从静止沿斜坡下滑,小球离开桌面时做平抛运动(不考虑空气阻力),用频闪照相机观测到小球运动过程中的几个位置,并用平滑曲线连接得到小球平抛运动的轨迹.如图②,以小球滚出桌面的水平方向为x轴正方向,竖直向上方向为y轴正方向,小球离开桌面的位置为原点建立平面直角坐标系(小球的体积忽略不计),得到小球的位置坐标(x,y),根据平抛运动可知x,y与时
间t的关系如下: 已知桌面的高度为100
厘米,观测到三个时刻小球的位置坐标如下表:
第1题图
t(秒) 1 2 3
x(厘米) 10 20 30
y(厘米) -5 -20 -45
(1)求v和g的值;
第1题图
解:(1)∵x=vt,
∴将(1,10)代入x=vt中,得v=10,
∵y=- gt2,
∴将(1,-5)代入y=- gt2中,得g=10,
∴v=10,g=10;
(2)求小球做平抛运动时,运动轨迹所形成的抛物线的解析式;
第1题图
(2)∵v=10,g=10,
∴x=10t,y=-5t2,
∴y关于x的解析式,
即做平抛运动的运动轨迹所形成的
抛物线解析式为y=- ;
(3)小球水平抛出的正前方有一高为20厘米的正方体纸箱(纸箱厚度忽略不计),若要使小球落入纸箱中,求纸箱左侧到桌子的水平距离L的取值范围.
第1题图
(3)∵桌面的高度为100厘米,正方体纸箱的高度为20厘米,小球要落入纸箱,则小球要在y=-80时进入纸箱,
∴将y=-80代入y=- ,解得x=40(负值已舍去),
∵正方体纸箱的高度为20厘米,
∴纸箱左侧到桌子的最短水平距离
为40-20=20(厘米),
∴纸箱到桌子的水平距离L的取值范围为
20厘米<L<40厘米.
2. (2023河南定心卷)中考体育考试规定男生立定跳远满分为2.5 m,如图①,小勇立定跳远为2.4 m,小聪发现小勇立定跳远时脚的运动轨迹可近似看作抛物线,通过电子仪器测量得到小勇跳远时脚离地面的最高距离为72 cm,如图②,以小勇起跳点为原点建立平面直角坐标系,小勇落地点为A,最高点为B.
第2题图
(1)求小勇跳远时抛物线的表达式;
第2题图
解:(1)设抛物线的表达式为y=a(x-h)2+k(a≠0),
由题意知,点B(1.2,0.72)是抛物线的顶点,
∴y=a(x-1.2)2+0.72,
又∵抛物线经过点A(2.4,0),
∴0=a(2.4-1.2)2+0.72,
解得a=-0.5,
∴抛物线的表达式为y=-0.5(x-1.2)2+0.72
(或y=-0.5x2+1.2x);
(2)①由题意知,
小勇调整跳远姿势后新抛物线过原点(0,0),
∴设新抛物线表达式为y=mx2+bx,
∵抛物线经过点(2.5,0),
把(2.5,0)代入y=mx2+bx中,
(2)体育老师告诉小勇他的跳远姿势不对,调整跳远姿势后,小勇恰好跳到了2.5 m处,并在1.2 m处通过电子仪器测得小勇脚离地面的高度为0.624 m.
①求小勇跳到最高处时脚离地面的高度;
第2题图
解得b=-2.5m,
∴新抛物线的表达式为y=mx2-2.5mx,
∵抛物线经过点(1.2,0.624),
将(1.2,0.624)代入y=mx2-2.5mx中,解得m=-0.4,
∴y=-0.4x2+x,其顶点为(1.25,0.625),
则小勇跳到最高处时脚离地面的高度为0.625 m;
第2题图
②若男生立定跳远及格线为185 cm,求小勇在立定跳远过程中到及格线时脚离地面的高度.
第2题图
②∵185 cm=1.85 m,将x=1.85代入y=-0.4x2+x中,
得y=-0.4×1.852+1.85=0.481 m,
∴小勇在立定跳远过程中到及格线时
脚离地面的高度为0.481 m.
3. 根据以下素材,探索完成任务
如何设计隧道的限高方案 素材1 如图①是一个横断面呈抛物线形状的公路隧道口,经测量,其高度PH为8米,宽度OA为16米,图②是其示意图.
素材2 此隧道可双向通行,规定车辆在驶入隧道时,必须根据行车方向在隧道的中心线右侧、距离路边缘2米(AB=2米)这一范围内行驶,并保持车辆顶部与隧道的最小空隙不少于 米.
为了保证车辆的行驶安全,隧道下方需要设置
限高标志以警示车辆驾驶员.
第3题图
(1)确定隧道形状:在图中建立合适的平面直角坐标系,求抛物线的函数表达式;
第3题图②
解:(1)如图,以O为原点,以OA所在直线为x轴,以垂直于OA的直线为y轴建立平面直角坐标系,
x/米
y/米
由题意得,顶点P的坐标为(8,8),
∴设抛物线的函数表达式为y=a(x-8)2+8(a≠0).
又∵图象经过原点(0,0),∴0=a(0-8)2+8,
∴a=- ,∴抛物线的函数表达式为y=- (x-8)2+8,即y=- x2+2x;
(2)探究隧道限高方案:为使车辆按素材2的要求安全通过,求该隧道限高多少米?
(2)设该隧道限高h米,
∵OA=16,AB=2,∴OB=14,
当车高h一定,x=14时,车辆顶部与隧道的空隙最小,
此时,y=- ×(14-8)2+8= ,
此时,车辆顶部与隧道的最小空隙= -h,
由题意,车辆顶部与隧道的最小空隙= -h≥ ,
∴h≤3.∴该隧道限高3米;
第3题图②
x/米
y/米
(3)尝试隧道设计:在隧道中心线两侧的抛物线形拱壁上需要安装两排灯,使它们离地面的高度均相等且不超过6米,求两排灯的水平距离最小值.
(3)由题意,当y=6时,- (x-8)2+8=6,
解得x1=4,x2=12,∴x2-x1=8,
∴两排灯的水平距离最小值是8米.
第3题图②
x/米
y/米
4. 如图,一游乐场大门的截面图是由抛物线ADB和矩形OABC构成,矩形的边OA= 米,以OC所在直线为x轴,以OA所在直线为y轴建立平面直角坐标系xOy ,抛物线的顶点D的坐标为(4, ).
(1)求此抛物线对应的函数表达式;
第4题图
解:(1)由题意知,A(0, ),
抛物线顶点D的坐标为(4, ),
设抛物线的表达式为y=a(x-4)2+ ,
将点A(0, )代入得,
=a(0-4)2+ ,
解得a=- ,
∴抛物线对应的函数表达式为y=- (x-4)2+ ;
第4题图
(2)近期需对大门进行重新粉刷,工人师傅搭建一木板OE,点E正好在抛物线上,木板的支撑EG⊥x轴,OG=7米.一工人师傅站在木板OE上,他能刷到的最大垂直高度是 米,求大门顶部工人师傅没法刷到的区域对应的横坐标范围.
第4题图
(2)将x=7代入y=- (x-4)2+ 中,
得y=- ×(7-4)2+ = ,
∴点E(7, ),
∴设直线OE的表达式为y=kx(k≠0),
将点E(7, )代入得, =7k,
解得k= ,
∴直线OE的表达式为y= x,
如图,设M为抛物线上一点,点M的横坐标为m,过点M作y轴的平行线,交OE于点N.
第4题图
M
N
则MN=yM-yN=- (m-4)2+ - m
=- m2+ m+ =- (m- )2+ ,
∵师傅能刷到的最大垂直高度是 米,
∴当MN> 米时他就不能刷到大门顶部,
令MN= ,
即- (m- )2+ = ,
解得m1= ,m2=1,
又∵MN是关于m的二次函数,且图象开口向下,
∴工人师傅没法刷到的区域对应的横坐标范围是
1<m< .
第4题图
M
N
同课章节目录
