4.5.1函数的零点及其方程的解 课件(共17张PPT)
文档属性
| 名称 | 4.5.1函数的零点及其方程的解 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 681.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-28 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
4.5.1函数的零点与方程的解
虽然今天我们可以从教科书中了解各式各样方程的解法,但这一切却经历了相当漫长的岁月.引语:在人类用智慧架设的无数座从未知通向已知的金桥中,方程的求解是其中璀璨的一座.
约公元50-100年编成的《九章算术》给出了一次方程、二次方程和正系数三次方程的求解方法.
问题2:求方程
的解。
的图像,并求出函数的零点。
问题3:画出函数
新知探索
问题1:求方程-5x+4=0的解。
零点:
对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点.
函数的零点是一个点吗?
问题4:
零点不是一个点,零点指的是一个实数.
问题5:上述定义蕴含了怎样的等价关系?
函数有零点
函数图象与轴相交的横坐标
方程f(x)=0有实数解
数
形
由此可知,求方程f(x)=0的实数解,就是确定函数y=f(x)的零点.
例1:判断下列函数是否存在零点,如果存在,请求出.(1) f (x)=x(x+3);
(2) f (x)=x2+2x+4;
新知探索
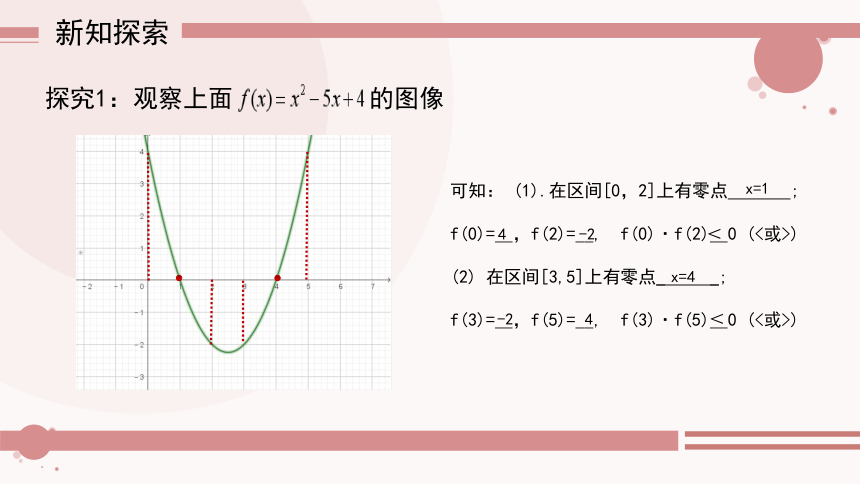
可知: (1).在区间[0,2]上有零点 ;
f(0)=__,f(2)=__, f(0)·f(2)__0 (<或>)
(2) 在区间[3,5]上有零点_ _;
f(3)=__,f(5)=__, f(3)·f(5)__0 (<或>)
探究1:观察上面
的图像
4
-2
<
-2
4
<
x=1
x=4
探究二:如果函数 y=f(x) 在区间[a,b]上有 f(a)·f(b)<0,那么函数 y=f(x) 在区间 (a,b) 内是否一定有零点?
0
y
x
“在给定区间[a,b]上连续”和“f(a)·f(b)<0”这两个条件缺一不可
探究三:如果函数 y=f(x)在区间[a,b]上是连续不断的一条曲线,那么函数 y=f(x)在区间 (a,b) 内是否一定有零点?
0
y
x
1. 若函数 y=f(x)在区间[a,e]上有f(a)·f(e)<0,则函数f (x)在区间(a,e) 内至少有一个零点
新知探索
新知探索
2.函数 y=f(x)在区间[a,b]上的图象是一条连续不断的曲线,且有f(a)·f(b)>0,则函数f (x)在区间(a,b) 内有零点吗
新知探索
3.若函数 y=f(x)在区间[a,b]上的图像是连续不断的曲线,且有零点,则一定有f(a)·f(b)<0吗?
单调函数
0
y
x
4:什么情况下有唯一一个零点?
已知函数 y=f(x) 在区间[a,b]上的图象如下图,
则函数 y=f(x) 在区间[a,b]内有几个零点
五个
1
-1
-2
-1
2
1
0
3
2
1
-1
-1
2
1
0
例2 求方程的实数解的个数.
学以致用
小试牛刀
这节课你收获了什么?
4.5.1函数的零点与方程的解
虽然今天我们可以从教科书中了解各式各样方程的解法,但这一切却经历了相当漫长的岁月.引语:在人类用智慧架设的无数座从未知通向已知的金桥中,方程的求解是其中璀璨的一座.
约公元50-100年编成的《九章算术》给出了一次方程、二次方程和正系数三次方程的求解方法.
问题2:求方程
的解。
的图像,并求出函数的零点。
问题3:画出函数
新知探索
问题1:求方程-5x+4=0的解。
零点:
对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点.
函数的零点是一个点吗?
问题4:
零点不是一个点,零点指的是一个实数.
问题5:上述定义蕴含了怎样的等价关系?
函数有零点
函数图象与轴相交的横坐标
方程f(x)=0有实数解
数
形
由此可知,求方程f(x)=0的实数解,就是确定函数y=f(x)的零点.
例1:判断下列函数是否存在零点,如果存在,请求出.(1) f (x)=x(x+3);
(2) f (x)=x2+2x+4;
新知探索
可知: (1).在区间[0,2]上有零点 ;
f(0)=__,f(2)=__, f(0)·f(2)__0 (<或>)
(2) 在区间[3,5]上有零点_ _;
f(3)=__,f(5)=__, f(3)·f(5)__0 (<或>)
探究1:观察上面
的图像
4
-2
<
-2
4
<
x=1
x=4
探究二:如果函数 y=f(x) 在区间[a,b]上有 f(a)·f(b)<0,那么函数 y=f(x) 在区间 (a,b) 内是否一定有零点?
0
y
x
“在给定区间[a,b]上连续”和“f(a)·f(b)<0”这两个条件缺一不可
探究三:如果函数 y=f(x)在区间[a,b]上是连续不断的一条曲线,那么函数 y=f(x)在区间 (a,b) 内是否一定有零点?
0
y
x
1. 若函数 y=f(x)在区间[a,e]上有f(a)·f(e)<0,则函数f (x)在区间(a,e) 内至少有一个零点
新知探索
新知探索
2.函数 y=f(x)在区间[a,b]上的图象是一条连续不断的曲线,且有f(a)·f(b)>0,则函数f (x)在区间(a,b) 内有零点吗
新知探索
3.若函数 y=f(x)在区间[a,b]上的图像是连续不断的曲线,且有零点,则一定有f(a)·f(b)<0吗?
单调函数
0
y
x
4:什么情况下有唯一一个零点?
已知函数 y=f(x) 在区间[a,b]上的图象如下图,
则函数 y=f(x) 在区间[a,b]内有几个零点
五个
1
-1
-2
-1
2
1
0
3
2
1
-1
-1
2
1
0
例2 求方程的实数解的个数.
学以致用
小试牛刀
这节课你收获了什么?
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
