人教版九年级数学上册第22章《二次函数》期末复习题 (6)(含答案)
文档属性
| 名称 | 人教版九年级数学上册第22章《二次函数》期末复习题 (6)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 198.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-28 16:25:10 | ||
图片预览


文档简介
九年级上册第22章《二次函数》期末复习题
一、选择题
1.下列各式中,y是x的二次函数的是( )
A.y=ax2+bx+c B.x2+y﹣2=0 C.y2﹣ax=﹣2 D.x2﹣y2+1=0
2.二次函数y=kx2-6x+3的图象与x轴有两个交点,则k的取值范围是( )
A.k<3 B.k<3 且k≠0 C.k ≤3 D.k ≤3且k≠0
3.若二次函数y=ax2+bx+c的顶点在第一象限,且经过点(0,1)、(-1,0),则y=a+b+c的取值范围是 ( )
A.y>1 B.-1<y<1 C.0<y<2 D.1<y<2
4.若二次函数y=ax2(a≠0)的图象经过点(﹣2,﹣1),则必在该图象上的点还有( )
A.(2,﹣1) B.(2,1)
C.(﹣1,﹣2) D.(﹣2,1)
5.已知二次函数y=x2﹣6x+m的图象过A(﹣3,a),B(0,b),C(5,c)三点,则a、b、c的大小关系是( )
A.c>b>a B.a>b>c C.a>c>b D.c>a>b
6.在二次函数y=﹣x2+2x+1的图象中,若y随x的增大而增大,则x的取值范围是( )
A.x>1 B.x<1 C.x>﹣1 D.x<﹣1
7.方程ax2+bx+c=0的两个根是-3和1,那么二次函数y=ax2+bx+c的图象的对称轴是直线( )
A.x=-3 B.x=-2 C.x=-1 D.x=1
二、填空题
8.如果 是二次函数,则m= .
9.二次函数y=x2﹣3x+2的图象与x轴的交点坐标是 ,与y轴的交点坐标为 .
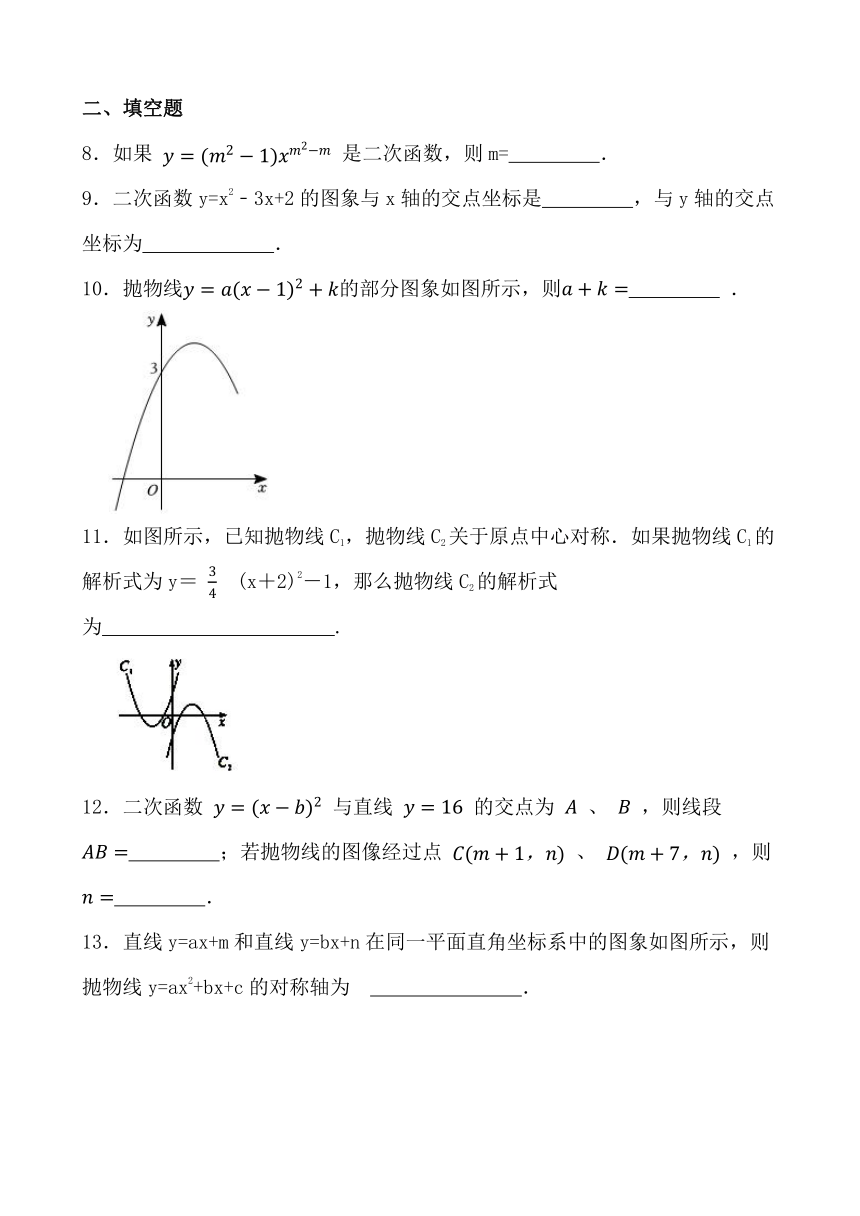
10.抛物线的部分图象如图所示,则 .
11.如图所示,已知抛物线C1,抛物线C2关于原点中心对称.如果抛物线C1的解析式为y= (x+2)2-1,那么抛物线C2的解析式为 .
12.二次函数 与直线 的交点为 、 ,则线段 ;若抛物线的图像经过点 、 ,则 .
13.直线y=ax+m和直线y=bx+n在同一平面直角坐标系中的图象如图所示,则抛物线y=ax2+bx+c的对称轴为
.
14.若二次函数 的对称轴为直线 ,则关于 的方程 的解为 .
15.如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,边OA在x轴正半轴上,点B、P都在函数y= (x>0)的图象上,过点P分别作x轴、y轴的平行线,交于点D、E.点P在点B的上方.若CD:CO=1:2,矩形OEFC的面积是 .
三、解答题
16.已知二次函数的图象的顶点坐标为(﹣2,﹣3),且图象过点(﹣3,﹣1),求这个二次函数的解析式.
17.有一抛物线拱桥,已知水位线在AB位置时,水面的宽为4 米,水位上升4米,就达到警戒线CD,这时水面宽为4 米.若洪水到来时,水位以每小时0.5米的速度上升,则水过警戒线后几小时淹没到拱桥顶端M处?
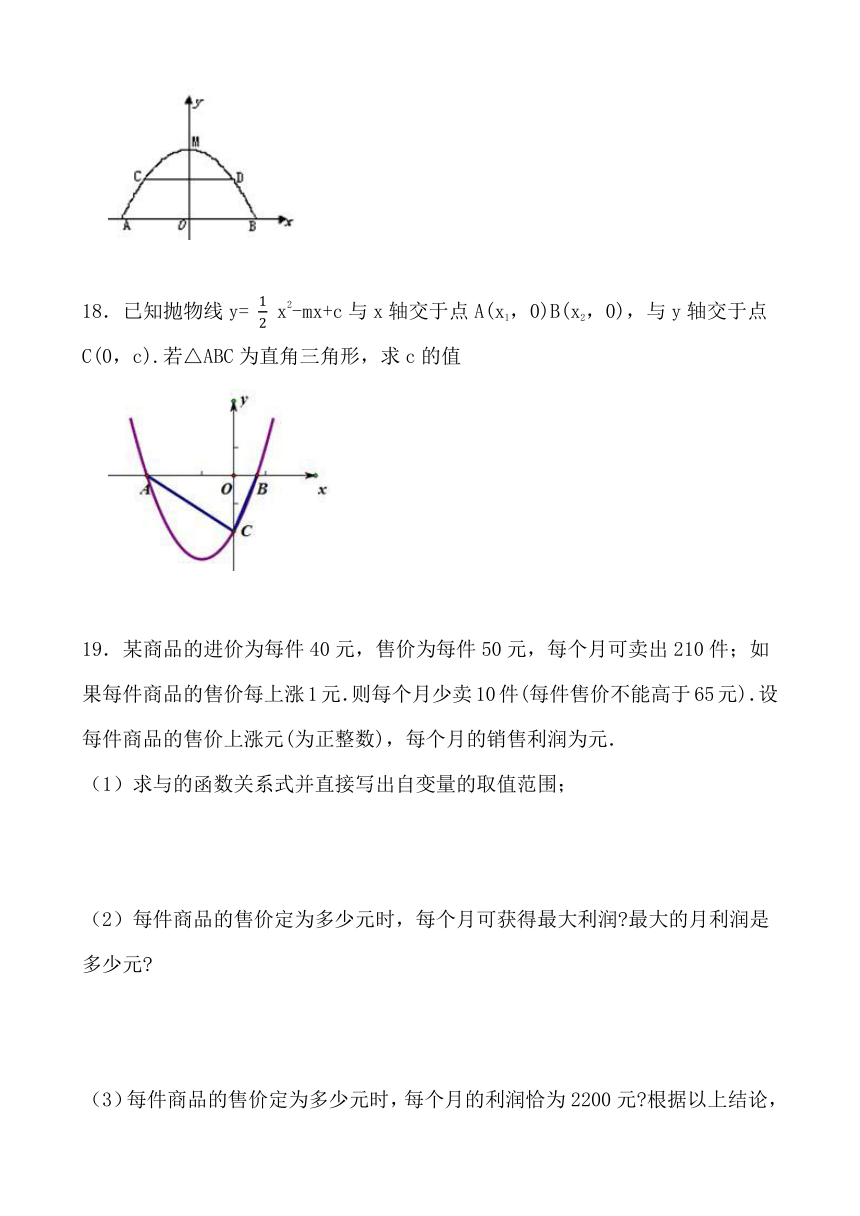
18.已知抛物线y= x2-mx+c与x轴交于点A(x1,0)B(x2,0),与y轴交于点C(0,c).若△ABC为直角三角形,求c的值
19.某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元.则每个月少卖10件(每件售价不能高于65元).设每件商品的售价上涨元(为正整数),每个月的销售利润为元.
(1)求与的函数关系式并直接写出自变量的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润 最大的月利润是多少元
(3)每件商品的售价定为多少元时,每个月的利润恰为2200元 根据以上结论,请你直接写出售价在什么范围时,每个月的利润不低于2200元
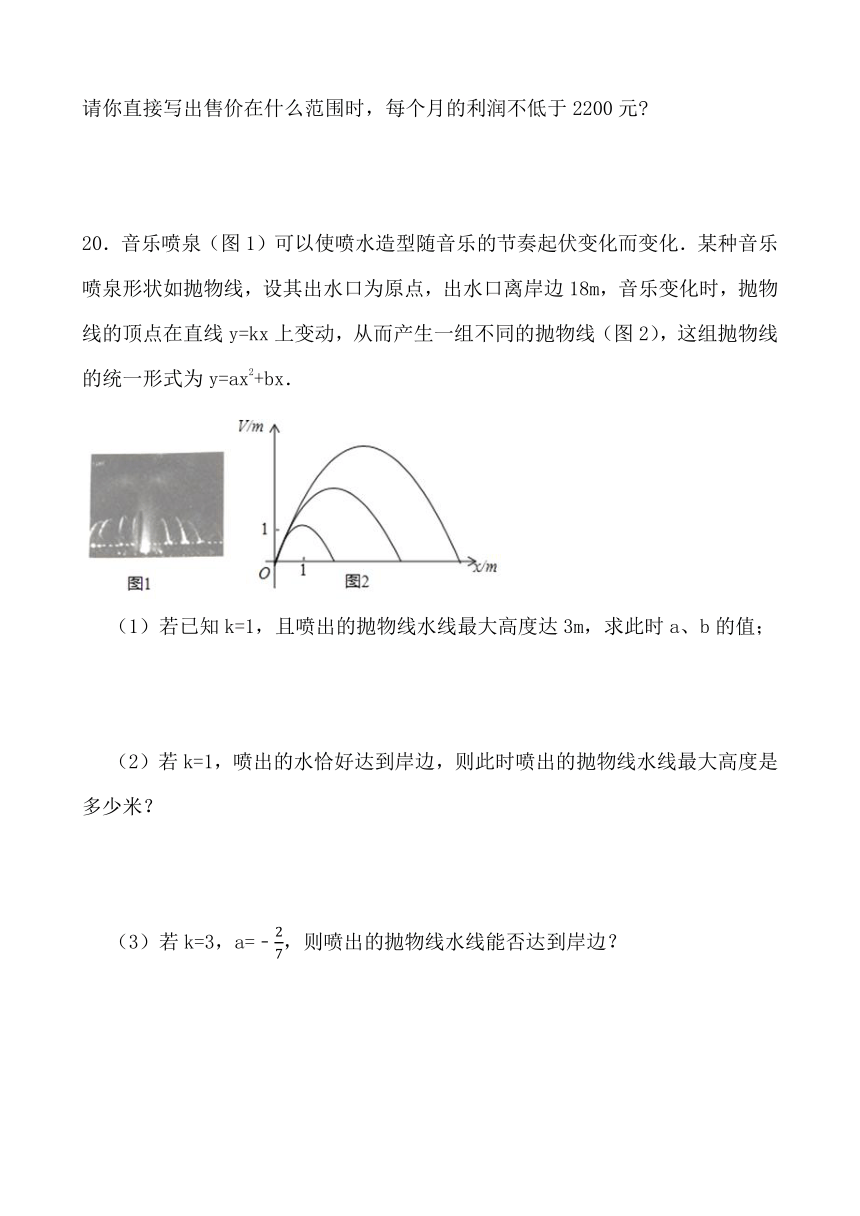
20.音乐喷泉(图1)可以使喷水造型随音乐的节奏起伏变化而变化.某种音乐喷泉形状如抛物线,设其出水口为原点,出水口离岸边18m,音乐变化时,抛物线的顶点在直线y=kx上变动,从而产生一组不同的抛物线(图2),这组抛物线的统一形式为y=ax2+bx.
(1)若已知k=1,且喷出的抛物线水线最大高度达3m,求此时a、b的值;
(2)若k=1,喷出的水恰好达到岸边,则此时喷出的抛物线水线最大高度是多少米?
(3)若k=3,a=﹣,则喷出的抛物线水线能否达到岸边?
21.如图所示,用一段长为30 m的篱笆围成一个一边靠墙(墙的长度不限)的矩形菜园ABCD,设AB边的长为.求:
(1)菜园的面积关于的函数表达式.
(2)自变量的取值范围.
22.如图,抛物线 交 轴于 两点,交 轴于点 , .
(1)求抛物线的解析式;
(2)若 是抛物线的第一象限图象上一点,设点 的横坐标为m,
点 在线段 上,CD=m,当 是以 为底边的等腰三角形时,求点 的坐标;
(3)在(2)的条件下,是否存在抛物线上一点 ,使 ,若存在,求出点 的坐标;若不存在,请说明理由.
答案解析部分
1.B
2.B
3.C
4.A
5.B
6.B
7.C
8.2
9.(1,0)、(2,0);(0,2)
10.3
11.y= (x-2)2+1
12.;
13.直线x=-
14. ,
15.
16.解 :设解析式为:y=a(x+2)2﹣3,
将(﹣3,﹣1)代入得出:﹣1=a(﹣3+2)2﹣3,
解得: a=2.
故这个二次函数的解析式为:y=2(x+2)2﹣3
17.解:∵AB=4 ,CD=4 ,
∴A(-2 ,0),B(2 ,0),C(-2 ,4),D(2 ,4),
设函数的解析式为y=a(x-2 )(x+2 ),由题意,得
4=a(2 -2 )(2 +2 ),
解得a=- ,
则y=- (x-2 )(x+2 )=- x2+8.
当x=0时,
y=8,
则OM=8.
则水过警戒线后淹没到拱桥顶端M处的时间为:(8-4)÷0.5=8小时.
答:水过警戒线后淹没到拱桥顶端M处的时间为8小时.
18.解:∵△ABC为直角三角形,
∴∠ACB=90°,
∵∠ACO+∠BCO=90°,∠CBO+∠BCO=90°,
∴∠ACO=∠CBO,
∴△ACO∽△CBO,
∴ ,
∴OC2=OB·OA.
当y=0时, x2-mx+c=0,
∴x1·x2=2c,
∴OB·OA=-2c.
∵C(0,c),
∴OC=-c,
∴(-c)2=-2c,
∴c2+2c=0,
∴c1=0(舍去),c2=-2.
∴c的值是-2.
19.解:(1)∵设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元.
∴上涨后每件商品的利润为(10+x)元,每月能销售(210﹣10x)件商品;
由题意得:y=(210﹣10x)(50+x﹣40)
=﹣10x2+110x+2100
=﹣10(x﹣5.5)2+2402.5(0<x≤15且x为整数);
(2)∵a=﹣10<0,
∴当x=5.5时,y有最大值2402.5.
∵0<x≤15,且x为整数,
当x=5时,50+x=55,y=2400(元),当x=6时,50+x=56,y=2400(元)
∴当售价定为每件55或56元,每个月的利润最大,最大的月利润是2400元;
(3)当y=2200时,﹣10x2+110x+2100=2200,
解得:x1=1,x2=10.
∴当x=1时,50+x=51,当x=10时,50+x=60.
∴当售价定为每件51或60元,每个月的利润为2200元.
当售价不低于51或60元,每个月的利润为2200元.
当售价不低于51元且不高于60元且为整数时,每个月的利润不低于2200元(或当售价分别为51,52,53,54,55,56,57,58,59,60元时,每个月的利润不低于2200元).
20.解:(1)∵y=ax2+bx的顶点为(﹣),抛物线的顶点在直线y=kx上,k=1,抛物线水线最大高度达3m,
∴,,
解得,a=,b=2,
即k=1,且喷出的抛物线水线最大高度达3m,此时a、b的值分别是,2;
(2)∵k=1,喷出的水恰好达到岸边,出水口离岸边18m,抛物线的顶点在直线y=kx上,
∴此时抛物线的对称轴为x=9,y=x=9,
即此时喷出的抛物线水线最大高度是9米;
(3)∵y=ax2+bx的顶点为(﹣)在直线y=3x上,a=﹣,
∴,
解得,b=6,
∴抛物线y=,
当y=0时,0=,
解得,x1=21,x2=0,
∵21>18,
∴若k=3,a=﹣,则喷出的抛物线水线能达到岸边,
即若k=3,a=﹣,喷出的抛物线水线能达到岸边.
21.(1)解:设AB的长为x(m),则AD的长为:(m),
由题意可得,;
(2)解:由于强的长度不限,
∴,
解得.
22.解:(Ⅰ) ∵当 =0时, =4,∴C(0,4) ,OB=4OA, CBO=45°∴OC=OB=4, OA=1 A(-1,0) ,B(4,0)设 ,解得: =-1,(Ⅱ) 设P(m,-m2+3m+4),PCD是以CD为底边的等腰三角形时,过点P作PE⊥CD于E,CD=m CE=DE,OE=4- m,∴4- m=-m2+3m+4 m>0 m= ∴P( , )(Ⅲ)假设存在,过点P作PE⊥CD于点E,且交CB于H,过点P作PF⊥AB于F,P( , )这时CD=3.5 ,D(0,0.5)可求出直线PD的解析式: 可知直线PD 过点A(-1,0)若设∠APQ2=∠BCP= ∠CPE=∠EPA=∠PAB= , CBO= CHE= 45°,又 CHE= + ∴ + =45°= EPG = PGF ∴PF=FG= ,OG= - = ∴G( ,0), 可求出直线PG的解析式: 由 解得x1 = ,x2= (舍去)∴ Q2( , )作点G关于直线AP的对称点S,由于PD的解析式: ∴设GS的解析式: 过点G,得出 = , ,联立得: ,解得:求出点K( , )∵点K为SG的中点,求出S( , ) P( , ) ∴PS的解析式为: ∴ ,解得: (舍去) , ,∴Q1( , )
一、选择题
1.下列各式中,y是x的二次函数的是( )
A.y=ax2+bx+c B.x2+y﹣2=0 C.y2﹣ax=﹣2 D.x2﹣y2+1=0
2.二次函数y=kx2-6x+3的图象与x轴有两个交点,则k的取值范围是( )
A.k<3 B.k<3 且k≠0 C.k ≤3 D.k ≤3且k≠0
3.若二次函数y=ax2+bx+c的顶点在第一象限,且经过点(0,1)、(-1,0),则y=a+b+c的取值范围是 ( )
A.y>1 B.-1<y<1 C.0<y<2 D.1<y<2
4.若二次函数y=ax2(a≠0)的图象经过点(﹣2,﹣1),则必在该图象上的点还有( )
A.(2,﹣1) B.(2,1)
C.(﹣1,﹣2) D.(﹣2,1)
5.已知二次函数y=x2﹣6x+m的图象过A(﹣3,a),B(0,b),C(5,c)三点,则a、b、c的大小关系是( )
A.c>b>a B.a>b>c C.a>c>b D.c>a>b
6.在二次函数y=﹣x2+2x+1的图象中,若y随x的增大而增大,则x的取值范围是( )
A.x>1 B.x<1 C.x>﹣1 D.x<﹣1
7.方程ax2+bx+c=0的两个根是-3和1,那么二次函数y=ax2+bx+c的图象的对称轴是直线( )
A.x=-3 B.x=-2 C.x=-1 D.x=1
二、填空题
8.如果 是二次函数,则m= .
9.二次函数y=x2﹣3x+2的图象与x轴的交点坐标是 ,与y轴的交点坐标为 .
10.抛物线的部分图象如图所示,则 .
11.如图所示,已知抛物线C1,抛物线C2关于原点中心对称.如果抛物线C1的解析式为y= (x+2)2-1,那么抛物线C2的解析式为 .
12.二次函数 与直线 的交点为 、 ,则线段 ;若抛物线的图像经过点 、 ,则 .
13.直线y=ax+m和直线y=bx+n在同一平面直角坐标系中的图象如图所示,则抛物线y=ax2+bx+c的对称轴为
.
14.若二次函数 的对称轴为直线 ,则关于 的方程 的解为 .
15.如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,边OA在x轴正半轴上,点B、P都在函数y= (x>0)的图象上,过点P分别作x轴、y轴的平行线,交于点D、E.点P在点B的上方.若CD:CO=1:2,矩形OEFC的面积是 .
三、解答题
16.已知二次函数的图象的顶点坐标为(﹣2,﹣3),且图象过点(﹣3,﹣1),求这个二次函数的解析式.
17.有一抛物线拱桥,已知水位线在AB位置时,水面的宽为4 米,水位上升4米,就达到警戒线CD,这时水面宽为4 米.若洪水到来时,水位以每小时0.5米的速度上升,则水过警戒线后几小时淹没到拱桥顶端M处?
18.已知抛物线y= x2-mx+c与x轴交于点A(x1,0)B(x2,0),与y轴交于点C(0,c).若△ABC为直角三角形,求c的值
19.某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元.则每个月少卖10件(每件售价不能高于65元).设每件商品的售价上涨元(为正整数),每个月的销售利润为元.
(1)求与的函数关系式并直接写出自变量的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润 最大的月利润是多少元
(3)每件商品的售价定为多少元时,每个月的利润恰为2200元 根据以上结论,请你直接写出售价在什么范围时,每个月的利润不低于2200元
20.音乐喷泉(图1)可以使喷水造型随音乐的节奏起伏变化而变化.某种音乐喷泉形状如抛物线,设其出水口为原点,出水口离岸边18m,音乐变化时,抛物线的顶点在直线y=kx上变动,从而产生一组不同的抛物线(图2),这组抛物线的统一形式为y=ax2+bx.
(1)若已知k=1,且喷出的抛物线水线最大高度达3m,求此时a、b的值;
(2)若k=1,喷出的水恰好达到岸边,则此时喷出的抛物线水线最大高度是多少米?
(3)若k=3,a=﹣,则喷出的抛物线水线能否达到岸边?
21.如图所示,用一段长为30 m的篱笆围成一个一边靠墙(墙的长度不限)的矩形菜园ABCD,设AB边的长为.求:
(1)菜园的面积关于的函数表达式.
(2)自变量的取值范围.
22.如图,抛物线 交 轴于 两点,交 轴于点 , .
(1)求抛物线的解析式;
(2)若 是抛物线的第一象限图象上一点,设点 的横坐标为m,
点 在线段 上,CD=m,当 是以 为底边的等腰三角形时,求点 的坐标;
(3)在(2)的条件下,是否存在抛物线上一点 ,使 ,若存在,求出点 的坐标;若不存在,请说明理由.
答案解析部分
1.B
2.B
3.C
4.A
5.B
6.B
7.C
8.2
9.(1,0)、(2,0);(0,2)
10.3
11.y= (x-2)2+1
12.;
13.直线x=-
14. ,
15.
16.解 :设解析式为:y=a(x+2)2﹣3,
将(﹣3,﹣1)代入得出:﹣1=a(﹣3+2)2﹣3,
解得: a=2.
故这个二次函数的解析式为:y=2(x+2)2﹣3
17.解:∵AB=4 ,CD=4 ,
∴A(-2 ,0),B(2 ,0),C(-2 ,4),D(2 ,4),
设函数的解析式为y=a(x-2 )(x+2 ),由题意,得
4=a(2 -2 )(2 +2 ),
解得a=- ,
则y=- (x-2 )(x+2 )=- x2+8.
当x=0时,
y=8,
则OM=8.
则水过警戒线后淹没到拱桥顶端M处的时间为:(8-4)÷0.5=8小时.
答:水过警戒线后淹没到拱桥顶端M处的时间为8小时.
18.解:∵△ABC为直角三角形,
∴∠ACB=90°,
∵∠ACO+∠BCO=90°,∠CBO+∠BCO=90°,
∴∠ACO=∠CBO,
∴△ACO∽△CBO,
∴ ,
∴OC2=OB·OA.
当y=0时, x2-mx+c=0,
∴x1·x2=2c,
∴OB·OA=-2c.
∵C(0,c),
∴OC=-c,
∴(-c)2=-2c,
∴c2+2c=0,
∴c1=0(舍去),c2=-2.
∴c的值是-2.
19.解:(1)∵设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元.
∴上涨后每件商品的利润为(10+x)元,每月能销售(210﹣10x)件商品;
由题意得:y=(210﹣10x)(50+x﹣40)
=﹣10x2+110x+2100
=﹣10(x﹣5.5)2+2402.5(0<x≤15且x为整数);
(2)∵a=﹣10<0,
∴当x=5.5时,y有最大值2402.5.
∵0<x≤15,且x为整数,
当x=5时,50+x=55,y=2400(元),当x=6时,50+x=56,y=2400(元)
∴当售价定为每件55或56元,每个月的利润最大,最大的月利润是2400元;
(3)当y=2200时,﹣10x2+110x+2100=2200,
解得:x1=1,x2=10.
∴当x=1时,50+x=51,当x=10时,50+x=60.
∴当售价定为每件51或60元,每个月的利润为2200元.
当售价不低于51或60元,每个月的利润为2200元.
当售价不低于51元且不高于60元且为整数时,每个月的利润不低于2200元(或当售价分别为51,52,53,54,55,56,57,58,59,60元时,每个月的利润不低于2200元).
20.解:(1)∵y=ax2+bx的顶点为(﹣),抛物线的顶点在直线y=kx上,k=1,抛物线水线最大高度达3m,
∴,,
解得,a=,b=2,
即k=1,且喷出的抛物线水线最大高度达3m,此时a、b的值分别是,2;
(2)∵k=1,喷出的水恰好达到岸边,出水口离岸边18m,抛物线的顶点在直线y=kx上,
∴此时抛物线的对称轴为x=9,y=x=9,
即此时喷出的抛物线水线最大高度是9米;
(3)∵y=ax2+bx的顶点为(﹣)在直线y=3x上,a=﹣,
∴,
解得,b=6,
∴抛物线y=,
当y=0时,0=,
解得,x1=21,x2=0,
∵21>18,
∴若k=3,a=﹣,则喷出的抛物线水线能达到岸边,
即若k=3,a=﹣,喷出的抛物线水线能达到岸边.
21.(1)解:设AB的长为x(m),则AD的长为:(m),
由题意可得,;
(2)解:由于强的长度不限,
∴,
解得.
22.解:(Ⅰ) ∵当 =0时, =4,∴C(0,4) ,OB=4OA, CBO=45°∴OC=OB=4, OA=1 A(-1,0) ,B(4,0)设 ,解得: =-1,(Ⅱ) 设P(m,-m2+3m+4),PCD是以CD为底边的等腰三角形时,过点P作PE⊥CD于E,CD=m CE=DE,OE=4- m,∴4- m=-m2+3m+4 m>0 m= ∴P( , )(Ⅲ)假设存在,过点P作PE⊥CD于点E,且交CB于H,过点P作PF⊥AB于F,P( , )这时CD=3.5 ,D(0,0.5)可求出直线PD的解析式: 可知直线PD 过点A(-1,0)若设∠APQ2=∠BCP= ∠CPE=∠EPA=∠PAB= , CBO= CHE= 45°,又 CHE= + ∴ + =45°= EPG = PGF ∴PF=FG= ,OG= - = ∴G( ,0), 可求出直线PG的解析式: 由 解得x1 = ,x2= (舍去)∴ Q2( , )作点G关于直线AP的对称点S,由于PD的解析式: ∴设GS的解析式: 过点G,得出 = , ,联立得: ,解得:求出点K( , )∵点K为SG的中点,求出S( , ) P( , ) ∴PS的解析式为: ∴ ,解得: (舍去) , ,∴Q1( , )
同课章节目录
