第三章 勾股定理期末章节拔高练习(含答案)
文档属性
| 名称 | 第三章 勾股定理期末章节拔高练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 631.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-29 09:07:04 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
苏科版数学八年级上册第三章勾股定理期末章节拔高练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去高六尺,折高者几何?意思是:一根竹子,原高一丈(一丈=十尺),一阵风将竹子折断,竹梢恰好抵地,抵地处离竹子底部6尺远,求折断处离地面的高度.设竹子折断处离地面x尺,根据题意,可列方程为( )
A. B.
C. D.
2.下列线段组成的三角形中,能构成直角三角形的是( )
A.,, B.13,14,15
C.a=,b=1,c= D.,,
3.如图,将三边长分别为3,4,5的沿最长边翻转成,则的长等于( )
A. B. C. D.
4.若为直角三角形的三边,则下列判断错误的是( )
A.能组成直角三角形 B.能组成直角三角形
C.能组成直角三角形 D.能组成直角三角形
5.已知在中,,则的长为( )
A. B. C.4 D.
6.由下列条件不能判定△ABC为直角三角形的是(其中a、b、c分别表示三角形的三边长)( )
A. B.
C. D.
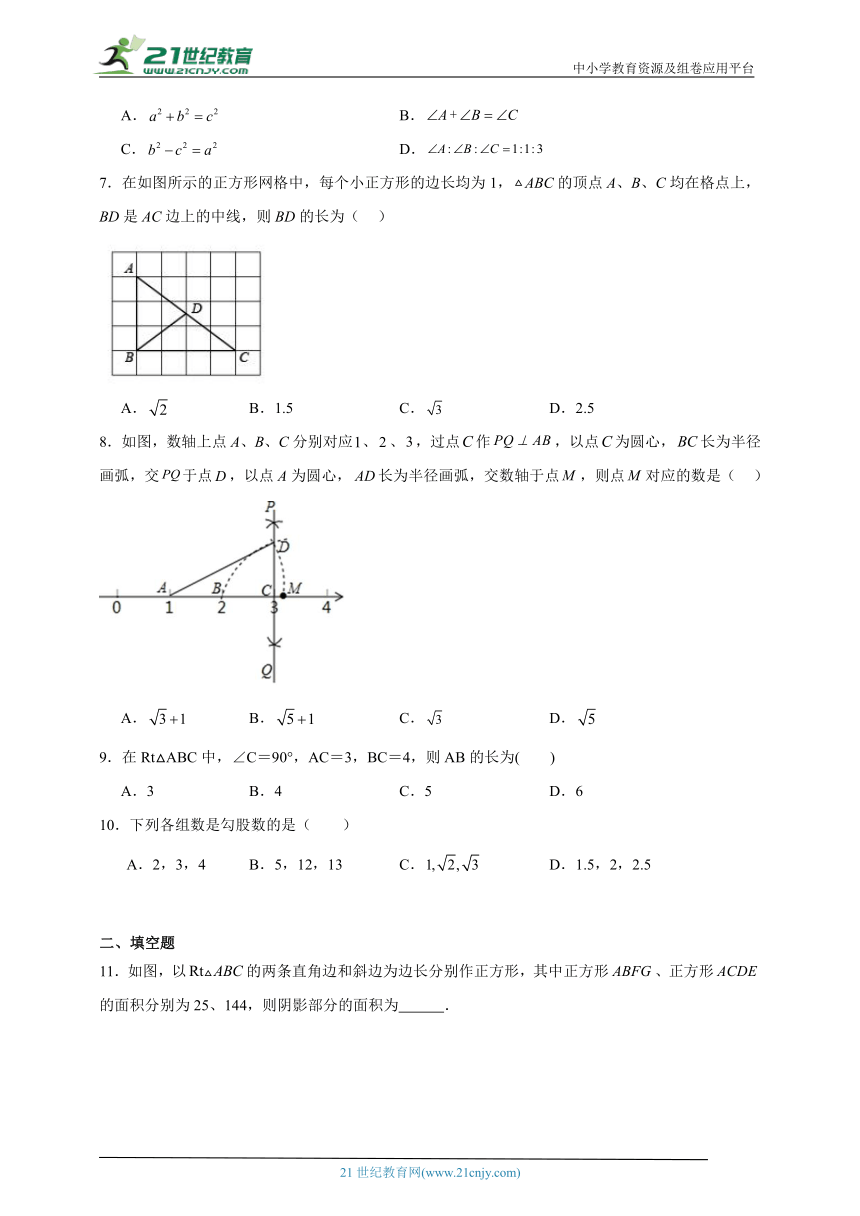
7.在如图所示的正方形网格中,每个小正方形的边长均为1,ABC的顶点A、B、C均在格点上,BD是AC边上的中线,则BD的长为( )
A. B.1.5 C. D.2.5
8.如图,数轴上点A、B、C分别对应、、,过点作,以点为圆心,长为半径画弧,交于点,以点A为圆心,长为半径画弧,交数轴于点,则点对应的数是( )
A. B. C. D.
9.在Rt△ABC中,∠C=90°,AC=3,BC=4,则AB的长为( )
A.3 B.4 C.5 D.6
10.下列各组数是勾股数的是( )
A.2,3,4 B.5,12,13 C. D.1.5,2,2.5
二、填空题
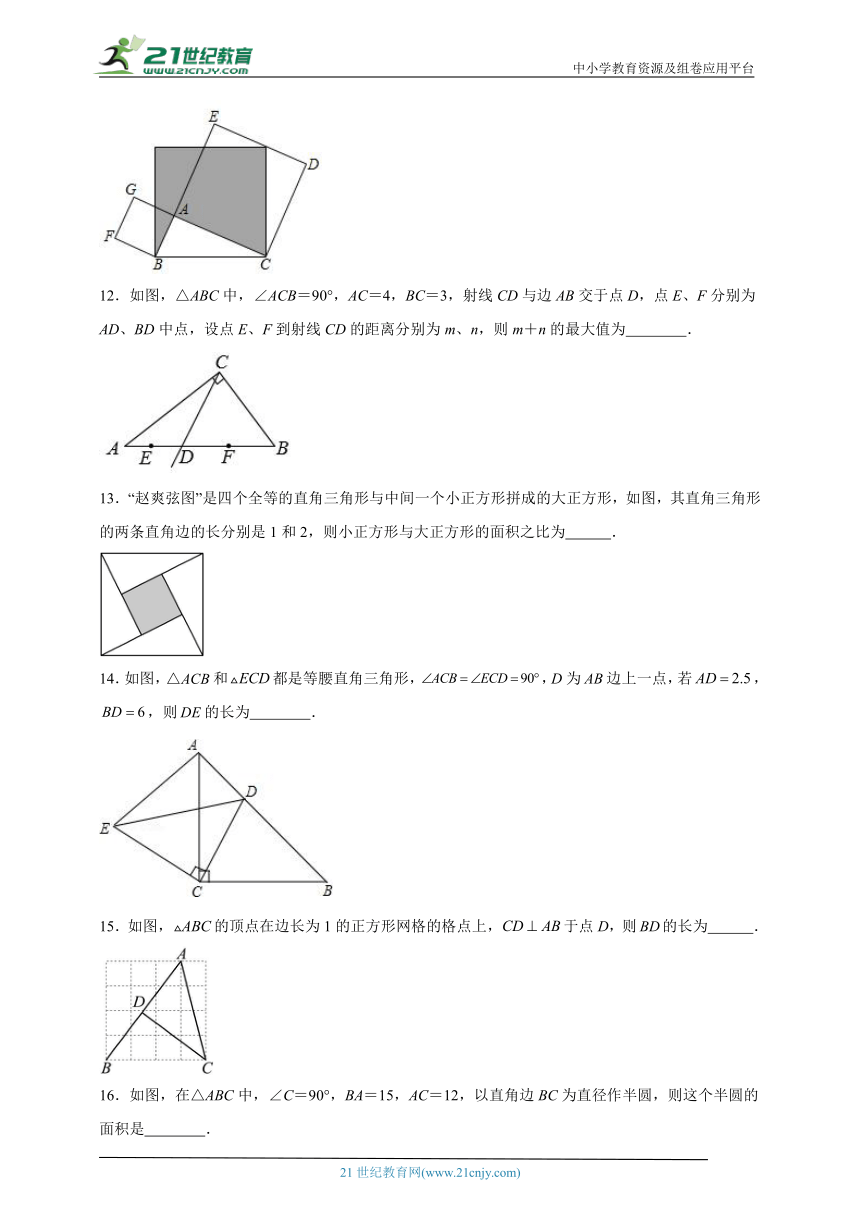
11.如图,以的两条直角边和斜边为边长分别作正方形,其中正方形、正方形的面积分别为25、144,则阴影部分的面积为 .
12.如图,△ABC中,∠ACB=90°,AC=4,BC=3,射线CD与边AB交于点D,点E、F分别为AD、BD中点,设点E、F到射线CD的距离分别为m、n,则m+n的最大值为 .
13.“赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形,如图,其直角三角形的两条直角边的长分别是1和2,则小正方形与大正方形的面积之比为 .
14.如图,和都是等腰直角三角形,,D为边上一点,若,,则的长为 .
15.如图,的顶点在边长为1的正方形网格的格点上,于点D,则的长为 .
16.如图,在△ABC中,∠C=90°,BA=15,AC=12,以直角边BC为直径作半圆,则这个半圆的面积是 .
17.一个长方体同一顶点的三条棱长分别是3、4、12,则这个长方体内能容下的最长的木棒为 .
18.如图,在中,,D在上,将沿直线翻折后,点A落在点E处,如果,那么的面积是 .
19.在一个长12米,宽为8米的长方形草地上,如图堆放着一根正三棱柱的木块,它的侧棱长平行且大于场地宽,木块的主视图是边长3米的等边三角形,一只蚂蚁从点A处到C处需要走的最短路程是 米.
20.点A、B、C在格点图中的位置如图所示,格点小正方形的边长为1,则点C到线段AB的距离是 .
三、解答题
21.某校八年级学生准备测量校园人工湖的深度,他们在保证安全的情况下把一根竹竿AB垂直插到离湖边3dm的水底(即),只见竹竿高出水面OC的距离,把竹竿的顶端拉向湖边(底端不变),竿顶A和湖沿的水面C处平齐(即),求湖水的深度OB和竹竿AB的长.
22.在中,,点D为的中点,点E、F分别在边、上,且满足.
(1)如图1,当时,若,,则= ;
(2)如图2,当时,求证:;
(3)如图3,当时将沿翻折,边与交于点G,若,,求的长.
23.如图,每个小正方形的边长都为l.点、、、均在网格交点上,求点到的距离.
参考答案:
1.D
2.C
3.D
4.D
5.C
6.D
7.D
8.B
9.C
10.B
11.139
12.2.5
13./1:5
14.6.5
15.
16.10.125π
17.13
18.1
19.17
20.
21.湖水的深度OB为4dm,竹竿AB的长为5dm .
22.(1)
(2)略
(3)28
23.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
苏科版数学八年级上册第三章勾股定理期末章节拔高练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去高六尺,折高者几何?意思是:一根竹子,原高一丈(一丈=十尺),一阵风将竹子折断,竹梢恰好抵地,抵地处离竹子底部6尺远,求折断处离地面的高度.设竹子折断处离地面x尺,根据题意,可列方程为( )
A. B.
C. D.
2.下列线段组成的三角形中,能构成直角三角形的是( )
A.,, B.13,14,15
C.a=,b=1,c= D.,,
3.如图,将三边长分别为3,4,5的沿最长边翻转成,则的长等于( )
A. B. C. D.
4.若为直角三角形的三边,则下列判断错误的是( )
A.能组成直角三角形 B.能组成直角三角形
C.能组成直角三角形 D.能组成直角三角形
5.已知在中,,则的长为( )
A. B. C.4 D.
6.由下列条件不能判定△ABC为直角三角形的是(其中a、b、c分别表示三角形的三边长)( )
A. B.
C. D.
7.在如图所示的正方形网格中,每个小正方形的边长均为1,ABC的顶点A、B、C均在格点上,BD是AC边上的中线,则BD的长为( )
A. B.1.5 C. D.2.5
8.如图,数轴上点A、B、C分别对应、、,过点作,以点为圆心,长为半径画弧,交于点,以点A为圆心,长为半径画弧,交数轴于点,则点对应的数是( )
A. B. C. D.
9.在Rt△ABC中,∠C=90°,AC=3,BC=4,则AB的长为( )
A.3 B.4 C.5 D.6
10.下列各组数是勾股数的是( )
A.2,3,4 B.5,12,13 C. D.1.5,2,2.5
二、填空题
11.如图,以的两条直角边和斜边为边长分别作正方形,其中正方形、正方形的面积分别为25、144,则阴影部分的面积为 .
12.如图,△ABC中,∠ACB=90°,AC=4,BC=3,射线CD与边AB交于点D,点E、F分别为AD、BD中点,设点E、F到射线CD的距离分别为m、n,则m+n的最大值为 .
13.“赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形,如图,其直角三角形的两条直角边的长分别是1和2,则小正方形与大正方形的面积之比为 .
14.如图,和都是等腰直角三角形,,D为边上一点,若,,则的长为 .
15.如图,的顶点在边长为1的正方形网格的格点上,于点D,则的长为 .
16.如图,在△ABC中,∠C=90°,BA=15,AC=12,以直角边BC为直径作半圆,则这个半圆的面积是 .
17.一个长方体同一顶点的三条棱长分别是3、4、12,则这个长方体内能容下的最长的木棒为 .
18.如图,在中,,D在上,将沿直线翻折后,点A落在点E处,如果,那么的面积是 .
19.在一个长12米,宽为8米的长方形草地上,如图堆放着一根正三棱柱的木块,它的侧棱长平行且大于场地宽,木块的主视图是边长3米的等边三角形,一只蚂蚁从点A处到C处需要走的最短路程是 米.
20.点A、B、C在格点图中的位置如图所示,格点小正方形的边长为1,则点C到线段AB的距离是 .
三、解答题
21.某校八年级学生准备测量校园人工湖的深度,他们在保证安全的情况下把一根竹竿AB垂直插到离湖边3dm的水底(即),只见竹竿高出水面OC的距离,把竹竿的顶端拉向湖边(底端不变),竿顶A和湖沿的水面C处平齐(即),求湖水的深度OB和竹竿AB的长.
22.在中,,点D为的中点,点E、F分别在边、上,且满足.
(1)如图1,当时,若,,则= ;
(2)如图2,当时,求证:;
(3)如图3,当时将沿翻折,边与交于点G,若,,求的长.
23.如图,每个小正方形的边长都为l.点、、、均在网格交点上,求点到的距离.
参考答案:
1.D
2.C
3.D
4.D
5.C
6.D
7.D
8.B
9.C
10.B
11.139
12.2.5
13./1:5
14.6.5
15.
16.10.125π
17.13
18.1
19.17
20.
21.湖水的深度OB为4dm,竹竿AB的长为5dm .
22.(1)
(2)略
(3)28
23.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
