第三章 勾股定理期末章节基础练习(含答案)
文档属性
| 名称 | 第三章 勾股定理期末章节基础练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 525.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-29 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
苏科版数学八年级上册第三章勾股定理期末章节基础练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.直角三角形有一条直角边长为13,另外两条边长都是自然数,则周长为( )
A.182 B.183 C.184 D.185
2.下列各组数中,满足勾股定理的是( )
A.32,42,52 B.,, C.,, D.9,40,41
3.图1是第七届国际数学教育大会()的会徽,图2由主体图案中相邻两个直角三角形组合而成,当,,时,的长为( )
A. B. C.4 D.
4.若以下列各组数值作为三角形的三边长,则不能围成直角三角形的是( )
A.4、6、8 B.3、4、5
C.5、12、13 D.1、3、
5.如图,所有阴影部分的四边形都是正方形,所有三角形都是直角三角形,已知正方形A、B、C的面积依次为2、4、3,则正方形D的面积为( )
A.7 B.8 C.9 D.10
6.下列线段中,能组成直角三角形的是( )
A.1,2,3 B.2,3,4 C.2,4,5 D.3,4,5
7.下列各组数是勾股数的是( )
A.6,7,8 B.1,,2
C.5,4,3 D.0.3,0.4,0.5
8.下列各组数据中不能作为直角三角形三边长的是( )
A.3、4、6 B.7、24、25
C.6、8、10 D.9、12、15
9.下列几组数,能作为直角三角形的三边长的是( )
A.6,8,9 B.6,8,10 C.6,8,11 D.6,8,12
10.如图,在中,,按以下步骤作图:①以C为圆心,CB的长为半径作弧,交AB于点D;②分别以点D,B为圆心,大于的长为半径作弧,两弧交于点E;③作射线CE,交边AB于点F.若,则线段AD的长为( )
A. B.1 C. D.
二、填空题
11.一个三角形三边长为15、20、25,则三角形的面积为 .
12.如图,在的两边上有两点和在运动,且点从离点有厘米远的地方出发,以厘米每秒运动,点从点出发以厘米每秒运动,则为等腰三角形时,两点的运动时间为 秒.
13.如图,某公园处有一块长方形草坪,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”AB.已知,,他们踩伤草坪,仅仅少走了 .
14.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为,较短直角边长为,若,小正方形的面积为,则大正方形的面积为 .
15.《算法统宗》是中国古代数学名著,作者是我国明代数学家程大位.在《算法统宗》中有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?”小明同学根据原文题意,画出示意图如图所示.已知:秋千静止时,踏板离地1尺,将它推送2步(水平距离)时,秋千的踏板就和身高为5尺的曾记一样高,秋千的绳索始终拉得很直.若小明同学根据题意计算出秋千的绳索长为14.5尺,则文中“两步”是 尺.
16.已知一个三角形的三边分别是6cm、8cm、10cm,则这个三角形的面积是 .
17.如图,已知在5×5的正方形网格中,点A、B、C在小正方形的顶点上,如果小正方形的边长都为1,那么点C到线段AB所在直线的距离是 .
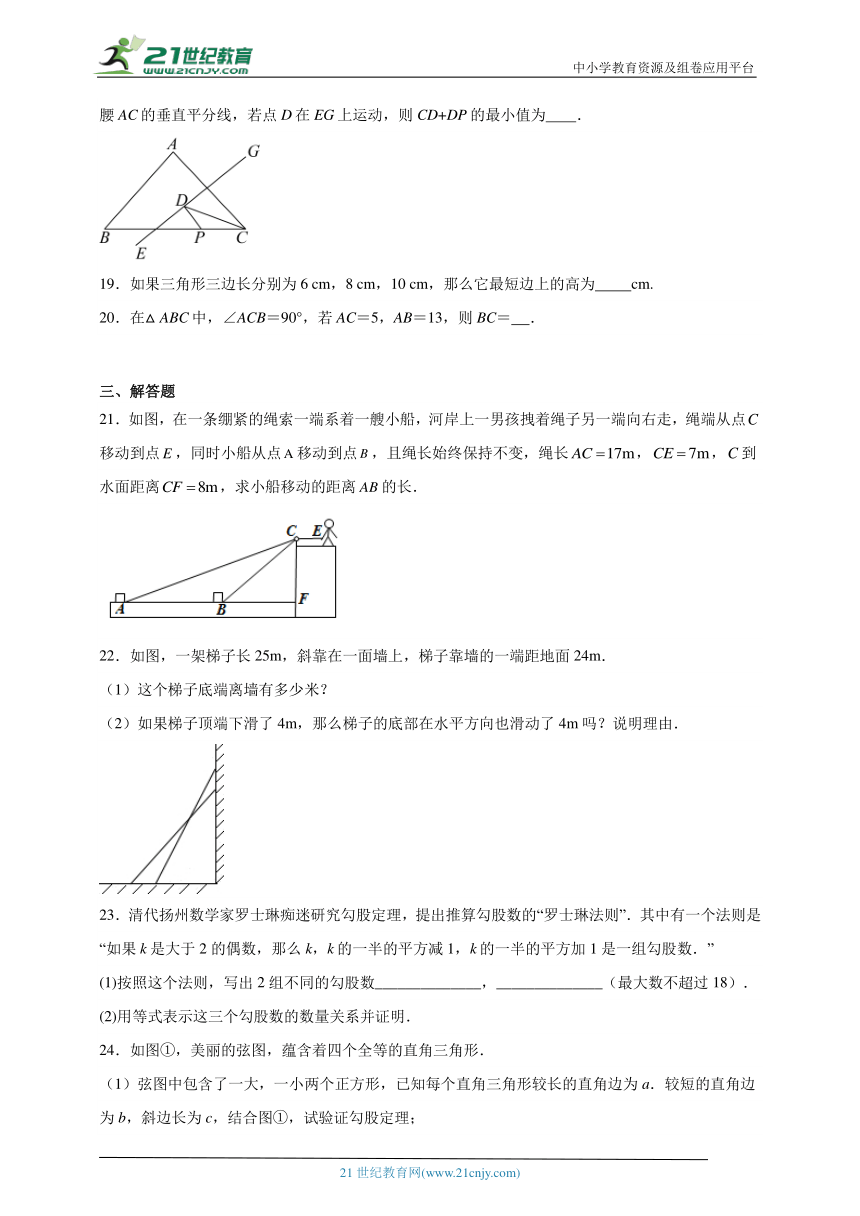
18.如图,等腰三角形ABC的面积为24,底边BC为12,点P在BC边上,且,EG是腰AC的垂直平分线,若点D在EG上运动,则CD+DP的最小值为 .
19.如果三角形三边长分别为6 cm,8 cm,10 cm,那么它最短边上的高为 cm.
20.在△ABC中,∠ACB=90°,若AC=5,AB=13,则BC= .
三、解答题
21.如图,在一条绷紧的绳索一端系着一艘小船,河岸上一男孩拽着绳子另一端向右走,绳端从点移动到点,同时小船从点移动到点,且绳长始终保持不变,绳长,,到水面距离,求小船移动的距离的长.
22.如图,一架梯子长25m,斜靠在一面墙上,梯子靠墙的一端距地面24m.
(1)这个梯子底端离墙有多少米?
(2)如果梯子顶端下滑了4m,那么梯子的底部在水平方向也滑动了4m吗?说明理由.
23.清代扬州数学家罗士琳痴迷研究勾股定理,提出推算勾股数的“罗士琳法则”.其中有一个法则是“如果k是大于2的偶数,那么k,k的一半的平方减1,k的一半的平方加1是一组勾股数.”
(1)按照这个法则,写出2组不同的勾股数______________,______________(最大数不超过18).
(2)用等式表示这三个勾股数的数量关系并证明.
24.如图①,美丽的弦图,蕴含着四个全等的直角三角形.
(1)弦图中包含了一大,一小两个正方形,已知每个直角三角形较长的直角边为a.较短的直角边为b,斜边长为c,结合图①,试验证勾股定理;
(2)如图②,将这四个直角三角形紧密地拼接,形成飞镖状,已知外围轮廓(粗线)的周长为24,OC=3,求该飞镖状图案的面积;
(3)如图③,将八个全等的直角三角形紧密地拼接,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1、S2、S3,若S1+S2+S3=16,则S2= .
25.如图,在下列10×10的网格中,横、纵坐标均为整点的数叫做格点,例如A(2,1)、B(5,4)、C(1,8)都是格点.
(1)直接写出△ABC的形状.
(2)要求在下图中仅用无刻度的直尺作图:将△ABC绕点A顺时针旋转角度α得到△AB1C1,α=∠BAC,其中B,C的对应点分别为B1,C1,操作如下:
第一步:找一个格点D,连接AD,使∠DAB=∠CAB.
第二步:找两个格点C1,E,连接C1E交AD于B1.
第三步:连接AC1,则△AB1C1即为所作出的图形.
请你按步骤完成作图,并直接写出D、C1、E三点的坐标.
参考答案:
1.A
2.D
3.B
4.A
5.C
6.D
7.C
8.A
9.B
10.B
11.150
12.1或或
13.20
14.
15.10
16.24cm2.
17.
18.5
19.8
20.12
21.
22.(1)7m;(2)不是滑动了4m而是滑动了8m
23.(1)3,4,5;6,8,10
(2)(k是大于2的偶数)
24.(1)略;(2)该飞镖状图案的面积是24;(3).
25.(1)△ABC是直角三角形;(2)D(9,0),C1(7,6),E(6,﹣1).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
苏科版数学八年级上册第三章勾股定理期末章节基础练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.直角三角形有一条直角边长为13,另外两条边长都是自然数,则周长为( )
A.182 B.183 C.184 D.185
2.下列各组数中,满足勾股定理的是( )
A.32,42,52 B.,, C.,, D.9,40,41
3.图1是第七届国际数学教育大会()的会徽,图2由主体图案中相邻两个直角三角形组合而成,当,,时,的长为( )
A. B. C.4 D.
4.若以下列各组数值作为三角形的三边长,则不能围成直角三角形的是( )
A.4、6、8 B.3、4、5
C.5、12、13 D.1、3、
5.如图,所有阴影部分的四边形都是正方形,所有三角形都是直角三角形,已知正方形A、B、C的面积依次为2、4、3,则正方形D的面积为( )
A.7 B.8 C.9 D.10
6.下列线段中,能组成直角三角形的是( )
A.1,2,3 B.2,3,4 C.2,4,5 D.3,4,5
7.下列各组数是勾股数的是( )
A.6,7,8 B.1,,2
C.5,4,3 D.0.3,0.4,0.5
8.下列各组数据中不能作为直角三角形三边长的是( )
A.3、4、6 B.7、24、25
C.6、8、10 D.9、12、15
9.下列几组数,能作为直角三角形的三边长的是( )
A.6,8,9 B.6,8,10 C.6,8,11 D.6,8,12
10.如图,在中,,按以下步骤作图:①以C为圆心,CB的长为半径作弧,交AB于点D;②分别以点D,B为圆心,大于的长为半径作弧,两弧交于点E;③作射线CE,交边AB于点F.若,则线段AD的长为( )
A. B.1 C. D.
二、填空题
11.一个三角形三边长为15、20、25,则三角形的面积为 .
12.如图,在的两边上有两点和在运动,且点从离点有厘米远的地方出发,以厘米每秒运动,点从点出发以厘米每秒运动,则为等腰三角形时,两点的运动时间为 秒.
13.如图,某公园处有一块长方形草坪,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”AB.已知,,他们踩伤草坪,仅仅少走了 .
14.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为,较短直角边长为,若,小正方形的面积为,则大正方形的面积为 .
15.《算法统宗》是中国古代数学名著,作者是我国明代数学家程大位.在《算法统宗》中有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?”小明同学根据原文题意,画出示意图如图所示.已知:秋千静止时,踏板离地1尺,将它推送2步(水平距离)时,秋千的踏板就和身高为5尺的曾记一样高,秋千的绳索始终拉得很直.若小明同学根据题意计算出秋千的绳索长为14.5尺,则文中“两步”是 尺.
16.已知一个三角形的三边分别是6cm、8cm、10cm,则这个三角形的面积是 .
17.如图,已知在5×5的正方形网格中,点A、B、C在小正方形的顶点上,如果小正方形的边长都为1,那么点C到线段AB所在直线的距离是 .
18.如图,等腰三角形ABC的面积为24,底边BC为12,点P在BC边上,且,EG是腰AC的垂直平分线,若点D在EG上运动,则CD+DP的最小值为 .
19.如果三角形三边长分别为6 cm,8 cm,10 cm,那么它最短边上的高为 cm.
20.在△ABC中,∠ACB=90°,若AC=5,AB=13,则BC= .
三、解答题
21.如图,在一条绷紧的绳索一端系着一艘小船,河岸上一男孩拽着绳子另一端向右走,绳端从点移动到点,同时小船从点移动到点,且绳长始终保持不变,绳长,,到水面距离,求小船移动的距离的长.
22.如图,一架梯子长25m,斜靠在一面墙上,梯子靠墙的一端距地面24m.
(1)这个梯子底端离墙有多少米?
(2)如果梯子顶端下滑了4m,那么梯子的底部在水平方向也滑动了4m吗?说明理由.
23.清代扬州数学家罗士琳痴迷研究勾股定理,提出推算勾股数的“罗士琳法则”.其中有一个法则是“如果k是大于2的偶数,那么k,k的一半的平方减1,k的一半的平方加1是一组勾股数.”
(1)按照这个法则,写出2组不同的勾股数______________,______________(最大数不超过18).
(2)用等式表示这三个勾股数的数量关系并证明.
24.如图①,美丽的弦图,蕴含着四个全等的直角三角形.
(1)弦图中包含了一大,一小两个正方形,已知每个直角三角形较长的直角边为a.较短的直角边为b,斜边长为c,结合图①,试验证勾股定理;
(2)如图②,将这四个直角三角形紧密地拼接,形成飞镖状,已知外围轮廓(粗线)的周长为24,OC=3,求该飞镖状图案的面积;
(3)如图③,将八个全等的直角三角形紧密地拼接,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1、S2、S3,若S1+S2+S3=16,则S2= .
25.如图,在下列10×10的网格中,横、纵坐标均为整点的数叫做格点,例如A(2,1)、B(5,4)、C(1,8)都是格点.
(1)直接写出△ABC的形状.
(2)要求在下图中仅用无刻度的直尺作图:将△ABC绕点A顺时针旋转角度α得到△AB1C1,α=∠BAC,其中B,C的对应点分别为B1,C1,操作如下:
第一步:找一个格点D,连接AD,使∠DAB=∠CAB.
第二步:找两个格点C1,E,连接C1E交AD于B1.
第三步:连接AC1,则△AB1C1即为所作出的图形.
请你按步骤完成作图,并直接写出D、C1、E三点的坐标.
参考答案:
1.A
2.D
3.B
4.A
5.C
6.D
7.C
8.A
9.B
10.B
11.150
12.1或或
13.20
14.
15.10
16.24cm2.
17.
18.5
19.8
20.12
21.
22.(1)7m;(2)不是滑动了4m而是滑动了8m
23.(1)3,4,5;6,8,10
(2)(k是大于2的偶数)
24.(1)略;(2)该飞镖状图案的面积是24;(3).
25.(1)△ABC是直角三角形;(2)D(9,0),C1(7,6),E(6,﹣1).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
