人教版九年级数学上册第22章《二次函数》期末复习题 (7)(含答案)
文档属性
| 名称 | 人教版九年级数学上册第22章《二次函数》期末复习题 (7)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 126.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-28 16:40:44 | ||
图片预览



文档简介
第22章《二次函数》期末复习题
一、选择题
1.下列各式中,y是x的二次函数的是( )
A.y=x2﹣(x﹣1)x B.y+ax2=﹣3
C.x2=2y+3 D.y=x2+x﹣2
2.抛物线 与x轴的交点个数为( )
A.0 B.1 C.2 D.3
3.如果二次函数 的图像如图所示,那么一次函数 的图像经过( )
A.第一、二、三象限 B.第一、三、四象限
C.第一、二、四象限 D.第二、三、四象限
4.点 均在抛物线 上,下列说法正确的是( )
A.若 ,则 B.若 ,则
C.若 ,则 D.若 ,则
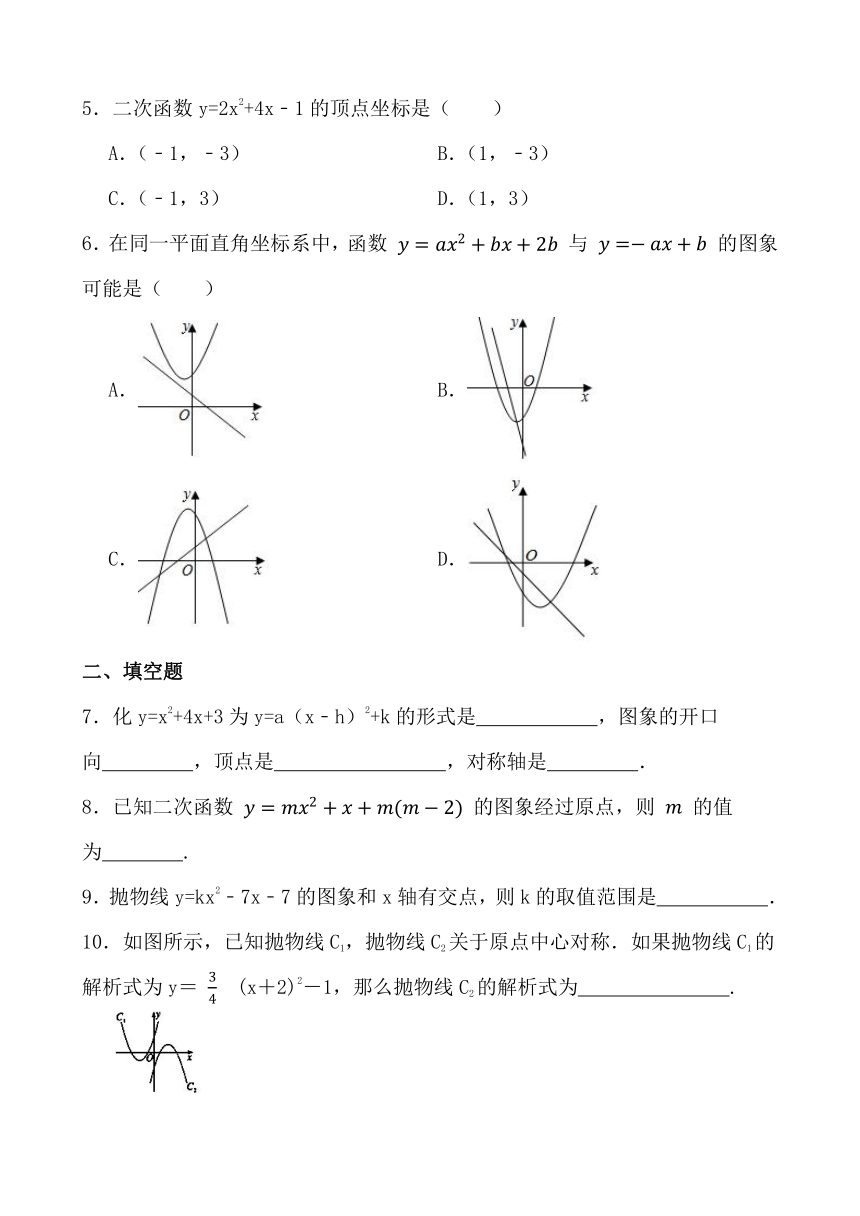
5.二次函数y=2x2+4x﹣1的顶点坐标是( )
A.(﹣1,﹣3) B.(1,﹣3)
C.(﹣1,3) D.(1,3)
6.在同一平面直角坐标系中,函数 与 的图象可能是( )
A. B.
C. D.
二、填空题
7.化y=x2+4x+3为y=a(x﹣h)2+k的形式是 ,图象的开口向 ,顶点是 ,对称轴是 .
8.已知二次函数 的图象经过原点,则 的值为 .
9.抛物线y=kx2﹣7x﹣7的图象和x轴有交点,则k的取值范围是 .
10.如图所示,已知抛物线C1,抛物线C2关于原点中心对称.如果抛物线C1的解析式为y= (x+2)2-1,那么抛物线C2的解析式为 .
11.已知二次函数y=2x2﹣8x+6的图象交x轴于A,B两点.若其图象上有且只有P1,P2,P3三点满足S△ABP1=S△ABP2=S△ABP3=m,则m的值为 .
12.抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,其与x轴的一个交点坐标为(﹣3,0),对称轴为x=﹣1,则当y<0时,x的取值范围是 .
13.二次函数 的图象如图所示,若 , .则 、 的大小关系为 .(填“ ”、“ ”或“ ”)
三、解答题
14.已知二次函数 的顶点坐标为 ,并经过 点,求二次函数的解析式,并在所给的坐标平面内画出这条抛物线.(不要求列表)
15.扎西的爷爷用一段长30m的篱笆围成一个一边靠墙的矩形菜园,墙长为18m,这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
16.一玩具厂去年生产某种玩具,成本为10元/件,出厂价为12元/件,年销售量为2万件.今年计划通过适当增加成本来提高产品档次,以拓展市场.若今年这种玩具每件的成本比去年成本增加0.7x倍,今年这种玩具每件的出厂价比去年出厂价相应提高0.5x倍,则预计今年年销售量将比去年年销售量增加x倍(本题中0<x≤1).
(1)用含x的代数式表示,今年生产的这种玩具每件的成本为多少元,今年生产的这种玩具每件的出厂价为多少元.
(2)求今年这种玩具的每件利润y元与x之间的函数关系式.
(3)设今年这种玩具的年销售利润为w万元,求当x为何值时,今年的年销售利润最大?最大年销售利润是多少万元?注:年销售利润=(每件玩具的出厂价﹣每件玩具的成本)×年销售量.
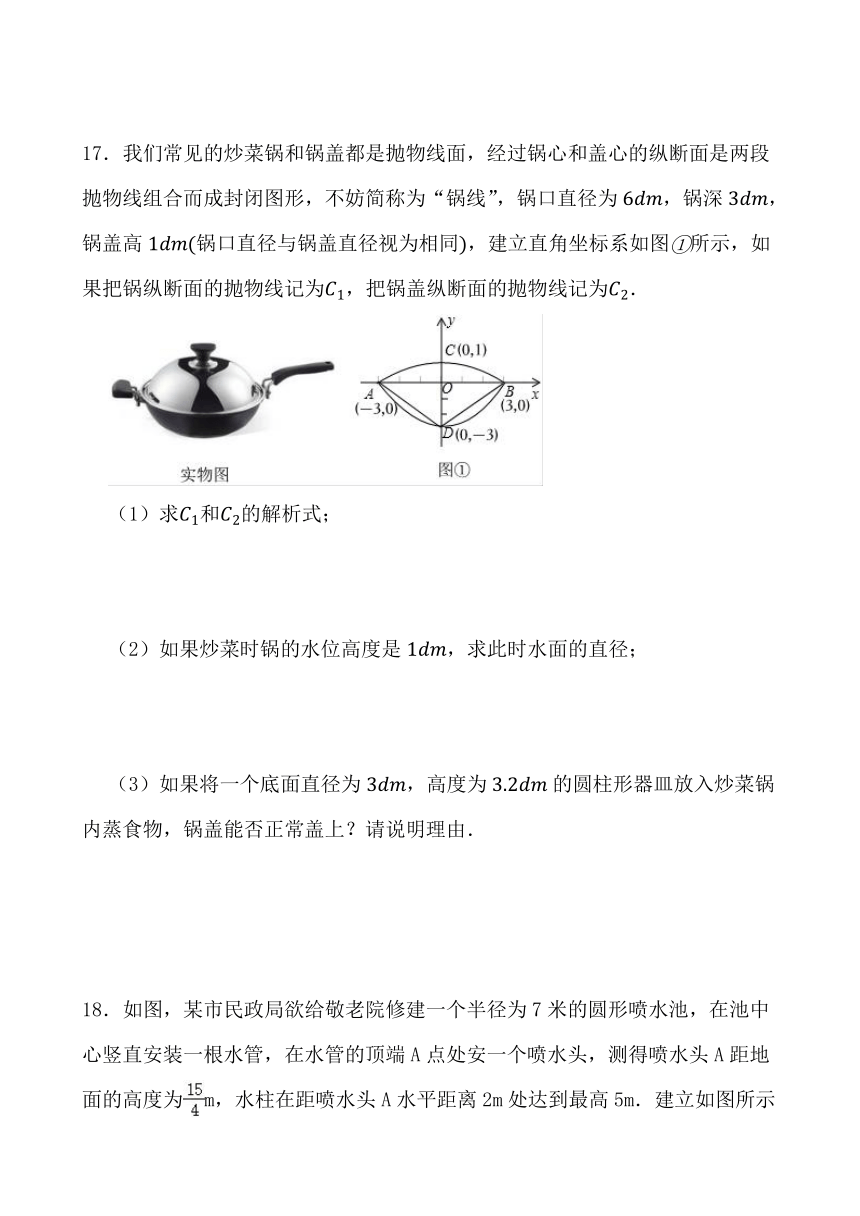
17.我们常见的炒菜锅和锅盖都是抛物线面,经过锅心和盖心的纵断面是两段抛物线组合而成封闭图形,不妨简称为“锅线”,锅口直径为,锅深,锅盖高锅口直径与锅盖直径视为相同,建立直角坐标系如图所示,如果把锅纵断面的抛物线记为,把锅盖纵断面的抛物线记为.
(1)求和的解析式;
(2)如果炒菜时锅的水位高度是,求此时水面的直径;
(3)如果将一个底面直径为,高度为的圆柱形器皿放入炒菜锅内蒸食物,锅盖能否正常盖上?请说明理由.
18.如图,某市民政局欲给敬老院修建一个半径为7米的圆形喷水池,在池中心竖直安装一根水管,在水管的顶端A点处安一个喷水头,测得喷水头A距地面的高度为m,水柱在距喷水头A水平距离2m处达到最高5m.建立如图所示的平面直角坐标系,并设抛物线的表达式为y=a(x-h)2+k,其中x(m)是水柱距喷水头的水平距离,y(m)是水柱距地面的高度.
(1)求抛物线的表达式;
(2)请你通过计算说明喷出的水柱是否会落到圆形喷水池的外面.
19.如图,一次函数的图象与二次函数的图象交于点和,与轴交于点.
(1)求的值;
(2)求的面积.
20.某菜农搭建了一个横截面为抛物线的大棚,尺寸如图:
(1)如图建立平面直角坐标系,使抛物线对称轴为y轴,求该抛物线的解析式;
(2)若需要开一个截面为矩形的门(如图所示),已知门的高度为1.60米,那么门的宽度最大是多少米(不考虑材料厚度) (结果保留根号)
答案解析部分
1.C
2.C
3.B
4.D
5.A
6.D
7.y=(x+2)2﹣1;上;(﹣2,﹣1);x=﹣2
8.2
9.k≥- 且k≠0
10.y= (x-2)2+1
11.2
12.﹣3<x<1
13.<
14.解:依题意设二次函数的解析式为 ,
将 , 代入,得 ,
解得 ,
∴二次函数的解析式为 ;
如图所示.
15.解:设矩形的宽为xm,面积为Sm2,根据题意得:
S=x(30-2x)
= -2x2+30x
= -2(x-7.5)2+112.5,
所以当x=7.5时,S最大,最大值为112.5.
30-2x=30-15=15
16.解:(1)10+7x;12+6x;
(2)y=(12+6x)﹣(10+7x),
∴y=2﹣x (0<x≤1);
(3)∵w=2(1+x) y
=2(1+x)(2﹣x)
=﹣2x2+2x+4,
∴w=﹣2(x﹣0.5)2+4.5
∵﹣2<0,0<x≤1,
∴w有最大值,
∴当x=0.5时,w最大=4.5(万元).
答:当x为0.5时,今年的年销售利润最大,最大年销售利润是4.5万元.
17.(1)解:由于抛物线、都过点、,可设它们的解析式为:;
抛物线还经过,
则有:,解得:,
即:抛物线:;
抛物线还经过,
则有:,解得:,
即:抛物线:.
(2)解:当炒菜锅里的水位高度为时,,即,
解得:,
此时水面的直径为.
(3)解:锅盖不能正常盖上,理由如下:
当时,抛物线:,抛物线:,
而,
锅盖不能正常盖上.
18.(1)解:由题意可知,抛物线的顶点坐标为(2,5),
则h=2,k=5,
∴抛物线的表达式为 y=a(x-2)2+5,
将A(0, )代入上式得,
,
解得,,
∴抛物线的表达式为 .
(2)解:当y=0时,,
解得,x1=6,x2=-2 (舍去),
∵6<7,
∴喷出的水柱不会落到圆形喷水池的外面.
19.(1)解:把点的坐标代入中,得,二次函数的解析式为,
把点的代入中,得点坐标为,
把和的坐标代入中,
得解得,;
(2)解:令中,则点坐标为,
,
.
20.(1)由图可设抛物线的解析式为:,
由图知抛物线与轴正半轴的交点为(2,0),则,
∴,
∴抛物线的解析式为:
(2)当y=1.60时,得:x=,
所以门的宽度最大为-(-)=米。
一、选择题
1.下列各式中,y是x的二次函数的是( )
A.y=x2﹣(x﹣1)x B.y+ax2=﹣3
C.x2=2y+3 D.y=x2+x﹣2
2.抛物线 与x轴的交点个数为( )
A.0 B.1 C.2 D.3
3.如果二次函数 的图像如图所示,那么一次函数 的图像经过( )
A.第一、二、三象限 B.第一、三、四象限
C.第一、二、四象限 D.第二、三、四象限
4.点 均在抛物线 上,下列说法正确的是( )
A.若 ,则 B.若 ,则
C.若 ,则 D.若 ,则
5.二次函数y=2x2+4x﹣1的顶点坐标是( )
A.(﹣1,﹣3) B.(1,﹣3)
C.(﹣1,3) D.(1,3)
6.在同一平面直角坐标系中,函数 与 的图象可能是( )
A. B.
C. D.
二、填空题
7.化y=x2+4x+3为y=a(x﹣h)2+k的形式是 ,图象的开口向 ,顶点是 ,对称轴是 .
8.已知二次函数 的图象经过原点,则 的值为 .
9.抛物线y=kx2﹣7x﹣7的图象和x轴有交点,则k的取值范围是 .
10.如图所示,已知抛物线C1,抛物线C2关于原点中心对称.如果抛物线C1的解析式为y= (x+2)2-1,那么抛物线C2的解析式为 .
11.已知二次函数y=2x2﹣8x+6的图象交x轴于A,B两点.若其图象上有且只有P1,P2,P3三点满足S△ABP1=S△ABP2=S△ABP3=m,则m的值为 .
12.抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,其与x轴的一个交点坐标为(﹣3,0),对称轴为x=﹣1,则当y<0时,x的取值范围是 .
13.二次函数 的图象如图所示,若 , .则 、 的大小关系为 .(填“ ”、“ ”或“ ”)
三、解答题
14.已知二次函数 的顶点坐标为 ,并经过 点,求二次函数的解析式,并在所给的坐标平面内画出这条抛物线.(不要求列表)
15.扎西的爷爷用一段长30m的篱笆围成一个一边靠墙的矩形菜园,墙长为18m,这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
16.一玩具厂去年生产某种玩具,成本为10元/件,出厂价为12元/件,年销售量为2万件.今年计划通过适当增加成本来提高产品档次,以拓展市场.若今年这种玩具每件的成本比去年成本增加0.7x倍,今年这种玩具每件的出厂价比去年出厂价相应提高0.5x倍,则预计今年年销售量将比去年年销售量增加x倍(本题中0<x≤1).
(1)用含x的代数式表示,今年生产的这种玩具每件的成本为多少元,今年生产的这种玩具每件的出厂价为多少元.
(2)求今年这种玩具的每件利润y元与x之间的函数关系式.
(3)设今年这种玩具的年销售利润为w万元,求当x为何值时,今年的年销售利润最大?最大年销售利润是多少万元?注:年销售利润=(每件玩具的出厂价﹣每件玩具的成本)×年销售量.
17.我们常见的炒菜锅和锅盖都是抛物线面,经过锅心和盖心的纵断面是两段抛物线组合而成封闭图形,不妨简称为“锅线”,锅口直径为,锅深,锅盖高锅口直径与锅盖直径视为相同,建立直角坐标系如图所示,如果把锅纵断面的抛物线记为,把锅盖纵断面的抛物线记为.
(1)求和的解析式;
(2)如果炒菜时锅的水位高度是,求此时水面的直径;
(3)如果将一个底面直径为,高度为的圆柱形器皿放入炒菜锅内蒸食物,锅盖能否正常盖上?请说明理由.
18.如图,某市民政局欲给敬老院修建一个半径为7米的圆形喷水池,在池中心竖直安装一根水管,在水管的顶端A点处安一个喷水头,测得喷水头A距地面的高度为m,水柱在距喷水头A水平距离2m处达到最高5m.建立如图所示的平面直角坐标系,并设抛物线的表达式为y=a(x-h)2+k,其中x(m)是水柱距喷水头的水平距离,y(m)是水柱距地面的高度.
(1)求抛物线的表达式;
(2)请你通过计算说明喷出的水柱是否会落到圆形喷水池的外面.
19.如图,一次函数的图象与二次函数的图象交于点和,与轴交于点.
(1)求的值;
(2)求的面积.
20.某菜农搭建了一个横截面为抛物线的大棚,尺寸如图:
(1)如图建立平面直角坐标系,使抛物线对称轴为y轴,求该抛物线的解析式;
(2)若需要开一个截面为矩形的门(如图所示),已知门的高度为1.60米,那么门的宽度最大是多少米(不考虑材料厚度) (结果保留根号)
答案解析部分
1.C
2.C
3.B
4.D
5.A
6.D
7.y=(x+2)2﹣1;上;(﹣2,﹣1);x=﹣2
8.2
9.k≥- 且k≠0
10.y= (x-2)2+1
11.2
12.﹣3<x<1
13.<
14.解:依题意设二次函数的解析式为 ,
将 , 代入,得 ,
解得 ,
∴二次函数的解析式为 ;
如图所示.
15.解:设矩形的宽为xm,面积为Sm2,根据题意得:
S=x(30-2x)
= -2x2+30x
= -2(x-7.5)2+112.5,
所以当x=7.5时,S最大,最大值为112.5.
30-2x=30-15=15
16.解:(1)10+7x;12+6x;
(2)y=(12+6x)﹣(10+7x),
∴y=2﹣x (0<x≤1);
(3)∵w=2(1+x) y
=2(1+x)(2﹣x)
=﹣2x2+2x+4,
∴w=﹣2(x﹣0.5)2+4.5
∵﹣2<0,0<x≤1,
∴w有最大值,
∴当x=0.5时,w最大=4.5(万元).
答:当x为0.5时,今年的年销售利润最大,最大年销售利润是4.5万元.
17.(1)解:由于抛物线、都过点、,可设它们的解析式为:;
抛物线还经过,
则有:,解得:,
即:抛物线:;
抛物线还经过,
则有:,解得:,
即:抛物线:.
(2)解:当炒菜锅里的水位高度为时,,即,
解得:,
此时水面的直径为.
(3)解:锅盖不能正常盖上,理由如下:
当时,抛物线:,抛物线:,
而,
锅盖不能正常盖上.
18.(1)解:由题意可知,抛物线的顶点坐标为(2,5),
则h=2,k=5,
∴抛物线的表达式为 y=a(x-2)2+5,
将A(0, )代入上式得,
,
解得,,
∴抛物线的表达式为 .
(2)解:当y=0时,,
解得,x1=6,x2=-2 (舍去),
∵6<7,
∴喷出的水柱不会落到圆形喷水池的外面.
19.(1)解:把点的坐标代入中,得,二次函数的解析式为,
把点的代入中,得点坐标为,
把和的坐标代入中,
得解得,;
(2)解:令中,则点坐标为,
,
.
20.(1)由图可设抛物线的解析式为:,
由图知抛物线与轴正半轴的交点为(2,0),则,
∴,
∴抛物线的解析式为:
(2)当y=1.60时,得:x=,
所以门的宽度最大为-(-)=米。
同课章节目录
