2.7有理数的减法跟踪训练(含详细解析)
文档属性
| 名称 | 2.7有理数的减法跟踪训练(含详细解析) |  | |
| 格式 | zip | ||
| 文件大小 | 33.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-24 07:45:46 | ||
图片预览


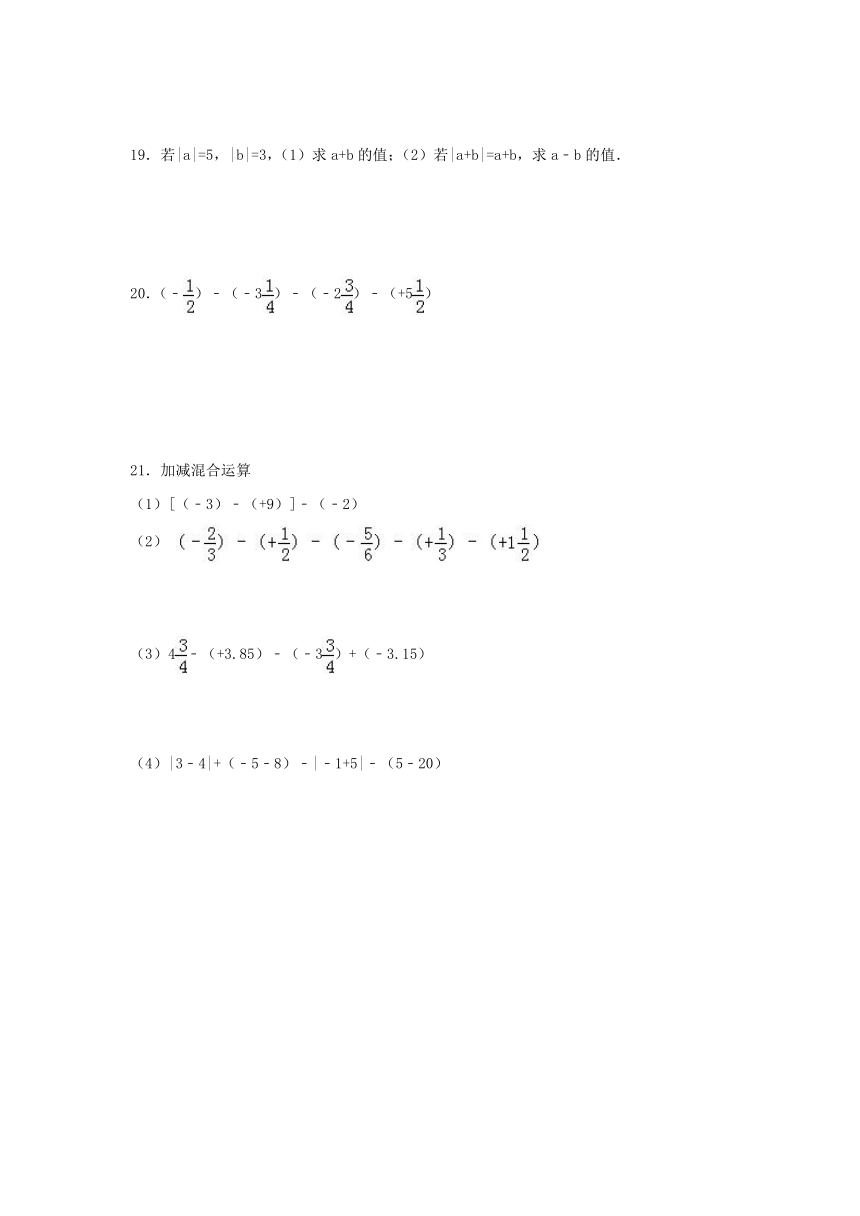


文档简介
第二章2.7有理数的减法
农安县合隆中学 徐亚惠
一.选择题(共8小题)
1.如果崇左市市区某中午的气温是37℃,到下午下降了3℃,那么下午的气温是( )
A.40℃ B.38℃ C.36℃ D.34℃
2.哈市某天的最高气温为28℃,最低气温为21℃,则这一天的最高气温与最低气温的差为( )
A.5℃ B.6℃ C.7℃ D.8℃
3.下列各数中,比﹣2小1的是( )
A.﹣1 B.0 C.﹣3 D.3
4.计算(﹣3)﹣(﹣9)的结果等于( )
A.12 B.﹣12 C.6 D.﹣6
5.﹣2013﹣2014的值为( )
A.1 B.4027 C.﹣4027 D.﹣1
6.石家庄某市的最高气温是1℃,最低气温是﹣3℃,该天的温差是( )
A.2℃ B.3℃ C.4℃ D.5℃
7.气温由﹣1℃下降5℃后是( )
A.﹣5℃ B.4℃ C.﹣4℃ D.﹣6℃
8.计算,正确的结果为( )
A. B. C. D.
二.填空题(共6小题)
9.计算:2000﹣2015= _________ .
10.若x=4,则|x﹣5|= _________ .
11.定义运算,则(﹣2) (﹣3)= _________ .
12.月球表面温度,中午是101℃,半夜是﹣150℃,则半夜比中午低 _________ ℃.
13.计算:﹣|﹣2|= _________ .
14.一只温度计刻度均匀但示数不准,将它放 ( http: / / www.21cnjy.com )入沸水中,示数为95摄氏度,放在冰水混合物中示数为﹣5摄氏度,当它的示数为32摄氏度时,实际温度是 _________ ℃.
三.解答题(共7小题)
15.计算:(﹣)﹣(﹣1)﹣(﹣1)﹣(+1.75).
16.用有理数的加法律计算:[(﹣72)﹣(﹣35)]﹣[(﹣23)﹣8].
17.若|a|=3,|b|=5,求a﹣b的值.
18.计算:1﹣1﹣2﹣3﹣4﹣5﹣6﹣7﹣8﹣9﹣10﹣…﹣1009.
19.若|a|=5,|b|=3,(1)求a+b的值;(2)若|a+b|=a+b,求a﹣b的值.
20.(﹣)﹣(﹣3)﹣(﹣2)﹣(+5)
21.加减混合运算
(1)[(﹣3)﹣(+9)]﹣(﹣2)
(2)
(3)4﹣(+3.85)﹣(﹣3)+(﹣3.15)
(4)|3﹣4|+(﹣5﹣8)﹣|﹣1+5|﹣(5﹣20)
第二章2.7有理数的减法
参考答案与试题解析
一.选择题(共8小题)
1.如果崇左市市区某中午的气温是37℃,到下午下降了3℃,那么下午的气温是( )
A.40℃ B.38℃ C.36℃ D.34℃
考点:-有理数的减法.
专题:-应用题.
分析:-用中午的温度减去下降的温度,然后根据有理数的减法运算法则进行计算即可得解.
解答:-解:37℃﹣3℃=34℃.
故选:D.
点评:-本题考查了有理数的减法,是基础题,熟记运算法则是解题的关键.
2.哈市某天的最高气温为28℃,最低气温为21℃,则这一天的最高气温与最低气温的差为( )
A.5℃ B.6℃ C.7℃ D.8℃
考点:-有理数的减法.
专题:-常规题型.
分析:-根据有理数的减法,减去一个数等于加上这个数的相反数,可得答案.
解答:-解:28﹣21=28+(﹣21)=7,
故选:C.
点评:-本题考查了有理数的减法,减去一个数等于加上这个数的相反数.
3.下列各数中,比﹣2小1的是( )
A.﹣1 B.0 C.﹣3 D.3
考点:-有理数的减法.
专题:-计算题.
分析:-用﹣2减去1,然后根据减去一个是等于加上这个数的相反数计算即可得解.
解答:-解:﹣2﹣1=﹣3.
故选C.
点评:-本题考查了有理数的减法运算,熟练掌握减去一个是等于加上这个数的相反数是解题的关键,注意符号的处理.
4.计算(﹣3)﹣(﹣9)的结果等于( )
A.12 B.﹣12 C.6 D.﹣6
考点:-有理数的减法.
分析:-根据减去一个数等于加上这个数相反数,可得答案.
解答:-解:原式=(﹣3)+9
=(9﹣3)
=6,
故选:C.
点评:-本题考查了有理数的加法,先转化成加法,再进行加法运算.
5.﹣2013﹣2014的值为( )
A.1 B.4027 C.﹣4027 D.﹣1
考点:-有理数的减法.
分析:-根据有理数的减法运算法则进行计算即可得解.
解答:-解:﹣2013﹣2014=﹣4027.
故选C.
点评:-本题考查了有理数的减法运算,是基础题,熟记运算法则是解题的关键.
6.石家庄某市的最高气温是1℃,最低气温是﹣3℃,该天的温差是( )
A.2℃ B.3℃ C.4℃ D.5℃
考点:-有理数的减法.
分析:-用最高温度减去最低温度,然后根据减去一个数等于加上这个数的相反数进行计算即可得解.
解答:-解:1﹣(﹣3)
=1+3
=4℃.
故选C.
点评:-本题考查了有理数的减法,是基础题,熟记减去一个数等于加上这个数的相反数是解题的关键.
7.气温由﹣1℃下降5℃后是( )
A.﹣5℃ B.4℃ C.﹣4℃ D.﹣6℃
考点:-有理数的减法.
分析:-用﹣1减去5,然后根据有理数的减法运算法则进行计算即可得解.
解答:-解:﹣1﹣5=﹣6℃.
故选D.
点评:-本题考查了有理数的减法,是基础题,熟记运算法则是解题的关键.
8.计算,正确的结果为( )
A. B. C. D.
考点:-有理数的减法.
分析:-根据有理数的减法运算法则进行计算即可得解.
解答:-解:﹣=﹣.
故选D.
点评:-本题考查了有理数的减法运算是基础题,熟记法则是解题的关键.
二.填空题(共6小题)
9.计算:2000﹣2015= ﹣15 .
考点:-有理数的减法.
专题:-计算题.
分析:-根据有理数的减法运算进行计算即可得解.
解答:-解:2000﹣2015=﹣15.
故答案为:﹣15.
点评:-本题考查了有理数的减法,是基础题,熟记运算法则是解题的关键.
10.若x=4,则|x﹣5|= 1 .
考点:-有理数的减法;绝对值.
分析:-若x=4,则x﹣5=﹣1<0,由绝对值的定义:一个负数的绝对值是它的相反数,可得|x﹣5|的值.
解答:-解:∵x=4,∴x﹣5=﹣1<0,故|x﹣5|=|﹣1|=1.
点评:-本题考查绝对值的定义:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0;互为相反数的绝对值相等.
11.定义运算,则(﹣2) (﹣3)= ﹣2 .
考点:-有理数的减法;有理数大小比较.
专题:-新定义.
分析:-先根据减去一个数等于加上这个数的相反数求出﹣2﹣(﹣3),再根据新定义解答.
解答:-解:∵﹣2﹣(﹣3)=﹣2+3=1,
∴(﹣2) (﹣3)=﹣2.
故答案为:﹣2.
点评:-本题考查了有理数的减法,熟记减去一个数等于加上这个数的相反数是解题的关键,还要弄明白新定义的运算规则.
12.月球表面温度,中午是101℃,半夜是﹣150℃,则半夜比中午低 251 ℃.
考点:-有理数的减法.
分析:-用中午的温度减去半夜的温度,然后根据有理数的减法运算法则,减去一个数等于加上这个数的相反数计算即可得解.
解答:-解:101﹣(﹣150),
=101+150,
=251℃.
故答案为:251.
点评:-本题考查了有理数的减法,熟记减去一个数等于加上这个数的相反数是解题的关键.
13.计算:﹣|﹣2|= ﹣ .
考点:-有理数的减法;绝对值.
分析:-根据绝对值的性质去掉绝对值号,然后根据有理数的减法运算,减去一个数等于加上这个数的相反数进行计算即可得解.
解答:-解:﹣|﹣2|
=﹣2
=﹣.
故答案为:﹣.
点评:-本题考查了有理数的减法运算,绝对值的性质,是基础题,比较简单.
14.一只温度计刻度均匀但示数不准,将它放 ( http: / / www.21cnjy.com )入沸水中,示数为95摄氏度,放在冰水混合物中示数为﹣5摄氏度,当它的示数为32摄氏度时,实际温度是 37 ℃.
考点:-有理数的减法.
专题:-计算题.
分析:-先算出实际温度与标准温度间的温差,再求出当它的示数为32摄氏度时,实际温度是多少即可.
解答:-解:∵将它放入沸水中,示数为95摄氏度,放在冰水混合物中示数为﹣5摄氏度,
沸水的实际温度是100℃,
∴温差为100﹣95=5℃,
∴当它的示数为32摄氏度时,实际温度是32℃+5℃=37℃,
故答案为:37℃.
点评:-本题只要是考查了温差的概念,以及有理数的减法,是一个基础的题目.
三.解答题(共7小题)
15.计算:(﹣)﹣(﹣1)﹣(﹣1)﹣(+1.75).
考点:-有理数的减法.
分析:-根据减去一个数等于加上这个数的相反数,加法的交换律和结合律进行计算即可得解.
解答:-解:(﹣)﹣(﹣1)﹣(﹣1)﹣(+1.75)
=﹣+1+1﹣1.75
=1.
点评:-本题考查了有理数的减法,熟记减去一个数等于加上这个数的相反数是解题的关键,利用运算定律可以使计算更加简便.
16.用有理数的加法律计算:[(﹣72)﹣(﹣35)]﹣[(﹣23)﹣8].
考点:-有理数的减法.
分析:-可以先把括号省略,然后再利用有理数的加法交换律和结合律进行计算即可.
解答:-解:[(﹣72)﹣(﹣35)]﹣[(﹣23)﹣8]
=(﹣72+35)﹣(﹣23﹣8)
=﹣72+35+23+8
=35+23+8﹣72
=66﹣72
=﹣6.
点评:-本题主要考查有理数的加减混合运算,注意省略括号后的写法,容易出错.
17.若|a|=3,|b|=5,求a﹣b的值.
考点:-有理数的减法;绝对值.
专题:-分类讨论.
分析:-根据绝对值的意义,可得a、b的值,根据有理数的减法,可得答案.
解答:-解:若|a|=3,|b|=5,得
a=±3,b=±5.
当a=3,b=5时,a﹣b=3﹣5=3+(﹣5)=﹣2;
当a=3,b=﹣5时,a﹣b=3﹣(﹣5)=3+5=8;
当a=﹣3,b=5时,a﹣b=﹣3﹣5=﹣3+(﹣5)=﹣8;
当a=﹣3,b=﹣5时,a﹣b=﹣3﹣(﹣5)=﹣3+(+5)=2;
综上所述:a﹣b=±2,或a﹣b=±8.
点评:-本题考查了有理数的减法,利用绝对值的意义求出a、b的值,有理数的减法时要分类讨论.
18.计算:1﹣1﹣2﹣3﹣4﹣5﹣6﹣7﹣8﹣9﹣10﹣…﹣1009.
考点:-有理数的减法.
专题:-计算题.
分析:-根据有理数的减法运算法则,从第二个数开始,利用求和公式计算,然后解答即可.
解答:-解:1﹣1﹣2﹣3﹣4﹣5﹣6﹣7﹣8﹣9﹣10﹣…﹣1009
=1﹣(1+2+3+4+5+6+7+8+9+10+…+1009)
=1﹣
=1﹣509545
=﹣509544.
点评:-本题考查了有理数的减法,熟记运算法则和求和公式是解题的关键.
19.若|a|=5,|b|=3,(1)求a+b的值;(2)若|a+b|=a+b,求a﹣b的值.
考点:-有理数的减法;绝对值.
分析:-(1)由|a|=5,|b|=3可得,a=±5,b=±3,可分为4种情况求解;
(2)由|a+b|=a+b可得,a=5,b=3或a=5,b=﹣3,代入计算即可.
解答:-解:(1)∵|a|=5,|b|=3,
∴a=±5,b=±3,
当a=5,b=3时,a+b=8;
当a=5,b=﹣3时,a+b=2;
当a=﹣5,b=3时,a+b=﹣2;
当a=﹣5,b=﹣3时,a+b=﹣8.
(2)由|a+b|=a+b可得,a=5,b=3或a=5,b=﹣3.
当a=5,b=3时,a﹣b=2,
当a=5,b=﹣3时,a﹣b=8.
点评:-此题主要用了分类讨论的方法,各种情况都有考虑,不能遗漏.
20.(﹣)﹣(﹣3)﹣(﹣2)﹣(+5)
考点:-有理数的减法.
专题:-计算题.
分析:-先根据有理数的减法运算法则省略括号,再利用加法交换律和结合律进行计算即可得解.
解答:-解:(﹣)﹣(﹣3)﹣(﹣2)﹣(+5),
=﹣+3+2﹣5,
=﹣﹣5+3+2,
=﹣6+6,
=0.
点评:-本题考查了有理数的减法,有理数的加法,利用运算定律可以使计算更加简便.
21.加减混合运算
(1)[(﹣3)﹣(+9)]﹣(﹣2)
(2)
(3)4﹣(+3.85)﹣(﹣3)+(﹣3.15)
(4)|3﹣4|+(﹣5﹣8)﹣|﹣1+5|﹣(5﹣20)
考点:-有理数的减法.
专题:-计算题.
分析:-(1)先省略括号,再根据有理数的减法运算法则进行计算即可得解;
(2)先统一成有理数的加法运算,再把同分母的分数进行计算;
(3)把带分数和带分数,小数和小数交换结合到一起,然后进行计算即可得解;
(4)先去掉绝对值号并计算括号里面的,再根据有理数的加法和减法运算法则进行计算即可得解.
解答:-解:(1)[(﹣3)﹣(+9)]﹣(﹣2)
=(﹣3﹣9)+2
=﹣12+2
=﹣10;
(2)(﹣)﹣(+)﹣(﹣)﹣(+)﹣(+1)
=﹣﹣+﹣﹣1
=﹣1+﹣2
=﹣2;
(3)4﹣(+3.85)﹣(﹣3)+(﹣3.15)
=4+3﹣3.85﹣3.15
=8.5﹣7
=1.5;
(4)|3﹣4|+(﹣5﹣8)﹣|﹣1+5|﹣(5﹣20)
=1﹣13﹣4+15
=16﹣17
=﹣1.
点评:-本题考查了有理数的加减混合运算,绝对值的性质,熟记运算法则是解题的关键,利用加法交换律结合律可以使计算更加简便.
农安县合隆中学 徐亚惠
一.选择题(共8小题)
1.如果崇左市市区某中午的气温是37℃,到下午下降了3℃,那么下午的气温是( )
A.40℃ B.38℃ C.36℃ D.34℃
2.哈市某天的最高气温为28℃,最低气温为21℃,则这一天的最高气温与最低气温的差为( )
A.5℃ B.6℃ C.7℃ D.8℃
3.下列各数中,比﹣2小1的是( )
A.﹣1 B.0 C.﹣3 D.3
4.计算(﹣3)﹣(﹣9)的结果等于( )
A.12 B.﹣12 C.6 D.﹣6
5.﹣2013﹣2014的值为( )
A.1 B.4027 C.﹣4027 D.﹣1
6.石家庄某市的最高气温是1℃,最低气温是﹣3℃,该天的温差是( )
A.2℃ B.3℃ C.4℃ D.5℃
7.气温由﹣1℃下降5℃后是( )
A.﹣5℃ B.4℃ C.﹣4℃ D.﹣6℃
8.计算,正确的结果为( )
A. B. C. D.
二.填空题(共6小题)
9.计算:2000﹣2015= _________ .
10.若x=4,则|x﹣5|= _________ .
11.定义运算,则(﹣2) (﹣3)= _________ .
12.月球表面温度,中午是101℃,半夜是﹣150℃,则半夜比中午低 _________ ℃.
13.计算:﹣|﹣2|= _________ .
14.一只温度计刻度均匀但示数不准,将它放 ( http: / / www.21cnjy.com )入沸水中,示数为95摄氏度,放在冰水混合物中示数为﹣5摄氏度,当它的示数为32摄氏度时,实际温度是 _________ ℃.
三.解答题(共7小题)
15.计算:(﹣)﹣(﹣1)﹣(﹣1)﹣(+1.75).
16.用有理数的加法律计算:[(﹣72)﹣(﹣35)]﹣[(﹣23)﹣8].
17.若|a|=3,|b|=5,求a﹣b的值.
18.计算:1﹣1﹣2﹣3﹣4﹣5﹣6﹣7﹣8﹣9﹣10﹣…﹣1009.
19.若|a|=5,|b|=3,(1)求a+b的值;(2)若|a+b|=a+b,求a﹣b的值.
20.(﹣)﹣(﹣3)﹣(﹣2)﹣(+5)
21.加减混合运算
(1)[(﹣3)﹣(+9)]﹣(﹣2)
(2)
(3)4﹣(+3.85)﹣(﹣3)+(﹣3.15)
(4)|3﹣4|+(﹣5﹣8)﹣|﹣1+5|﹣(5﹣20)
第二章2.7有理数的减法
参考答案与试题解析
一.选择题(共8小题)
1.如果崇左市市区某中午的气温是37℃,到下午下降了3℃,那么下午的气温是( )
A.40℃ B.38℃ C.36℃ D.34℃
考点:-有理数的减法.
专题:-应用题.
分析:-用中午的温度减去下降的温度,然后根据有理数的减法运算法则进行计算即可得解.
解答:-解:37℃﹣3℃=34℃.
故选:D.
点评:-本题考查了有理数的减法,是基础题,熟记运算法则是解题的关键.
2.哈市某天的最高气温为28℃,最低气温为21℃,则这一天的最高气温与最低气温的差为( )
A.5℃ B.6℃ C.7℃ D.8℃
考点:-有理数的减法.
专题:-常规题型.
分析:-根据有理数的减法,减去一个数等于加上这个数的相反数,可得答案.
解答:-解:28﹣21=28+(﹣21)=7,
故选:C.
点评:-本题考查了有理数的减法,减去一个数等于加上这个数的相反数.
3.下列各数中,比﹣2小1的是( )
A.﹣1 B.0 C.﹣3 D.3
考点:-有理数的减法.
专题:-计算题.
分析:-用﹣2减去1,然后根据减去一个是等于加上这个数的相反数计算即可得解.
解答:-解:﹣2﹣1=﹣3.
故选C.
点评:-本题考查了有理数的减法运算,熟练掌握减去一个是等于加上这个数的相反数是解题的关键,注意符号的处理.
4.计算(﹣3)﹣(﹣9)的结果等于( )
A.12 B.﹣12 C.6 D.﹣6
考点:-有理数的减法.
分析:-根据减去一个数等于加上这个数相反数,可得答案.
解答:-解:原式=(﹣3)+9
=(9﹣3)
=6,
故选:C.
点评:-本题考查了有理数的加法,先转化成加法,再进行加法运算.
5.﹣2013﹣2014的值为( )
A.1 B.4027 C.﹣4027 D.﹣1
考点:-有理数的减法.
分析:-根据有理数的减法运算法则进行计算即可得解.
解答:-解:﹣2013﹣2014=﹣4027.
故选C.
点评:-本题考查了有理数的减法运算,是基础题,熟记运算法则是解题的关键.
6.石家庄某市的最高气温是1℃,最低气温是﹣3℃,该天的温差是( )
A.2℃ B.3℃ C.4℃ D.5℃
考点:-有理数的减法.
分析:-用最高温度减去最低温度,然后根据减去一个数等于加上这个数的相反数进行计算即可得解.
解答:-解:1﹣(﹣3)
=1+3
=4℃.
故选C.
点评:-本题考查了有理数的减法,是基础题,熟记减去一个数等于加上这个数的相反数是解题的关键.
7.气温由﹣1℃下降5℃后是( )
A.﹣5℃ B.4℃ C.﹣4℃ D.﹣6℃
考点:-有理数的减法.
分析:-用﹣1减去5,然后根据有理数的减法运算法则进行计算即可得解.
解答:-解:﹣1﹣5=﹣6℃.
故选D.
点评:-本题考查了有理数的减法,是基础题,熟记运算法则是解题的关键.
8.计算,正确的结果为( )
A. B. C. D.
考点:-有理数的减法.
分析:-根据有理数的减法运算法则进行计算即可得解.
解答:-解:﹣=﹣.
故选D.
点评:-本题考查了有理数的减法运算是基础题,熟记法则是解题的关键.
二.填空题(共6小题)
9.计算:2000﹣2015= ﹣15 .
考点:-有理数的减法.
专题:-计算题.
分析:-根据有理数的减法运算进行计算即可得解.
解答:-解:2000﹣2015=﹣15.
故答案为:﹣15.
点评:-本题考查了有理数的减法,是基础题,熟记运算法则是解题的关键.
10.若x=4,则|x﹣5|= 1 .
考点:-有理数的减法;绝对值.
分析:-若x=4,则x﹣5=﹣1<0,由绝对值的定义:一个负数的绝对值是它的相反数,可得|x﹣5|的值.
解答:-解:∵x=4,∴x﹣5=﹣1<0,故|x﹣5|=|﹣1|=1.
点评:-本题考查绝对值的定义:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0;互为相反数的绝对值相等.
11.定义运算,则(﹣2) (﹣3)= ﹣2 .
考点:-有理数的减法;有理数大小比较.
专题:-新定义.
分析:-先根据减去一个数等于加上这个数的相反数求出﹣2﹣(﹣3),再根据新定义解答.
解答:-解:∵﹣2﹣(﹣3)=﹣2+3=1,
∴(﹣2) (﹣3)=﹣2.
故答案为:﹣2.
点评:-本题考查了有理数的减法,熟记减去一个数等于加上这个数的相反数是解题的关键,还要弄明白新定义的运算规则.
12.月球表面温度,中午是101℃,半夜是﹣150℃,则半夜比中午低 251 ℃.
考点:-有理数的减法.
分析:-用中午的温度减去半夜的温度,然后根据有理数的减法运算法则,减去一个数等于加上这个数的相反数计算即可得解.
解答:-解:101﹣(﹣150),
=101+150,
=251℃.
故答案为:251.
点评:-本题考查了有理数的减法,熟记减去一个数等于加上这个数的相反数是解题的关键.
13.计算:﹣|﹣2|= ﹣ .
考点:-有理数的减法;绝对值.
分析:-根据绝对值的性质去掉绝对值号,然后根据有理数的减法运算,减去一个数等于加上这个数的相反数进行计算即可得解.
解答:-解:﹣|﹣2|
=﹣2
=﹣.
故答案为:﹣.
点评:-本题考查了有理数的减法运算,绝对值的性质,是基础题,比较简单.
14.一只温度计刻度均匀但示数不准,将它放 ( http: / / www.21cnjy.com )入沸水中,示数为95摄氏度,放在冰水混合物中示数为﹣5摄氏度,当它的示数为32摄氏度时,实际温度是 37 ℃.
考点:-有理数的减法.
专题:-计算题.
分析:-先算出实际温度与标准温度间的温差,再求出当它的示数为32摄氏度时,实际温度是多少即可.
解答:-解:∵将它放入沸水中,示数为95摄氏度,放在冰水混合物中示数为﹣5摄氏度,
沸水的实际温度是100℃,
∴温差为100﹣95=5℃,
∴当它的示数为32摄氏度时,实际温度是32℃+5℃=37℃,
故答案为:37℃.
点评:-本题只要是考查了温差的概念,以及有理数的减法,是一个基础的题目.
三.解答题(共7小题)
15.计算:(﹣)﹣(﹣1)﹣(﹣1)﹣(+1.75).
考点:-有理数的减法.
分析:-根据减去一个数等于加上这个数的相反数,加法的交换律和结合律进行计算即可得解.
解答:-解:(﹣)﹣(﹣1)﹣(﹣1)﹣(+1.75)
=﹣+1+1﹣1.75
=1.
点评:-本题考查了有理数的减法,熟记减去一个数等于加上这个数的相反数是解题的关键,利用运算定律可以使计算更加简便.
16.用有理数的加法律计算:[(﹣72)﹣(﹣35)]﹣[(﹣23)﹣8].
考点:-有理数的减法.
分析:-可以先把括号省略,然后再利用有理数的加法交换律和结合律进行计算即可.
解答:-解:[(﹣72)﹣(﹣35)]﹣[(﹣23)﹣8]
=(﹣72+35)﹣(﹣23﹣8)
=﹣72+35+23+8
=35+23+8﹣72
=66﹣72
=﹣6.
点评:-本题主要考查有理数的加减混合运算,注意省略括号后的写法,容易出错.
17.若|a|=3,|b|=5,求a﹣b的值.
考点:-有理数的减法;绝对值.
专题:-分类讨论.
分析:-根据绝对值的意义,可得a、b的值,根据有理数的减法,可得答案.
解答:-解:若|a|=3,|b|=5,得
a=±3,b=±5.
当a=3,b=5时,a﹣b=3﹣5=3+(﹣5)=﹣2;
当a=3,b=﹣5时,a﹣b=3﹣(﹣5)=3+5=8;
当a=﹣3,b=5时,a﹣b=﹣3﹣5=﹣3+(﹣5)=﹣8;
当a=﹣3,b=﹣5时,a﹣b=﹣3﹣(﹣5)=﹣3+(+5)=2;
综上所述:a﹣b=±2,或a﹣b=±8.
点评:-本题考查了有理数的减法,利用绝对值的意义求出a、b的值,有理数的减法时要分类讨论.
18.计算:1﹣1﹣2﹣3﹣4﹣5﹣6﹣7﹣8﹣9﹣10﹣…﹣1009.
考点:-有理数的减法.
专题:-计算题.
分析:-根据有理数的减法运算法则,从第二个数开始,利用求和公式计算,然后解答即可.
解答:-解:1﹣1﹣2﹣3﹣4﹣5﹣6﹣7﹣8﹣9﹣10﹣…﹣1009
=1﹣(1+2+3+4+5+6+7+8+9+10+…+1009)
=1﹣
=1﹣509545
=﹣509544.
点评:-本题考查了有理数的减法,熟记运算法则和求和公式是解题的关键.
19.若|a|=5,|b|=3,(1)求a+b的值;(2)若|a+b|=a+b,求a﹣b的值.
考点:-有理数的减法;绝对值.
分析:-(1)由|a|=5,|b|=3可得,a=±5,b=±3,可分为4种情况求解;
(2)由|a+b|=a+b可得,a=5,b=3或a=5,b=﹣3,代入计算即可.
解答:-解:(1)∵|a|=5,|b|=3,
∴a=±5,b=±3,
当a=5,b=3时,a+b=8;
当a=5,b=﹣3时,a+b=2;
当a=﹣5,b=3时,a+b=﹣2;
当a=﹣5,b=﹣3时,a+b=﹣8.
(2)由|a+b|=a+b可得,a=5,b=3或a=5,b=﹣3.
当a=5,b=3时,a﹣b=2,
当a=5,b=﹣3时,a﹣b=8.
点评:-此题主要用了分类讨论的方法,各种情况都有考虑,不能遗漏.
20.(﹣)﹣(﹣3)﹣(﹣2)﹣(+5)
考点:-有理数的减法.
专题:-计算题.
分析:-先根据有理数的减法运算法则省略括号,再利用加法交换律和结合律进行计算即可得解.
解答:-解:(﹣)﹣(﹣3)﹣(﹣2)﹣(+5),
=﹣+3+2﹣5,
=﹣﹣5+3+2,
=﹣6+6,
=0.
点评:-本题考查了有理数的减法,有理数的加法,利用运算定律可以使计算更加简便.
21.加减混合运算
(1)[(﹣3)﹣(+9)]﹣(﹣2)
(2)
(3)4﹣(+3.85)﹣(﹣3)+(﹣3.15)
(4)|3﹣4|+(﹣5﹣8)﹣|﹣1+5|﹣(5﹣20)
考点:-有理数的减法.
专题:-计算题.
分析:-(1)先省略括号,再根据有理数的减法运算法则进行计算即可得解;
(2)先统一成有理数的加法运算,再把同分母的分数进行计算;
(3)把带分数和带分数,小数和小数交换结合到一起,然后进行计算即可得解;
(4)先去掉绝对值号并计算括号里面的,再根据有理数的加法和减法运算法则进行计算即可得解.
解答:-解:(1)[(﹣3)﹣(+9)]﹣(﹣2)
=(﹣3﹣9)+2
=﹣12+2
=﹣10;
(2)(﹣)﹣(+)﹣(﹣)﹣(+)﹣(+1)
=﹣﹣+﹣﹣1
=﹣1+﹣2
=﹣2;
(3)4﹣(+3.85)﹣(﹣3)+(﹣3.15)
=4+3﹣3.85﹣3.15
=8.5﹣7
=1.5;
(4)|3﹣4|+(﹣5﹣8)﹣|﹣1+5|﹣(5﹣20)
=1﹣13﹣4+15
=16﹣17
=﹣1.
点评:-本题考查了有理数的加减混合运算,绝对值的性质,熟记运算法则是解题的关键,利用加法交换律结合律可以使计算更加简便.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
