2023-2024学年高中数学人教A版2019 选择性必修第三册 第七章 随机变量及其分布 培优课——离散型随机变量的均值与方差的综合应用(含解析)
文档属性
| 名称 | 2023-2024学年高中数学人教A版2019 选择性必修第三册 第七章 随机变量及其分布 培优课——离散型随机变量的均值与方差的综合应用(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 61.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-28 16:15:13 | ||
图片预览



文档简介
培优课——离散型随机变量的均值与方差的综合应用
A级 必备知识基础练
1.已知随机变量ξi满足P(ξi=1)=pi,P(ξi=0)=1-pi,i=1,2.若0A.E(ξ1)B.E(ξ1)D(ξ2)
C.E(ξ1)>E(ξ2),D(ξ1)D.E(ξ1)>E(ξ2),D(ξ1)>D(ξ2)
2.甲、乙两台自动车床生产同种标准的零件,X表示甲车床生产1 000件产品中的次品数,Y表示乙车床生产1 000件产品中的次品数,经过一段时间的考察,X,Y的分布列分别为
X 0 1 2 3
P 0.7 0.1 0.1 0.1
Y 0 1 2
P 0.5 0.3 0.2
据此判定( )
A.甲生产的零件质量比乙生产的零件质量好
B.乙生产的零件质量比甲生产的零件质量好
C.甲生产的零件质量与乙生产的零件质量一样
D.无法判定
3.已知随机变量X的分布列为P(X=k)=,k=3,6,9,则D(X)等于( )
A.6 B.9 C.3 D.4
4.(2022重庆九龙坡月考)学校要从10名候选人中选2名同学组成学生会,其中高二(1)班有4名候选人,假设每名候选人都有相同的机会被选到,若X表示选到高二(1)班的候选人的人数,则E(X)=( )
A. B. C. D.
5.小芳用肢体语言把成语的意思传递给本组其他同学.若小组内同学甲猜对成语的概率是0.4,同学乙猜对成语的概率是0.5,且规定猜对得1分,猜不对得0分,则这两个同学各猜1次,得分之和X(单位:分)的均值为( )
A.0.9 B.0.8 C.1.2 D.1.1
6.同时抛掷两枚质地均匀的骰子,至少有一个3点或6点出现时,就说这次试验成功,则在9次试验中,成功次数X的均值是 .
7.若随机事件A在1次试验中发生的概率为p(08.某陶瓷厂准备烧制甲、乙、丙三件不同的工艺品,制作过程必须先后经过两次烧制,当第一次烧制合格后方可进入第二次烧制,两次烧制过程相互独立.根据该厂现有的技术水平,经过第一次烧制后,甲、乙、丙三件产品合格的概率依次为0.5,0.6,0.4.经过第二次烧制后,甲、乙、丙三件产品合格的概率依次为0.6,0.5,0.75.
(1)求第一次烧制后恰有一件产品合格的概率;
(2)经过前后两次烧制后,合格工艺品的个数为ξ,求随机变量ξ的均值与方差.
B级 关键能力提升练
9.某城市有甲、乙、丙3个旅游景点,一位客人游览这三个景点的概率分别是0.4,0.5,0.6,且此人是否游览哪个景点互不影响,设X表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值,则E(X)等于( )
A.1.48 B.0.76 C.0.24 D.1
10.随机变量X的分布列如下.
X 1 2 3
P x y
若E(X)=,则D(X)等于( )
A. B. C. D.
11.若随机变量X满足P{X=m}=(m=1,2,…,N),N为正整数,则当N >100时,的值最接近( )
A.0 B. C. D.1
12.已知在10件产品中可能存在次品,从中抽取2件检查,其次品数为ξ,已知P(ξ=1)=且该产品的次品率不超过40%,则这10件产品的次品率为( )
A.10% B.20% C.30% D.40%
13.已知离散型随机变量ξ的可能值为-1,0,1,且E(ξ)=0.1,D(ξ)=0.89,则对应的概率P1(X=-1),P2(X=0),P3(X=1)分别为 、 、 .
14.一个篮球运动员投篮一次得3分的概率为a,得2分的概率为b,不得分的概率为c(a,b,c∈(0,1)),已知他投篮一次得分的均值为1(不计其他得分情况),则ab的最大值为 .
15.
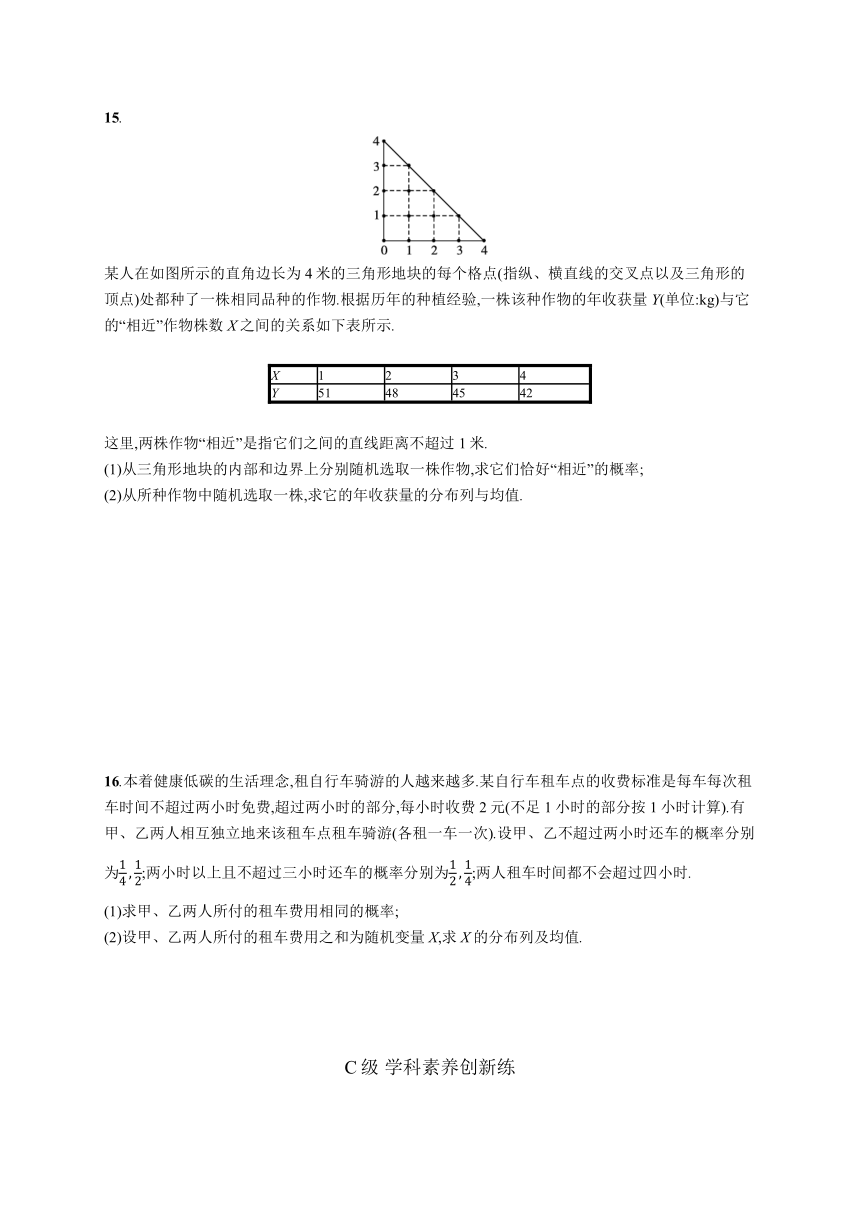
某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获量Y(单位:kg)与它的“相近”作物株数X之间的关系如下表所示.
X 1 2 3 4
Y 51 48 45 42
这里,两株作物“相近”是指它们之间的直线距离不超过1米.
(1)从三角形地块的内部和边界上分别随机选取一株作物,求它们恰好“相近”的概率;
(2)从所种作物中随机选取一株,求它的年收获量的分布列与均值.
16.本着健康低碳的生活理念,租自行车骑游的人越来越多.某自行车租车点的收费标准是每车每次租车时间不超过两小时免费,超过两小时的部分,每小时收费2元(不足1小时的部分按1小时计算).有甲、乙两人相互独立地来该租车点租车骑游(各租一车一次).设甲、乙不超过两小时还车的概率分别为;两小时以上且不超过三小时还车的概率分别为;两人租车时间都不会超过四小时.
(1)求甲、乙两人所付的租车费用相同的概率;
(2)设甲、乙两人所付的租车费用之和为随机变量X,求X的分布列及均值.
C级 学科素养创新练
17.(2022北京丰台一模)为研究某地区2021届大学毕业生毕业三个月后的毕业去向,某调查公司从该地区2021届大学毕业生中随机选取了1 000人作为样本进行调查,结果如下:
毕业 去向 继续学 习深造 单位 就业 自主 创业 自由 职业 慢就业
人数 200 560 14 128 98
假设该地区2021届大学毕业生选择的毕业去向相互独立.
(1)若该地区一所高校2021届大学毕业生的人数为2 500,试根据样本估计该校2021届大学毕业生选择“单位就业”的人数;
(2)从该地区2021届大学毕业生中随机选取3人,记随机变量X为这3人中选择“继续学习深造”的人数,以样本的频率估计概率,求X的分布列和数学期望E(X);
(3)该公司在半年后对样本中的毕业生进行再调查,发现仅有选择“慢就业”的毕业生中的a(0培优课——离散型随机变量的均值与方差的综合应用
1.A 由题意可知ξi(i=1,2)服从两点分布,
∴E(ξ1)=p1,E(ξ2)=p2,D(ξ1)=p1(1-p1),D(ξ2)=p2(1-p2),
又0故由题意可知,D(ξ1)2.A E(X)=0×0.7+1×0.1+2×0.1+3×0.1=0.6,E(Y)=0×0.5+1×0.3+2×0.2=0.7.
显然E(X)3.A E(X)=3+6+9=6.
D(X)=(3-6)2+(6-6)2+(9-6)2=6.
4.D X的可能取值有0,1,2,
且P(X=0)=,P(X=1)=,P(X=2)=,
X的分布列如下:
X 0 1 2
P
E(X)=0+1+2
5.A 由题意得X=0,1,2,则P(X=0)=0.6×0.5=0.3,P(X=1)=0.4×0.5+0.6×0.5=0.5,P(X=2)=0.4×0.5=0.2,故E(X)=1×0.5+2×0.2=0.9.
6.5 由已知,同时抛掷两枚骰子一次,至少有一个3点或6点出现时的概率为,
9次试验相当于9次独立重复试验,则成功次数X服从二项分布,即X~B
故E(X)=9=5.
7 随机变量X的所有可能的取值是0,1,并且P(X=1)=p,P(X=0)=1-p.
从而E(X)=0×(1-p)+1×p=p.
D(X)=(0-p)2×(1-p)+(1-p)2·p=p-p2=
因为08.解分别记甲、乙、丙经第一次烧制后合格为事件A1,A2,A3.
(1)设E表示第一次烧制后恰好有一件合格,则
P(E)=P(A1)+P(A2)+P(A3)=0.5×0.4×0.6+0.5×0.6×0.6+0.5×0.4×0.4=0.38.
(2)因为每件工艺品经过两次烧制后合格的概率均为p=0.3,所以ξ~B(3,0.3).
所以E(ξ)=np=3×0.3=0.9,D(ξ)=np(1-p)=3×0.3×0.7=0.63.
9.A X的分布列为
X 1 3
P 0.76 0.24
E(X)=1×0.76+3×0.24=1.48.
10.D 由
所以D(X)=1-2+2-2+3-2
11.C 由题意可知,E(X)=mP{X=m}=,
显然,当N>100时,的值最接近
12.B 设10件产品中存在n件次品,从中抽取2件,其次品数为ξ,由P(ξ=1)=,得,化简得n2-10n+16=0,解得n=2或n=8.又该产品的次品率不超过40%,则n≤4,即n=2,则这10件产品的次品率为=20%.
13.0.4 0.1 0.5 ξ的分布列为
ξ -1 0 1
P P1 P2 P3
E(ξ)=-P1+P3=0.1,
D(ξ)=(-1-0.1)2P1+(0-0.1)2P2+(1-0.1)2P3=0.89.
即1.21P1+0.01P2+0.81P3=0.89,
即121P1+P2+81P3=89.
又P1+P2+P3=1,
解得
14 由已知可得3a+2b+0×c=1,
即3a+2b=1,
故ab=3a·2b
当且仅当3a=2b=时取等号,即ab的最大值为
15.解(1)所种作物总株数N=1+2+3+4+5=15,其中三角形地块内部的作物株数为3,边界上的作物株数为12.从三角形地块的内部和边界上分别随机选取一株的不同结果有=36(种),选取的两株作物恰好“相近”的不同结果有3+3+2=8(种).故从三角形地块的内部和边界上分别随机选取一株作物,它们恰好“相近”的概率为
(2)先求从所种作物中随机选取一株作物的年收获量Y的分布列.
因为P(Y=51)=P(X=1),P(Y=48)=P(X=2),P(Y=45)=P(X=3),P(Y=42)=P(X=4),
所以只需求出P(X=k)(k=1,2,3,4)即可.
记nk为其“相近”作物恰有k株的作物株数(k=1,2,3,4),则n1=2,n2=4,n3=6,n4=3.
由P(X=k)=得P(X=1)=,
P(X=2)=,P(X=3)=,
P(X=4)=
故所求的分布列为
Y 51 48 45 42
P
E(Y)=51+48+45+42=46.
16.解(1)由题意得,甲、乙在三小时以上且不超过四小时还车的概率分别为记甲、乙两人所付的租车费用相同为事件A,
则P(A)=
故甲、乙两人所付的租车费用相同的概率为
(2)X的可能取值为0,2,4,6,8.
P(X=0)=,
P(X=2)=,
P(X=4)=,
P(X=6)=,
P(X=8)=
∴甲、乙两人所付的租车费用之和X的分布列为
X 0 2 4 6 8
P
∴E(X)=0+2+4+6+8
17.解 (1)由题意得,该校2021届大学毕业生选择“单位就业”的人数为2 500=1 400.
(2)由题意得,样本中1 000名毕业生选择“继续学习深造”的频率为
用频率估计概率,从该地区2021届大学毕业生中随机选取1名学生,估计该生选择“继续学习深造”的概率为
随机变量X的所有可能取值为0,1,2,3,
所以P(X=0)=01-3=,
P(X=1)=1-2=,
P(X=2)=21-=,
P(X=3)=31-0=,
所以X的分布列为
X 0 1 2 3
P
E(X)=0+1+2+3
A级 必备知识基础练
1.已知随机变量ξi满足P(ξi=1)=pi,P(ξi=0)=1-pi,i=1,2.若0
C.E(ξ1)>E(ξ2),D(ξ1)
2.甲、乙两台自动车床生产同种标准的零件,X表示甲车床生产1 000件产品中的次品数,Y表示乙车床生产1 000件产品中的次品数,经过一段时间的考察,X,Y的分布列分别为
X 0 1 2 3
P 0.7 0.1 0.1 0.1
Y 0 1 2
P 0.5 0.3 0.2
据此判定( )
A.甲生产的零件质量比乙生产的零件质量好
B.乙生产的零件质量比甲生产的零件质量好
C.甲生产的零件质量与乙生产的零件质量一样
D.无法判定
3.已知随机变量X的分布列为P(X=k)=,k=3,6,9,则D(X)等于( )
A.6 B.9 C.3 D.4
4.(2022重庆九龙坡月考)学校要从10名候选人中选2名同学组成学生会,其中高二(1)班有4名候选人,假设每名候选人都有相同的机会被选到,若X表示选到高二(1)班的候选人的人数,则E(X)=( )
A. B. C. D.
5.小芳用肢体语言把成语的意思传递给本组其他同学.若小组内同学甲猜对成语的概率是0.4,同学乙猜对成语的概率是0.5,且规定猜对得1分,猜不对得0分,则这两个同学各猜1次,得分之和X(单位:分)的均值为( )
A.0.9 B.0.8 C.1.2 D.1.1
6.同时抛掷两枚质地均匀的骰子,至少有一个3点或6点出现时,就说这次试验成功,则在9次试验中,成功次数X的均值是 .
7.若随机事件A在1次试验中发生的概率为p(0
(1)求第一次烧制后恰有一件产品合格的概率;
(2)经过前后两次烧制后,合格工艺品的个数为ξ,求随机变量ξ的均值与方差.
B级 关键能力提升练
9.某城市有甲、乙、丙3个旅游景点,一位客人游览这三个景点的概率分别是0.4,0.5,0.6,且此人是否游览哪个景点互不影响,设X表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值,则E(X)等于( )
A.1.48 B.0.76 C.0.24 D.1
10.随机变量X的分布列如下.
X 1 2 3
P x y
若E(X)=,则D(X)等于( )
A. B. C. D.
11.若随机变量X满足P{X=m}=(m=1,2,…,N),N为正整数,则当N >100时,的值最接近( )
A.0 B. C. D.1
12.已知在10件产品中可能存在次品,从中抽取2件检查,其次品数为ξ,已知P(ξ=1)=且该产品的次品率不超过40%,则这10件产品的次品率为( )
A.10% B.20% C.30% D.40%
13.已知离散型随机变量ξ的可能值为-1,0,1,且E(ξ)=0.1,D(ξ)=0.89,则对应的概率P1(X=-1),P2(X=0),P3(X=1)分别为 、 、 .
14.一个篮球运动员投篮一次得3分的概率为a,得2分的概率为b,不得分的概率为c(a,b,c∈(0,1)),已知他投篮一次得分的均值为1(不计其他得分情况),则ab的最大值为 .
15.
某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获量Y(单位:kg)与它的“相近”作物株数X之间的关系如下表所示.
X 1 2 3 4
Y 51 48 45 42
这里,两株作物“相近”是指它们之间的直线距离不超过1米.
(1)从三角形地块的内部和边界上分别随机选取一株作物,求它们恰好“相近”的概率;
(2)从所种作物中随机选取一株,求它的年收获量的分布列与均值.
16.本着健康低碳的生活理念,租自行车骑游的人越来越多.某自行车租车点的收费标准是每车每次租车时间不超过两小时免费,超过两小时的部分,每小时收费2元(不足1小时的部分按1小时计算).有甲、乙两人相互独立地来该租车点租车骑游(各租一车一次).设甲、乙不超过两小时还车的概率分别为;两小时以上且不超过三小时还车的概率分别为;两人租车时间都不会超过四小时.
(1)求甲、乙两人所付的租车费用相同的概率;
(2)设甲、乙两人所付的租车费用之和为随机变量X,求X的分布列及均值.
C级 学科素养创新练
17.(2022北京丰台一模)为研究某地区2021届大学毕业生毕业三个月后的毕业去向,某调查公司从该地区2021届大学毕业生中随机选取了1 000人作为样本进行调查,结果如下:
毕业 去向 继续学 习深造 单位 就业 自主 创业 自由 职业 慢就业
人数 200 560 14 128 98
假设该地区2021届大学毕业生选择的毕业去向相互独立.
(1)若该地区一所高校2021届大学毕业生的人数为2 500,试根据样本估计该校2021届大学毕业生选择“单位就业”的人数;
(2)从该地区2021届大学毕业生中随机选取3人,记随机变量X为这3人中选择“继续学习深造”的人数,以样本的频率估计概率,求X的分布列和数学期望E(X);
(3)该公司在半年后对样本中的毕业生进行再调查,发现仅有选择“慢就业”的毕业生中的a(0
1.A 由题意可知ξi(i=1,2)服从两点分布,
∴E(ξ1)=p1,E(ξ2)=p2,D(ξ1)=p1(1-p1),D(ξ2)=p2(1-p2),
又0
显然E(X)
D(X)=(3-6)2+(6-6)2+(9-6)2=6.
4.D X的可能取值有0,1,2,
且P(X=0)=,P(X=1)=,P(X=2)=,
X的分布列如下:
X 0 1 2
P
E(X)=0+1+2
5.A 由题意得X=0,1,2,则P(X=0)=0.6×0.5=0.3,P(X=1)=0.4×0.5+0.6×0.5=0.5,P(X=2)=0.4×0.5=0.2,故E(X)=1×0.5+2×0.2=0.9.
6.5 由已知,同时抛掷两枚骰子一次,至少有一个3点或6点出现时的概率为,
9次试验相当于9次独立重复试验,则成功次数X服从二项分布,即X~B
故E(X)=9=5.
7 随机变量X的所有可能的取值是0,1,并且P(X=1)=p,P(X=0)=1-p.
从而E(X)=0×(1-p)+1×p=p.
D(X)=(0-p)2×(1-p)+(1-p)2·p=p-p2=
因为0
(1)设E表示第一次烧制后恰好有一件合格,则
P(E)=P(A1)+P(A2)+P(A3)=0.5×0.4×0.6+0.5×0.6×0.6+0.5×0.4×0.4=0.38.
(2)因为每件工艺品经过两次烧制后合格的概率均为p=0.3,所以ξ~B(3,0.3).
所以E(ξ)=np=3×0.3=0.9,D(ξ)=np(1-p)=3×0.3×0.7=0.63.
9.A X的分布列为
X 1 3
P 0.76 0.24
E(X)=1×0.76+3×0.24=1.48.
10.D 由
所以D(X)=1-2+2-2+3-2
11.C 由题意可知,E(X)=mP{X=m}=,
显然,当N>100时,的值最接近
12.B 设10件产品中存在n件次品,从中抽取2件,其次品数为ξ,由P(ξ=1)=,得,化简得n2-10n+16=0,解得n=2或n=8.又该产品的次品率不超过40%,则n≤4,即n=2,则这10件产品的次品率为=20%.
13.0.4 0.1 0.5 ξ的分布列为
ξ -1 0 1
P P1 P2 P3
E(ξ)=-P1+P3=0.1,
D(ξ)=(-1-0.1)2P1+(0-0.1)2P2+(1-0.1)2P3=0.89.
即1.21P1+0.01P2+0.81P3=0.89,
即121P1+P2+81P3=89.
又P1+P2+P3=1,
解得
14 由已知可得3a+2b+0×c=1,
即3a+2b=1,
故ab=3a·2b
当且仅当3a=2b=时取等号,即ab的最大值为
15.解(1)所种作物总株数N=1+2+3+4+5=15,其中三角形地块内部的作物株数为3,边界上的作物株数为12.从三角形地块的内部和边界上分别随机选取一株的不同结果有=36(种),选取的两株作物恰好“相近”的不同结果有3+3+2=8(种).故从三角形地块的内部和边界上分别随机选取一株作物,它们恰好“相近”的概率为
(2)先求从所种作物中随机选取一株作物的年收获量Y的分布列.
因为P(Y=51)=P(X=1),P(Y=48)=P(X=2),P(Y=45)=P(X=3),P(Y=42)=P(X=4),
所以只需求出P(X=k)(k=1,2,3,4)即可.
记nk为其“相近”作物恰有k株的作物株数(k=1,2,3,4),则n1=2,n2=4,n3=6,n4=3.
由P(X=k)=得P(X=1)=,
P(X=2)=,P(X=3)=,
P(X=4)=
故所求的分布列为
Y 51 48 45 42
P
E(Y)=51+48+45+42=46.
16.解(1)由题意得,甲、乙在三小时以上且不超过四小时还车的概率分别为记甲、乙两人所付的租车费用相同为事件A,
则P(A)=
故甲、乙两人所付的租车费用相同的概率为
(2)X的可能取值为0,2,4,6,8.
P(X=0)=,
P(X=2)=,
P(X=4)=,
P(X=6)=,
P(X=8)=
∴甲、乙两人所付的租车费用之和X的分布列为
X 0 2 4 6 8
P
∴E(X)=0+2+4+6+8
17.解 (1)由题意得,该校2021届大学毕业生选择“单位就业”的人数为2 500=1 400.
(2)由题意得,样本中1 000名毕业生选择“继续学习深造”的频率为
用频率估计概率,从该地区2021届大学毕业生中随机选取1名学生,估计该生选择“继续学习深造”的概率为
随机变量X的所有可能取值为0,1,2,3,
所以P(X=0)=01-3=,
P(X=1)=1-2=,
P(X=2)=21-=,
P(X=3)=31-0=,
所以X的分布列为
X 0 1 2 3
P
E(X)=0+1+2+3
