任意角的三角函数(湖北省孝感市孝昌县)
文档属性
| 名称 | 任意角的三角函数(湖北省孝感市孝昌县) |

|
|
| 格式 | rar | ||
| 文件大小 | 372.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-11-21 00:00:00 | ||
图片预览




文档简介
课件13张PPT。本课件播放说明:本课件中的动画用VBa制作,动画效果好,图形优美,播放前必修改如下设置:
1、单击“工具”——“选项”——“视图”——取消“以黑幻灯片结束”。
2、单击“工具”——“宏”——“安全性”——选择“低”——“确定”——关闭本课件(powerpoint程序)——重新打开本课件;
3 、如果还不能正常播放本课件,请你重新完全安装office2003以上正版软件。作者:湖北省云梦县曲阳高中宋建祖
邮箱:xgnymsjz@163,com三角函数复习(1)一、内容结构主方图任意角的三角函数和差倍半公式三角函数的图象和性质已知三角函数值求角 本讲重点复习
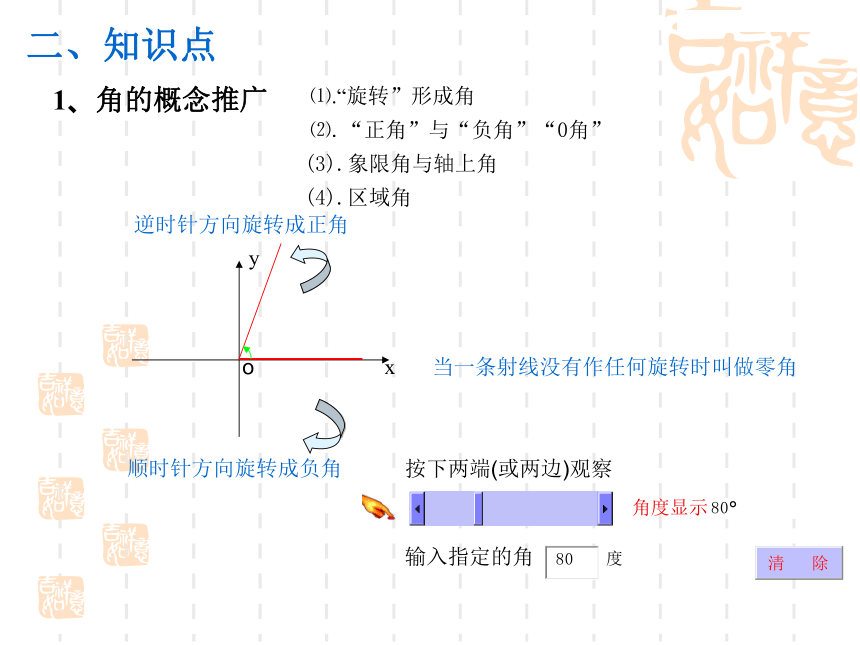
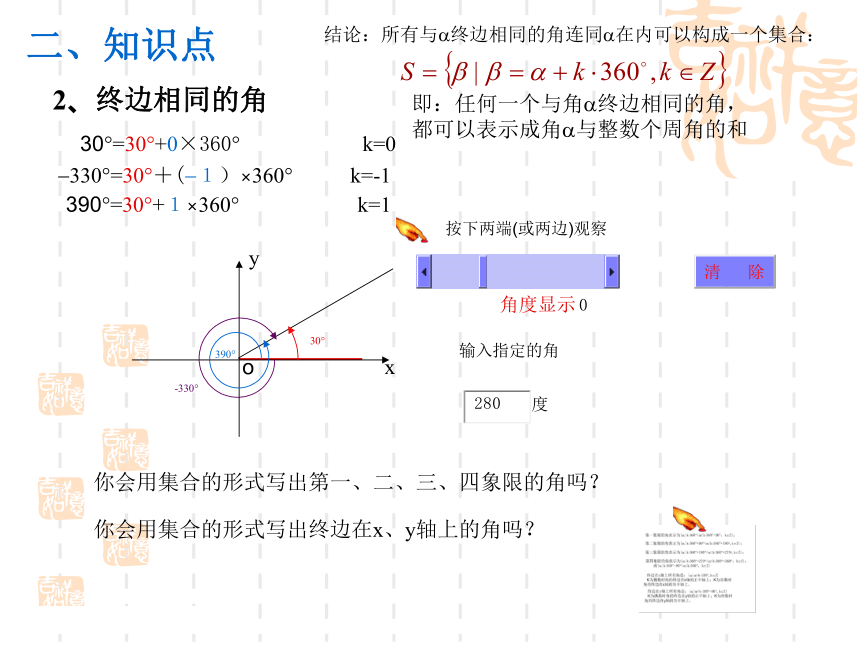
任意角的三角函数1、角的概念推广2、终边相同的角3、弧度制4、任意角的三角函数的定义5、三角函数线角度显示二、知识点1、角的概念推广oxy⑴.“旋转”形成角⑵.“正角”与“负角”“0角”逆时针方向旋转成正角当一条射线没有作任何旋转时叫做零角按下两端(或两边)观察输入指定的角顺时针方向旋转成负角(3).象限角与轴上角(4).区域角角度显示二、知识点2、终边相同的角oxy按下两端(或两边)观察输入指定的角390?
-330?
30?
结论:所有与?终边相同的角连同?在内可以构成一个集合:即:任何一个与角?终边相同的角,
都可以表示成角?与整数个周角的和 ?330?=30?+(?1)×360? k=-1 30?=30?+0×360? k=0 390?=30?+1×360? k=1 你会用集合的形式写出第一、二、三、四象限的角吗?你会用集合的形式写出终边在x、y轴上的角吗?二、知识点3、弧度制定义:长度等于半径长的弧所对的圆心角
称为1弧度的角角度制与弧度制的换算:360?=2?
180?=?2? =360? ?= 180?弧长公式: l=|α| R扇形面积公式 : 你还记得特殊角的转换吗?二、知识点4、任意角的三角函数的定义你记住了它们的定义域吗?P(x,y)为角终上任一点,PO=ro特殊角的三角函数值你记清楚了吗?5、三角函数线正弦值显示角度余弦值正切值二、知识点三角函数线可以帮你记忆:1、象限符号2、函数值的变化3、单调(主)区间按下两端(或两边)观察1.已知α∈[0,2π),命题P:点P(sinα-cosα,tanα)在第一象限.命题q:α∈[π/2,π].则命题P是命题┒q的( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分又不必要条件AA3.在(0,2π)内,使sinα·cosα<0,sinα+cosα>0,同时成立的α的取值范围是( )
(A)(π/2,3π/4 (B)(3π/4,π)
(C)(π/2,3π/4)∪(7π/4,2π) (D)(3π/4,π)∪(3π/2,7π/4) C三、热身练习5、函数的值域是 .{-2,0,2}例1.已知一扇形的中心角是α,所在圆的半径是R.
①若α=60°,R=10cm,求扇形的弧长及该弧所在的弓形面积.
②若扇形的周长是一定值l(l>0),当α为多少弧度时,该扇形的面积有最大值?并求出这一最大值? 【解题回顾】
1、扇形的弧长和面积计算公式都有角度制和弧度制两种给出的方式,但其中用弧度制给出的形式不仅易记,而且好用.在使用时,先要将问题中涉及到的角度换算为弧度. ?
2、解答实际应用题的关键是建模,有关最优问题往往归结为求函数的最值,恰当选择自变量,其定义域源于问题中各量的实际意义,此题②中以半径R为自变量较好,其定义域由弧长大于0而小于周长确定.四、典型例题分析四、典型例题分析【解题回顾】 作出满足条件角的区堿,公共部分为所求.yxo四、典型例题分析【解题回顾】 充要条件的证明必需证条件的两面性,即必要性和充分性.四、典型例题分析【解题回顾】根据三角函数的定义求出r,注意x 的符号计论求解.五、小结
本节课我们复习了任意角三角函数的定义,任意角的三角函数,实质上
是锐角三角函数的扩展,是将锐角三角函数中边的比变为坐标与距离、坐
标与坐标、距离与坐标的比,记忆方法可用锐角三角函数类比记忆,至于
三角函数的定义域可由三角函数的定义分析得到.角的概念推广后,要掌握
象限角、区间角、区域角、终边相同的角等几种角的概念和它们的区别.
角的单位要习惯弧度制,并熟练运用扇形的弧长公式和面积公式。
1、单击“工具”——“选项”——“视图”——取消“以黑幻灯片结束”。
2、单击“工具”——“宏”——“安全性”——选择“低”——“确定”——关闭本课件(powerpoint程序)——重新打开本课件;
3 、如果还不能正常播放本课件,请你重新完全安装office2003以上正版软件。作者:湖北省云梦县曲阳高中宋建祖
邮箱:xgnymsjz@163,com三角函数复习(1)一、内容结构主方图任意角的三角函数和差倍半公式三角函数的图象和性质已知三角函数值求角 本讲重点复习
任意角的三角函数1、角的概念推广2、终边相同的角3、弧度制4、任意角的三角函数的定义5、三角函数线角度显示二、知识点1、角的概念推广oxy⑴.“旋转”形成角⑵.“正角”与“负角”“0角”逆时针方向旋转成正角当一条射线没有作任何旋转时叫做零角按下两端(或两边)观察输入指定的角顺时针方向旋转成负角(3).象限角与轴上角(4).区域角角度显示二、知识点2、终边相同的角oxy按下两端(或两边)观察输入指定的角390?
-330?
30?
结论:所有与?终边相同的角连同?在内可以构成一个集合:即:任何一个与角?终边相同的角,
都可以表示成角?与整数个周角的和 ?330?=30?+(?1)×360? k=-1 30?=30?+0×360? k=0 390?=30?+1×360? k=1 你会用集合的形式写出第一、二、三、四象限的角吗?你会用集合的形式写出终边在x、y轴上的角吗?二、知识点3、弧度制定义:长度等于半径长的弧所对的圆心角
称为1弧度的角角度制与弧度制的换算:360?=2?
180?=?2? =360? ?= 180?弧长公式: l=|α| R扇形面积公式 : 你还记得特殊角的转换吗?二、知识点4、任意角的三角函数的定义你记住了它们的定义域吗?P(x,y)为角终上任一点,PO=ro特殊角的三角函数值你记清楚了吗?5、三角函数线正弦值显示角度余弦值正切值二、知识点三角函数线可以帮你记忆:1、象限符号2、函数值的变化3、单调(主)区间按下两端(或两边)观察1.已知α∈[0,2π),命题P:点P(sinα-cosα,tanα)在第一象限.命题q:α∈[π/2,π].则命题P是命题┒q的( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分又不必要条件AA3.在(0,2π)内,使sinα·cosα<0,sinα+cosα>0,同时成立的α的取值范围是( )
(A)(π/2,3π/4 (B)(3π/4,π)
(C)(π/2,3π/4)∪(7π/4,2π) (D)(3π/4,π)∪(3π/2,7π/4) C三、热身练习5、函数的值域是 .{-2,0,2}例1.已知一扇形的中心角是α,所在圆的半径是R.
①若α=60°,R=10cm,求扇形的弧长及该弧所在的弓形面积.
②若扇形的周长是一定值l(l>0),当α为多少弧度时,该扇形的面积有最大值?并求出这一最大值? 【解题回顾】
1、扇形的弧长和面积计算公式都有角度制和弧度制两种给出的方式,但其中用弧度制给出的形式不仅易记,而且好用.在使用时,先要将问题中涉及到的角度换算为弧度. ?
2、解答实际应用题的关键是建模,有关最优问题往往归结为求函数的最值,恰当选择自变量,其定义域源于问题中各量的实际意义,此题②中以半径R为自变量较好,其定义域由弧长大于0而小于周长确定.四、典型例题分析四、典型例题分析【解题回顾】 作出满足条件角的区堿,公共部分为所求.yxo四、典型例题分析【解题回顾】 充要条件的证明必需证条件的两面性,即必要性和充分性.四、典型例题分析【解题回顾】根据三角函数的定义求出r,注意x 的符号计论求解.五、小结
本节课我们复习了任意角三角函数的定义,任意角的三角函数,实质上
是锐角三角函数的扩展,是将锐角三角函数中边的比变为坐标与距离、坐
标与坐标、距离与坐标的比,记忆方法可用锐角三角函数类比记忆,至于
三角函数的定义域可由三角函数的定义分析得到.角的概念推广后,要掌握
象限角、区间角、区域角、终边相同的角等几种角的概念和它们的区别.
角的单位要习惯弧度制,并熟练运用扇形的弧长公式和面积公式。
