4.2.1由立体图形到试图跟踪训练(含详细解析)
文档属性
| 名称 | 4.2.1由立体图形到试图跟踪训练(含详细解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 284.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-24 00:00:00 | ||
图片预览

文档简介
第四章图形的初步认识4.2.1由立体图形到试图
一.选择题(共8小题)
1.下面的几何体中,主视图为三角形的是( )
A. B. C. D.
2.下列几何体中,同一个几何体的主视图与俯视图不同的是( )
A. 圆柱 B. 正方体 C. 圆锥 D. 球
3.如图是由四个相同的小正方体组成的立体图形,它的俯视图为( )
A. B. C. D.
4.形状相同、大小相等的两个小木块放置于桌面,其俯视图如下图所示,则其主视图是( )
A. B. C. D.
5.如图所示物体的俯视图是( )
A. B. C. D.
6.将两个长方体如图放置,则所构成的几何体的左视图可能是( )
A. B. C D.
7.如图所示的几何体的主视图是( )
A. B. C. D.
8.如图,几何体是由一些正方体组合而成的立体图形,则这个几何体的左视图是( )
A. B. C. D.
二.填空题(共6小题)
9.如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是 _________ .
10.如图是五个相同的正方体堆成的几何体,则它的俯视图是 _________ (填序号①,②等)
11.请写出一个主视图、俯视图有可能完全一样的几何体 _________ .
12.如图,下列水平放置的几何体中,俯视图是正方形的有 _________ 个.
13.如图放置的一个直角三角形ABC(∠C=90°)绕斜边AB旋转一周,所得到的几何体的主视图是下列四个图形中的 _________ (只填序号)
14.如图,是由小立方块搭成几何体的俯视图,上面的数字表示,该位置小立方块的个数画出主视图: _________ ,左视图: _________ .
三.解答题(共8小题)
15.画如图所示几何体的三视图
(1)主视图
(2)左视图
(3)俯视图.
16.5个棱长为1的正方体组成如图的几何体.
(1)该几何体的体积是 _________ (立方单位),表面积是 _________ (平方单位)
(2)画出该几何体的主视图和左视图.
17.学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
碟子的个数 碟子的高度(单位:cm)
1 2
2 2+1.5
3 2+3
4 2+4.5
… …
(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
18.用小立方体搭成一个几何体,使得它的正视图和左视图如图所示,这样的几何体只有一种吗?最少需要多少个小立方块?最多需要多少个小立方块?
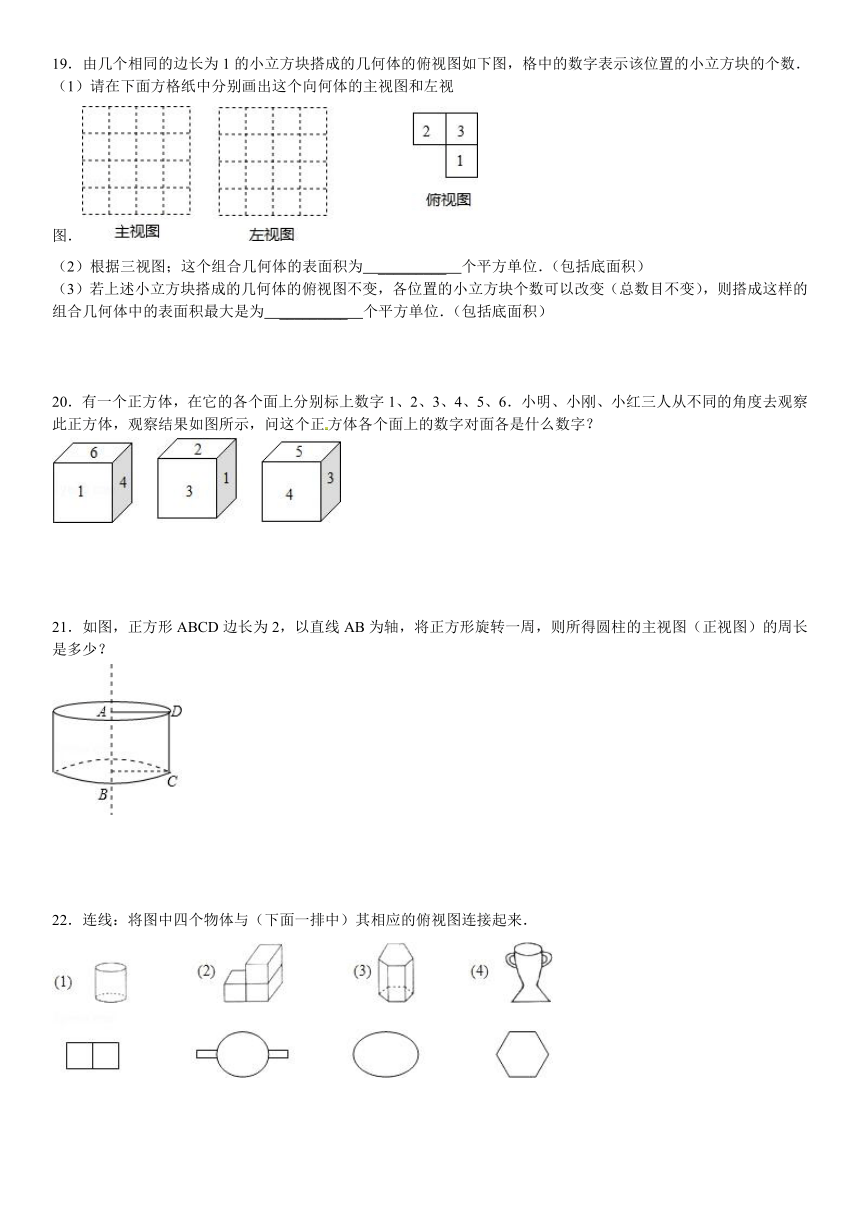
19.由几个相同的边长为1的小立方块搭成的几何体的俯视图如下图,格中的数字表示该位置的小立方块的个数.
(1)请在下面方格纸中分别画出这个向何体的主视图和左视图.
(2)根据三视图;这个组合几何体的表面积为 _________ 个平方单位.(包括底面积)
(3)若上述小立方块搭成的几何体的俯视图不变,各位置的小立方块个数可以改变(总数目不变),则搭成这样的组合几何体中的表面积最大是为 _________ 个平方单位.(包括底面积)
20.有一个正方体,在它的各个面上分别标上数字1、2、3、4、5、6.小明、小刚、小红三人从不同的角度去观察此正方体,观察结果如图所示,问这个正方体各个面上的数字对面各是什么数字?
21.如图,正方形ABCD边长为2,以直线AB为轴,将正方形旋转一周,则所得圆柱的主视图(正视图)的周长是多少?
22.连线:将图中四个物体与(下面一排中)其相应的俯视图连接起来.
第四章图形的初步认识4.2.1由立体图形到试图
参考答案与试题解析
一.选择题(共8小题)
1.下面的几何体中,主视图为三角形的是( )
A. B. C. D.
考点: 简单几何体的三视图.
专题: 常规题型.
分析: 主视图是从几何体的正面看所得到的图形,根据主视图所看的方向,写出每个图形的主视图及可选出答案.
解答: 解:A、主视图是长方形,故A选项错误;
B、主视图是长方形,故B选项错误;
C、主视图是三角形,故C选项正确;
D、主视图是正方形,中间还有一条线,故D选项错误;
故选:C.
点评: 此题主要考查了简单几何体的三视图,关键是掌握主视图所看的位置.
2.下列几何体中,同一个几何体的主视图与俯视图不同的是( )
A. 圆柱 B. 正方体 C. 圆锥 D. 球
考点: 简单几何体的三视图.
分析: 根据主视图是物体从前往后看得到的视图,俯视图是物体从上往下看得到的视图,逐一判断即可.
解答: 解:A、圆柱的主视图是矩形,俯视图是矩形,主视图与俯视图相同,故A选项错误;
B、正方体的主视图是正方形,俯视图是正方形,主视图与俯视图相同,故B选项错误;
C、圆锥的主视图是三角形,俯视图是圆及圆心,主视图与俯视图不相同,故C选项正确;
D、球的主视图是圆,俯视图是圆,主视图与俯视图相同,故D选项错误.
故选:C.
点评: 本题考查了简单几何体的三视图及空间想象能力,比较简单.
3.如图是由四个相同的小正方体组成的立体图形,它的俯视图为( )
A. B. C. D.
考点: 简单组合体的三视图.
分析: 俯视图是从物体上面看所得到的图形.
解答: 解:上面看,是上面2个正方形,左下角1个正方形,
故选:C.
点评: 本题考查了三视图的知识,俯视图是从物体上面看所得到的图形,解答时学生易将三种视图混淆而错误地选其它选项.
4形状相同、大小相等的两个小木块放置于桌面,其俯视图如下图所示,则其主视图是( )
A. B. C. D.
考点: 简单组合体的三视图.
专题: 图表型.
分析: 由实物结合它的俯视图,还原它的具体形状和位置,再判断主视图.
解答: 解:由实物结合它的俯视图可得该物体是由两个长方体木块一个横放一个竖放组合而成,
由此得到它的主视图应为选项D.
故选:D.
点评: 本题考查了物体的三视图.在解题时要注意,看不见的线画成虚线.
5.如图所示物体的俯视图是( )
A. B. C. D.
考点: 简单组合体的三视图.
专题: 常规题型.
分析: 找到从上面看所得到的图形即可,注意所有的看到的棱都应表现在俯视图中.
解答: 解:从上面向下看,易得到横排有3个正方形.
故选:D.
点评: 本题考查了三视图的知识,俯视图是从物体的上面向下看得到的视图.
6.将两个长方体如图放置,则所构成的几何体的左视图可能是( )
A. B. C. D.
考点: 简单组合体的三视图.
分析: 根据从左边看得到的图形是左视图,可得答案.
解答: 解:从左边看,下面是一个矩形,上面是一个等宽的矩形,该矩形的中间有一条棱,
故选:C.
点评: 本题考查了简单组合体的三视图,注意能看到的棱用实线画出.
7.如图所示的几何体的主视图是( )
A. B. C. D.
考点: 简单组合体的三视图.
专题: 常规题型.
分析: 找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.
解答: 解:几何体的主视图是两个长方形,其中一个在另一的上面的左侧,
故选:A.
点评: 本题考查了三视图的知识,主视图是从物体的正面看得到的视图.
8.如图,几何体是由一些正方体组合而成的立体图形,则这个几何体的左视图是( )
A. B. C. D.
考点: 简单组合体的三视图.
专题: 常规题型.
分析: 根据从左边看得到的图形是左视图,可得答案.
解答: 解:从左边看第一层是两个正方形,第二层是左边一个正方形,
故选:D.
点评: 本题考查简单组合体的三视图,从左边看得到的图形是左视图.
二.填空题(共6小题)
9.如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是 左视图 .
考点: 简单组合体的三视图.
专题: 几何图形问题.
分析: 如图可知该几何体的正视图由5个小正方形组成,左视图是由3个小正方形组成,俯视图是由5个小正方形组成,易得解.
解答: 解:如图,该几何体正视图是由5个小正方形组成,
左视图是由3个小正方形组成,
俯视图是由5个小正方形组成,
故三种视图面积最小的是左视图.
故答案为:左视图.
点评: 本题考查的是三视图的知识以及学生对该知识点的巩固,难度属简单.解题关键是找到三种视图的正方形的个数.
10.如图是五个相同的正方体堆成的几何体,则它的俯视图是 ① (填序号①,②等)
考点: 简单组合体的三视图.
分析: 根据俯视图是从上面看到的图象判定则可.
解答: 解:从上面看几何体的左边是三个正方体,右边是一个正方体.故答案是①.
点评: 本题考查了三种视图中的俯视图,比较简单.
11.请写出一个主视图、俯视图有可能完全一样的几何体 球或正方体 .
考点: 简单几何体的三视图.
专题: 开放型.
分析: 主视图、俯视图是分别从物体正面和上面看,所得到的图形.
解答: 解:球的三视图都为圆,所以主视图、俯视图完全一样;
正方体的三视图为正方形,所以主视图、俯视图完全一样;
故答案为球或正方体.
点评: 考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.
12.如图,下列水平放置的几何体中,俯视图是正方形的有 1 个.
考点: 简单几何体的三视图.
专题: 几何图形问题.
分析: 可根据各几何体的特点,得出俯视图形状是正方形即可.
解答: 解:正方体的俯视图为正方形,符合题意;
该长方的俯视图是矩形,不符合题意;
圆柱的俯视图是圆形,不符合题意;
三棱柱的俯视图是三角形,不符合题意.
故答案为:1.
点评: 此题主要考查了几何体的三种视图,掌握定义是关键.俯视图是从物体上面看,所得到的图形.
13.如图放置的一个直角三角形ABC(∠C=90°)绕斜边AB旋转一周,所得到的几何体的主视图是下列四个图形中的 ② (只填序号)
考点: 简单几何体的三视图.
专题: 压轴题.
分析: 充分发挥空间想象能力,旋转一周所得的几何体是两个底面相等相连的圆锥,圆锥的左视图是等腰三角形,所以该几何体的左视图是两个底边相等的等腰三角形相连.
解答: 解:根据分析,可得图②
故答案为:②.
点评: 本题考查了空间想象能力及几何体的三视图.
14.如图,是由小立方块搭成几何体的俯视图,上面的数字表示,该位置小立方块的个数画出主视图: ,左视图: .
考点: 作图-三视图;由三视图判断几何体.
分析: 由已知条件可知,主视图有3列,每列小正方数形数目分别为3,2,3;左视图有2列,每列小正方形数目分别为3,2.据此可画出图形.
解答: 解:如图所示:
点评: 本题考查几何体的三视图画法.由几何体的俯视图及小正方形内的数字,可知主视图的列数与俯视数的列数相同,且每列小正方形数目为俯视图中该列小正方形数字中的最大数字.左视图的列数与俯视图的行数相同,且每列小正方形数目为俯视图中相应行中正方形数字中的最大数字.
三.解答题(共8小题)
15.画如图所示几何体的三视图
(1)主视图
(2)左视图
(3)俯视图.
考点: 作图-三视图.
分析: (1)根据实际物体,主视图有两列分别不同形状的长方形;
(2)左视图为两个长方形拼接而成;
(3)俯视图为一大长方形和一小长方形拼接而成.
解答: 解:(1)主视图如图所示:
(2)左视图如图所示:
(3)俯视图如图所示:
点评: 此题主要考查了如何画三视图,具体画法及步骤:①确定主视图位置,画出主视图;②在主视图的正下方画出俯视图,注意与主视图“长对正”;③在主视图的正右方画出左视图,注意与主视图“高平齐”、与俯视图“宽相等”.
16.5个棱长为1的正方体组成如图的几何体.
(1)该几何体的体积是 5 (立方单位),表面积是 22 (平方单位)
(2)画出该几何体的主视图和左视图.
考点: 作图-三视图.
专题: 作图题.
分析: (1)几何体的体积为5个正方体的体积和,表面积为22个正方形的面积;
(2)主视图从左往右看3列正方形的个数依次为2,1,2;左视图1列正方形的个数为2.
解答: 解:(1)每个正方体的体积为1,∴组合几何体的体积为5×1=5;
∵组合几何体的前面和后面共有5×2=10个正方形,上下共有6个正方形,左右共6个正方形,每个正方形的面积为1,
∴组合几何体的表面积为22.
故答案为:5,22;
(2)作图如下:
点评: 考查组合几何体的计算和三视图的画法;用到的知识点为:主视图,左视图分别是从物体的正面和左面看到的平面图形.
17.学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
碟子的个数 碟子的高度(单位:cm)
1 2
2 2+1.5
3 2+3
4 2+4.5
… …
(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
考点: 简单组合体的三视图;代数式求值.
专题: 图表型.
分析: 由表中给出的碟子个数与碟子高度的规律,可以看出碟子数为x时,碟子的高度为2+1.5(x﹣1).
解答: 解:由题意得:
(1)2+1.5(x﹣1)=1.5x+0.5
(2)由三视图可知共有12个碟子
∴叠成一摞的高度=1.5×12+0.5=18.5(cm)
点评: 考查获取信息(读表)、分析问题解决问题的能力.
找出碟子个数与碟子高度的之间的关系式是此题的关键.
18.用小立方体搭成一个几何体,使得它的正视图和左视图如图所示,这样的几何体只有一种吗?最少需要多少个小立方块?最多需要多少个小立方块?
考点: 简单组合体的三视图.
分析: 这种题需要空间想象能力,可以想象这样的小立方体搭了上中下三层,但只有从左到右的二排,符合题中两个视图的几何体不只一种.
解答: 解:最少需要6块如图(1),最多需要9块如图(2)
点评: 本题灵活考查了三种视图之间的关系以及视图和实物之间的关系,同时还考查了对图形的想象力.
19.由几个相同的边长为1的小立方块搭成的几何体的俯视图如下图,格中的数字表示该位置的小立方块的个数.
(1)请在下面方格纸中分别画出这个向何体的主视图和左视图.
(2)根据三视图;这个组合几何体的表面积为 24 个平方单位.(包括底面积)
(3)若上述小立方块搭成的几何体的俯视图不变,各位置的小立方块个数可以改变(总数目不变),则搭成这样的组合几何体中的表面积最大是为 26 个平方单位.(包括底面积)
考点: 简单组合体的三视图;几何体的表面积.
专题: 计算题.
分析: (1)主视图有2列,每列小正方形数目分别为2,3;左视图有2列,每列小正方形数目分别为3,1;
(2)上面共有3个小正方形,下面共有3个小正方形;左面共有4个小正方形,右面共有4个正方形;前面共有5个小正方形,后面共有5个正方形,继而可得出表面积.
(3)要使表面积最大,则需满足两正方体重合的最少,画出俯视图,计算表面积即可.
解答: 解:(1)主视图有2列,每列小正方形数目分别为2,3;左视图有2列,每列小正方形数目分别为3,1,
图形分别如下:
(2)由题意可得:上面共有3个小正方形,下面共有3个小正方形;左面共有4个小正方形,右面共有4个正方形;前面共有5个小正方形,后面共有5个正方形,
故可得表面积为:1×(3+3+4+4+5+5)=24.
(3)要使表面积最大,则需满足两正方体重合的最少,此时俯视图为:
这样上面共有3个小正方形,下面共有3个小正方形;左面共有5个小正方形,右面共有5个正方形;前面共有5个小正方形,后面共有5个正方形,
表面积为:1×(3+3+5+5+5+5)=26.
故答案为:24、26.
点评: 此题考查了简单几何体的三视图及几何体的表面积的计算,解答本题的关键是掌握三视图的观察方法,在计算表面积时容易出错,要一个面一个面的进行查找,避免遗漏,有一定难度.
20.有一个正方体,在它的各个面上分别标上数字1、2、3、4、5、6.小明、小刚、小红三人从不同的角度去观察此正方体,观察结果如图所示,问这个正方体各个面上的数字对面各是什么数字?
考点: 简单几何体的三视图.
分析: 由图一和图二可看出看出1的相对面是5;再由图二和图三可看出看出3的相对面是6,从而2的相对面是4.
解答: 解:从3个小立方体上的数可知,
与写有数字1的面相邻的面上数字是2,3,4,6,
所以数字1面对数字5面,
同理,立方体面上数字3对6.
故立方体面上数字2对4.
点评: 本题考查灵活运用正方体的相对面解答问题,立意新颖,是一道不错的题.解题的关键是按照相邻和所给图形得到其他.
21.如图,正方形ABCD边长为2,以直线AB为轴,将正方形旋转一周,则所得圆柱的主视图(正视图)的周长是多少?
考点: 简单几何体的三视图;点、线、面、体.
分析: 判断出圆柱的主视图矩形的长和宽,再根据矩形的周长公式列式计算即可得解.
解答: 解:由题意得,所得圆柱的主视图是长为4,宽为2的矩形,
周长=2×(2+4)=12.
点评: 本题考查了几何体的三种视图,判断出主视图的形状与长和宽是解题的关键.
22.连线:将图中四个物体与(下面一排中)其相应的俯视图连接起来.
考点: 简单组合体的三视图.
分析: 俯视图是从物体上面所看到的图形,可根据各立体图形的特点进行判断.
解答: 解:如图所示:
点评: 考查学生对俯视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.
一.选择题(共8小题)
1.下面的几何体中,主视图为三角形的是( )
A. B. C. D.
2.下列几何体中,同一个几何体的主视图与俯视图不同的是( )
A. 圆柱 B. 正方体 C. 圆锥 D. 球
3.如图是由四个相同的小正方体组成的立体图形,它的俯视图为( )
A. B. C. D.
4.形状相同、大小相等的两个小木块放置于桌面,其俯视图如下图所示,则其主视图是( )
A. B. C. D.
5.如图所示物体的俯视图是( )
A. B. C. D.
6.将两个长方体如图放置,则所构成的几何体的左视图可能是( )
A. B. C D.
7.如图所示的几何体的主视图是( )
A. B. C. D.
8.如图,几何体是由一些正方体组合而成的立体图形,则这个几何体的左视图是( )
A. B. C. D.
二.填空题(共6小题)
9.如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是 _________ .
10.如图是五个相同的正方体堆成的几何体,则它的俯视图是 _________ (填序号①,②等)
11.请写出一个主视图、俯视图有可能完全一样的几何体 _________ .
12.如图,下列水平放置的几何体中,俯视图是正方形的有 _________ 个.
13.如图放置的一个直角三角形ABC(∠C=90°)绕斜边AB旋转一周,所得到的几何体的主视图是下列四个图形中的 _________ (只填序号)
14.如图,是由小立方块搭成几何体的俯视图,上面的数字表示,该位置小立方块的个数画出主视图: _________ ,左视图: _________ .
三.解答题(共8小题)
15.画如图所示几何体的三视图
(1)主视图
(2)左视图
(3)俯视图.
16.5个棱长为1的正方体组成如图的几何体.
(1)该几何体的体积是 _________ (立方单位),表面积是 _________ (平方单位)
(2)画出该几何体的主视图和左视图.
17.学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
碟子的个数 碟子的高度(单位:cm)
1 2
2 2+1.5
3 2+3
4 2+4.5
… …
(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
18.用小立方体搭成一个几何体,使得它的正视图和左视图如图所示,这样的几何体只有一种吗?最少需要多少个小立方块?最多需要多少个小立方块?
19.由几个相同的边长为1的小立方块搭成的几何体的俯视图如下图,格中的数字表示该位置的小立方块的个数.
(1)请在下面方格纸中分别画出这个向何体的主视图和左视图.
(2)根据三视图;这个组合几何体的表面积为 _________ 个平方单位.(包括底面积)
(3)若上述小立方块搭成的几何体的俯视图不变,各位置的小立方块个数可以改变(总数目不变),则搭成这样的组合几何体中的表面积最大是为 _________ 个平方单位.(包括底面积)
20.有一个正方体,在它的各个面上分别标上数字1、2、3、4、5、6.小明、小刚、小红三人从不同的角度去观察此正方体,观察结果如图所示,问这个正方体各个面上的数字对面各是什么数字?
21.如图,正方形ABCD边长为2,以直线AB为轴,将正方形旋转一周,则所得圆柱的主视图(正视图)的周长是多少?
22.连线:将图中四个物体与(下面一排中)其相应的俯视图连接起来.
第四章图形的初步认识4.2.1由立体图形到试图
参考答案与试题解析
一.选择题(共8小题)
1.下面的几何体中,主视图为三角形的是( )
A. B. C. D.
考点: 简单几何体的三视图.
专题: 常规题型.
分析: 主视图是从几何体的正面看所得到的图形,根据主视图所看的方向,写出每个图形的主视图及可选出答案.
解答: 解:A、主视图是长方形,故A选项错误;
B、主视图是长方形,故B选项错误;
C、主视图是三角形,故C选项正确;
D、主视图是正方形,中间还有一条线,故D选项错误;
故选:C.
点评: 此题主要考查了简单几何体的三视图,关键是掌握主视图所看的位置.
2.下列几何体中,同一个几何体的主视图与俯视图不同的是( )
A. 圆柱 B. 正方体 C. 圆锥 D. 球
考点: 简单几何体的三视图.
分析: 根据主视图是物体从前往后看得到的视图,俯视图是物体从上往下看得到的视图,逐一判断即可.
解答: 解:A、圆柱的主视图是矩形,俯视图是矩形,主视图与俯视图相同,故A选项错误;
B、正方体的主视图是正方形,俯视图是正方形,主视图与俯视图相同,故B选项错误;
C、圆锥的主视图是三角形,俯视图是圆及圆心,主视图与俯视图不相同,故C选项正确;
D、球的主视图是圆,俯视图是圆,主视图与俯视图相同,故D选项错误.
故选:C.
点评: 本题考查了简单几何体的三视图及空间想象能力,比较简单.
3.如图是由四个相同的小正方体组成的立体图形,它的俯视图为( )
A. B. C. D.
考点: 简单组合体的三视图.
分析: 俯视图是从物体上面看所得到的图形.
解答: 解:上面看,是上面2个正方形,左下角1个正方形,
故选:C.
点评: 本题考查了三视图的知识,俯视图是从物体上面看所得到的图形,解答时学生易将三种视图混淆而错误地选其它选项.
4形状相同、大小相等的两个小木块放置于桌面,其俯视图如下图所示,则其主视图是( )
A. B. C. D.
考点: 简单组合体的三视图.
专题: 图表型.
分析: 由实物结合它的俯视图,还原它的具体形状和位置,再判断主视图.
解答: 解:由实物结合它的俯视图可得该物体是由两个长方体木块一个横放一个竖放组合而成,
由此得到它的主视图应为选项D.
故选:D.
点评: 本题考查了物体的三视图.在解题时要注意,看不见的线画成虚线.
5.如图所示物体的俯视图是( )
A. B. C. D.
考点: 简单组合体的三视图.
专题: 常规题型.
分析: 找到从上面看所得到的图形即可,注意所有的看到的棱都应表现在俯视图中.
解答: 解:从上面向下看,易得到横排有3个正方形.
故选:D.
点评: 本题考查了三视图的知识,俯视图是从物体的上面向下看得到的视图.
6.将两个长方体如图放置,则所构成的几何体的左视图可能是( )
A. B. C. D.
考点: 简单组合体的三视图.
分析: 根据从左边看得到的图形是左视图,可得答案.
解答: 解:从左边看,下面是一个矩形,上面是一个等宽的矩形,该矩形的中间有一条棱,
故选:C.
点评: 本题考查了简单组合体的三视图,注意能看到的棱用实线画出.
7.如图所示的几何体的主视图是( )
A. B. C. D.
考点: 简单组合体的三视图.
专题: 常规题型.
分析: 找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.
解答: 解:几何体的主视图是两个长方形,其中一个在另一的上面的左侧,
故选:A.
点评: 本题考查了三视图的知识,主视图是从物体的正面看得到的视图.
8.如图,几何体是由一些正方体组合而成的立体图形,则这个几何体的左视图是( )
A. B. C. D.
考点: 简单组合体的三视图.
专题: 常规题型.
分析: 根据从左边看得到的图形是左视图,可得答案.
解答: 解:从左边看第一层是两个正方形,第二层是左边一个正方形,
故选:D.
点评: 本题考查简单组合体的三视图,从左边看得到的图形是左视图.
二.填空题(共6小题)
9.如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是 左视图 .
考点: 简单组合体的三视图.
专题: 几何图形问题.
分析: 如图可知该几何体的正视图由5个小正方形组成,左视图是由3个小正方形组成,俯视图是由5个小正方形组成,易得解.
解答: 解:如图,该几何体正视图是由5个小正方形组成,
左视图是由3个小正方形组成,
俯视图是由5个小正方形组成,
故三种视图面积最小的是左视图.
故答案为:左视图.
点评: 本题考查的是三视图的知识以及学生对该知识点的巩固,难度属简单.解题关键是找到三种视图的正方形的个数.
10.如图是五个相同的正方体堆成的几何体,则它的俯视图是 ① (填序号①,②等)
考点: 简单组合体的三视图.
分析: 根据俯视图是从上面看到的图象判定则可.
解答: 解:从上面看几何体的左边是三个正方体,右边是一个正方体.故答案是①.
点评: 本题考查了三种视图中的俯视图,比较简单.
11.请写出一个主视图、俯视图有可能完全一样的几何体 球或正方体 .
考点: 简单几何体的三视图.
专题: 开放型.
分析: 主视图、俯视图是分别从物体正面和上面看,所得到的图形.
解答: 解:球的三视图都为圆,所以主视图、俯视图完全一样;
正方体的三视图为正方形,所以主视图、俯视图完全一样;
故答案为球或正方体.
点评: 考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.
12.如图,下列水平放置的几何体中,俯视图是正方形的有 1 个.
考点: 简单几何体的三视图.
专题: 几何图形问题.
分析: 可根据各几何体的特点,得出俯视图形状是正方形即可.
解答: 解:正方体的俯视图为正方形,符合题意;
该长方的俯视图是矩形,不符合题意;
圆柱的俯视图是圆形,不符合题意;
三棱柱的俯视图是三角形,不符合题意.
故答案为:1.
点评: 此题主要考查了几何体的三种视图,掌握定义是关键.俯视图是从物体上面看,所得到的图形.
13.如图放置的一个直角三角形ABC(∠C=90°)绕斜边AB旋转一周,所得到的几何体的主视图是下列四个图形中的 ② (只填序号)
考点: 简单几何体的三视图.
专题: 压轴题.
分析: 充分发挥空间想象能力,旋转一周所得的几何体是两个底面相等相连的圆锥,圆锥的左视图是等腰三角形,所以该几何体的左视图是两个底边相等的等腰三角形相连.
解答: 解:根据分析,可得图②
故答案为:②.
点评: 本题考查了空间想象能力及几何体的三视图.
14.如图,是由小立方块搭成几何体的俯视图,上面的数字表示,该位置小立方块的个数画出主视图: ,左视图: .
考点: 作图-三视图;由三视图判断几何体.
分析: 由已知条件可知,主视图有3列,每列小正方数形数目分别为3,2,3;左视图有2列,每列小正方形数目分别为3,2.据此可画出图形.
解答: 解:如图所示:
点评: 本题考查几何体的三视图画法.由几何体的俯视图及小正方形内的数字,可知主视图的列数与俯视数的列数相同,且每列小正方形数目为俯视图中该列小正方形数字中的最大数字.左视图的列数与俯视图的行数相同,且每列小正方形数目为俯视图中相应行中正方形数字中的最大数字.
三.解答题(共8小题)
15.画如图所示几何体的三视图
(1)主视图
(2)左视图
(3)俯视图.
考点: 作图-三视图.
分析: (1)根据实际物体,主视图有两列分别不同形状的长方形;
(2)左视图为两个长方形拼接而成;
(3)俯视图为一大长方形和一小长方形拼接而成.
解答: 解:(1)主视图如图所示:
(2)左视图如图所示:
(3)俯视图如图所示:
点评: 此题主要考查了如何画三视图,具体画法及步骤:①确定主视图位置,画出主视图;②在主视图的正下方画出俯视图,注意与主视图“长对正”;③在主视图的正右方画出左视图,注意与主视图“高平齐”、与俯视图“宽相等”.
16.5个棱长为1的正方体组成如图的几何体.
(1)该几何体的体积是 5 (立方单位),表面积是 22 (平方单位)
(2)画出该几何体的主视图和左视图.
考点: 作图-三视图.
专题: 作图题.
分析: (1)几何体的体积为5个正方体的体积和,表面积为22个正方形的面积;
(2)主视图从左往右看3列正方形的个数依次为2,1,2;左视图1列正方形的个数为2.
解答: 解:(1)每个正方体的体积为1,∴组合几何体的体积为5×1=5;
∵组合几何体的前面和后面共有5×2=10个正方形,上下共有6个正方形,左右共6个正方形,每个正方形的面积为1,
∴组合几何体的表面积为22.
故答案为:5,22;
(2)作图如下:
点评: 考查组合几何体的计算和三视图的画法;用到的知识点为:主视图,左视图分别是从物体的正面和左面看到的平面图形.
17.学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
碟子的个数 碟子的高度(单位:cm)
1 2
2 2+1.5
3 2+3
4 2+4.5
… …
(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
考点: 简单组合体的三视图;代数式求值.
专题: 图表型.
分析: 由表中给出的碟子个数与碟子高度的规律,可以看出碟子数为x时,碟子的高度为2+1.5(x﹣1).
解答: 解:由题意得:
(1)2+1.5(x﹣1)=1.5x+0.5
(2)由三视图可知共有12个碟子
∴叠成一摞的高度=1.5×12+0.5=18.5(cm)
点评: 考查获取信息(读表)、分析问题解决问题的能力.
找出碟子个数与碟子高度的之间的关系式是此题的关键.
18.用小立方体搭成一个几何体,使得它的正视图和左视图如图所示,这样的几何体只有一种吗?最少需要多少个小立方块?最多需要多少个小立方块?
考点: 简单组合体的三视图.
分析: 这种题需要空间想象能力,可以想象这样的小立方体搭了上中下三层,但只有从左到右的二排,符合题中两个视图的几何体不只一种.
解答: 解:最少需要6块如图(1),最多需要9块如图(2)
点评: 本题灵活考查了三种视图之间的关系以及视图和实物之间的关系,同时还考查了对图形的想象力.
19.由几个相同的边长为1的小立方块搭成的几何体的俯视图如下图,格中的数字表示该位置的小立方块的个数.
(1)请在下面方格纸中分别画出这个向何体的主视图和左视图.
(2)根据三视图;这个组合几何体的表面积为 24 个平方单位.(包括底面积)
(3)若上述小立方块搭成的几何体的俯视图不变,各位置的小立方块个数可以改变(总数目不变),则搭成这样的组合几何体中的表面积最大是为 26 个平方单位.(包括底面积)
考点: 简单组合体的三视图;几何体的表面积.
专题: 计算题.
分析: (1)主视图有2列,每列小正方形数目分别为2,3;左视图有2列,每列小正方形数目分别为3,1;
(2)上面共有3个小正方形,下面共有3个小正方形;左面共有4个小正方形,右面共有4个正方形;前面共有5个小正方形,后面共有5个正方形,继而可得出表面积.
(3)要使表面积最大,则需满足两正方体重合的最少,画出俯视图,计算表面积即可.
解答: 解:(1)主视图有2列,每列小正方形数目分别为2,3;左视图有2列,每列小正方形数目分别为3,1,
图形分别如下:
(2)由题意可得:上面共有3个小正方形,下面共有3个小正方形;左面共有4个小正方形,右面共有4个正方形;前面共有5个小正方形,后面共有5个正方形,
故可得表面积为:1×(3+3+4+4+5+5)=24.
(3)要使表面积最大,则需满足两正方体重合的最少,此时俯视图为:
这样上面共有3个小正方形,下面共有3个小正方形;左面共有5个小正方形,右面共有5个正方形;前面共有5个小正方形,后面共有5个正方形,
表面积为:1×(3+3+5+5+5+5)=26.
故答案为:24、26.
点评: 此题考查了简单几何体的三视图及几何体的表面积的计算,解答本题的关键是掌握三视图的观察方法,在计算表面积时容易出错,要一个面一个面的进行查找,避免遗漏,有一定难度.
20.有一个正方体,在它的各个面上分别标上数字1、2、3、4、5、6.小明、小刚、小红三人从不同的角度去观察此正方体,观察结果如图所示,问这个正方体各个面上的数字对面各是什么数字?
考点: 简单几何体的三视图.
分析: 由图一和图二可看出看出1的相对面是5;再由图二和图三可看出看出3的相对面是6,从而2的相对面是4.
解答: 解:从3个小立方体上的数可知,
与写有数字1的面相邻的面上数字是2,3,4,6,
所以数字1面对数字5面,
同理,立方体面上数字3对6.
故立方体面上数字2对4.
点评: 本题考查灵活运用正方体的相对面解答问题,立意新颖,是一道不错的题.解题的关键是按照相邻和所给图形得到其他.
21.如图,正方形ABCD边长为2,以直线AB为轴,将正方形旋转一周,则所得圆柱的主视图(正视图)的周长是多少?
考点: 简单几何体的三视图;点、线、面、体.
分析: 判断出圆柱的主视图矩形的长和宽,再根据矩形的周长公式列式计算即可得解.
解答: 解:由题意得,所得圆柱的主视图是长为4,宽为2的矩形,
周长=2×(2+4)=12.
点评: 本题考查了几何体的三种视图,判断出主视图的形状与长和宽是解题的关键.
22.连线:将图中四个物体与(下面一排中)其相应的俯视图连接起来.
考点: 简单组合体的三视图.
分析: 俯视图是从物体上面所看到的图形,可根据各立体图形的特点进行判断.
解答: 解:如图所示:
点评: 考查学生对俯视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
