4.2.2由视图到立体图形跟踪训练(含详细解析)
文档属性
| 名称 | 4.2.2由视图到立体图形跟踪训练(含详细解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 213.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-24 00:00:00 | ||
图片预览

文档简介
第四章图形的初步认识4.2.2由视图到立体图形
一.选择题(共8小题)
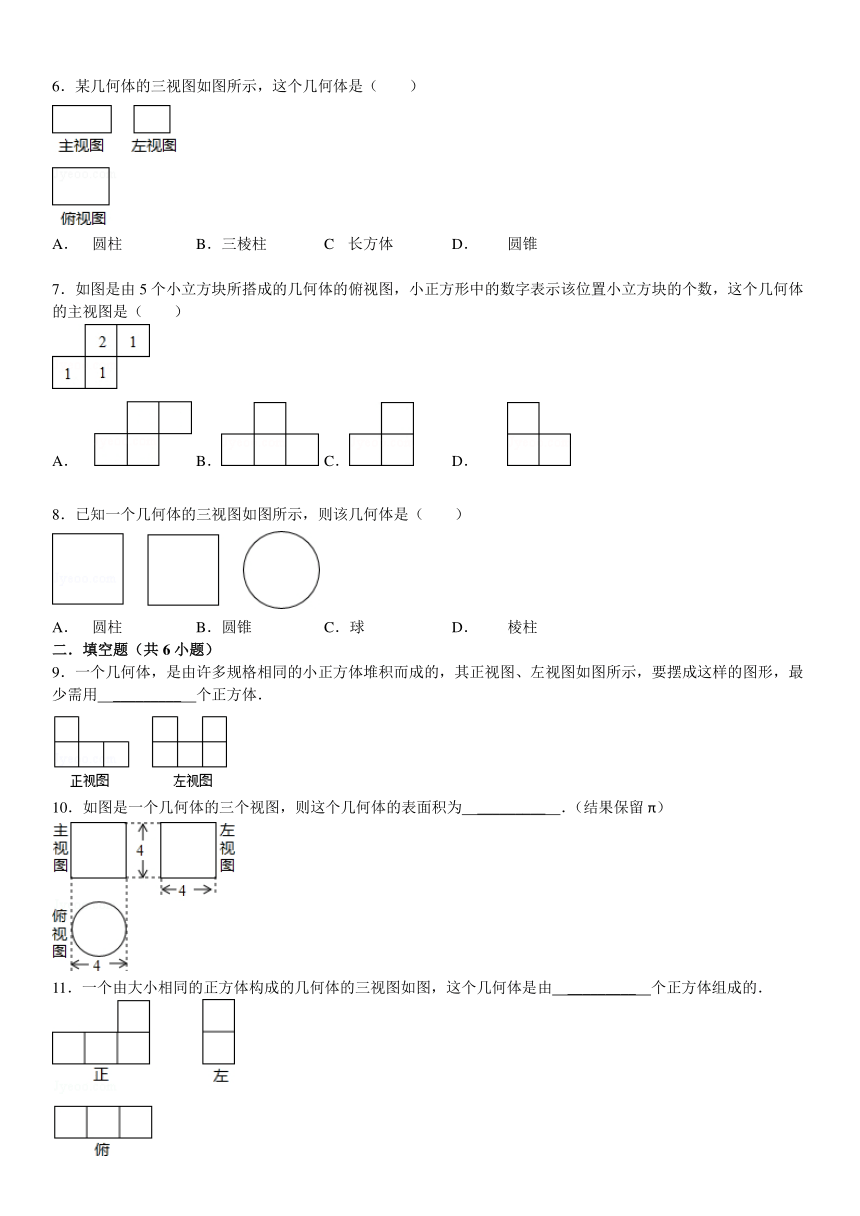
1.如图是由几个相同的小正方体搭成的几何体的三视图,则搭成这个几何体的小正方体的个数是( )
A. 4个 B.5个 C.6个 D. 7个
2.若图是由几个相同的小正方体搭成的几何体的主视图和俯视图,则搭成这个几何体的小正方体的个数最少是( )
A. 6 B.8 C.10 D. 12
3.一个几何体的三视图如图所示,这个几何体是( )
A. 棱柱 B.圆柱 C.圆锥 D. 球
4.某几何体的三视图如图所示,则这个几何体是( )
A. 圆柱 B.正方体 C.球 D. 圆锥
5.如图所示的主视图、左视图、俯视图是下列哪个物体的三视图( )
A. B. C. D.
6.某几何体的三视图如图所示,这个几何体是( )
A. 圆柱 B.三棱柱 C 长方体 D. 圆锥
7.如图是由5个小立方块所搭成的几何体的俯视图,小正方形中的数字表示该位置小立方块的个数,这个几何体的主视图是( )
A. B. C. D.
8.已知一个几何体的三视图如图所示,则该几何体是( )
A. 圆柱 B.圆锥 C.球 D. 棱柱
二.填空题(共6小题)
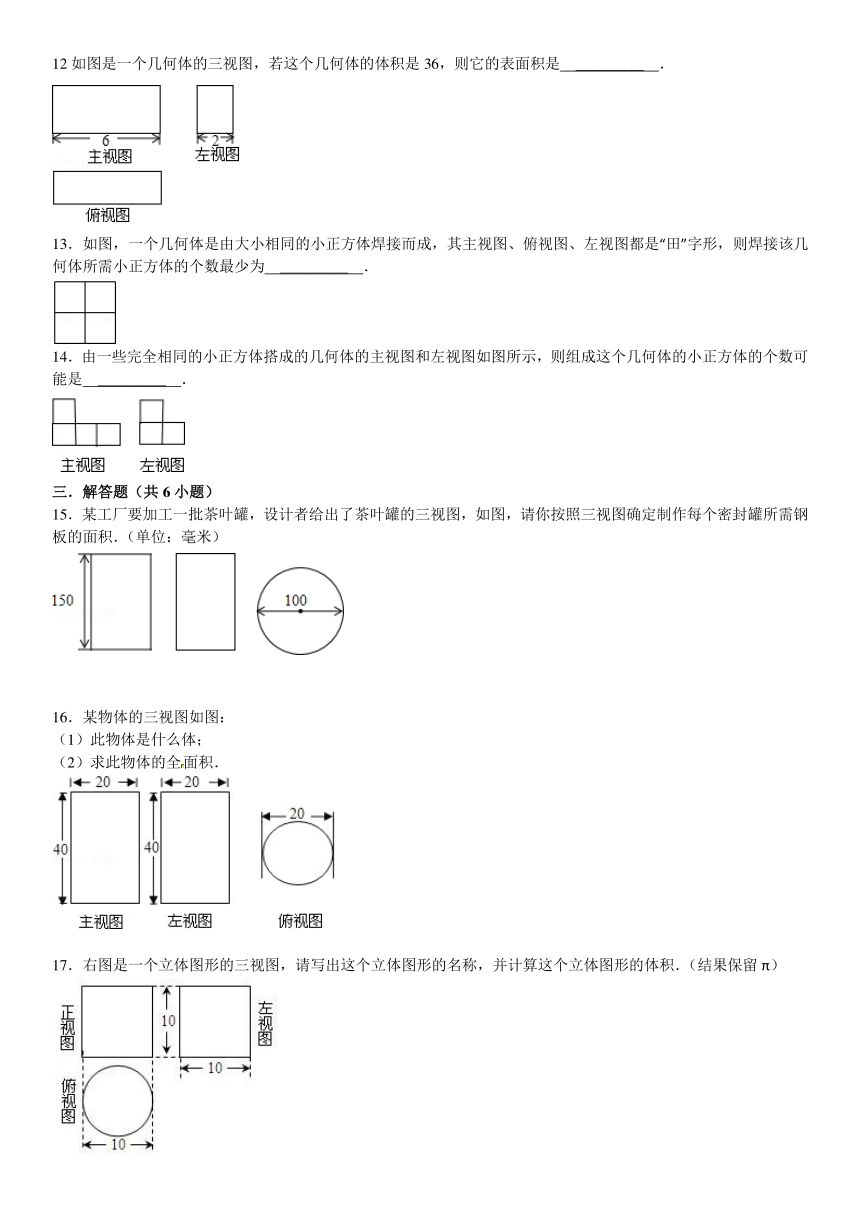
9.一个几何体,是由许多规格相同的小正方体堆积而成的,其正视图、左视图如图所示,要摆成这样的图形,最少需用 _________ 个正方体.
10.如图是一个几何体的三个视图,则这个几何体的表面积为 _________ .(结果保留π)
11.一个由大小相同的正方体构成的几何体的三视图如图,这个几何体是由 _________ 个正方体组成的.
12如图是一个几何体的三视图,若这个几何体的体积是36,则它的表面积是 _________ .
13.如图,一个几何体是由大小相同的小正方体焊接而成,其主视图、俯视图、左视图都是“田”字形,则焊接该几何体所需小正方体的个数最少为 _________ .
14.由一些完全相同的小正方体搭成的几何体的主视图和左视图如图所示,则组成这个几何体的小正方体的个数可能是 _________ .
三.解答题(共6小题)
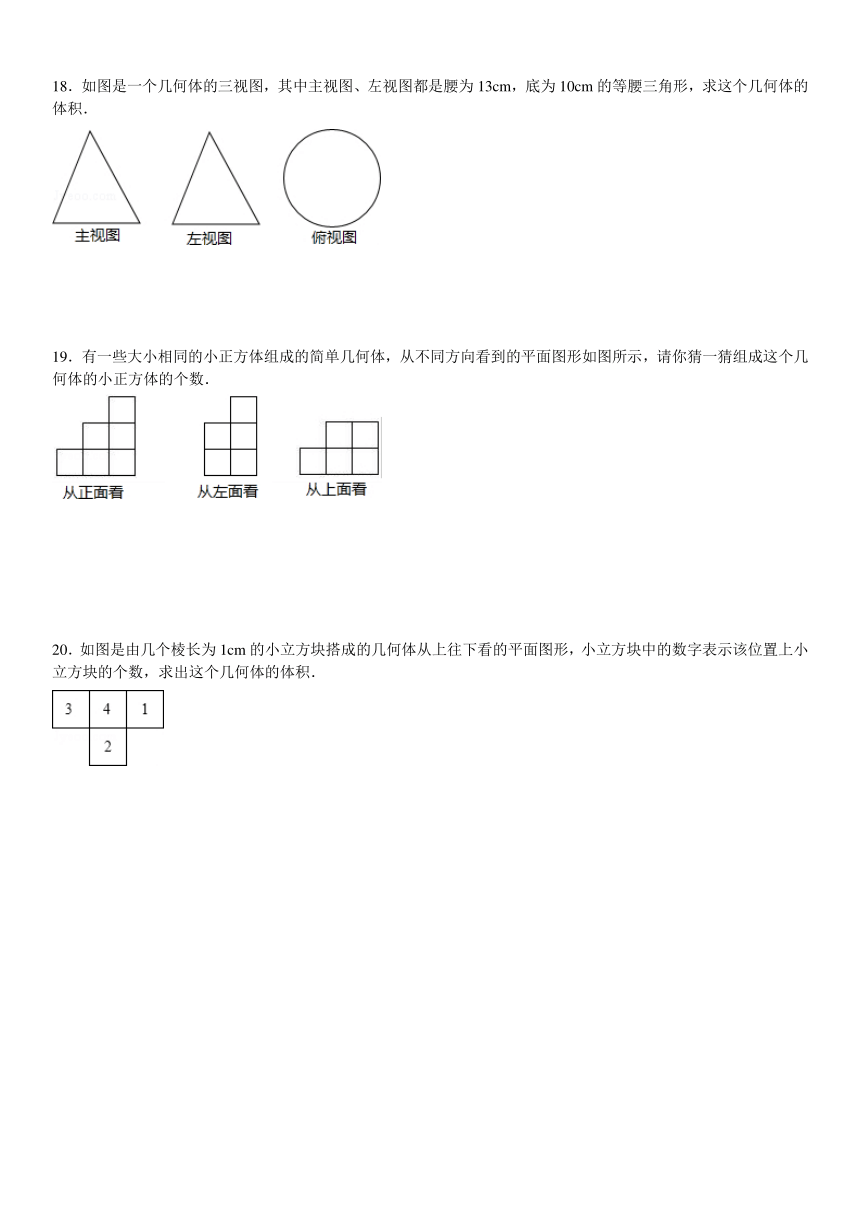
15.某工厂要加工一批茶叶罐,设计者给出了茶叶罐的三视图,如图,请你按照三视图确定制作每个密封罐所需钢板的面积.(单位:毫米)
16.某物体的三视图如图:
(1)此物体是什么体;
(2)求此物体的全面积.
17.右图是一个立体图形的三视图,请写出这个立体图形的名称,并计算这个立体图形的体积.(结果保留π)
18.如图是一个几何体的三视图,其中主视图、左视图都是腰为13cm,底为10cm的等腰三角形,求这个几何体的体积.
19.有一些大小相同的小正方体组成的简单几何体,从不同方向看到的平面图形如图所示,请你猜一猜组成这个几何体的小正方体的个数.
20.如图是由几个棱长为1cm的小立方块搭成的几何体从上往下看的平面图形,小立方块中的数字表示该位置上小立方块的个数,求出这个几何体的体积.
第四章图形的初步认识4.2.2由视图到立体图形
参考答案与试题解析
一.选择题(共8小题)
1.如图是由几个相同的小正方体搭成的几何体的三视图,则搭成这个几何体的小正方体的个数是( )
A. 4个 B.5个 C.6个 D. 7个
考点: 由三视图判断几何体.
分析: 根据给出的几何体,通过动手操作,观察可得答案为4,也可以根据画三视图的方法,发挥空间想象能力,直接想象出每个位置正方体的数目,再加上来.
解答: 解:由三视图可得,需要的小正方体的数目:1+2+1=4.如图:
故选:A.
点评: 本题考查了几何体的三视图及空间想象能力.
2.若图是由几个相同的小正方体搭成的几何体的主视图和俯视图,则搭成这个几何体的小正方体的个数最少是( )
A. 6 B.8 C.10 D. 12
考点: 由三视图判断几何体.
专题: 几何图形问题.
分析: 根据主视图以及俯视图,可得出共有2行,根据俯视图可得出该几何体由2列组成,故可得出小正方体最少块数.
解答: 解:综合主视图和俯视图,底层最少有4个小立方体,第二层最少有2个小立方体,
因此搭成这个几何体的小正方体的个数最少是6个.
故选A.
点评: 考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就更容易得到答案.
3.一个几何体的三视图如图所示,这个几何体是( )
A. 棱柱 B.圆柱 C.圆锥 D. 球
考点: 由三视图判断几何体.
分析: 根据三视图确定该几何体是圆柱体.
解答: 解:根据主视图和左视图为矩形可判断出该几何体是柱体,
根据俯视图是圆可判断出该几何体为圆柱.
故选:B.
点评: 本题考查由三视图确定几何体的形状,主要考查学生空间想象能力及对立体图形的认识.
4.某几何体的三视图如图所示,则这个几何体是( )
A. 圆柱 B.正方体 C.球 D. 圆锥
考点: 由三视图判断几何体.
分析: 由主视图和左视图确定是柱体,锥体还是球体,再由俯视图确定具体形状.
解答: 解:根据主视图和左视图为三角形判断出是锥体,根据俯视图是圆形可判断出这个几何体应该是圆锥,
故选:D.
点评: 主视图和左视图的大致轮廓为三角形的几何体为锥体,俯视图为圆就是圆锥.
5.如图所示的主视图、左视图、俯视图是下列哪个物体的三视图( )
A. B. C. D.
考点: 由三视图判断几何体.
分析: 根据三视图想象立体图形,从主视图可以看出左边的一列有两个,左视图可以看出左边的一列后面一行有两个,俯视图中右边的一列有两排,综合起来可得解.
解答: 解:从主视图可以看出左边的一列有两个,右边的两列只有一个;
从左视图可以看出左边的一列后面一行有两个,右边的一列只有一个;
从俯视图可以看出右边的一列有两排,右边的两列只有一排(第二排).
故选:A.
点评: 本题考查由三视图想象立体图形.做这类题时要借助三种视图表示物体的特点,从主视图上弄清物体的上下和左右形状;从俯视图上弄清物体的左右和前后形状;从左视图上弄清楚物体的上下和前后形状,综合分析,合理猜想,结合生活经验描绘出草图后,再检验是否符合题意.
6.某几何体的三视图如图所示,这个几何体是( )
A. 圆柱 B.三棱柱 C.长方体 D. 圆锥
考点: 由三视图判断几何体.
专题: 常规题型.
分析: 主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
解答: 解:由于主视图和左视图为长方形可得此几何体为柱体,
由俯视图为长方形可得为长方体.
故选:C.
点评: 本题考查了由三视图来判断几何体,还考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间的想象能力.
7.如图是由5个小立方块所搭成的几何体的俯视图,小正方形中的数字表示该位置小立方块的个数,这个几何体的主视图是( )
A. B. C. D.
考点: 由三视图判断几何体;简单组合体的三视图.
分析: 先细心观察原立体图形中正方体的位置关系,从正面看去,一共三列,左边有1竖列,中间有2竖列,右边是1竖列,结合四个选项选出答案.
解答: 解:从正面看去,一共三列,左边有1竖列,中间有2竖列,右边是1竖列.
故选:B.
点评: 本题考查了由三视图判断几何体及简单组合体的三视图,重点考查几何体的三视图及空间想象能力.
8.已知一个几何体的三视图如图所示,则该几何体是( )
A. 圆柱 B.圆锥 C.球 D. 棱柱
考点: 由三视图判断几何体.
分析: 主视图、左视图、俯视图是分别从物体正面、左面和上面看所得到的图形,从而得出答案.
解答: 解:俯视图为圆的几何体为球,圆锥,圆柱,再根据其他视图,可知此几何体为圆柱.
故选:A.
点评: 本题考查由三视图确定几何体的形状,主要考查学生空间想象能力.
二.填空题(共6小题)
9.一个几何体,是由许多规格相同的小正方体堆积而成的,其正视图、左视图如图所示,要摆成这样的图形,最少需用 7 个正方体.
考点: 由三视图判断几何体.
分析: 根据主视图、左视图是分别从物体正面、左面看,所得到的图形,结合本题进行分析即可.
解答: 解:根据三视图可得:第二层有2个小正方块,根据主视图和左视图可得第一层最少有5个正方体,故最少需用7块正方体;
故答案为7.
点评: 此题考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“主视图疯狂盖,左视图拆违章”就更容易得到答案.
10.如图是一个几何体的三个视图,则这个几何体的表面积为 24π .(结果保留π)
考点: 由三视图判断几何体;几何体的表面积.
分析: 根据三视图正视图以及左视图都为矩形,底面是圆形,则可想象出这是一个圆柱体.表面积=侧面积+底面积×2.
解答: 解:∵圆柱的直径为4,高为4,
∴表面积=2π×(×4)×4+π×(×4)2×2=24π.
故答案为:24π.
点评: 考查了由三视图判断几何体和几何体的表面积,本题难点是确定几何体的形状,关键是找到等量关系里相应的量.
11.一个由大小相同的正方体构成的几何体的三视图如图,这个几何体是由 4 个正方体组成的.
考点: 由三视图判断几何体.
分析: 根据三视图,该几何体的主视图以及俯视图可确定该几何体共有两行3列,故可得出该几何体的小正方体的个数.
解答: 解:综合三视图,我们可得出,这个几何体的底层应该有3个小正方体,第二层应该有1个小正方体,
因此搭成这个几何体的小正方体的个数为3+1=4个,
故答案为:4.
点评: 本题意在考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就更容易得到答案.
12.如图是一个几何体的三视图,若这个几何体的体积是36,则它的表面积是 72 .
考点: 由三视图判断几何体.
专题: 压轴题.
分析: 根据主视图与左视图得出长方体的边长,再利用图形的体积得出它的高,进而得出表面积.
解答: 解:∵由主视图得出长方体的长是6,宽是2,这个几何体的体积是36,
∴设高为h,则6×2×h=36,
解得:h=3,
∴它的表面积是:2×3×2+2×6×2+3×6×2=72.
故答案为:72.
点评: 此题主要考查了利用三视图判断几何体的边长,得出图形的高是解题关键.
13.如图,一个几何体是由大小相同的小正方体焊接而成,其主视图、俯视图、左视图都是“田”字形,则焊接该几何体所需小正方体的个数最少为 4个 .
考点: 由三视图判断几何体.
分析: 主视图、俯视图、左视图是分别从物体正面、上面、左面看所得到的图形.
解答: 解:利用一个几何体是由大小相同的小正方体焊接而成,
综合主视图、俯视图、左视图,底层最少有2个小立方体,第二层最少有2个小立方体,
因此搭成这个几何体的小正方体的个数最少是4个.
故答案为:4个.
点评: 本题考查由三视图判断几何体,根据题目中要求的以最少的小正方体搭建这个几何体,可以想象出左视图的样子,然后根据“俯视图打地基,正视图疯狂盖,左视图拆违章”很容易就知道小正方体的个数.
14.由一些完全相同的小正方体搭成的几何体的主视图和左视图如图所示,则组成这个几何体的小正方体的个数可能是 4或5或6或7 .
考点: 由三视图判断几何体.
分析: 易得这个几何体共有2层,由左视图可得第一层立方体的个数,由主视图可得第二层立方体的可能的个数,相加即可.
解答: 解:由题中所给出的主视图知物体共三列,且左侧一列高两层,右侧一列最高一层;
由左视图可知左侧两行,右侧一行,于是,可确定左侧只有一个小正方体,而右侧可能是一行单层一行两层,出可能两行都是两层.
所以图中的小正方体最少4块,最多7块.
故答案为:4或5或6或7.
点评: 本题主要考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就更容易得到答案.
三.解答题(共6小题)
15.某工厂要加工一批茶叶罐,设计者给出了茶叶罐的三视图,如图,请你按照三视图确定制作每个密封罐所需钢板的面积.(单位:毫米)
考点: 由三视图判断几何体;圆柱的计算.
分析: 首先利用几何体的三视图确定该几何体的形状,然后计算其表面积.
解答: 解:由三视图可知茶叶罐的形状为圆柱体,并且茶叶罐的底面直径2R为100毫米,
高H为150毫米,
∵每个密封罐所需钢板的面积即为该圆柱体的表面积,
∴S表面积=2πR2+2πRH
=2π×502+2π×50×150
=20000π(毫米2).
答:制作每个密封罐所需钢板的面积为20000π毫米2.
点评: 此题主要考查了由三视图确定几何体和求几何体的面积与体积,难点是找到等量关系里相应的量.
16.某物体的三视图如图:
(1)此物体是什么体;
(2)求此物体的全面积.
考点: 由三视图判断几何体.
专题: 数形结合.
分析: 考查立体图形的三视图,圆柱的全面积的求法及公式的应用.
解答: 解:(1)根据三视图的知识,主视图以及左视图都为矩形,俯视图是一个圆,故可判断出该几何体为圆柱.(2分)
(2)根据圆柱的全面积公式可得,20π×40+2×π×102=1000π(6分).
点评: 注意立体图形三视图的看法,圆柱的全面积的计算.
17.右图是一个立体图形的三视图,请写出这个立体图形的名称,并计算这个立体图形的体积.(结果保留π)
考点: 由三视图判断几何体.
专题: 几何图形问题;压轴题.
分析: 从三视图可以看正视图以及左视图为矩形,而俯视图为圆形,故可以得出该立体图形为圆柱.由三视图可以圆柱的半径,长和高,易求体积.
解答: 解:该立体图形为圆柱,
∵圆柱的底面半径r=5,高h=10,
∴圆柱的体积V=πr2h=π×52×10=250π(立方单位).
答:所以立体图形的体积为250π立方单位.
点评: 考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查;圆柱体积公式=底面积×高.
18.如图是一个几何体的三视图,其中主视图、左视图都是腰为13cm,底为10cm的等腰三角形,求这个几何体的体积.
考点: 由三视图判断几何体.
分析: 由几何体的主视图和左视图都是等腰三角形,俯视图是圆,可以判断这个几何体是圆锥,求出圆锥的高,然后根据圆锥的体积公式求解即可.
解答: 解:由三视图可知此几何体是圆锥,
依题意知母线长l=13,底面半径r=5,
所以底面上的高h=,
∴圆锥的体积=πr2 h
=
=100π.
点评: 本题主要考查三视图的知识和圆锥体积的计算,解决此类图的关键是由三视图得到立体图形.
19.有一些大小相同的小正方体组成的简单几何体,从不同方向看到的平面图形如图所示,请你猜一猜组成这个几何体的小正方体的个数.
考点: 由三视图判断几何体.
分析: 根据三视图的知识,该几何体共有两列三行组成,底面有5个正方体,第二层有最少2个最多4个,第三层有1个,相加即可求解.
解答: 解:该几何体共有两列三行组成,底面有5个正方体,第二层有最少2个最多4个,第三层有1个,
5+2+1=8(个),
5+4+1=10(个).
答:组成这个几何体的小正方体的个数是8个或9个或10个.
点评: 本题考查对三视图的理解应用及空间想象能力.可从主视图上分清物体的上下和左右的层数,从俯视图上分清物体的左右和前后位置,综合上述分析数出小立方块的个数.
20.如图是由几个棱长为1cm的小立方块搭成的几何体从上往下看的平面图形,小立方块中的数字表示该位置上小立方块的个数,求出这个几何体的体积.
考点: 由三视图判断几何体.
分析: 先根据正方体的体积公式:V=l3,计算出一个正方体的体积,再数出几何体中小立方块的个数,相乘即可求解.
解答: 解:(1×1×1)×(3+4+2+1)
=1×10
=10(cm3)
答:这个几何体的体积是10cm3.
点评: 考查了由三视图判断几何体,关键是熟悉正方体的体积公式,得到几何体中小立方块的个数.
一.选择题(共8小题)
1.如图是由几个相同的小正方体搭成的几何体的三视图,则搭成这个几何体的小正方体的个数是( )
A. 4个 B.5个 C.6个 D. 7个
2.若图是由几个相同的小正方体搭成的几何体的主视图和俯视图,则搭成这个几何体的小正方体的个数最少是( )
A. 6 B.8 C.10 D. 12
3.一个几何体的三视图如图所示,这个几何体是( )
A. 棱柱 B.圆柱 C.圆锥 D. 球
4.某几何体的三视图如图所示,则这个几何体是( )
A. 圆柱 B.正方体 C.球 D. 圆锥
5.如图所示的主视图、左视图、俯视图是下列哪个物体的三视图( )
A. B. C. D.
6.某几何体的三视图如图所示,这个几何体是( )
A. 圆柱 B.三棱柱 C 长方体 D. 圆锥
7.如图是由5个小立方块所搭成的几何体的俯视图,小正方形中的数字表示该位置小立方块的个数,这个几何体的主视图是( )
A. B. C. D.
8.已知一个几何体的三视图如图所示,则该几何体是( )
A. 圆柱 B.圆锥 C.球 D. 棱柱
二.填空题(共6小题)
9.一个几何体,是由许多规格相同的小正方体堆积而成的,其正视图、左视图如图所示,要摆成这样的图形,最少需用 _________ 个正方体.
10.如图是一个几何体的三个视图,则这个几何体的表面积为 _________ .(结果保留π)
11.一个由大小相同的正方体构成的几何体的三视图如图,这个几何体是由 _________ 个正方体组成的.
12如图是一个几何体的三视图,若这个几何体的体积是36,则它的表面积是 _________ .
13.如图,一个几何体是由大小相同的小正方体焊接而成,其主视图、俯视图、左视图都是“田”字形,则焊接该几何体所需小正方体的个数最少为 _________ .
14.由一些完全相同的小正方体搭成的几何体的主视图和左视图如图所示,则组成这个几何体的小正方体的个数可能是 _________ .
三.解答题(共6小题)
15.某工厂要加工一批茶叶罐,设计者给出了茶叶罐的三视图,如图,请你按照三视图确定制作每个密封罐所需钢板的面积.(单位:毫米)
16.某物体的三视图如图:
(1)此物体是什么体;
(2)求此物体的全面积.
17.右图是一个立体图形的三视图,请写出这个立体图形的名称,并计算这个立体图形的体积.(结果保留π)
18.如图是一个几何体的三视图,其中主视图、左视图都是腰为13cm,底为10cm的等腰三角形,求这个几何体的体积.
19.有一些大小相同的小正方体组成的简单几何体,从不同方向看到的平面图形如图所示,请你猜一猜组成这个几何体的小正方体的个数.
20.如图是由几个棱长为1cm的小立方块搭成的几何体从上往下看的平面图形,小立方块中的数字表示该位置上小立方块的个数,求出这个几何体的体积.
第四章图形的初步认识4.2.2由视图到立体图形
参考答案与试题解析
一.选择题(共8小题)
1.如图是由几个相同的小正方体搭成的几何体的三视图,则搭成这个几何体的小正方体的个数是( )
A. 4个 B.5个 C.6个 D. 7个
考点: 由三视图判断几何体.
分析: 根据给出的几何体,通过动手操作,观察可得答案为4,也可以根据画三视图的方法,发挥空间想象能力,直接想象出每个位置正方体的数目,再加上来.
解答: 解:由三视图可得,需要的小正方体的数目:1+2+1=4.如图:
故选:A.
点评: 本题考查了几何体的三视图及空间想象能力.
2.若图是由几个相同的小正方体搭成的几何体的主视图和俯视图,则搭成这个几何体的小正方体的个数最少是( )
A. 6 B.8 C.10 D. 12
考点: 由三视图判断几何体.
专题: 几何图形问题.
分析: 根据主视图以及俯视图,可得出共有2行,根据俯视图可得出该几何体由2列组成,故可得出小正方体最少块数.
解答: 解:综合主视图和俯视图,底层最少有4个小立方体,第二层最少有2个小立方体,
因此搭成这个几何体的小正方体的个数最少是6个.
故选A.
点评: 考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就更容易得到答案.
3.一个几何体的三视图如图所示,这个几何体是( )
A. 棱柱 B.圆柱 C.圆锥 D. 球
考点: 由三视图判断几何体.
分析: 根据三视图确定该几何体是圆柱体.
解答: 解:根据主视图和左视图为矩形可判断出该几何体是柱体,
根据俯视图是圆可判断出该几何体为圆柱.
故选:B.
点评: 本题考查由三视图确定几何体的形状,主要考查学生空间想象能力及对立体图形的认识.
4.某几何体的三视图如图所示,则这个几何体是( )
A. 圆柱 B.正方体 C.球 D. 圆锥
考点: 由三视图判断几何体.
分析: 由主视图和左视图确定是柱体,锥体还是球体,再由俯视图确定具体形状.
解答: 解:根据主视图和左视图为三角形判断出是锥体,根据俯视图是圆形可判断出这个几何体应该是圆锥,
故选:D.
点评: 主视图和左视图的大致轮廓为三角形的几何体为锥体,俯视图为圆就是圆锥.
5.如图所示的主视图、左视图、俯视图是下列哪个物体的三视图( )
A. B. C. D.
考点: 由三视图判断几何体.
分析: 根据三视图想象立体图形,从主视图可以看出左边的一列有两个,左视图可以看出左边的一列后面一行有两个,俯视图中右边的一列有两排,综合起来可得解.
解答: 解:从主视图可以看出左边的一列有两个,右边的两列只有一个;
从左视图可以看出左边的一列后面一行有两个,右边的一列只有一个;
从俯视图可以看出右边的一列有两排,右边的两列只有一排(第二排).
故选:A.
点评: 本题考查由三视图想象立体图形.做这类题时要借助三种视图表示物体的特点,从主视图上弄清物体的上下和左右形状;从俯视图上弄清物体的左右和前后形状;从左视图上弄清楚物体的上下和前后形状,综合分析,合理猜想,结合生活经验描绘出草图后,再检验是否符合题意.
6.某几何体的三视图如图所示,这个几何体是( )
A. 圆柱 B.三棱柱 C.长方体 D. 圆锥
考点: 由三视图判断几何体.
专题: 常规题型.
分析: 主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
解答: 解:由于主视图和左视图为长方形可得此几何体为柱体,
由俯视图为长方形可得为长方体.
故选:C.
点评: 本题考查了由三视图来判断几何体,还考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间的想象能力.
7.如图是由5个小立方块所搭成的几何体的俯视图,小正方形中的数字表示该位置小立方块的个数,这个几何体的主视图是( )
A. B. C. D.
考点: 由三视图判断几何体;简单组合体的三视图.
分析: 先细心观察原立体图形中正方体的位置关系,从正面看去,一共三列,左边有1竖列,中间有2竖列,右边是1竖列,结合四个选项选出答案.
解答: 解:从正面看去,一共三列,左边有1竖列,中间有2竖列,右边是1竖列.
故选:B.
点评: 本题考查了由三视图判断几何体及简单组合体的三视图,重点考查几何体的三视图及空间想象能力.
8.已知一个几何体的三视图如图所示,则该几何体是( )
A. 圆柱 B.圆锥 C.球 D. 棱柱
考点: 由三视图判断几何体.
分析: 主视图、左视图、俯视图是分别从物体正面、左面和上面看所得到的图形,从而得出答案.
解答: 解:俯视图为圆的几何体为球,圆锥,圆柱,再根据其他视图,可知此几何体为圆柱.
故选:A.
点评: 本题考查由三视图确定几何体的形状,主要考查学生空间想象能力.
二.填空题(共6小题)
9.一个几何体,是由许多规格相同的小正方体堆积而成的,其正视图、左视图如图所示,要摆成这样的图形,最少需用 7 个正方体.
考点: 由三视图判断几何体.
分析: 根据主视图、左视图是分别从物体正面、左面看,所得到的图形,结合本题进行分析即可.
解答: 解:根据三视图可得:第二层有2个小正方块,根据主视图和左视图可得第一层最少有5个正方体,故最少需用7块正方体;
故答案为7.
点评: 此题考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“主视图疯狂盖,左视图拆违章”就更容易得到答案.
10.如图是一个几何体的三个视图,则这个几何体的表面积为 24π .(结果保留π)
考点: 由三视图判断几何体;几何体的表面积.
分析: 根据三视图正视图以及左视图都为矩形,底面是圆形,则可想象出这是一个圆柱体.表面积=侧面积+底面积×2.
解答: 解:∵圆柱的直径为4,高为4,
∴表面积=2π×(×4)×4+π×(×4)2×2=24π.
故答案为:24π.
点评: 考查了由三视图判断几何体和几何体的表面积,本题难点是确定几何体的形状,关键是找到等量关系里相应的量.
11.一个由大小相同的正方体构成的几何体的三视图如图,这个几何体是由 4 个正方体组成的.
考点: 由三视图判断几何体.
分析: 根据三视图,该几何体的主视图以及俯视图可确定该几何体共有两行3列,故可得出该几何体的小正方体的个数.
解答: 解:综合三视图,我们可得出,这个几何体的底层应该有3个小正方体,第二层应该有1个小正方体,
因此搭成这个几何体的小正方体的个数为3+1=4个,
故答案为:4.
点评: 本题意在考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就更容易得到答案.
12.如图是一个几何体的三视图,若这个几何体的体积是36,则它的表面积是 72 .
考点: 由三视图判断几何体.
专题: 压轴题.
分析: 根据主视图与左视图得出长方体的边长,再利用图形的体积得出它的高,进而得出表面积.
解答: 解:∵由主视图得出长方体的长是6,宽是2,这个几何体的体积是36,
∴设高为h,则6×2×h=36,
解得:h=3,
∴它的表面积是:2×3×2+2×6×2+3×6×2=72.
故答案为:72.
点评: 此题主要考查了利用三视图判断几何体的边长,得出图形的高是解题关键.
13.如图,一个几何体是由大小相同的小正方体焊接而成,其主视图、俯视图、左视图都是“田”字形,则焊接该几何体所需小正方体的个数最少为 4个 .
考点: 由三视图判断几何体.
分析: 主视图、俯视图、左视图是分别从物体正面、上面、左面看所得到的图形.
解答: 解:利用一个几何体是由大小相同的小正方体焊接而成,
综合主视图、俯视图、左视图,底层最少有2个小立方体,第二层最少有2个小立方体,
因此搭成这个几何体的小正方体的个数最少是4个.
故答案为:4个.
点评: 本题考查由三视图判断几何体,根据题目中要求的以最少的小正方体搭建这个几何体,可以想象出左视图的样子,然后根据“俯视图打地基,正视图疯狂盖,左视图拆违章”很容易就知道小正方体的个数.
14.由一些完全相同的小正方体搭成的几何体的主视图和左视图如图所示,则组成这个几何体的小正方体的个数可能是 4或5或6或7 .
考点: 由三视图判断几何体.
分析: 易得这个几何体共有2层,由左视图可得第一层立方体的个数,由主视图可得第二层立方体的可能的个数,相加即可.
解答: 解:由题中所给出的主视图知物体共三列,且左侧一列高两层,右侧一列最高一层;
由左视图可知左侧两行,右侧一行,于是,可确定左侧只有一个小正方体,而右侧可能是一行单层一行两层,出可能两行都是两层.
所以图中的小正方体最少4块,最多7块.
故答案为:4或5或6或7.
点评: 本题主要考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就更容易得到答案.
三.解答题(共6小题)
15.某工厂要加工一批茶叶罐,设计者给出了茶叶罐的三视图,如图,请你按照三视图确定制作每个密封罐所需钢板的面积.(单位:毫米)
考点: 由三视图判断几何体;圆柱的计算.
分析: 首先利用几何体的三视图确定该几何体的形状,然后计算其表面积.
解答: 解:由三视图可知茶叶罐的形状为圆柱体,并且茶叶罐的底面直径2R为100毫米,
高H为150毫米,
∵每个密封罐所需钢板的面积即为该圆柱体的表面积,
∴S表面积=2πR2+2πRH
=2π×502+2π×50×150
=20000π(毫米2).
答:制作每个密封罐所需钢板的面积为20000π毫米2.
点评: 此题主要考查了由三视图确定几何体和求几何体的面积与体积,难点是找到等量关系里相应的量.
16.某物体的三视图如图:
(1)此物体是什么体;
(2)求此物体的全面积.
考点: 由三视图判断几何体.
专题: 数形结合.
分析: 考查立体图形的三视图,圆柱的全面积的求法及公式的应用.
解答: 解:(1)根据三视图的知识,主视图以及左视图都为矩形,俯视图是一个圆,故可判断出该几何体为圆柱.(2分)
(2)根据圆柱的全面积公式可得,20π×40+2×π×102=1000π(6分).
点评: 注意立体图形三视图的看法,圆柱的全面积的计算.
17.右图是一个立体图形的三视图,请写出这个立体图形的名称,并计算这个立体图形的体积.(结果保留π)
考点: 由三视图判断几何体.
专题: 几何图形问题;压轴题.
分析: 从三视图可以看正视图以及左视图为矩形,而俯视图为圆形,故可以得出该立体图形为圆柱.由三视图可以圆柱的半径,长和高,易求体积.
解答: 解:该立体图形为圆柱,
∵圆柱的底面半径r=5,高h=10,
∴圆柱的体积V=πr2h=π×52×10=250π(立方单位).
答:所以立体图形的体积为250π立方单位.
点评: 考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查;圆柱体积公式=底面积×高.
18.如图是一个几何体的三视图,其中主视图、左视图都是腰为13cm,底为10cm的等腰三角形,求这个几何体的体积.
考点: 由三视图判断几何体.
分析: 由几何体的主视图和左视图都是等腰三角形,俯视图是圆,可以判断这个几何体是圆锥,求出圆锥的高,然后根据圆锥的体积公式求解即可.
解答: 解:由三视图可知此几何体是圆锥,
依题意知母线长l=13,底面半径r=5,
所以底面上的高h=,
∴圆锥的体积=πr2 h
=
=100π.
点评: 本题主要考查三视图的知识和圆锥体积的计算,解决此类图的关键是由三视图得到立体图形.
19.有一些大小相同的小正方体组成的简单几何体,从不同方向看到的平面图形如图所示,请你猜一猜组成这个几何体的小正方体的个数.
考点: 由三视图判断几何体.
分析: 根据三视图的知识,该几何体共有两列三行组成,底面有5个正方体,第二层有最少2个最多4个,第三层有1个,相加即可求解.
解答: 解:该几何体共有两列三行组成,底面有5个正方体,第二层有最少2个最多4个,第三层有1个,
5+2+1=8(个),
5+4+1=10(个).
答:组成这个几何体的小正方体的个数是8个或9个或10个.
点评: 本题考查对三视图的理解应用及空间想象能力.可从主视图上分清物体的上下和左右的层数,从俯视图上分清物体的左右和前后位置,综合上述分析数出小立方块的个数.
20.如图是由几个棱长为1cm的小立方块搭成的几何体从上往下看的平面图形,小立方块中的数字表示该位置上小立方块的个数,求出这个几何体的体积.
考点: 由三视图判断几何体.
分析: 先根据正方体的体积公式:V=l3,计算出一个正方体的体积,再数出几何体中小立方块的个数,相乘即可求解.
解答: 解:(1×1×1)×(3+4+2+1)
=1×10
=10(cm3)
答:这个几何体的体积是10cm3.
点评: 考查了由三视图判断几何体,关键是熟悉正方体的体积公式,得到几何体中小立方块的个数.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
