4.1.1认识立体图形跟踪训练(含详细解析)
文档属性
| 名称 | 4.1.1认识立体图形跟踪训练(含详细解析) |  | |
| 格式 | zip | ||
| 文件大小 | 455.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-24 13:25:47 | ||
图片预览


文档简介
第四章图形的认识4.1.1认识立体图形
一.选择题(共9小题)
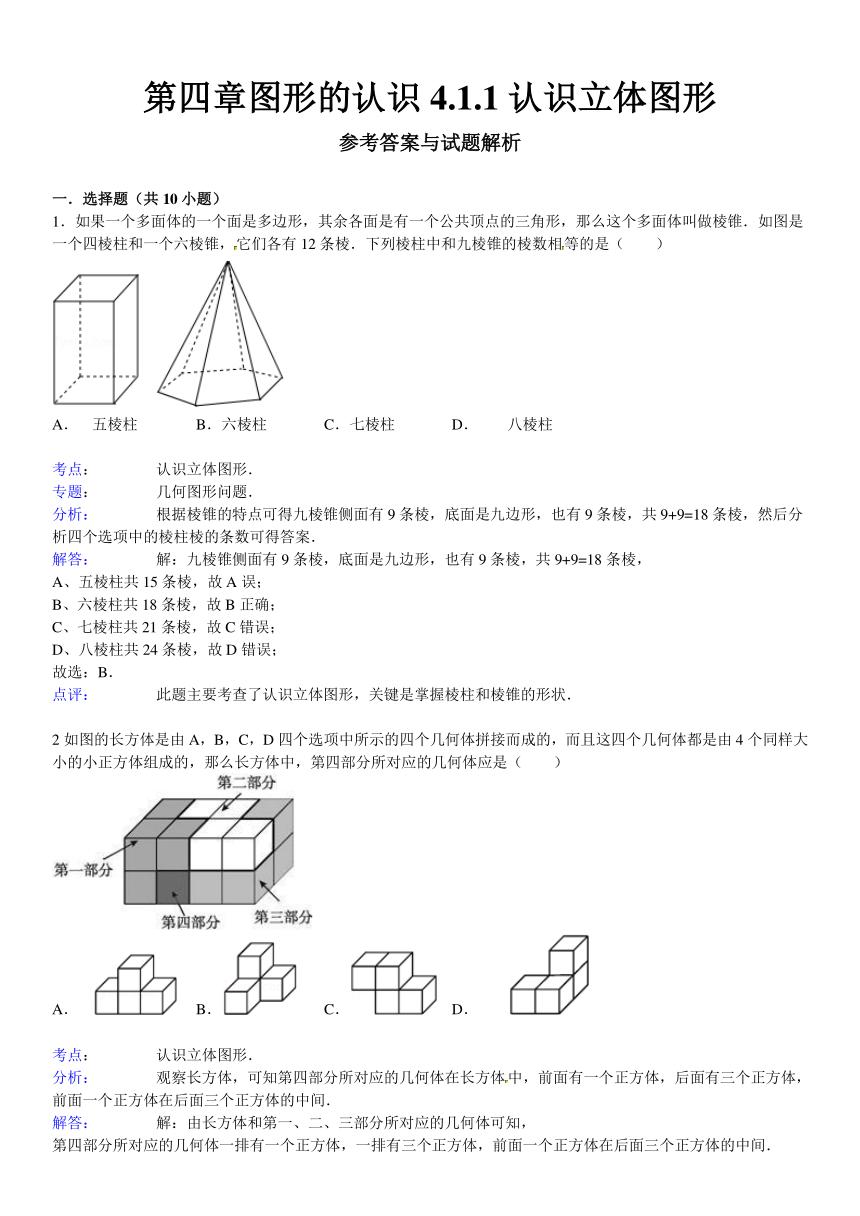
1.如果一个多面体的一个面是多边形,其余各面是有一个公共顶点的三角形,那么这个多面体叫做棱锥.如图是一个四棱柱和一个六棱锥,它们各有12条棱.下列棱柱中和九棱锥的棱数相等的是( )
A.五棱柱 B.六棱柱 C.七棱柱 D. 八棱柱
2.如图的长方体是由A,B,C,D四个选项中所示的四个几何体拼接而成的,而且这四个几何体都是由4个同样大小的小正方体组成的,那么长方体中,第四部分所对应的几何体应是( )
A. B. C. D.
3.如图,在长方体ABCD﹣EFGH中,与棱AD平行的平面共有( )
A. 1个 B.2个 C.3个 D. 4个
4.直四棱柱,长方体和正方体之间的包含关系是( )
A. B C. D.
5.下列物体的形状类似于球体的是( )
A. 茶杯 B.羽毛球 C.乒乓球 D. 白炽灯泡
6.由棱长为1的小正方体组成新的大正方体,如果不允许切割,至少要几个小正方体( )
A. 4个 B. 8个 C. 16个 D. 27个
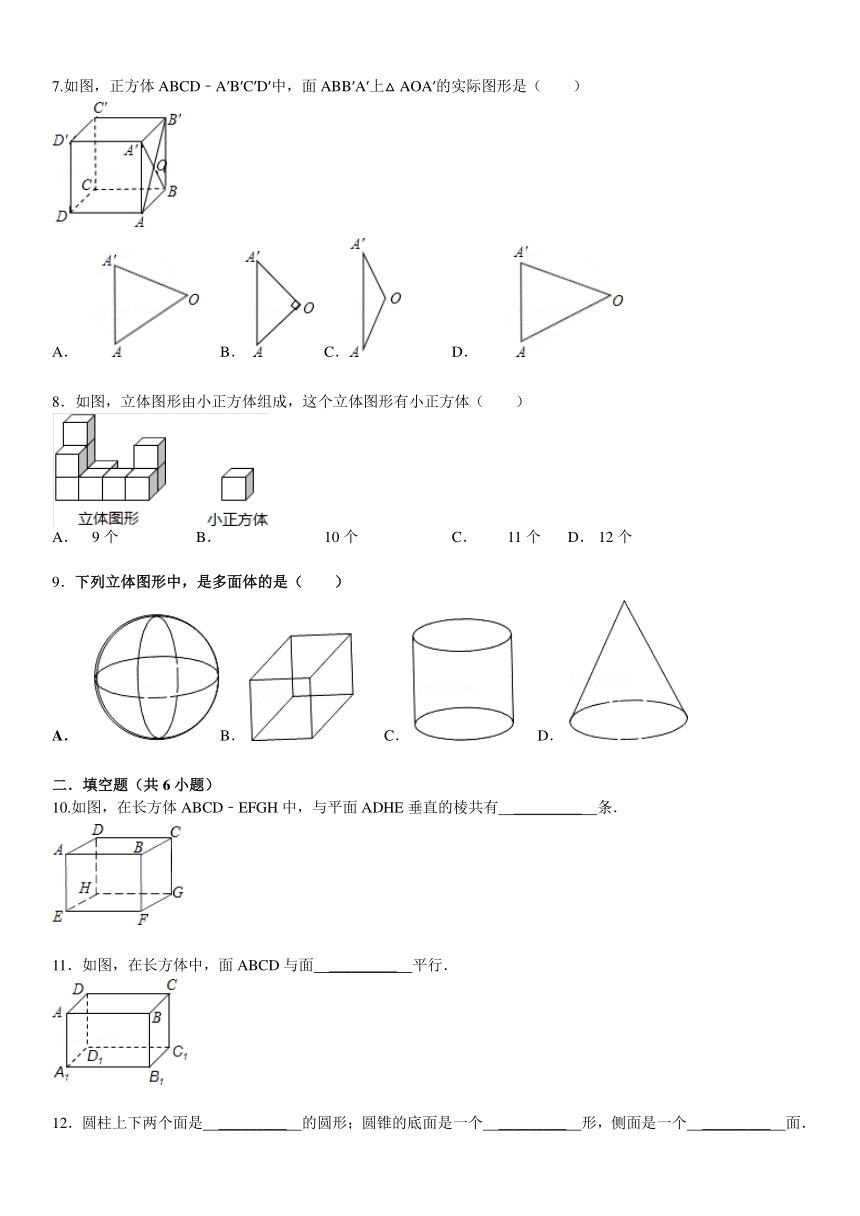
7.如图,正方体ABCD﹣A′B′C′D′中,面ABB′A′上△AOA′的实际图形是( )
A. B. C. D.
8.如图,立体图形由小正方体组成,这个立体图形有小正方体( )
A. 9个 B. 10个 C. 11个 D. 12个
9.下列立体图形中,是多面体的是( )
A. B. C. D.
二.填空题(共6小题)
10.如图,在长方体ABCD﹣EFGH中,与平面ADHE垂直的棱共有 _________ 条.
11.如图,在长方体中,面ABCD与面 _________ 平行.
12.圆柱上下两个面是 _________ 的圆形;圆锥的底面是一个 _________ 形,侧面是一个 _________ 面.
13.从棱长为4a的正方体中,挖去一个棱长为2a的小正方体,则该几何体的体积是 _________ .
14.下列说法中正确的有 _________ 个.
①棱锥的底面边数和侧面数相等;
②正方体和长方体是特殊的四棱柱,也是特殊的四面体;
③长方体是四棱柱,四棱柱也是长方体.
15.如图,在每个几何体下面写出它们的名称 _________ .
三.解答题(共6小题)
16.如图是由一个正方体和一个长方体组成的组合体.
(1)请你用代数式表示这个组合体的体积;
(2)请你说出它是几次几项式.
17.如图,画出8个立体图形,请你找出与图②具有相同特征的图形,并说出相同的特征是什么?
18.观察图中的圆柱和棱柱,通过想象回答下列问题:
(1)该圆柱和棱柱各由几个面组成?这些面是平面还是曲面?
(2)该圆柱的侧面与底面相交形成几条线?这些线是直线还是曲线?
(3)该棱柱的侧面与下底面相交形成几条线?
(4)该棱柱共有几个顶点?经过一个顶点有几条棱?
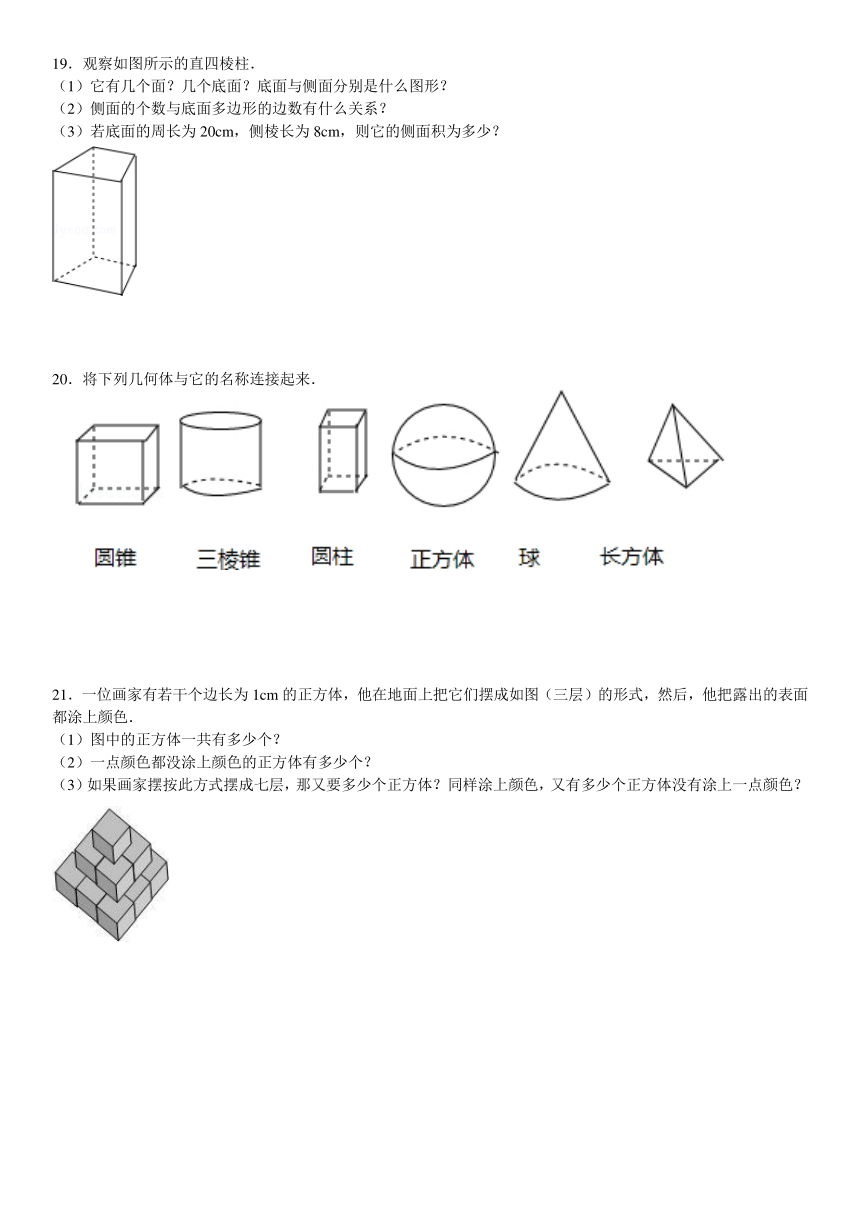
19.观察如图所示的直四棱柱.
(1)它有几个面?几个底面?底面与侧面分别是什么图形?
(2)侧面的个数与底面多边形的边数有什么关系?
(3)若底面的周长为20cm,侧棱长为8cm,则它的侧面积为多少?
20.将下列几何体与它的名称连接起来.
21.一位画家有若干个边长为1cm的正方体,他在地面上把它们摆成如图(三层)的形式,然后,他把露出的表面都涂上颜色.
(1)图中的正方体一共有多少个?
(2)一点颜色都没涂上颜色的正方体有多少个?
(3)如果画家摆按此方式摆成七层,那又要多少个正方体?同样涂上颜色,又有多少个正方体没有涂上一点颜色?
第四章图形的认识4.1.1认识立体图形
参考答案与试题解析
一.选择题(共10小题)
1.如果一个多面体的一个面是多边形,其余各面是有一个公共顶点的三角形,那么这个多面体叫做棱锥.如图是一个四棱柱和一个六棱锥,它们各有12条棱.下列棱柱中和九棱锥的棱数相等的是( )
A. 五棱柱 B.六棱柱 C.七棱柱 D. 八棱柱
考点: 认识立体图形.
专题: 几何图形问题.
分析: 根据棱锥的特点可得九棱锥侧面有9条棱,底面是九边形,也有9条棱,共9+9=18条棱,然后分析四个选项中的棱柱棱的条数可得答案.
解答: 解:九棱锥侧面有9条棱,底面是九边形,也有9条棱,共9+9=18条棱,
A、五棱柱共15条棱,故A误;
B、六棱柱共18条棱,故B正确;
C、七棱柱共21条棱,故C错误;
D、八棱柱共24条棱,故D错误;
故选:B.
点评: 此题主要考查了认识立体图形,关键是掌握棱柱和棱锥的形状.
2如图的长方体是由A,B,C,D四个选项中所示的四个几何体拼接而成的,而且这四个几何体都是由4个同样大小的小正方体组成的,那么长方体中,第四部分所对应的几何体应是( )
A. B. C. D.
考点: 认识立体图形.
分析: 观察长方体,可知第四部分所对应的几何体在长方体中,前面有一个正方体,后面有三个正方体,前面一个正方体在后面三个正方体的中间.
解答: 解:由长方体和第一、二、三部分所对应的几何体可知,
第四部分所对应的几何体一排有一个正方体,一排有三个正方体,前面一个正方体在后面三个正方体的中间.
故选A.
点评: 本题考查了认识立体图形,找到长方体中,第四部分所对应的几何体的形状是解题的关键.
3.如图,在长方体ABCD﹣EFGH中,与棱AD平行的平面共有( )
A. 1个 B. 2个 C. 3个 D. 4个
考点: 认识立体图形.
分析: 根据图示,我们可以看出,与AD相交的面有前面、后面、左面、下面四个面,只有上面和右面与其平行,解答即可.
解答: 解:观察可知,AD平行的平面有BCGF、EFGH两个面,故选B.
点评: 正确理解平行的概念是解题的关键.
4.直四棱柱,长方体和正方体之间的包含关系是( )
A B. C. D.
考点: 认识立体图形.
分析: 根据正方体,长方体,直四棱柱的概念和定义即可解.
解答: 解:正方体是特殊的长方体,长方体又是特殊的直四棱柱
故选:A.
点评: 本题考查了直四棱柱,长方体和正方体之间的包含关系.
5.下列物体的形状类似于球体的是( )
A. 茶杯 B. 羽毛球 C. 乒乓球 D. 白炽灯泡
考点: 认识立体图形.
分析: 根据球的形状与特点即可解答.
解答: 解:根据日常生活常识可知乒乓球是球体.
故选:C.
点评: 熟练掌握常见立体图形的特征,是解决此类问题的关键.
6.由棱长为1的小正方体组成新的大正方体,如果不允许切割,至少要几个小正方体( )
A. 4个 B. 8个 C. 16个 D. 27个
考点: 认识立体图形.
专题: 压轴题.
分析: 本题要求所得到的正方体最小,则每条棱是由两条小正方体的边组成.
解答: 解:根据以上分析要组成新的正方体至少要2×2×2=8个.
故选B.
点评: 本题主要考查空间想象能力,解决的关键是要能想象出正方体的形状.
7.如图,正方体ABCD﹣A′B′C′D′中,面ABB′A′上△AOA′的实际图形是( )
A. B. C. D.
考点: 认识立体图形.
分析: 结合正方体的特点,根据围成正方体6个面都是正方形,再由正方形的性质判断△AOA′的实际图形.
解答: 解:因为围成正方体6个面都是正方形,且正方形的对角线垂直平分,所以△AOA′是等腰直角三角形.
故选B.
点评: 本题考查了立体图形的认识,属于基础题型.解题的关键是熟记正方体和正方形的性质.
8.如图,立体图形由小正方体组成,这个立体图形有小正方体( )
A. 9个 B.10个 C.11个 D. 12个
考点: 认识立体图形.
分析: 仔细观察图,从左向右依次相加即解.注意被挡住的一个.
解答: 解:这个立体图形有小正方体5+2+1+3=11个.
故选:C.
点评: 解决此类问题,注意不要忽略了被挡住的小正方体.
9.下列立体图形中,是多面体的是( )
A. B. C. D.
考点: 认识立体图形.
分析: 多面体指四个或四个以上多边形所围成的立体图形.
解答: 解:A、只有一个面是曲面;
B、有6个面故是多面体;
C、有3个面,一个曲面两个平面;
D、有2个面,一个曲面,一个平面.
故选B.
点评: 本题考查的是多面体的定义,关键点在于:多面体指四个或四个以上多边形所围成的立体图形.
二.填空题(共6小题)
10.如图,在长方体ABCD﹣EFGH中,与平面ADHE垂直的棱共有 4 条.
考点: 认识立体图形.
分析: 在长方体,棱与面之间的关系有平行和垂直两种.
解答: 解:与平面ADHE垂直的棱有:AB,DC,HG,EF.共4条.
故答案为4.
点评: 本题考查的知识点为:与一个平面内的一条直线垂直的直线就与这个平面垂直.
11.如图,在长方体中,面ABCD与面 A1B1C1D1 平行.
考点: 认识立体图形.
分析: 根据图形可直接得到答案.
解答: 解:根据图形可得面ABCD与面A1B1C1D1平行,
故答案为:A1B1C1D1.
点评: 此题主要考查了认识立体图形,题目比较简单.
12.圆柱上下两个面是 相等 的圆形;圆锥的底面是一个 圆 形,侧面是一个 扇形 面.
考点: 认识立体图形.
分析: 根据圆柱和圆锥的特征,即可进行解答.
解答: 解:由圆柱和圆锥的特征可以得知:圆柱的底面都是圆,并且大小一样,侧面是曲面;
圆锥的底面也是圆形,侧面是扇形面,
则圆柱上下两个面是相等的圆形;圆锥的底面是一个圆形,侧面是一个扇形面.
故答案为:相等;圆;扇形.
点评: 此题考查了对圆柱体和圆锥体的认识,正确记忆重点图形的形状是解题关键.
13.从棱长为4a的正方体中,挖去一个棱长为2a的小正方体,则该几何体的体积是 56a .
考点: 认识立体图形.
分析: 根据正方体的体积减去正方体的体积,可得答案.
解答: 解:V=(4a)3﹣(2a)3=64a3﹣8a3=56a3,
故答案为:56a3.
点评: 本题考查了认识立体图形,利用了正方体的体积.
14.下列说法中正确的有 1 个.
①棱锥的底面边数和侧面数相等;
②正方体和长方体是特殊的四棱柱,也是特殊的四面体;
③长方体是四棱柱,四棱柱也是长方体.
考点: 认识立体图形.
分析: 根据棱锥的特点,可判断①;根据长方体的特点,可判断②③.
解答: 解:①棱锥的底面边数和侧面数相等,故①说法正确;
②正方体和长方体是特殊的四棱柱,也是特殊的六面体,故②说法错误;
③长方体是四棱柱,四棱柱不一定是长方体,故③说法错误;
故答案为:1.
点评: 本题考查了认识立体图形,利用了长方体和四棱柱的关系.
15.如图,在每个几何体下面写出它们的名称 长方体、圆柱、三棱锥 .
考点: 认识立体图形.
分析: 根据所给图形的特征进行判断.
解答: 解:从左向右三个几何体的名称是:长方体、圆柱、三棱锥.故答案为长方体、圆柱、三棱锥.
点评: 熟记常见立体图形的特征,是解决此类问题的关键,此题属于简单题型.
三.解答题(共6小题)
16.如图是由一个正方体和一个长方体组成的组合体.
(1)请你用代数式表示这个组合体的体积;
(2)请你说出它是几次几项式.
考点: 认识立体图形;多项式.
分析: (1)根据正方体的体积公式,长方体的体积公式,可得组合体的体积;
(2)根据多项式的项与次数,可得多项式的表示方法.
解答: 解;(1)由题意,得
这个组合体的体积是:a3+a2b;
(2)a3+a2b是三次二项式.
点评: 本题考查了认识立体图形,利用了正方体的体积公式,长方体的体积公式.
17.如图,画出8个立体图形,请你找出与图②具有相同特征的图形,并说出相同的特征是什么?
考点: 认识立体图形.
分析: 根据立体图形的特点从形状的特征考虑.
解答: 解:图④、⑦与图②,相同的特征是:它们都是锥体.
点评: 本题考查了认识立体图形,题目简单但不容易解答,需熟悉立体图形的特点,找出与题目已经提供的特征不相同的共同特征.
18.观察图中的圆柱和棱柱,通过想象回答下列问题:
(1)该圆柱和棱柱各由几个面组成?这些面是平面还是曲面?
(2)该圆柱的侧面与底面相交形成几条线?这些线是直线还是曲线?
(3)该棱柱的侧面与下底面相交形成几条线?
(4)该棱柱共有几个顶点?经过一个顶点有几条棱?
考点: 认识立体图形.
分析: 根据立体图形可得圆柱有3个面,六棱柱有8个面,圆柱的侧面与底面相交形成曲线,棱柱的侧面与下底面相交形成6条线.
解答: 解:(1)圆柱有3个面,上下底为平面,侧面为曲面;六棱柱有8个面,都是平面;
(2)圆柱的侧面与底面相交形成2条线,是曲线;
(3)该棱柱的侧面与下底面相交形成6条线;
(4)棱柱共有12个顶点,经过一个顶点有3条棱.
点评: 此题主要考查了认识立体图形,根据图形的形状进行解答即可.
19.观察如图所示的直四棱柱.
(1)它有几个面?几个底面?底面与侧面分别是什么图形?
(2)侧面的个数与底面多边形的边数有什么关系?
(3)若底面的周长为20cm,侧棱长为8cm,则它的侧面积为多少?
考点: 认识立体图形;几何体的表面积.
分析: (1)(2)(3)根据直四棱柱的特征直接解答即可.(4)根据棱柱的侧面积公式:底面周长×高,进行计算.
解答: 解:(1)它有6个面,2个底面,底面是梯形,侧面是长方形;
(2)侧面的个数与底面多边形的边数相等都为4;
(3)它的侧面积为20×8=160cm2.
点评: 本题考查了立体图形.解题时勿忘记四棱柱的特征及展开图的特征.四棱柱是由四个长方形的侧面和上下两个底面组成.
20.将下列几何体与它的名称连接起来.
考点: 认识立体图形.
分析: 根据常见立体图形的特征直接连线即可.注意正确区分各个几何体的特征.
解答: 解:如图所示:
点评: 考查了认识立体图形,熟记常见立体图形的特征是解决此类问题的关键.此题属于简单题型.
21.一位画家有若干个边长为1cm的正方体,他在地面上把它们摆成如图(三层)的形式,然后,他把露出的表面都涂上颜色.
(1)图中的正方体一共有多少个?
(2)一点颜色都没涂上颜色的正方体有多少个?
(3)如果画家摆按此方式摆成七层,那又要多少个正方体?同样涂上颜色,又有多少个正方体没有涂上一点颜色?
考点: 认识立体图形.
分析: (1)图中的正方体一共的个数=三层的个数的和;
(2)观察图形可知最底层正中间一个没涂上颜色;
(3)观察图形可知最底层有72个正方体,第2层有62个正方体,第3层有52个正方体,第4层有42个正方体,第5层有32个正方体,第6层有22个正方体,第7层有12个正方体,相加即可求出摆成七层的正方体一共的个数;
没有涂上一点颜色的正方体第5层有12个正方体,第4层有22个正方体,第3层有32个正方体,第4层有42个正方体,最底层有52个正方体,相加即可求出.
解答: 解:(1)图中的正方体一共有1+4+9=14个;
(2)一点颜色都没涂上颜色的正方体有1个;
(3)七层的正方体一共的个数12+22+32+42+52+62+72=140个;
没有涂上一点颜色的正方体12+22+32+42+52=55个.
答:(1)图中的正方体一共有14个.
(2)一点颜色都没涂上颜色的正方体有1个.
(3)如果画家摆按此方式摆成七层,要140个正方体,同样涂上颜色,有55个正方体没有涂上一点颜色.
点评: 本题考查学生对简单几何图形的掌握情况,既避免了单纯依靠公式机械计算的做法,又体现了数学知识在现实生活、甚至娱乐中的运用,体现了数学学科的基础性.
一.选择题(共9小题)
1.如果一个多面体的一个面是多边形,其余各面是有一个公共顶点的三角形,那么这个多面体叫做棱锥.如图是一个四棱柱和一个六棱锥,它们各有12条棱.下列棱柱中和九棱锥的棱数相等的是( )
A.五棱柱 B.六棱柱 C.七棱柱 D. 八棱柱
2.如图的长方体是由A,B,C,D四个选项中所示的四个几何体拼接而成的,而且这四个几何体都是由4个同样大小的小正方体组成的,那么长方体中,第四部分所对应的几何体应是( )
A. B. C. D.
3.如图,在长方体ABCD﹣EFGH中,与棱AD平行的平面共有( )
A. 1个 B.2个 C.3个 D. 4个
4.直四棱柱,长方体和正方体之间的包含关系是( )
A. B C. D.
5.下列物体的形状类似于球体的是( )
A. 茶杯 B.羽毛球 C.乒乓球 D. 白炽灯泡
6.由棱长为1的小正方体组成新的大正方体,如果不允许切割,至少要几个小正方体( )
A. 4个 B. 8个 C. 16个 D. 27个
7.如图,正方体ABCD﹣A′B′C′D′中,面ABB′A′上△AOA′的实际图形是( )
A. B. C. D.
8.如图,立体图形由小正方体组成,这个立体图形有小正方体( )
A. 9个 B. 10个 C. 11个 D. 12个
9.下列立体图形中,是多面体的是( )
A. B. C. D.
二.填空题(共6小题)
10.如图,在长方体ABCD﹣EFGH中,与平面ADHE垂直的棱共有 _________ 条.
11.如图,在长方体中,面ABCD与面 _________ 平行.
12.圆柱上下两个面是 _________ 的圆形;圆锥的底面是一个 _________ 形,侧面是一个 _________ 面.
13.从棱长为4a的正方体中,挖去一个棱长为2a的小正方体,则该几何体的体积是 _________ .
14.下列说法中正确的有 _________ 个.
①棱锥的底面边数和侧面数相等;
②正方体和长方体是特殊的四棱柱,也是特殊的四面体;
③长方体是四棱柱,四棱柱也是长方体.
15.如图,在每个几何体下面写出它们的名称 _________ .
三.解答题(共6小题)
16.如图是由一个正方体和一个长方体组成的组合体.
(1)请你用代数式表示这个组合体的体积;
(2)请你说出它是几次几项式.
17.如图,画出8个立体图形,请你找出与图②具有相同特征的图形,并说出相同的特征是什么?
18.观察图中的圆柱和棱柱,通过想象回答下列问题:
(1)该圆柱和棱柱各由几个面组成?这些面是平面还是曲面?
(2)该圆柱的侧面与底面相交形成几条线?这些线是直线还是曲线?
(3)该棱柱的侧面与下底面相交形成几条线?
(4)该棱柱共有几个顶点?经过一个顶点有几条棱?
19.观察如图所示的直四棱柱.
(1)它有几个面?几个底面?底面与侧面分别是什么图形?
(2)侧面的个数与底面多边形的边数有什么关系?
(3)若底面的周长为20cm,侧棱长为8cm,则它的侧面积为多少?
20.将下列几何体与它的名称连接起来.
21.一位画家有若干个边长为1cm的正方体,他在地面上把它们摆成如图(三层)的形式,然后,他把露出的表面都涂上颜色.
(1)图中的正方体一共有多少个?
(2)一点颜色都没涂上颜色的正方体有多少个?
(3)如果画家摆按此方式摆成七层,那又要多少个正方体?同样涂上颜色,又有多少个正方体没有涂上一点颜色?
第四章图形的认识4.1.1认识立体图形
参考答案与试题解析
一.选择题(共10小题)
1.如果一个多面体的一个面是多边形,其余各面是有一个公共顶点的三角形,那么这个多面体叫做棱锥.如图是一个四棱柱和一个六棱锥,它们各有12条棱.下列棱柱中和九棱锥的棱数相等的是( )
A. 五棱柱 B.六棱柱 C.七棱柱 D. 八棱柱
考点: 认识立体图形.
专题: 几何图形问题.
分析: 根据棱锥的特点可得九棱锥侧面有9条棱,底面是九边形,也有9条棱,共9+9=18条棱,然后分析四个选项中的棱柱棱的条数可得答案.
解答: 解:九棱锥侧面有9条棱,底面是九边形,也有9条棱,共9+9=18条棱,
A、五棱柱共15条棱,故A误;
B、六棱柱共18条棱,故B正确;
C、七棱柱共21条棱,故C错误;
D、八棱柱共24条棱,故D错误;
故选:B.
点评: 此题主要考查了认识立体图形,关键是掌握棱柱和棱锥的形状.
2如图的长方体是由A,B,C,D四个选项中所示的四个几何体拼接而成的,而且这四个几何体都是由4个同样大小的小正方体组成的,那么长方体中,第四部分所对应的几何体应是( )
A. B. C. D.
考点: 认识立体图形.
分析: 观察长方体,可知第四部分所对应的几何体在长方体中,前面有一个正方体,后面有三个正方体,前面一个正方体在后面三个正方体的中间.
解答: 解:由长方体和第一、二、三部分所对应的几何体可知,
第四部分所对应的几何体一排有一个正方体,一排有三个正方体,前面一个正方体在后面三个正方体的中间.
故选A.
点评: 本题考查了认识立体图形,找到长方体中,第四部分所对应的几何体的形状是解题的关键.
3.如图,在长方体ABCD﹣EFGH中,与棱AD平行的平面共有( )
A. 1个 B. 2个 C. 3个 D. 4个
考点: 认识立体图形.
分析: 根据图示,我们可以看出,与AD相交的面有前面、后面、左面、下面四个面,只有上面和右面与其平行,解答即可.
解答: 解:观察可知,AD平行的平面有BCGF、EFGH两个面,故选B.
点评: 正确理解平行的概念是解题的关键.
4.直四棱柱,长方体和正方体之间的包含关系是( )
A B. C. D.
考点: 认识立体图形.
分析: 根据正方体,长方体,直四棱柱的概念和定义即可解.
解答: 解:正方体是特殊的长方体,长方体又是特殊的直四棱柱
故选:A.
点评: 本题考查了直四棱柱,长方体和正方体之间的包含关系.
5.下列物体的形状类似于球体的是( )
A. 茶杯 B. 羽毛球 C. 乒乓球 D. 白炽灯泡
考点: 认识立体图形.
分析: 根据球的形状与特点即可解答.
解答: 解:根据日常生活常识可知乒乓球是球体.
故选:C.
点评: 熟练掌握常见立体图形的特征,是解决此类问题的关键.
6.由棱长为1的小正方体组成新的大正方体,如果不允许切割,至少要几个小正方体( )
A. 4个 B. 8个 C. 16个 D. 27个
考点: 认识立体图形.
专题: 压轴题.
分析: 本题要求所得到的正方体最小,则每条棱是由两条小正方体的边组成.
解答: 解:根据以上分析要组成新的正方体至少要2×2×2=8个.
故选B.
点评: 本题主要考查空间想象能力,解决的关键是要能想象出正方体的形状.
7.如图,正方体ABCD﹣A′B′C′D′中,面ABB′A′上△AOA′的实际图形是( )
A. B. C. D.
考点: 认识立体图形.
分析: 结合正方体的特点,根据围成正方体6个面都是正方形,再由正方形的性质判断△AOA′的实际图形.
解答: 解:因为围成正方体6个面都是正方形,且正方形的对角线垂直平分,所以△AOA′是等腰直角三角形.
故选B.
点评: 本题考查了立体图形的认识,属于基础题型.解题的关键是熟记正方体和正方形的性质.
8.如图,立体图形由小正方体组成,这个立体图形有小正方体( )
A. 9个 B.10个 C.11个 D. 12个
考点: 认识立体图形.
分析: 仔细观察图,从左向右依次相加即解.注意被挡住的一个.
解答: 解:这个立体图形有小正方体5+2+1+3=11个.
故选:C.
点评: 解决此类问题,注意不要忽略了被挡住的小正方体.
9.下列立体图形中,是多面体的是( )
A. B. C. D.
考点: 认识立体图形.
分析: 多面体指四个或四个以上多边形所围成的立体图形.
解答: 解:A、只有一个面是曲面;
B、有6个面故是多面体;
C、有3个面,一个曲面两个平面;
D、有2个面,一个曲面,一个平面.
故选B.
点评: 本题考查的是多面体的定义,关键点在于:多面体指四个或四个以上多边形所围成的立体图形.
二.填空题(共6小题)
10.如图,在长方体ABCD﹣EFGH中,与平面ADHE垂直的棱共有 4 条.
考点: 认识立体图形.
分析: 在长方体,棱与面之间的关系有平行和垂直两种.
解答: 解:与平面ADHE垂直的棱有:AB,DC,HG,EF.共4条.
故答案为4.
点评: 本题考查的知识点为:与一个平面内的一条直线垂直的直线就与这个平面垂直.
11.如图,在长方体中,面ABCD与面 A1B1C1D1 平行.
考点: 认识立体图形.
分析: 根据图形可直接得到答案.
解答: 解:根据图形可得面ABCD与面A1B1C1D1平行,
故答案为:A1B1C1D1.
点评: 此题主要考查了认识立体图形,题目比较简单.
12.圆柱上下两个面是 相等 的圆形;圆锥的底面是一个 圆 形,侧面是一个 扇形 面.
考点: 认识立体图形.
分析: 根据圆柱和圆锥的特征,即可进行解答.
解答: 解:由圆柱和圆锥的特征可以得知:圆柱的底面都是圆,并且大小一样,侧面是曲面;
圆锥的底面也是圆形,侧面是扇形面,
则圆柱上下两个面是相等的圆形;圆锥的底面是一个圆形,侧面是一个扇形面.
故答案为:相等;圆;扇形.
点评: 此题考查了对圆柱体和圆锥体的认识,正确记忆重点图形的形状是解题关键.
13.从棱长为4a的正方体中,挖去一个棱长为2a的小正方体,则该几何体的体积是 56a .
考点: 认识立体图形.
分析: 根据正方体的体积减去正方体的体积,可得答案.
解答: 解:V=(4a)3﹣(2a)3=64a3﹣8a3=56a3,
故答案为:56a3.
点评: 本题考查了认识立体图形,利用了正方体的体积.
14.下列说法中正确的有 1 个.
①棱锥的底面边数和侧面数相等;
②正方体和长方体是特殊的四棱柱,也是特殊的四面体;
③长方体是四棱柱,四棱柱也是长方体.
考点: 认识立体图形.
分析: 根据棱锥的特点,可判断①;根据长方体的特点,可判断②③.
解答: 解:①棱锥的底面边数和侧面数相等,故①说法正确;
②正方体和长方体是特殊的四棱柱,也是特殊的六面体,故②说法错误;
③长方体是四棱柱,四棱柱不一定是长方体,故③说法错误;
故答案为:1.
点评: 本题考查了认识立体图形,利用了长方体和四棱柱的关系.
15.如图,在每个几何体下面写出它们的名称 长方体、圆柱、三棱锥 .
考点: 认识立体图形.
分析: 根据所给图形的特征进行判断.
解答: 解:从左向右三个几何体的名称是:长方体、圆柱、三棱锥.故答案为长方体、圆柱、三棱锥.
点评: 熟记常见立体图形的特征,是解决此类问题的关键,此题属于简单题型.
三.解答题(共6小题)
16.如图是由一个正方体和一个长方体组成的组合体.
(1)请你用代数式表示这个组合体的体积;
(2)请你说出它是几次几项式.
考点: 认识立体图形;多项式.
分析: (1)根据正方体的体积公式,长方体的体积公式,可得组合体的体积;
(2)根据多项式的项与次数,可得多项式的表示方法.
解答: 解;(1)由题意,得
这个组合体的体积是:a3+a2b;
(2)a3+a2b是三次二项式.
点评: 本题考查了认识立体图形,利用了正方体的体积公式,长方体的体积公式.
17.如图,画出8个立体图形,请你找出与图②具有相同特征的图形,并说出相同的特征是什么?
考点: 认识立体图形.
分析: 根据立体图形的特点从形状的特征考虑.
解答: 解:图④、⑦与图②,相同的特征是:它们都是锥体.
点评: 本题考查了认识立体图形,题目简单但不容易解答,需熟悉立体图形的特点,找出与题目已经提供的特征不相同的共同特征.
18.观察图中的圆柱和棱柱,通过想象回答下列问题:
(1)该圆柱和棱柱各由几个面组成?这些面是平面还是曲面?
(2)该圆柱的侧面与底面相交形成几条线?这些线是直线还是曲线?
(3)该棱柱的侧面与下底面相交形成几条线?
(4)该棱柱共有几个顶点?经过一个顶点有几条棱?
考点: 认识立体图形.
分析: 根据立体图形可得圆柱有3个面,六棱柱有8个面,圆柱的侧面与底面相交形成曲线,棱柱的侧面与下底面相交形成6条线.
解答: 解:(1)圆柱有3个面,上下底为平面,侧面为曲面;六棱柱有8个面,都是平面;
(2)圆柱的侧面与底面相交形成2条线,是曲线;
(3)该棱柱的侧面与下底面相交形成6条线;
(4)棱柱共有12个顶点,经过一个顶点有3条棱.
点评: 此题主要考查了认识立体图形,根据图形的形状进行解答即可.
19.观察如图所示的直四棱柱.
(1)它有几个面?几个底面?底面与侧面分别是什么图形?
(2)侧面的个数与底面多边形的边数有什么关系?
(3)若底面的周长为20cm,侧棱长为8cm,则它的侧面积为多少?
考点: 认识立体图形;几何体的表面积.
分析: (1)(2)(3)根据直四棱柱的特征直接解答即可.(4)根据棱柱的侧面积公式:底面周长×高,进行计算.
解答: 解:(1)它有6个面,2个底面,底面是梯形,侧面是长方形;
(2)侧面的个数与底面多边形的边数相等都为4;
(3)它的侧面积为20×8=160cm2.
点评: 本题考查了立体图形.解题时勿忘记四棱柱的特征及展开图的特征.四棱柱是由四个长方形的侧面和上下两个底面组成.
20.将下列几何体与它的名称连接起来.
考点: 认识立体图形.
分析: 根据常见立体图形的特征直接连线即可.注意正确区分各个几何体的特征.
解答: 解:如图所示:
点评: 考查了认识立体图形,熟记常见立体图形的特征是解决此类问题的关键.此题属于简单题型.
21.一位画家有若干个边长为1cm的正方体,他在地面上把它们摆成如图(三层)的形式,然后,他把露出的表面都涂上颜色.
(1)图中的正方体一共有多少个?
(2)一点颜色都没涂上颜色的正方体有多少个?
(3)如果画家摆按此方式摆成七层,那又要多少个正方体?同样涂上颜色,又有多少个正方体没有涂上一点颜色?
考点: 认识立体图形.
分析: (1)图中的正方体一共的个数=三层的个数的和;
(2)观察图形可知最底层正中间一个没涂上颜色;
(3)观察图形可知最底层有72个正方体,第2层有62个正方体,第3层有52个正方体,第4层有42个正方体,第5层有32个正方体,第6层有22个正方体,第7层有12个正方体,相加即可求出摆成七层的正方体一共的个数;
没有涂上一点颜色的正方体第5层有12个正方体,第4层有22个正方体,第3层有32个正方体,第4层有42个正方体,最底层有52个正方体,相加即可求出.
解答: 解:(1)图中的正方体一共有1+4+9=14个;
(2)一点颜色都没涂上颜色的正方体有1个;
(3)七层的正方体一共的个数12+22+32+42+52+62+72=140个;
没有涂上一点颜色的正方体12+22+32+42+52=55个.
答:(1)图中的正方体一共有14个.
(2)一点颜色都没涂上颜色的正方体有1个.
(3)如果画家摆按此方式摆成七层,要140个正方体,同样涂上颜色,有55个正方体没有涂上一点颜色.
点评: 本题考查学生对简单几何图形的掌握情况,既避免了单纯依靠公式机械计算的做法,又体现了数学知识在现实生活、甚至娱乐中的运用,体现了数学学科的基础性.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
