同角的基本关系式(湖北省宜昌市宜昌县)
文档属性
| 名称 | 同角的基本关系式(湖北省宜昌市宜昌县) |
|
|
| 格式 | rar | ||
| 文件大小 | 380.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-11-21 00:00:00 | ||
图片预览




文档简介
课件10张PPT。三角函数复习(2)一、内容结构主方图任意角的三角函数和差倍半公式三角函数的图象和性质已知三角函数值求角 本讲重点复习
任意角的三角函数1、诱导公式2、同角的基本关系式二、知识点★诱导公式的类型:
2kπ+α(k ∈z), π+α ,π-α ,-α ,2π-α(π/2的奇数倍)(π/2的偶数倍)★ ★诱导公式的记忆规律:奇变偶不变,符号看象限.你能正确写出各组诱导公式吗?诱导公式的作用是:
把求任意角的三角函数值,转化为求0到π/2角的三角函数值.1、诱导公式二、知识点2、同角三角函数的基本关系式①平方关系:
②商式关系:
③倒数关系:★公式的主要用途:
a)??已知一个角的三角函数 值,求此角的其他三角函数值
b)?化简同角三角函数式;
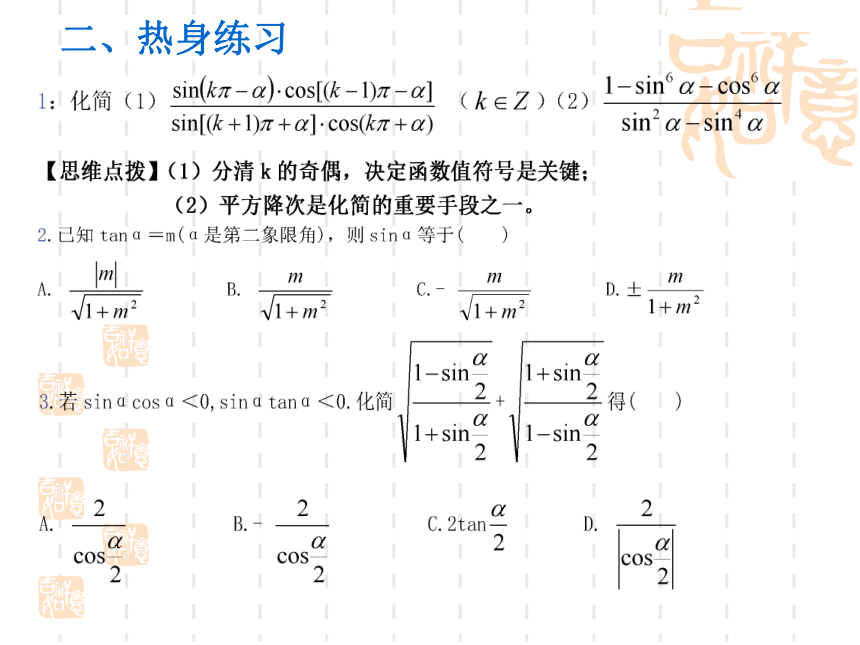
c)证明同角的三角恒等式。★ ★注意公式的正用、逆用与变用.二、热身练习三、典型例题分析【解题回顾】已知三角函数值求同角的其它三角函数值是一个基本题型,解答此问题过程中,通过基本关系式中正弦、余弦、正切之间的联系,必需开方且只需开方一次(有的题型根据已知条件可以尽量回避开方,使得问题轻松获解 ),根据α角所在象限,确定正负号的取舍.当给出的α的象限指定唯一,则此时一般有一解;当角α的象限没有定,可根据已知的函数值的符号确定α的象限,此时一般有二解(除轴上角外);当已知的三角函数值符号不确定,此时一般有四解(除轴上角.外).例2、:已知三、典型例题分析求 的值.【解题回顾】sinθ与cosθ通过公式sin2θ+cos2θ=1形成对立与统一的整体,它们的和sinθ+cosθ、差sinθ-cosθ、积sinθcosθ、商sinθ/cosθ(即tanθ)密切相联,如(sinθ+cosθ)2=1+2 sinθcosθ,
体现了数学的和谐、对称之美的特征.三、典型例题分析【解题回顾】视sinα,cos α等为“一次式”,sin2 α,sin αcos α等为“二次式”.
象此题中的“分式齐次式”、“齐次二项式”是典型的条件求值,一般化为含tanα
的式子.要注重数字“1”的代换,表面上看增加了运算,但同时它又可以将原表达式整体结构发生改变,给解决问题带来方面,故解题时,应给于足够的认识.【解题回顾】
★证等式常用方法:
(1)左边证明到右边或右边证明到左边(从繁到简为原则)
(2)两边向中间证
(3)分析法;
(4)用综合法
★ ★证等式的思路要灵活,根据等式两边式子结构特点,寻求思路.三、典型例题分析三、典型例题分析【解题回顾】根据目标式子无β的特点,采用消元思想,
三角平方关系式消元是一重要方法.四、小结
已知角的一个三角函数值求其他三角函数值时,应用平方关系确定符号是个难点,根据角的象限正确取舍;条件求值、恒等式的证明,三角式的化简等题型,要灵活使用公式,掌握常用技巧,思路要开阔,方法要灵活.
任意角的三角函数1、诱导公式2、同角的基本关系式二、知识点★诱导公式的类型:
2kπ+α(k ∈z), π+α ,π-α ,-α ,2π-α(π/2的奇数倍)(π/2的偶数倍)★ ★诱导公式的记忆规律:奇变偶不变,符号看象限.你能正确写出各组诱导公式吗?诱导公式的作用是:
把求任意角的三角函数值,转化为求0到π/2角的三角函数值.1、诱导公式二、知识点2、同角三角函数的基本关系式①平方关系:
②商式关系:
③倒数关系:★公式的主要用途:
a)??已知一个角的三角函数 值,求此角的其他三角函数值
b)?化简同角三角函数式;
c)证明同角的三角恒等式。★ ★注意公式的正用、逆用与变用.二、热身练习三、典型例题分析【解题回顾】已知三角函数值求同角的其它三角函数值是一个基本题型,解答此问题过程中,通过基本关系式中正弦、余弦、正切之间的联系,必需开方且只需开方一次(有的题型根据已知条件可以尽量回避开方,使得问题轻松获解 ),根据α角所在象限,确定正负号的取舍.当给出的α的象限指定唯一,则此时一般有一解;当角α的象限没有定,可根据已知的函数值的符号确定α的象限,此时一般有二解(除轴上角外);当已知的三角函数值符号不确定,此时一般有四解(除轴上角.外).例2、:已知三、典型例题分析求 的值.【解题回顾】sinθ与cosθ通过公式sin2θ+cos2θ=1形成对立与统一的整体,它们的和sinθ+cosθ、差sinθ-cosθ、积sinθcosθ、商sinθ/cosθ(即tanθ)密切相联,如(sinθ+cosθ)2=1+2 sinθcosθ,
体现了数学的和谐、对称之美的特征.三、典型例题分析【解题回顾】视sinα,cos α等为“一次式”,sin2 α,sin αcos α等为“二次式”.
象此题中的“分式齐次式”、“齐次二项式”是典型的条件求值,一般化为含tanα
的式子.要注重数字“1”的代换,表面上看增加了运算,但同时它又可以将原表达式整体结构发生改变,给解决问题带来方面,故解题时,应给于足够的认识.【解题回顾】
★证等式常用方法:
(1)左边证明到右边或右边证明到左边(从繁到简为原则)
(2)两边向中间证
(3)分析法;
(4)用综合法
★ ★证等式的思路要灵活,根据等式两边式子结构特点,寻求思路.三、典型例题分析三、典型例题分析【解题回顾】根据目标式子无β的特点,采用消元思想,
三角平方关系式消元是一重要方法.四、小结
已知角的一个三角函数值求其他三角函数值时,应用平方关系确定符号是个难点,根据角的象限正确取舍;条件求值、恒等式的证明,三角式的化简等题型,要灵活使用公式,掌握常用技巧,思路要开阔,方法要灵活.
