3.1列代数式 跟踪训练(含详细解析)
文档属性
| 名称 | 3.1列代数式 跟踪训练(含详细解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 196.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-24 14:41:56 | ||
图片预览




文档简介
第三章整式加减3.1列代数式
农安县合隆中学 徐亚惠
一.选择题(共10小题)
1.以下是代数式的是( )
A. m=ab B. (a+b)(a﹣b)=a2﹣b2 C. a+1 D. S=πR2
2.某商场举办促销活动,将原价x元的衣服改为(+1)元出售.下列叙述可作为此商场的促销标语的是( )
A. 原价打三四折再加一元 B. 原价打四三折再加一元
C. 原价加一元再打三四折 D. 原价打七五折再加一元
3.代数式a+b2读作( )
A. a与b的平方 B. a与b的和的平方
C. a的平方与b的平方的和 D. a与b的平方的和
4.用﹣a表示的一定是( )
A. 正数 B. 负数 C. 正数或负数 D. 以上都不对
5.下列代数式中符合书写要求的是( )
A. B. n2 C. a÷b D.
6.在2x2,1﹣2x=0,ab,a>0,0,,π中,是代数式的有( )
A. 5个 B. 4个 C. 3个 D. 2个
7.通信市场竞争日益激烈,某通信公司的手机 ( http: / / www.21cnjy.com )本地话费标准按原标准每分钟降低a元后,再次下调了20%,现在收费标准是每分钟b元,则原收费标准每分钟是( )
A. (a+b)元 B. (a﹣b)元 C. (a+5b)元 D. (a﹣5b)元
8.黄石市2011年6月份某日一天的温差为11℃,最高气温为t℃,则最低气温可表示为( )
A. (11+t)℃ B. (11﹣t)℃ C. (t﹣11)℃ D. (﹣t﹣11)℃
9.某工厂第一年生产a件产品,第二年比第一年增产了20%,则两年共生产产品的件数为( )
A. 0.2a B. a C. 1.2a D. 2.2a
二.填空题(共10小题)
10.吉林广播电视塔“五一”假期第一天接待游客m人,第二天接待游客n人,则这2天平均每天接待游客 .
11.学校购买了一批图书,共a箱,每箱有b册,将这批图书的一半捐给社区,则捐给社区的图书为 _________ 12.体育委员带了500元钱去买体育用品,已知一个足球a元,一个篮球b元.则代数式500﹣3a﹣2b表示的数为 13.实验中学初三年级12个班中共有团员a人,则表示的实际意义是 _________ .
14.代数式4a可表示的实际意义是 _________ 15若x2﹣2x=3,则代数式2x2﹣4x+3的值为 _________ .
16.若x=﹣1,则代数式x3﹣x2+4的值为 _________ .
17.小明t小时走了s千米的路,则他走这段路的平均速度是 _________ 千米/时.
18.今年五月份,由于H7N9禽流感的影响 ( http: / / www.21cnjy.com ),我市鸡肉的价格下降了10%,设鸡肉原来的价格为a元/千克,则五月份的价格为 _________ 元/千克.
19.对单项式“5x”,我 ( http: / / www.21cnjy.com )们可以这样理解:香蕉每千克5元,某人买了x千克,共付款“5x”元.请你结合生活实际,再给出“5x”的另一个合理解释为: _________ .
三.解答题(共9小题)
20.下列各式哪些是代数式?哪些不是代数式?
(1)3>2;(2)a+b=5;(3)a;(4)3;(5)5+4﹣1;(6)m米;(7)5x﹣3y
21.说出下列代数式的意义:
(1)2(a+3); (2)a2+b2; (3).
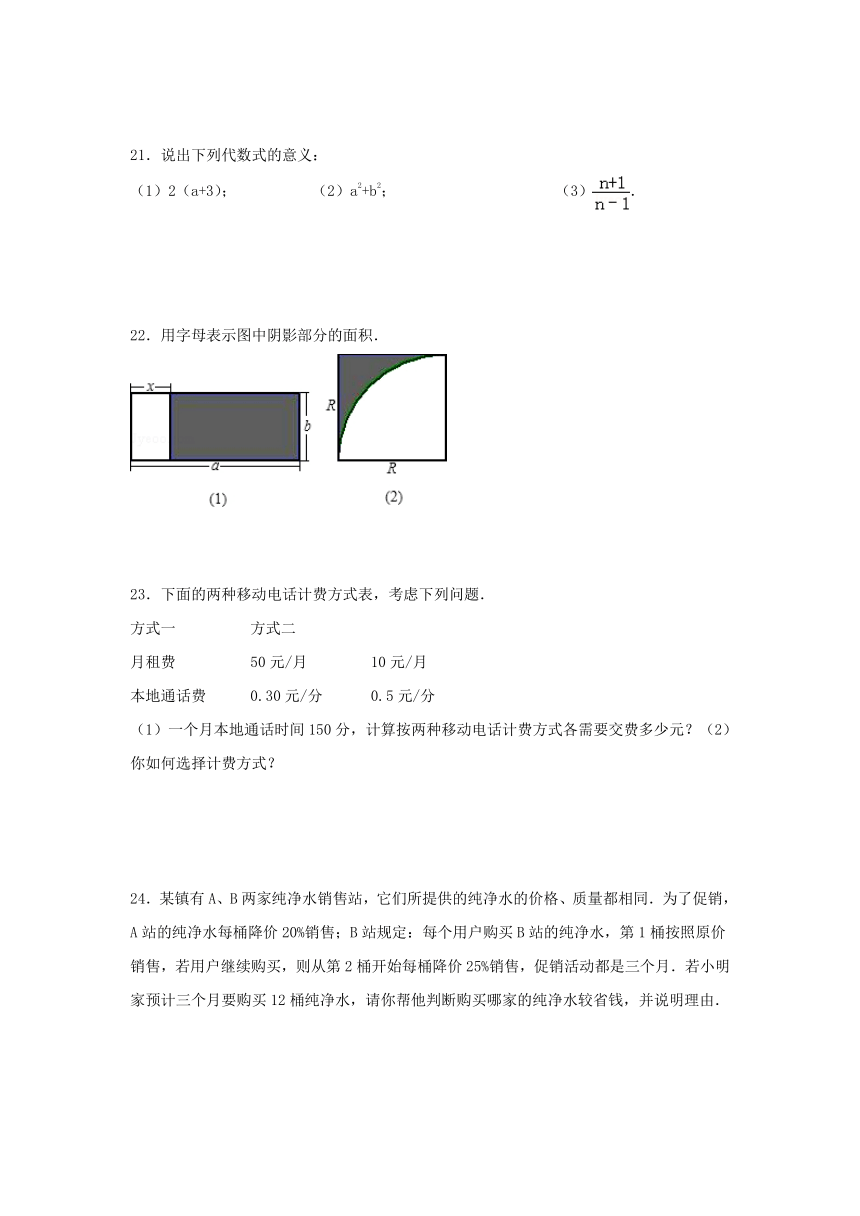
22.用字母表示图中阴影部分的面积.
( http: / / www.21cnjy.com )
23.下面的两种移动电话计费方式表,考虑下列问题.
方式一 方式二
月租费 50元/月 10元/月
本地通话费 0.30元/分 0.5元/分
一个月本地通话时间150分,计算按两种移动电话计费方式各需要交费多少元?(2)你如何选择计费方式?
24.某镇有A、B两家纯净水销售站,它 ( http: / / www.21cnjy.com )们所提供的纯净水的价格、质量都相同.为了促销,A站的纯净水每桶降价20%销售;B站规定:每个用户购买B站的纯净水,第1桶按照原价销售,若用户继续购买,则从第2桶开始每桶降价25%销售,促销活动都是三个月.若小明家预计三个月要购买12桶纯净水,请你帮他判断购买哪家的纯净水较省钱,并说明理由.
25.如果某三角形第一条边长为(2 ( http: / / www.21cnjy.com )a﹣b)cm,第二条边比第一条边长(a+b)cm,第三条边比第一条边的2倍少b(cm),求这个三角形的周长(用a、b的代数式表示).
26.某市电话拨号上网有两种收费方式,用户可以任选其一:
(A)计时制:0.05元每分钟; (B)包月制:60元每月(限一部个人住宅电话上网);
此外,每一种上网方式都得加收通信费0.02元每分钟.
(1)某用户某月上网的时间为x小时,请分别写出两种收费方式下该用户应该支付的费用;
(2)若某用户估计一个月内上网的时间为25小时,你认为采用哪种方式较为合算?
27.用如图所示正方形纸板制作一个无盖的长方体盒子,可在正方体的四角减去相同的正方形,剩余部分即可做成一个无盖的长方体形盒子.
(1)设正方形纸的边长为a,减去的小正方形的边长为x,请用a与x表示这个无盖长方体形盒子的容积;
(2)把正方形的纸板换成长为a,宽为b的长方形纸板,怎样做一个无盖长方体形盒子?画图说明你的做法;
(3)把(2)中做的长方体形盒子的容积用代数式表示出来;
(4)比较(1)和(3)的结果,说说它们的区别和联系.
( http: / / www.21cnjy.com )
(27题)
28.小明将连续的奇数1,3,5,7,9,…,排成如图所示的数阵,用一个矩形框框住其中的9个数,如图所示.
(1)矩形阴影框中的9个数的和与中间一个数存在怎样的关系?(直接写出笞案)
(2)若将矩形框上下左右移动,这个关系还成立吗?为什么?
( http: / / www.21cnjy.com )
第三章整式加减3.1列代数式
参考答案与试题解析
一.选择题(共9小题)
1.以下是代数式的是( )
A. m=ab B. (a+b)(a﹣b)=a2﹣b2 C. a+1 D. S=πR2
考点: 代数式.
分析: 用运算符号把数字与字母连接而成的式子叫做代数式.单独的一个数或一个字母也是代数式.
解答: 解:因为代数式中不含“=”号,所以是代数式的是C.
故选C.
点评: 代数式中不含“=”号.
2.某商场举办促销活动,将原价x元的衣服改为(+1)元出售.下列叙述可作为此商场的促销标语的是( )
A. 原价打三四折再加一元 B. 原价打四三折再加一元
C. 原价加一元再打三四折 D. 原价打七五折再加一元
考点: 代数式.
分析: 根据是0.75,是七五折,所以是七五折加1,然后直接选取答案.
解答: 解:∵+1元是七五折加1的意思,
∴标语应为:原价打七五折再加一元.
故选D.
点评: 本题考查打折销售的常识,x是七五折的意思.
3.代数式a+b2读作( )
A. a与b的平方 B. a与b的和的平方
C. a的平方与b的平方的和 D. a与b的平方的和
考点: 代数式.
分析: 根据代数式的特点来读.代数式a+b2是两项a与b2的和.
解答: 解:代数式a+b2读作:a与b的平方的和.
故选D.
点评: 此题考查了代数式的书写与读的联系,要求学生能根据题意写出代数式,又能根据代数式读出它所表示的意义.
4.用﹣a表示的一定是( )
A. 正数 B. 负数 C. 正数或负数 D. 以上都不对
考点: 代数式.
分析: ﹣a表示的有可能是A中说的正数,有可能B中说的负数,有可能C中说的正数或负数.
解答: 解:﹣a表示的有可能是A中说的正数,有可能B中说的负数,有可能C中说的正数或负数.
故选D.
点评: 本题考查了代数式,考查了实数范围内的数的正负以及表达情况.
5.下列代数式中符合书写要求的是( )
A. B. n2 C. a÷b D.
考点: 代数式.
专题: 计算题.
分析: 根据代数式的书写要求对各选项依次进行判断即可解答.
解答: 解:A、中的带分数要写成假分数;
B、中的2应写在字母的前面;
C、应写成分数的形式;
D、符合书写要求.
故选D.
点评: 本题主要考查代数式的书写要求:
(1)在代数式中出现的乘号,通常简写成“ ”或者省略不写;
(2)数字与字母相乘时,数字要写在字母的前面;
(3)在代数式中出现的除法运算,一般按照分数的写法来写.带分数要写成假分数的形式.
6.在2x2,1﹣2x=0,ab,a>0,0,,π中,是代数式的有( )
A. 5个 B. 4个 C. 3个 D. 2个
考点: 代数式.
分析: 代数式是有数和字母组成,表 ( http: / / www.21cnjy.com )示加、减、乘、除、乘方、开方等运算的式子,或含有字母的数学表达式,注意不能含有=、<、>、≤、≥、≈、≠等符号.
解答: 解:∵1﹣2x=0,a>0,含有=和>,所以不是代数式,
∴代数式的有2x2,ab,0,,π,共5个.
故选A.
点评: 此题主要考查了代数式的定义,掌握代数式的定义是本题的关键,注意含有=、<、>、≤、≥、≈、≠等符号的不是代数式.
7.通信市场竞争日益激烈,某通信公司的手机本 ( http: / / www.21cnjy.com )地话费标准按原标准每分钟降低a元后,再次下调了20%,现在收费标准是每分钟b元,则原收费标准每分钟是( )
A. (a+b)元 B. (a﹣b)元 C. (a+5b)元 D. (a﹣5b)元
考点: 列代数式.
专题: 压轴题.
分析: 首先表示出下调了20%后的价格,然后加上a元,即可得到.
解答: 解:b÷(1﹣20%)+a=a+b.
故选A.
点评: 本题考查了列代数式,正确理解题目中的关系是关键.
8.黄石市2011年6月份某日一天的温差为11℃,最高气温为t℃,则最低气温可表示为( )
A. (11+t)℃ B. (11﹣t)℃ C. (t﹣11)℃ D. (﹣t﹣11)℃
考点: 列代数式.
专题: 计算题.
分析: 由已知可知,最高气温﹣最低气温=温差,从而求出最低气温.
解答: 解:设最低气温为x℃,则:
t﹣x=11,
x=t﹣11.
故选C.
点评: 此题考查的知识点是列代数式,此题要明确温差就是最高气温减去最低气温.
9.某工厂第一年生产a件产品,第二年比第一年增产了20%,则两年共生产产品的件数为( )
A. 0.2a B. a C. 1.2a D. 2.2a
考点: 列代数式.
分析: 两年共生产产品的件数=第一年生产产品件数+第二年生产产品件数.
解答: 解:第二年生产产品件数为a×(1+20%)=1.2a,
∴两年共生产产品的件数为a+1.2a=2.2a,故选D.
点评: 解决问题的关键是读懂题意,找到所求的量的等量关系.注意应先求得第二年的生产的产品件数.
二.填空题(共10小题)
10.吉林广播电视塔“五一”假期第一天接待游客m人,第二天接待游客n人,则这2天平均每天接待游客 人(用含m、n的代数式表示).
考点: 列代数式.
分析: 用两天接待的游客总人数除以天数,即可得解.
解答: 解:2天平均每天接待游客.
故答案为:.
点评: 本题考查了列代数式,比较简单,熟练掌握平均数的求法是解题的关键.
11.学校购买了一批图书,共a箱,每箱有b册,将这批图书的一半捐给社区,则捐给社区的图书为 册(用含a、b的代数式表示).
考点: 列代数式.
分析: 首先根据题意可得这批图书共有ab册,它的一半就是册.
解答: 解:由题意得:这批图书共有ab册,
则图书的一半是:册.
故答案为:.
点评: 此题主要考查了列代数式,关键是弄清题目的意思,表示出这批图书的总数量,注意代数式的书写方法,除法要写成分数形式.
12.体育委员带了500元 ( http: / / www.21cnjy.com )钱去买体育用品,已知一个足球a元,一个篮球b元.则代数式500﹣3a﹣2b表示的数为 体育委员买了3个足球,2个篮球,剩余的经费 .
考点: 代数式.
专题: 应用题.
分析: 本题需先根据买一个足球a元,一个篮球b元的条件,表示出3a和2b的意义,最后得出正确答案即可.
解答: 解:∵买一个足球a元,一个篮球b元.
∴3a表示委员买了3个足球
2b表示买了2个篮球
∴代数式500﹣3a﹣2b:表示委员买了3个足球、2个篮球,剩余的经费.
故答案为:体育委员买了3个足球、2个篮球,剩余的经费
点评: 本题主要考查了列代数式,在解题时要根据题意表示出各项的意义是本题的关键.
13.实验中学初三年级12个班中共有团员a人,则表示的实际意义是 平均每班团员数 .
考点: 代数式.
专题: 压轴题.
分析: 总人数÷班级的个数=平均每班团员数.
解答: 解:表示的实际意义是平均每班团员数.
点评: 注意掌握代数式的实际意义.
14.代数式4a可表示的 ( http: / / www.21cnjy.com )实际意义是 答案不唯一,要求:符合代数式的意义,如:每去钢笔4元,买了a支钢笔所需的钱数,或正方形的边长为a,它的周长是4a.
考点: 代数式.
专题: 开放型.
分析: 根据代数式表示的意义和实际的联系编写场景即可.
解答: 解:答案不唯一.
如:每去钢笔4元,买了a支钢笔所需的钱数,
或正方形的边长为a,它的周长是4a.
点评: 此题综合考查代数式表示的意义和实际的联系.
15.若x2﹣2x=3,则代数式2x2﹣4x+3的值为 9 .
考点: 代数式求值.
专题: 计算题.
分析: 所求式子前两项提取2变形后,将已知等式代入计算即可求出值.
解答: 解:∵x2﹣2x=3,
∴2x2﹣4x+3=2(x2﹣2x)+3=6+3=9.
故答案为:9
点评: 此题考查了代数式求值,利用了整体代入的思想,是一道基本题型.
16.若x=﹣1,则代数式x3﹣x2+4的值为 2 .
考点: 代数式求值.
专题: 计算题.
分析: 把x=﹣1代入代数式进行计算即可得解.
解答: 解:x3﹣x2+4,
=(﹣1)3﹣(﹣1)2+4,
=﹣1﹣1+4,
=﹣2+4,
=2.
故答案为:2.
点评: 本题考查了代数式求值,把x的值代入进行计算即可得解,比较简单.
17.小明t小时走了s千米的路,则他走这段路的平均速度是 千米/时.
考点: 代数式.
分析: 根据速度的计算公式即可求得小明的平均速度.
解答: 解:小明走这段路的平均速度是千米/时.
点评: 本题考查了平均速度的计算.平均速度=总路程÷总时间.
18.今年五月份,由于H7N9禽流感的 ( http: / / www.21cnjy.com )影响,我市鸡肉的价格下降了10%,设鸡肉原来的价格为a元/千克,则五月份的价格为 0.9a 元/千克.
考点: 列代数式.
分析: 因为原来鸡肉价格为a元/千克,现在下降了10%,所以现在的价格为(1﹣10%)a,即0.9a元/千克.
解答: 解:∵原来鸡肉价格为a元/千克,现在下降了10%,
∴五月份的价格为a﹣10%a=(1﹣10%)a=0.9a,
故答案为:0.9a.
点评: 本题考查了列代数式的知识,解决 ( http: / / www.21cnjy.com )问题的关键是读懂题意,找到所求的量的等量关系.注意价格下降了10%就是指原来的价格减去原来价格的10%.
29.对单项式“5x”,我们可以这 ( http: / / www.21cnjy.com )样理解:香蕉每千克5元,某人买了x千克,共付款“5x”元.请你结合生活实际,再给出“5x”的另一个合理解释为: 某人的行走速度是x米/分,5分钟行走的路程. .
考点: 代数式.
专题: 开放型.
分析: 解释合理即可,答案不唯一.
解答: 解:对单项式“5x”,我们可以这样理解:某人的行走速度是x米/分,5分钟行走的路程.
点评: 此类问题应结合实际,根据代数式的特点解答.
三.解答题(共9小题)
20.下列各式哪些是代数式?哪些不是代数式?
(1)3>2;(2)a+b=5;(3)a;(4)3;(5)5+4﹣1;(6)m米;(7)5x﹣3y
考点: 代数式.
分析: 根据代数式的概念,用运算符号把数字与字母连接而成的式子叫做代数式.单独的一个数或一个字母也是代数式.
解答: 解:(1)、(2)中的“>”、“=”它们不是运算符号,因此(1)、(2)不是代数式.
(3)、(4)中a、3是代数式,因为单个数字和字母是代数式.
(5)中是加减运算符号把5、4、1连接起来,因此是代数式.
(6)m米含有单位名称,故不是代数式.
(7)5x﹣3y中由乘、减两种运算联起5、x、3、y,因此是代数式.
答:代数式有(3)(4)(5)(7);(1)(2)(6)不是代数式.
点评: 注意掌握代数式的定义.
21.说出下列代数式的意义:
(1)2(a+3);
(2)a2+b2;
(3).
考点: 代数式.
专题: 开放型.
分析: 说出下列代数式的意义,实际上就是把代数式用语言叙述出来.叙述时,要求既要表明运算的顺序,又要说出运算的最终结果.
解答: 解:(1)2(a+3)的意义是2与(a+3)的积;
(2)a2+b2的意义是a,b的平方的和;
(3)的意义是(n+1)除以(n﹣1)的商.
点评: 用语言表达代数式的意义,一定要理清代数式中含有的各种运算及其顺序.具体说法没有统一规定,以简明而不引起误会为出发点.
22.用字母表示图中阴影部分的面积.
( http: / / www.21cnjy.com )
考点: 代数式.
分析: (1)读图可得,阴影部分的面积=大长方形的面积﹣小长方形的面积;
(2)阴影部分的面积=正方形的面积﹣扇形的面积.
解答: 解:(1)阴影部分的面积=ab﹣bx;
(2)阴影部分的面积=R2﹣πR2.
点评: 解决问题的关键是读懂图,找到所求的阴影部分的面积和各部分之间的等量关系.
23.下面的两种移动电话计费方式表,考虑下列问题.
方式一 方式二
月租费 50元/月 10元/月
本地通话费 0.30元/分 0.5元/分
(1)一个月本地通话时间150分,计算按两种移动电话计费方式各需要交费多少元?
(2)你如何选择计费方式?为什么?(分类讨论)
考点: 有理数的混合运算;列代数式.
分析: (1)首先根据题意,计算出本地通话总计费,然后再加上月租费,即可推出两种激动电话计费各需要交费多少;
(2)要看我的电话一个月内的本地通话时间为多少分钟,首先设出通话时间为x,列出方程0.3x+50=0.5x+10,求出x,再进行分析即可.
解答: 解:(1)方式一:150×0.30+50=45+50=95(元),
方式二:150×0.5+10=75+10=85(元),
答:按方式一的计费方式需要交费95元,按方式二的计费方式需要交费85元,
(2)设一个月内本地通话x分钟时,两种通讯方式的费用相同,
∴0.3x+50=0.5x+10,
整理方程得:0.2x=40,
∴x=200.
∴若x<200分钟时,0.30x+50>0.5x+10,
若x>200分钟时,0.3x+50<0.5x+10,
答:若一个月内的电话时间多于200分钟,就选择计费方式一,
若一个月内的电话时间少于200分钟,就选择计费方式二,
若一个月内的电话时间等于200分钟,两种计费方式都可以选择.
点评: 本题主要考查有理数的混合运算,关键是求出两种通讯方式的费用相同时,一个月内的本地通话是多少分钟,找到此临界点.
24.某镇有A、B两家纯净水销售站,它们 ( http: / / www.21cnjy.com )所提供的纯净水的价格、质量都相同.为了促销,A站的纯净水每桶降价20%销售;B站规定:每个用户购买B站的纯净水,第1桶按照原价销售,若用户继续购买,则从第2桶开始每桶降价25%销售,促销活动都是三个月.若小明家预计三个月要购买12桶纯净水,请你帮他判断购买哪家的纯净水较省钱,并说明理由.
考点: 列代数式.
专题: 应用题;方案型.
分析: 缺少原价,可设原单价为a,那 ( http: / / www.21cnjy.com )么去A销售站需付费:原总价×(1﹣20%);在B站需花费的金额为:一桶原价+其余的原总价×(1﹣25%),然后进行比较.
解答: 解:设每桶纯净水的原价为a元,则购买12桶纯净水,
在A站需花费的金额为(1﹣20%)a 12=9.6a(元);
在B站需花费的金额为a+(1﹣25%)a 11=9.25a(元);
∵9.6a>9.25a,
∴小明家应选择到B家纯净水销售站购买纯净水,这样较省钱.
点评: 解决问题的关键是读懂题意,找到 ( http: / / www.21cnjy.com )所求的量的等量关系.要注意其中的关系:原总价×(1﹣20%);一桶原价+其余的原总价×(1﹣25%).
25.如果某三角形第一条边长为 ( http: / / www.21cnjy.com )(2a﹣b)cm,第二条边比第一条边长(a+b)cm,第三条边比第一条边的2倍少b(cm),求这个三角形的周长(用a、b的代数式表示).
考点: 列代数式.
专题: 应用题.
分析: 第二条边长为(2a﹣b)+(a+b),第三条边长为2(2a﹣b)﹣b,然后求三边的和即可.
解答: 解:周长=(2a﹣b)+[(2a﹣b)+(a+b)]+[2(2a﹣b)﹣b]
=2a﹣b+2a﹣b+a+b+4a﹣2b﹣b
=9a﹣4b.
点评: 解决问题的关键是读懂题意,找到所求的量的等量关系.本题只需仔细分析题意,进行多项式的加法运算即可.
26.某市电话拨号上网有两种收费方式,用户可以任选其一:
(A)计时制:0.05元每分钟;
(B)包月制:60元每月(限一部个人住宅电话上网);
此外,每一种上网方式都得加收通信费0.02元每分钟.
(1)某用户某月上网的时间为x小时,请分别写出两种收费方式下该用户应该支付的费用;
(2)若某用户估计一个月内上网的时间为25小时,你认为采用哪种方式较为合算?
考点: 列代数式.
分析: (1)首先统一时间单位,(A) ( http: / / www.21cnjy.com )计时制:每分钟(0.05+0.02)元×时间=花费;(B)包月制:60元+每分钟0.02元×时间=花费;
(2)把x=25代入(1)中的代数式计算出花费,进行比较即可.
解答: 解:(1)x小时=60x分钟,
(A)计时制:(0.05+0.02) 60x=0.07 60x=4.2x,
(B)包月制:60+0.02 60x=60+1.2x.
(2)A)计时制:4.2x=4.2×25=105(元),
(B)包月制:60+1.2x=60+1.2×25=90(元).
∵90<105,
∴用(B)方式较为合算.
点评: 此题主要考查了列代数式,并比较哪种花费便宜的问题,关键是弄清题意列出式子.
27.问题探究.
用如图所示正方形纸板制作一个无盖的长方体盒子,可在正方体的四角减去相同的正方形,剩余部分即可做成一个无盖的长方体形盒子.
(1)设正方形纸的边长为a,减去的小正方形的边长为x,请用a与x表示这个无盖长方体形盒子的容积;
(2)把正方形的纸板换成长为a,宽为b的长方形纸板,怎样做一个无盖长方体形盒子?画图说明你的做法;
(3)把(2)中做的长方体形盒子的容积用代数式表示出来;
(4)比较(1)和(3)的结果,说说它们的区别和联系.
( http: / / www.21cnjy.com )
考点: 列代数式.
分析: (1)观察图形可知底面长、宽都为(a﹣2x),高为x,用长方体的体积公式表示体积;
(2)在长方形纸板的四个角减去相同的正方形,剩余部分即可做成一个无盖的长方体形盒子;
(3)先设减去的正方形边长为x,然后求出长方体盒子的底面积,再乘以高即可得出答案;
(4)根据长方体和正方体的体积公式即可得出它们之间的区别和联系.
解答: 解:(1)依题意,长方体盒子容积为:(a﹣2x)2 x;
(2)画图如下:
( http: / / www.21cnjy.com )
(3)设减去的正方形边长为x,根据题意得:
(a﹣2x)(b﹣2x) x;
(4)(1)中底面积为正方形面积为(a﹣2 ( http: / / www.21cnjy.com )x)2,(3)中底面积为长方形,面积为(a﹣2x)(b﹣2x),高都为x,(3)中当a=b时即得到(1)中的结果.
点评: 此题考查了列代数式;本题关键是表示长方体的长、宽、高,再用体积公式计算.
28.小明将连续的奇数1,3,5,7,9,…,排成如图所示的数阵,用一个矩形框框住其中的9个数,如图所示.
(1)矩形阴影框中的9个数的和与中间一个数存在怎样的关系?(直接写出笞案)
(2)若将矩形框上下左右移动,这个关系还成立吗?为什么?
( http: / / www.21cnjy.com )
考点: 列代数式.
专题: 规律型.
分析: (1)将方框内的数字相加等于171,通过计算得出存在的关系.
(2)若将矩形框上下左右移动,可举两个实例证明是否成立.
解答: 解:(1)计算阴影框中9个数的和为,3+5+7+17+19+21+31+33+35=171,171÷19=9,
所以,矩形阴影框中的9个数的和是中间一个数的9倍;
(2)假设将矩形框向下移动一个格,则中间的数为33.
则9个数的和为,17+19+21+31+32+33+35+45+47+49=297,297÷33=9,
再假设将矩形框向左移动一个格,则中间的数为17,
则9个数的和为:1+3+5+15+17+19+29+31+33=153,153÷17=9.
所以这个关系还成立.
点评: 此题是通过计算得出存在的关系的,也可以通过观察总结出一定的规律进行解答.
农安县合隆中学 徐亚惠
一.选择题(共10小题)
1.以下是代数式的是( )
A. m=ab B. (a+b)(a﹣b)=a2﹣b2 C. a+1 D. S=πR2
2.某商场举办促销活动,将原价x元的衣服改为(+1)元出售.下列叙述可作为此商场的促销标语的是( )
A. 原价打三四折再加一元 B. 原价打四三折再加一元
C. 原价加一元再打三四折 D. 原价打七五折再加一元
3.代数式a+b2读作( )
A. a与b的平方 B. a与b的和的平方
C. a的平方与b的平方的和 D. a与b的平方的和
4.用﹣a表示的一定是( )
A. 正数 B. 负数 C. 正数或负数 D. 以上都不对
5.下列代数式中符合书写要求的是( )
A. B. n2 C. a÷b D.
6.在2x2,1﹣2x=0,ab,a>0,0,,π中,是代数式的有( )
A. 5个 B. 4个 C. 3个 D. 2个
7.通信市场竞争日益激烈,某通信公司的手机 ( http: / / www.21cnjy.com )本地话费标准按原标准每分钟降低a元后,再次下调了20%,现在收费标准是每分钟b元,则原收费标准每分钟是( )
A. (a+b)元 B. (a﹣b)元 C. (a+5b)元 D. (a﹣5b)元
8.黄石市2011年6月份某日一天的温差为11℃,最高气温为t℃,则最低气温可表示为( )
A. (11+t)℃ B. (11﹣t)℃ C. (t﹣11)℃ D. (﹣t﹣11)℃
9.某工厂第一年生产a件产品,第二年比第一年增产了20%,则两年共生产产品的件数为( )
A. 0.2a B. a C. 1.2a D. 2.2a
二.填空题(共10小题)
10.吉林广播电视塔“五一”假期第一天接待游客m人,第二天接待游客n人,则这2天平均每天接待游客 .
11.学校购买了一批图书,共a箱,每箱有b册,将这批图书的一半捐给社区,则捐给社区的图书为 _________ 12.体育委员带了500元钱去买体育用品,已知一个足球a元,一个篮球b元.则代数式500﹣3a﹣2b表示的数为 13.实验中学初三年级12个班中共有团员a人,则表示的实际意义是 _________ .
14.代数式4a可表示的实际意义是 _________ 15若x2﹣2x=3,则代数式2x2﹣4x+3的值为 _________ .
16.若x=﹣1,则代数式x3﹣x2+4的值为 _________ .
17.小明t小时走了s千米的路,则他走这段路的平均速度是 _________ 千米/时.
18.今年五月份,由于H7N9禽流感的影响 ( http: / / www.21cnjy.com ),我市鸡肉的价格下降了10%,设鸡肉原来的价格为a元/千克,则五月份的价格为 _________ 元/千克.
19.对单项式“5x”,我 ( http: / / www.21cnjy.com )们可以这样理解:香蕉每千克5元,某人买了x千克,共付款“5x”元.请你结合生活实际,再给出“5x”的另一个合理解释为: _________ .
三.解答题(共9小题)
20.下列各式哪些是代数式?哪些不是代数式?
(1)3>2;(2)a+b=5;(3)a;(4)3;(5)5+4﹣1;(6)m米;(7)5x﹣3y
21.说出下列代数式的意义:
(1)2(a+3); (2)a2+b2; (3).
22.用字母表示图中阴影部分的面积.
( http: / / www.21cnjy.com )
23.下面的两种移动电话计费方式表,考虑下列问题.
方式一 方式二
月租费 50元/月 10元/月
本地通话费 0.30元/分 0.5元/分
一个月本地通话时间150分,计算按两种移动电话计费方式各需要交费多少元?(2)你如何选择计费方式?
24.某镇有A、B两家纯净水销售站,它 ( http: / / www.21cnjy.com )们所提供的纯净水的价格、质量都相同.为了促销,A站的纯净水每桶降价20%销售;B站规定:每个用户购买B站的纯净水,第1桶按照原价销售,若用户继续购买,则从第2桶开始每桶降价25%销售,促销活动都是三个月.若小明家预计三个月要购买12桶纯净水,请你帮他判断购买哪家的纯净水较省钱,并说明理由.
25.如果某三角形第一条边长为(2 ( http: / / www.21cnjy.com )a﹣b)cm,第二条边比第一条边长(a+b)cm,第三条边比第一条边的2倍少b(cm),求这个三角形的周长(用a、b的代数式表示).
26.某市电话拨号上网有两种收费方式,用户可以任选其一:
(A)计时制:0.05元每分钟; (B)包月制:60元每月(限一部个人住宅电话上网);
此外,每一种上网方式都得加收通信费0.02元每分钟.
(1)某用户某月上网的时间为x小时,请分别写出两种收费方式下该用户应该支付的费用;
(2)若某用户估计一个月内上网的时间为25小时,你认为采用哪种方式较为合算?
27.用如图所示正方形纸板制作一个无盖的长方体盒子,可在正方体的四角减去相同的正方形,剩余部分即可做成一个无盖的长方体形盒子.
(1)设正方形纸的边长为a,减去的小正方形的边长为x,请用a与x表示这个无盖长方体形盒子的容积;
(2)把正方形的纸板换成长为a,宽为b的长方形纸板,怎样做一个无盖长方体形盒子?画图说明你的做法;
(3)把(2)中做的长方体形盒子的容积用代数式表示出来;
(4)比较(1)和(3)的结果,说说它们的区别和联系.
( http: / / www.21cnjy.com )
(27题)
28.小明将连续的奇数1,3,5,7,9,…,排成如图所示的数阵,用一个矩形框框住其中的9个数,如图所示.
(1)矩形阴影框中的9个数的和与中间一个数存在怎样的关系?(直接写出笞案)
(2)若将矩形框上下左右移动,这个关系还成立吗?为什么?
( http: / / www.21cnjy.com )
第三章整式加减3.1列代数式
参考答案与试题解析
一.选择题(共9小题)
1.以下是代数式的是( )
A. m=ab B. (a+b)(a﹣b)=a2﹣b2 C. a+1 D. S=πR2
考点: 代数式.
分析: 用运算符号把数字与字母连接而成的式子叫做代数式.单独的一个数或一个字母也是代数式.
解答: 解:因为代数式中不含“=”号,所以是代数式的是C.
故选C.
点评: 代数式中不含“=”号.
2.某商场举办促销活动,将原价x元的衣服改为(+1)元出售.下列叙述可作为此商场的促销标语的是( )
A. 原价打三四折再加一元 B. 原价打四三折再加一元
C. 原价加一元再打三四折 D. 原价打七五折再加一元
考点: 代数式.
分析: 根据是0.75,是七五折,所以是七五折加1,然后直接选取答案.
解答: 解:∵+1元是七五折加1的意思,
∴标语应为:原价打七五折再加一元.
故选D.
点评: 本题考查打折销售的常识,x是七五折的意思.
3.代数式a+b2读作( )
A. a与b的平方 B. a与b的和的平方
C. a的平方与b的平方的和 D. a与b的平方的和
考点: 代数式.
分析: 根据代数式的特点来读.代数式a+b2是两项a与b2的和.
解答: 解:代数式a+b2读作:a与b的平方的和.
故选D.
点评: 此题考查了代数式的书写与读的联系,要求学生能根据题意写出代数式,又能根据代数式读出它所表示的意义.
4.用﹣a表示的一定是( )
A. 正数 B. 负数 C. 正数或负数 D. 以上都不对
考点: 代数式.
分析: ﹣a表示的有可能是A中说的正数,有可能B中说的负数,有可能C中说的正数或负数.
解答: 解:﹣a表示的有可能是A中说的正数,有可能B中说的负数,有可能C中说的正数或负数.
故选D.
点评: 本题考查了代数式,考查了实数范围内的数的正负以及表达情况.
5.下列代数式中符合书写要求的是( )
A. B. n2 C. a÷b D.
考点: 代数式.
专题: 计算题.
分析: 根据代数式的书写要求对各选项依次进行判断即可解答.
解答: 解:A、中的带分数要写成假分数;
B、中的2应写在字母的前面;
C、应写成分数的形式;
D、符合书写要求.
故选D.
点评: 本题主要考查代数式的书写要求:
(1)在代数式中出现的乘号,通常简写成“ ”或者省略不写;
(2)数字与字母相乘时,数字要写在字母的前面;
(3)在代数式中出现的除法运算,一般按照分数的写法来写.带分数要写成假分数的形式.
6.在2x2,1﹣2x=0,ab,a>0,0,,π中,是代数式的有( )
A. 5个 B. 4个 C. 3个 D. 2个
考点: 代数式.
分析: 代数式是有数和字母组成,表 ( http: / / www.21cnjy.com )示加、减、乘、除、乘方、开方等运算的式子,或含有字母的数学表达式,注意不能含有=、<、>、≤、≥、≈、≠等符号.
解答: 解:∵1﹣2x=0,a>0,含有=和>,所以不是代数式,
∴代数式的有2x2,ab,0,,π,共5个.
故选A.
点评: 此题主要考查了代数式的定义,掌握代数式的定义是本题的关键,注意含有=、<、>、≤、≥、≈、≠等符号的不是代数式.
7.通信市场竞争日益激烈,某通信公司的手机本 ( http: / / www.21cnjy.com )地话费标准按原标准每分钟降低a元后,再次下调了20%,现在收费标准是每分钟b元,则原收费标准每分钟是( )
A. (a+b)元 B. (a﹣b)元 C. (a+5b)元 D. (a﹣5b)元
考点: 列代数式.
专题: 压轴题.
分析: 首先表示出下调了20%后的价格,然后加上a元,即可得到.
解答: 解:b÷(1﹣20%)+a=a+b.
故选A.
点评: 本题考查了列代数式,正确理解题目中的关系是关键.
8.黄石市2011年6月份某日一天的温差为11℃,最高气温为t℃,则最低气温可表示为( )
A. (11+t)℃ B. (11﹣t)℃ C. (t﹣11)℃ D. (﹣t﹣11)℃
考点: 列代数式.
专题: 计算题.
分析: 由已知可知,最高气温﹣最低气温=温差,从而求出最低气温.
解答: 解:设最低气温为x℃,则:
t﹣x=11,
x=t﹣11.
故选C.
点评: 此题考查的知识点是列代数式,此题要明确温差就是最高气温减去最低气温.
9.某工厂第一年生产a件产品,第二年比第一年增产了20%,则两年共生产产品的件数为( )
A. 0.2a B. a C. 1.2a D. 2.2a
考点: 列代数式.
分析: 两年共生产产品的件数=第一年生产产品件数+第二年生产产品件数.
解答: 解:第二年生产产品件数为a×(1+20%)=1.2a,
∴两年共生产产品的件数为a+1.2a=2.2a,故选D.
点评: 解决问题的关键是读懂题意,找到所求的量的等量关系.注意应先求得第二年的生产的产品件数.
二.填空题(共10小题)
10.吉林广播电视塔“五一”假期第一天接待游客m人,第二天接待游客n人,则这2天平均每天接待游客 人(用含m、n的代数式表示).
考点: 列代数式.
分析: 用两天接待的游客总人数除以天数,即可得解.
解答: 解:2天平均每天接待游客.
故答案为:.
点评: 本题考查了列代数式,比较简单,熟练掌握平均数的求法是解题的关键.
11.学校购买了一批图书,共a箱,每箱有b册,将这批图书的一半捐给社区,则捐给社区的图书为 册(用含a、b的代数式表示).
考点: 列代数式.
分析: 首先根据题意可得这批图书共有ab册,它的一半就是册.
解答: 解:由题意得:这批图书共有ab册,
则图书的一半是:册.
故答案为:.
点评: 此题主要考查了列代数式,关键是弄清题目的意思,表示出这批图书的总数量,注意代数式的书写方法,除法要写成分数形式.
12.体育委员带了500元 ( http: / / www.21cnjy.com )钱去买体育用品,已知一个足球a元,一个篮球b元.则代数式500﹣3a﹣2b表示的数为 体育委员买了3个足球,2个篮球,剩余的经费 .
考点: 代数式.
专题: 应用题.
分析: 本题需先根据买一个足球a元,一个篮球b元的条件,表示出3a和2b的意义,最后得出正确答案即可.
解答: 解:∵买一个足球a元,一个篮球b元.
∴3a表示委员买了3个足球
2b表示买了2个篮球
∴代数式500﹣3a﹣2b:表示委员买了3个足球、2个篮球,剩余的经费.
故答案为:体育委员买了3个足球、2个篮球,剩余的经费
点评: 本题主要考查了列代数式,在解题时要根据题意表示出各项的意义是本题的关键.
13.实验中学初三年级12个班中共有团员a人,则表示的实际意义是 平均每班团员数 .
考点: 代数式.
专题: 压轴题.
分析: 总人数÷班级的个数=平均每班团员数.
解答: 解:表示的实际意义是平均每班团员数.
点评: 注意掌握代数式的实际意义.
14.代数式4a可表示的 ( http: / / www.21cnjy.com )实际意义是 答案不唯一,要求:符合代数式的意义,如:每去钢笔4元,买了a支钢笔所需的钱数,或正方形的边长为a,它的周长是4a.
考点: 代数式.
专题: 开放型.
分析: 根据代数式表示的意义和实际的联系编写场景即可.
解答: 解:答案不唯一.
如:每去钢笔4元,买了a支钢笔所需的钱数,
或正方形的边长为a,它的周长是4a.
点评: 此题综合考查代数式表示的意义和实际的联系.
15.若x2﹣2x=3,则代数式2x2﹣4x+3的值为 9 .
考点: 代数式求值.
专题: 计算题.
分析: 所求式子前两项提取2变形后,将已知等式代入计算即可求出值.
解答: 解:∵x2﹣2x=3,
∴2x2﹣4x+3=2(x2﹣2x)+3=6+3=9.
故答案为:9
点评: 此题考查了代数式求值,利用了整体代入的思想,是一道基本题型.
16.若x=﹣1,则代数式x3﹣x2+4的值为 2 .
考点: 代数式求值.
专题: 计算题.
分析: 把x=﹣1代入代数式进行计算即可得解.
解答: 解:x3﹣x2+4,
=(﹣1)3﹣(﹣1)2+4,
=﹣1﹣1+4,
=﹣2+4,
=2.
故答案为:2.
点评: 本题考查了代数式求值,把x的值代入进行计算即可得解,比较简单.
17.小明t小时走了s千米的路,则他走这段路的平均速度是 千米/时.
考点: 代数式.
分析: 根据速度的计算公式即可求得小明的平均速度.
解答: 解:小明走这段路的平均速度是千米/时.
点评: 本题考查了平均速度的计算.平均速度=总路程÷总时间.
18.今年五月份,由于H7N9禽流感的 ( http: / / www.21cnjy.com )影响,我市鸡肉的价格下降了10%,设鸡肉原来的价格为a元/千克,则五月份的价格为 0.9a 元/千克.
考点: 列代数式.
分析: 因为原来鸡肉价格为a元/千克,现在下降了10%,所以现在的价格为(1﹣10%)a,即0.9a元/千克.
解答: 解:∵原来鸡肉价格为a元/千克,现在下降了10%,
∴五月份的价格为a﹣10%a=(1﹣10%)a=0.9a,
故答案为:0.9a.
点评: 本题考查了列代数式的知识,解决 ( http: / / www.21cnjy.com )问题的关键是读懂题意,找到所求的量的等量关系.注意价格下降了10%就是指原来的价格减去原来价格的10%.
29.对单项式“5x”,我们可以这 ( http: / / www.21cnjy.com )样理解:香蕉每千克5元,某人买了x千克,共付款“5x”元.请你结合生活实际,再给出“5x”的另一个合理解释为: 某人的行走速度是x米/分,5分钟行走的路程. .
考点: 代数式.
专题: 开放型.
分析: 解释合理即可,答案不唯一.
解答: 解:对单项式“5x”,我们可以这样理解:某人的行走速度是x米/分,5分钟行走的路程.
点评: 此类问题应结合实际,根据代数式的特点解答.
三.解答题(共9小题)
20.下列各式哪些是代数式?哪些不是代数式?
(1)3>2;(2)a+b=5;(3)a;(4)3;(5)5+4﹣1;(6)m米;(7)5x﹣3y
考点: 代数式.
分析: 根据代数式的概念,用运算符号把数字与字母连接而成的式子叫做代数式.单独的一个数或一个字母也是代数式.
解答: 解:(1)、(2)中的“>”、“=”它们不是运算符号,因此(1)、(2)不是代数式.
(3)、(4)中a、3是代数式,因为单个数字和字母是代数式.
(5)中是加减运算符号把5、4、1连接起来,因此是代数式.
(6)m米含有单位名称,故不是代数式.
(7)5x﹣3y中由乘、减两种运算联起5、x、3、y,因此是代数式.
答:代数式有(3)(4)(5)(7);(1)(2)(6)不是代数式.
点评: 注意掌握代数式的定义.
21.说出下列代数式的意义:
(1)2(a+3);
(2)a2+b2;
(3).
考点: 代数式.
专题: 开放型.
分析: 说出下列代数式的意义,实际上就是把代数式用语言叙述出来.叙述时,要求既要表明运算的顺序,又要说出运算的最终结果.
解答: 解:(1)2(a+3)的意义是2与(a+3)的积;
(2)a2+b2的意义是a,b的平方的和;
(3)的意义是(n+1)除以(n﹣1)的商.
点评: 用语言表达代数式的意义,一定要理清代数式中含有的各种运算及其顺序.具体说法没有统一规定,以简明而不引起误会为出发点.
22.用字母表示图中阴影部分的面积.
( http: / / www.21cnjy.com )
考点: 代数式.
分析: (1)读图可得,阴影部分的面积=大长方形的面积﹣小长方形的面积;
(2)阴影部分的面积=正方形的面积﹣扇形的面积.
解答: 解:(1)阴影部分的面积=ab﹣bx;
(2)阴影部分的面积=R2﹣πR2.
点评: 解决问题的关键是读懂图,找到所求的阴影部分的面积和各部分之间的等量关系.
23.下面的两种移动电话计费方式表,考虑下列问题.
方式一 方式二
月租费 50元/月 10元/月
本地通话费 0.30元/分 0.5元/分
(1)一个月本地通话时间150分,计算按两种移动电话计费方式各需要交费多少元?
(2)你如何选择计费方式?为什么?(分类讨论)
考点: 有理数的混合运算;列代数式.
分析: (1)首先根据题意,计算出本地通话总计费,然后再加上月租费,即可推出两种激动电话计费各需要交费多少;
(2)要看我的电话一个月内的本地通话时间为多少分钟,首先设出通话时间为x,列出方程0.3x+50=0.5x+10,求出x,再进行分析即可.
解答: 解:(1)方式一:150×0.30+50=45+50=95(元),
方式二:150×0.5+10=75+10=85(元),
答:按方式一的计费方式需要交费95元,按方式二的计费方式需要交费85元,
(2)设一个月内本地通话x分钟时,两种通讯方式的费用相同,
∴0.3x+50=0.5x+10,
整理方程得:0.2x=40,
∴x=200.
∴若x<200分钟时,0.30x+50>0.5x+10,
若x>200分钟时,0.3x+50<0.5x+10,
答:若一个月内的电话时间多于200分钟,就选择计费方式一,
若一个月内的电话时间少于200分钟,就选择计费方式二,
若一个月内的电话时间等于200分钟,两种计费方式都可以选择.
点评: 本题主要考查有理数的混合运算,关键是求出两种通讯方式的费用相同时,一个月内的本地通话是多少分钟,找到此临界点.
24.某镇有A、B两家纯净水销售站,它们 ( http: / / www.21cnjy.com )所提供的纯净水的价格、质量都相同.为了促销,A站的纯净水每桶降价20%销售;B站规定:每个用户购买B站的纯净水,第1桶按照原价销售,若用户继续购买,则从第2桶开始每桶降价25%销售,促销活动都是三个月.若小明家预计三个月要购买12桶纯净水,请你帮他判断购买哪家的纯净水较省钱,并说明理由.
考点: 列代数式.
专题: 应用题;方案型.
分析: 缺少原价,可设原单价为a,那 ( http: / / www.21cnjy.com )么去A销售站需付费:原总价×(1﹣20%);在B站需花费的金额为:一桶原价+其余的原总价×(1﹣25%),然后进行比较.
解答: 解:设每桶纯净水的原价为a元,则购买12桶纯净水,
在A站需花费的金额为(1﹣20%)a 12=9.6a(元);
在B站需花费的金额为a+(1﹣25%)a 11=9.25a(元);
∵9.6a>9.25a,
∴小明家应选择到B家纯净水销售站购买纯净水,这样较省钱.
点评: 解决问题的关键是读懂题意,找到 ( http: / / www.21cnjy.com )所求的量的等量关系.要注意其中的关系:原总价×(1﹣20%);一桶原价+其余的原总价×(1﹣25%).
25.如果某三角形第一条边长为 ( http: / / www.21cnjy.com )(2a﹣b)cm,第二条边比第一条边长(a+b)cm,第三条边比第一条边的2倍少b(cm),求这个三角形的周长(用a、b的代数式表示).
考点: 列代数式.
专题: 应用题.
分析: 第二条边长为(2a﹣b)+(a+b),第三条边长为2(2a﹣b)﹣b,然后求三边的和即可.
解答: 解:周长=(2a﹣b)+[(2a﹣b)+(a+b)]+[2(2a﹣b)﹣b]
=2a﹣b+2a﹣b+a+b+4a﹣2b﹣b
=9a﹣4b.
点评: 解决问题的关键是读懂题意,找到所求的量的等量关系.本题只需仔细分析题意,进行多项式的加法运算即可.
26.某市电话拨号上网有两种收费方式,用户可以任选其一:
(A)计时制:0.05元每分钟;
(B)包月制:60元每月(限一部个人住宅电话上网);
此外,每一种上网方式都得加收通信费0.02元每分钟.
(1)某用户某月上网的时间为x小时,请分别写出两种收费方式下该用户应该支付的费用;
(2)若某用户估计一个月内上网的时间为25小时,你认为采用哪种方式较为合算?
考点: 列代数式.
分析: (1)首先统一时间单位,(A) ( http: / / www.21cnjy.com )计时制:每分钟(0.05+0.02)元×时间=花费;(B)包月制:60元+每分钟0.02元×时间=花费;
(2)把x=25代入(1)中的代数式计算出花费,进行比较即可.
解答: 解:(1)x小时=60x分钟,
(A)计时制:(0.05+0.02) 60x=0.07 60x=4.2x,
(B)包月制:60+0.02 60x=60+1.2x.
(2)A)计时制:4.2x=4.2×25=105(元),
(B)包月制:60+1.2x=60+1.2×25=90(元).
∵90<105,
∴用(B)方式较为合算.
点评: 此题主要考查了列代数式,并比较哪种花费便宜的问题,关键是弄清题意列出式子.
27.问题探究.
用如图所示正方形纸板制作一个无盖的长方体盒子,可在正方体的四角减去相同的正方形,剩余部分即可做成一个无盖的长方体形盒子.
(1)设正方形纸的边长为a,减去的小正方形的边长为x,请用a与x表示这个无盖长方体形盒子的容积;
(2)把正方形的纸板换成长为a,宽为b的长方形纸板,怎样做一个无盖长方体形盒子?画图说明你的做法;
(3)把(2)中做的长方体形盒子的容积用代数式表示出来;
(4)比较(1)和(3)的结果,说说它们的区别和联系.
( http: / / www.21cnjy.com )
考点: 列代数式.
分析: (1)观察图形可知底面长、宽都为(a﹣2x),高为x,用长方体的体积公式表示体积;
(2)在长方形纸板的四个角减去相同的正方形,剩余部分即可做成一个无盖的长方体形盒子;
(3)先设减去的正方形边长为x,然后求出长方体盒子的底面积,再乘以高即可得出答案;
(4)根据长方体和正方体的体积公式即可得出它们之间的区别和联系.
解答: 解:(1)依题意,长方体盒子容积为:(a﹣2x)2 x;
(2)画图如下:
( http: / / www.21cnjy.com )
(3)设减去的正方形边长为x,根据题意得:
(a﹣2x)(b﹣2x) x;
(4)(1)中底面积为正方形面积为(a﹣2 ( http: / / www.21cnjy.com )x)2,(3)中底面积为长方形,面积为(a﹣2x)(b﹣2x),高都为x,(3)中当a=b时即得到(1)中的结果.
点评: 此题考查了列代数式;本题关键是表示长方体的长、宽、高,再用体积公式计算.
28.小明将连续的奇数1,3,5,7,9,…,排成如图所示的数阵,用一个矩形框框住其中的9个数,如图所示.
(1)矩形阴影框中的9个数的和与中间一个数存在怎样的关系?(直接写出笞案)
(2)若将矩形框上下左右移动,这个关系还成立吗?为什么?
( http: / / www.21cnjy.com )
考点: 列代数式.
专题: 规律型.
分析: (1)将方框内的数字相加等于171,通过计算得出存在的关系.
(2)若将矩形框上下左右移动,可举两个实例证明是否成立.
解答: 解:(1)计算阴影框中9个数的和为,3+5+7+17+19+21+31+33+35=171,171÷19=9,
所以,矩形阴影框中的9个数的和是中间一个数的9倍;
(2)假设将矩形框向下移动一个格,则中间的数为33.
则9个数的和为,17+19+21+31+32+33+35+45+47+49=297,297÷33=9,
再假设将矩形框向左移动一个格,则中间的数为17,
则9个数的和为:1+3+5+15+17+19+29+31+33=153,153÷17=9.
所以这个关系还成立.
点评: 此题是通过计算得出存在的关系的,也可以通过观察总结出一定的规律进行解答.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
