2023-2024学年高中数学人教A版(2019)选择性必修第一册课后习题 第一章 1-3 空间向量及其运算的坐标表示(含解析)
文档属性
| 名称 | 2023-2024学年高中数学人教A版(2019)选择性必修第一册课后习题 第一章 1-3 空间向量及其运算的坐标表示(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 308.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-28 17:11:29 | ||
图片预览



文档简介
1.3 空间向量及其运算的坐标表示
A级 必备知识基础练
1.在空间直角坐标系Oxyz中,点A(1,-2,0)和向量a=(-3,4,12),且=2a,则点B的坐标为( )
A.(-7,10,24) B.(7,-10,-24)
C.(-6,8,24) D.(-5,6,24)
2.(多选题)下列各组两个向量中,平行的有( )
A.a=(1,-2,3),b=(1,2,1)
B.a=(0,-3,3),b=(0,1,-1)
C.a=(0,-3,2),b=0,1,-
D.a=1,-,3,b=(-2,1,-6)
3.已知点A(2,-5,1),B(2,-2,4),C(1,-4,1),则向量的夹角为( )
A.30° B.45° C.60° D.90°
4.若向量a=(1,-1,2),b=(2,1,-3),则|a+b|=( )
A. B.2 C.3 D.
5. 如图,在正方体ABCD -A1B1C1D1中,M,N分别是BC1,CD1的中点,则下列说法错误的是( )
A.MN与CC1垂直
B.MN与AC垂直
C.MN与BD平行
D.MN与A1B1平行
6.已知向量a=(1,1,x),b=(1,2,1),c=(1,1,1),若(c+a)·2b=-2,则实数x= .
7.已知向量a=(x,4,1),b=(-2,y,-1),c=(3,-2,z),a∥b,b⊥c,求:(1)a,b,c;(2)a+c与b+c所成角的余弦值.
8.如图所示,在正四棱锥P-ABCD中,底面ABCD是边长为1的正方形,O是AC与BD的交点,PO=1,M是PC的中点.设=a,=b,=c.
(1)用向量a,b,c表示;
(2)在如图所示的空间直角坐标系中,求的坐标.
B级 关键能力提升练
9.已知空间向量=(x,y,8),=(z,3,4),,且||=5,则实数z的值为 ( )
A.5 B.-5
C.5或-5 D.-10或10
10.已知O为坐标原点,=(1,2,3),=(2,1,2),=(1,1,2),点Q在直线OP上运动,则取得最小值时,点Q的坐标为 ( )
A.
B.
C.
D.
11.(多选题)从点P(1,2,3)出发,沿着向量v=(-4,-1,8)方向取点Q,使|PQ|=18,则Q点的坐标为( )
A.(-1,-2,3) B.(9,4,-13)
C.(-7,0,19) D.(1,-2,-3)
12.(多选题)正方体A1B1C1D1-ABCD的棱长为2,M为B1C1的中点,则下列说法正确的是 ( )
A.AB1与BC1成60°角
B.若,面A1MN交CD于点E,则CE=
C.点P在正方形ABB1A1边界及内部运动,且MP⊥DB1,则点P的轨迹长等于
D.E,F分别在棱DB1,A1C1上,且=2,直线EF与AD1,A1D所成角分别是α,β,则α+β=
13.已知点M(1,2,3),N(2,3,4),P(-1,2,-3),若||=3||,且,则的坐标为 ,点Q的坐标为 .
14.如图,将边长为1的正方形AA1O1O(及其内部)绕OO1旋转一周形成圆柱,的长为的长为,其中B1与C在平面AA1O1O的同侧.则异面直线B1C与AA1所成的角的大小为 .
15.已知空间三点A(0,2,3),B(-2,1,6),C(1,-1,5).
(1)求以AB和AC为邻边的平行四边形的面积;
(2)若|a|=,且a分别与垂直,求向量a的坐标.
C级 学科素养创新练
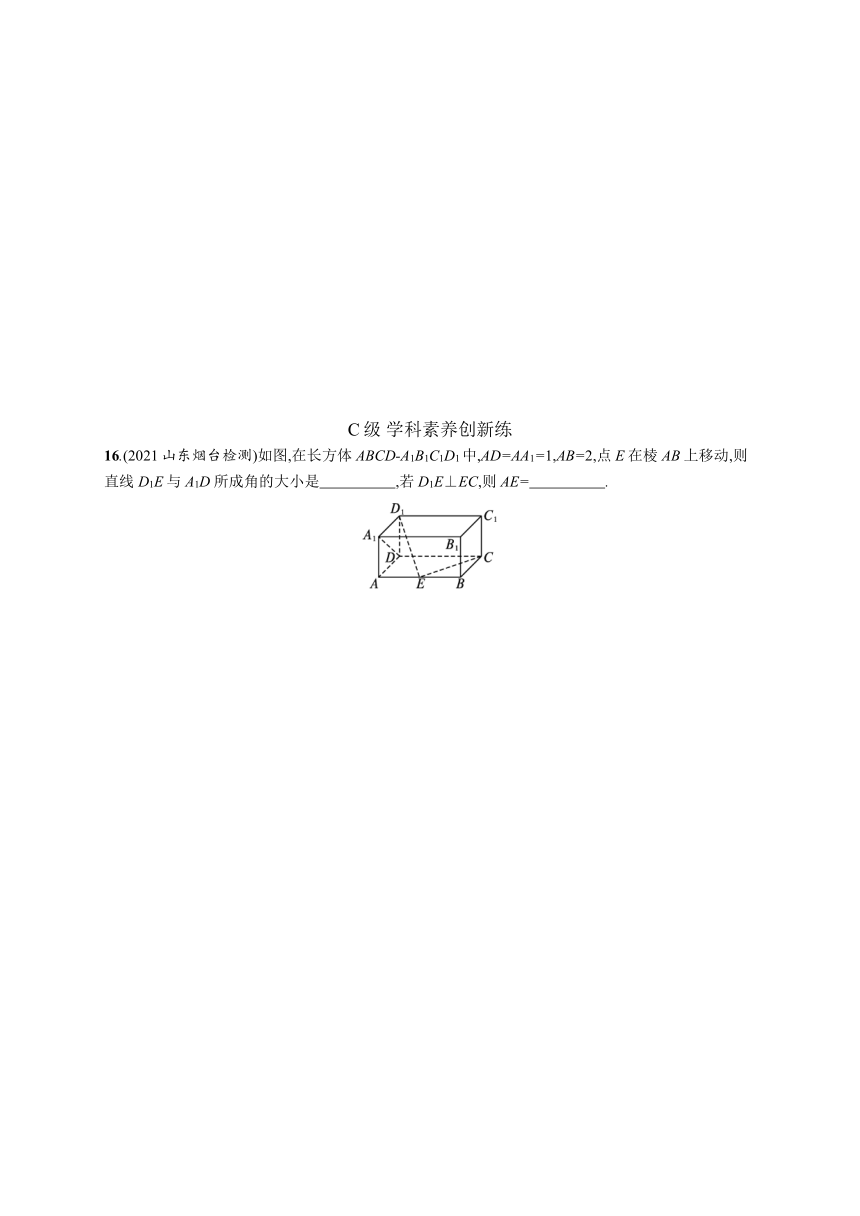
16.(2021山东烟台检测)如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动,则直线D1E与A1D所成角的大小是 ,若D1E⊥EC,则AE= .
1.3 空间向量及其运算的坐标表示
1.D ∵a=(-3,4,12),且=2a,∴=(-6,8,24).
∵A(1,-2,0),∴B(-5,6,24),故选D.
2.BD 对于B,有a=-3b,故a∥b;对于D,有b=-2a,故a∥b;而对A,C中两向量,不存在实数λ,使a=λb,故不平行.
3.C 由已知得=(0,3,3),=(-1,1,0),
因此cos<>=,
所以向量的夹角为60°.
4.D ∵a=(1,-1,2),b=(2,1,-3),
∴a+b=(3,0,-1),
∴|a+b|=.故选D.
5. D 设正方体的棱长为1,如图,建立空间直角坐标系,则A(1,0,0),B(1,1,0),C(0,1,0),D(0,0,0),A1(1,0,1),B1(1,1,1),C1(0,1,1),M,1,,N0,,
∴=-,-,0,=(0,0,1),
=(-1,1,0),=(-1,-1,0),=(0,1,0).
=0,∴MN⊥CC1,故A正确;=0,∴MN⊥AC,故B正确;易知=2,且M,N BD,
∴MN∥BD,故C正确;设=λ,得无解,∴MN与A1B1不平行,故D错误.
故选D.
6.-8 由已知得c+a=(2,2,x+1),2b=(2,4,2),
所以4+8+2(x+1)=-2,解得x=-8.
7.解(1)因为a∥b,所以,解得x=2,y=-4,这时a=(2,4,1),b=(-2,-4,-1).
又因为b⊥c,所以b·c=0,即-6+8-z=0,
解得z=2,所以c=(3,-2,2).
(2)由(1)得a+c=(5,2,3),b+c=(1,-6,1),
所以a+c与b+c所成角θ的余弦值cos θ==-.
8.解(1)∵,
∴)=)=-=-a+b+c.
(2)a==(1,0,0),b==(0,1,0).
∵A(0,0,0),O,0,P,1,
∴c==,1,
∴=-a+b+c=-×(1,0,0)+×(0,1,0)+×,1=-.
9.C 因为,所以存在λ∈R,使得=λ,
又||=5,而=(z-x,3-y,-4),
则
解得故选C.
10.C 点Q在直线OP上运动,设=λ=(λ,λ,2λ)(λ∈R),则=(1-λ,2-λ,3-2λ),=(2-λ,1-λ,2-2λ),
∴=6λ-2-,当λ=时,取得最小值,此时,Q.故选C.
11.BC 设Q(x0,y0,z0),则=λv,
即(x0-1,y0-2,z0-3)=λ(-4,-1,8).
由|PQ|=18,得=18,
所以λ=±2,
所以(x0-1,y0-2,z0-3)=±2(-4,-1,8),
所以故选BC.
12.ACD 如图,建立空间直角坐标系,则A(2,0,2),B(2,2,2),C(0,2,2),D(0,0,2),A1(2,0,0),B1(2,2,0),C1(0,2,0),D1(0,0,0),M(1,2,0).
对于A,=(0,2,-2),=(-2,0,-2),
cos<>=,
∴AB1与BC1成60°角,故A正确;
对于B,∵,
∴N0,2,,设E(0,m,2),则=(-1,2,0),=-2,2,,=(-2,m,2),由已知得A1,M,N,E四点共面,∴ λ,μ∈R,使得=λ+μ,
得
解得
∴E0,,2,∴=0,-,0,||=,故B错误;
对于C,设P(2,y,z)(0≤y≤2,0≤z≤2),则=(1,y-2,z),=(2,2,-2),
由=2+2y-4-2z=0,得y-z=1,
∴点P的轨迹长为线段y-z=1(1≤y≤2)的长度,为,故C正确;
对于D,∵E,F分别在DB1,A1C1上,且=2,
∴×(2,2,-2)=,-,×(-2,2,0)=-,0,
则E,F,0,则=-,0,-,则cos α=|cos<>|
===1,
故α=0,
cos β=|cos<>|
==0,
故β=,即α+β=,故D正确.故选ACD.
13.(1,1,1) (-4,-1,-6)或(2,5,0) 由已知得=(1,1,1),设Q(x,y,z),
则=(x+1,y-2,z+3),由题意,得
解得
故点Q的坐标为(-4,-1,-6)或(2,5,0).
14. 以O为坐标原点,OA,OO1所在直线分别为y轴、z轴建立如图所示的空间直角坐标系Oxyz,
则A(0,1,0),A1(0,1,1),B1,1,C,-,0.
所以=(0,0,1),=(0,-1,-1),
则=02+0×(-1)+1×(-1)=-1,
所以cos<>==-.
因此,异面直线B1C与AA1所成的角为.
15.解(1)由题中条件可知,=(-2,-1,3),=(1,-3,2),
所以cos<>=.
于是sin<>=.
故以AB和AC为邻边的平行四边形的面积为
S=||||sin<>=14×=7.
(2)设a=(x,y,z),由题意得
解得
故a=(1,1,1)或a=(-1,-1,-1).
16.90° 1 在长方体ABCD-A1B1C1D1中,以D为原点,建立如图所示的空间直角坐标系.
又AD=AA1=1,AB=2,点E在棱AB上移动.
则D(0,0,0),D1(0,0,1),A(1,0,0),A1(1,0,1),C(0,2,0).
设E(1,m,0),0≤m≤2,
则=(1,m,-1),=(-1,0,-1),
∴=-1+0+1=0,
∴直线D1E与A1D所成角的大小是90°.
∵=(1,m,-1),=(-1,2-m,0),D1E⊥EC,
∴=-1+m(2-m)+0=0,
A级 必备知识基础练
1.在空间直角坐标系Oxyz中,点A(1,-2,0)和向量a=(-3,4,12),且=2a,则点B的坐标为( )
A.(-7,10,24) B.(7,-10,-24)
C.(-6,8,24) D.(-5,6,24)
2.(多选题)下列各组两个向量中,平行的有( )
A.a=(1,-2,3),b=(1,2,1)
B.a=(0,-3,3),b=(0,1,-1)
C.a=(0,-3,2),b=0,1,-
D.a=1,-,3,b=(-2,1,-6)
3.已知点A(2,-5,1),B(2,-2,4),C(1,-4,1),则向量的夹角为( )
A.30° B.45° C.60° D.90°
4.若向量a=(1,-1,2),b=(2,1,-3),则|a+b|=( )
A. B.2 C.3 D.
5. 如图,在正方体ABCD -A1B1C1D1中,M,N分别是BC1,CD1的中点,则下列说法错误的是( )
A.MN与CC1垂直
B.MN与AC垂直
C.MN与BD平行
D.MN与A1B1平行
6.已知向量a=(1,1,x),b=(1,2,1),c=(1,1,1),若(c+a)·2b=-2,则实数x= .
7.已知向量a=(x,4,1),b=(-2,y,-1),c=(3,-2,z),a∥b,b⊥c,求:(1)a,b,c;(2)a+c与b+c所成角的余弦值.
8.如图所示,在正四棱锥P-ABCD中,底面ABCD是边长为1的正方形,O是AC与BD的交点,PO=1,M是PC的中点.设=a,=b,=c.
(1)用向量a,b,c表示;
(2)在如图所示的空间直角坐标系中,求的坐标.
B级 关键能力提升练
9.已知空间向量=(x,y,8),=(z,3,4),,且||=5,则实数z的值为 ( )
A.5 B.-5
C.5或-5 D.-10或10
10.已知O为坐标原点,=(1,2,3),=(2,1,2),=(1,1,2),点Q在直线OP上运动,则取得最小值时,点Q的坐标为 ( )
A.
B.
C.
D.
11.(多选题)从点P(1,2,3)出发,沿着向量v=(-4,-1,8)方向取点Q,使|PQ|=18,则Q点的坐标为( )
A.(-1,-2,3) B.(9,4,-13)
C.(-7,0,19) D.(1,-2,-3)
12.(多选题)正方体A1B1C1D1-ABCD的棱长为2,M为B1C1的中点,则下列说法正确的是 ( )
A.AB1与BC1成60°角
B.若,面A1MN交CD于点E,则CE=
C.点P在正方形ABB1A1边界及内部运动,且MP⊥DB1,则点P的轨迹长等于
D.E,F分别在棱DB1,A1C1上,且=2,直线EF与AD1,A1D所成角分别是α,β,则α+β=
13.已知点M(1,2,3),N(2,3,4),P(-1,2,-3),若||=3||,且,则的坐标为 ,点Q的坐标为 .
14.如图,将边长为1的正方形AA1O1O(及其内部)绕OO1旋转一周形成圆柱,的长为的长为,其中B1与C在平面AA1O1O的同侧.则异面直线B1C与AA1所成的角的大小为 .
15.已知空间三点A(0,2,3),B(-2,1,6),C(1,-1,5).
(1)求以AB和AC为邻边的平行四边形的面积;
(2)若|a|=,且a分别与垂直,求向量a的坐标.
C级 学科素养创新练
16.(2021山东烟台检测)如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动,则直线D1E与A1D所成角的大小是 ,若D1E⊥EC,则AE= .
1.3 空间向量及其运算的坐标表示
1.D ∵a=(-3,4,12),且=2a,∴=(-6,8,24).
∵A(1,-2,0),∴B(-5,6,24),故选D.
2.BD 对于B,有a=-3b,故a∥b;对于D,有b=-2a,故a∥b;而对A,C中两向量,不存在实数λ,使a=λb,故不平行.
3.C 由已知得=(0,3,3),=(-1,1,0),
因此cos<>=,
所以向量的夹角为60°.
4.D ∵a=(1,-1,2),b=(2,1,-3),
∴a+b=(3,0,-1),
∴|a+b|=.故选D.
5. D 设正方体的棱长为1,如图,建立空间直角坐标系,则A(1,0,0),B(1,1,0),C(0,1,0),D(0,0,0),A1(1,0,1),B1(1,1,1),C1(0,1,1),M,1,,N0,,
∴=-,-,0,=(0,0,1),
=(-1,1,0),=(-1,-1,0),=(0,1,0).
=0,∴MN⊥CC1,故A正确;=0,∴MN⊥AC,故B正确;易知=2,且M,N BD,
∴MN∥BD,故C正确;设=λ,得无解,∴MN与A1B1不平行,故D错误.
故选D.
6.-8 由已知得c+a=(2,2,x+1),2b=(2,4,2),
所以4+8+2(x+1)=-2,解得x=-8.
7.解(1)因为a∥b,所以,解得x=2,y=-4,这时a=(2,4,1),b=(-2,-4,-1).
又因为b⊥c,所以b·c=0,即-6+8-z=0,
解得z=2,所以c=(3,-2,2).
(2)由(1)得a+c=(5,2,3),b+c=(1,-6,1),
所以a+c与b+c所成角θ的余弦值cos θ==-.
8.解(1)∵,
∴)=)=-=-a+b+c.
(2)a==(1,0,0),b==(0,1,0).
∵A(0,0,0),O,0,P,1,
∴c==,1,
∴=-a+b+c=-×(1,0,0)+×(0,1,0)+×,1=-.
9.C 因为,所以存在λ∈R,使得=λ,
又||=5,而=(z-x,3-y,-4),
则
解得故选C.
10.C 点Q在直线OP上运动,设=λ=(λ,λ,2λ)(λ∈R),则=(1-λ,2-λ,3-2λ),=(2-λ,1-λ,2-2λ),
∴=6λ-2-,当λ=时,取得最小值,此时,Q.故选C.
11.BC 设Q(x0,y0,z0),则=λv,
即(x0-1,y0-2,z0-3)=λ(-4,-1,8).
由|PQ|=18,得=18,
所以λ=±2,
所以(x0-1,y0-2,z0-3)=±2(-4,-1,8),
所以故选BC.
12.ACD 如图,建立空间直角坐标系,则A(2,0,2),B(2,2,2),C(0,2,2),D(0,0,2),A1(2,0,0),B1(2,2,0),C1(0,2,0),D1(0,0,0),M(1,2,0).
对于A,=(0,2,-2),=(-2,0,-2),
cos<>=,
∴AB1与BC1成60°角,故A正确;
对于B,∵,
∴N0,2,,设E(0,m,2),则=(-1,2,0),=-2,2,,=(-2,m,2),由已知得A1,M,N,E四点共面,∴ λ,μ∈R,使得=λ+μ,
得
解得
∴E0,,2,∴=0,-,0,||=,故B错误;
对于C,设P(2,y,z)(0≤y≤2,0≤z≤2),则=(1,y-2,z),=(2,2,-2),
由=2+2y-4-2z=0,得y-z=1,
∴点P的轨迹长为线段y-z=1(1≤y≤2)的长度,为,故C正确;
对于D,∵E,F分别在DB1,A1C1上,且=2,
∴×(2,2,-2)=,-,×(-2,2,0)=-,0,
则E,F,0,则=-,0,-,则cos α=|cos<>|
===1,
故α=0,
cos β=|cos<>|
==0,
故β=,即α+β=,故D正确.故选ACD.
13.(1,1,1) (-4,-1,-6)或(2,5,0) 由已知得=(1,1,1),设Q(x,y,z),
则=(x+1,y-2,z+3),由题意,得
解得
故点Q的坐标为(-4,-1,-6)或(2,5,0).
14. 以O为坐标原点,OA,OO1所在直线分别为y轴、z轴建立如图所示的空间直角坐标系Oxyz,
则A(0,1,0),A1(0,1,1),B1,1,C,-,0.
所以=(0,0,1),=(0,-1,-1),
则=02+0×(-1)+1×(-1)=-1,
所以cos<>==-.
因此,异面直线B1C与AA1所成的角为.
15.解(1)由题中条件可知,=(-2,-1,3),=(1,-3,2),
所以cos<>=.
于是sin<>=.
故以AB和AC为邻边的平行四边形的面积为
S=||||sin<>=14×=7.
(2)设a=(x,y,z),由题意得
解得
故a=(1,1,1)或a=(-1,-1,-1).
16.90° 1 在长方体ABCD-A1B1C1D1中,以D为原点,建立如图所示的空间直角坐标系.
又AD=AA1=1,AB=2,点E在棱AB上移动.
则D(0,0,0),D1(0,0,1),A(1,0,0),A1(1,0,1),C(0,2,0).
设E(1,m,0),0≤m≤2,
则=(1,m,-1),=(-1,0,-1),
∴=-1+0+1=0,
∴直线D1E与A1D所成角的大小是90°.
∵=(1,m,-1),=(-1,2-m,0),D1E⊥EC,
∴=-1+m(2-m)+0=0,
