3.2代数式的值 跟踪训练(含详细解析)
文档属性
| 名称 | 3.2代数式的值 跟踪训练(含详细解析) |  | |
| 格式 | zip | ||
| 文件大小 | 57.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-24 14:52:20 | ||
图片预览




文档简介
i 第三章整式加减3.2代数式的值
农安县合隆镇 徐亚惠
一.选择题(共8小题)
1.按如图的运算程序,能使输出结果为3的x,y的值是( )
( http: / / www.21cnjy.com )h
A. x=5,y=﹣2 B.x=3,y=﹣3 C x=﹣4,y=2 D. x=﹣3,y=﹣9
2.已知x2﹣2x﹣3=0,则2x2﹣4x的值为( )
A. ﹣6 B.6 C.﹣2或6 D. ﹣2或30
3.当x=1时,代数式ax3﹣3bx+4的值是7,则当x=﹣1时,这个代数式的值是( )
A. 7 B.3 C 1 D. ﹣7
4.若m+n=﹣1,则(m+n)2﹣2m﹣2n的值是( )
A. 3 B.0 C.1 D. 2
5.若2a﹣b=3,则9﹣4a+2b的值为( )
A. 12 B.6 C.3 D. 0
6.a、b经过运算后得到的结果如下表所示:
a 0.5 0.25
b 2 4
运算结果 4 16
下列可以得到上述运算结果的算式是( )
A. ab﹣1 B.a﹣1b C.ab D. (ab)2
7.已知x2﹣2x﹣8=0,则3x2﹣6x﹣18的值为( )
A. 54 B. 6 C. ﹣10 D. ﹣18
8.当x=2时,代数式的值是( )
A. ﹣1 B.0 C.1 D. 1
二.填空题(共7小题)
9.若m+n=0,则2m+2n+1= _________ .
10.已知x(x+3)=1,则代数式2x2+6x﹣5的值为 _________ .
11.若m2﹣2m﹣1=0,则代数式2m2﹣4m+3的值为 _________ .
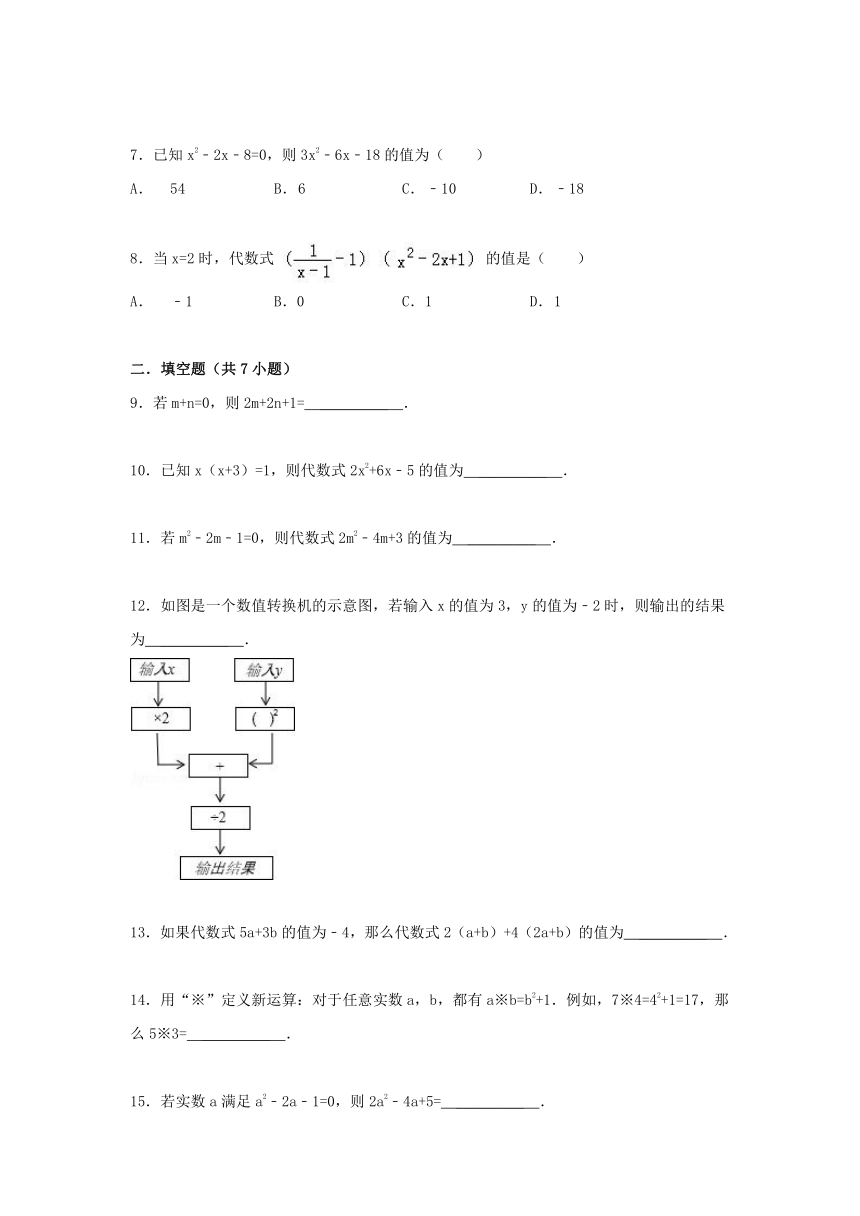
12.如图是一个数值转换机的示意图,若输入x的值为3,y的值为﹣2时,则输出的结果为 _________ .
( http: / / www.21cnjy.com )
13.如果代数式5a+3b的值为﹣4,那么代数式2(a+b)+4(2a+b)的值为 _________ .
14.用“※”定义新运算:对于任意实数a,b,都有a※b=b2+1.例如,7※4=42+1=17,那么5※3= _________ .
15.若实数a满足a2﹣2a﹣1=0,则2a2﹣4a+5= _________ .
三.解答题(共6小题)
16.已知当x=1时,2ax2+bx的值为﹣2,求当x=2时,ax2+bx的值.
17.已知:x2﹣5x=6,请你求出代数式10x﹣2x2+5的值.
18.已知代数式3x2﹣4x+6值为9,则x2﹣+6的值.
19.2008年6月1日北京奥运圣火在宜昌 ( http: / / www.21cnjy.com )传递,圣火传递路线分为两段,其中在市区的传递路程为700(a﹣1)米,三峡坝区的传递路程为(881a+2309)米.设圣火在宜昌的传递总路程为s米,
(1)用含a的代数式表示s;
(2)已知a=11,求s的值.
20.如图所示是一个数表,现用一个矩形在数表中任意框出4个数,则
(1)a、c的关系是: _________ ;
(2)当a+b+c+d=32时,a= _________ .
( http: / / www.21cnjy.com )
21.已知a、b互为相反数,c、d互为倒数,|d|=2,x2=4,求:
(1)2x12的值;
(2)(a+b)+﹣的值.
第三章整式加减3.2代数式的值
参考答案与试题解析
一.选择题(共8小题)
1.按如图的运算程序,能使输出结果为3的x,y的值是( )
( http: / / www.21cnjy.com )
A. x=5,y=﹣2 B.x=3,y=﹣3 C x=﹣4,y=2 D. x=﹣3,y=﹣9
考点:-代数式求值;二元一次方程的解.
专题:-计算题.
分析:-根据运算程序列出方程,再根据二元一次方程的解的定义对各选项分析判断利用排除法求解.
解答:-解:由题意得,2x﹣y=3,
A、x=5时,y=7,故A选项错误;
B、x=3时,y=3,故B选项错误;
C、x=﹣4时,y=﹣11,故C选项错误;
D、x=﹣3时,y=﹣9,故D选项正确.
故选:D.
点评:-本题考查了代数式求值,主要利用了二元一次方程的解,理解运算程序列出方程是解题的关键.
2.已知x2﹣2x﹣3=0,则2x2﹣4x的值为( )
A. ﹣6 B.6 C ﹣2或6 D. ﹣2或30
考点:-代数式求值.
专题:-整体思想.
分析:-方程两边同时乘以2,再化出2x2﹣4x求值.
解答:-解:x2﹣2x﹣3=0
2×(x2﹣2x﹣3)=0
2×(x2﹣2x)﹣6=0
2x2﹣4x=6
故选:B.
点评:-本题考查代数式求值,解题的关键是化出要求的2x2﹣4x.
3.当x=1时,代数式ax3﹣3bx+4的值是7,则当x=﹣1时,这个代数式的值是( )
A. 7 B.3 C 1 D. ﹣7
考点:-代数式求值.
专题:-整体思想.
分析:-把x=1代入代数式求出a、b的关系式,再把x=﹣1代入进行计算即可得解.
解答:-解:x=1时,ax3﹣3bx+4=a﹣3b+4=7,
解得a﹣3b=3,
当x=﹣1时,ax3﹣3bx+4=﹣a+3b+4=﹣3+4=1.
故选:C.
点评:-本题考查了代数式求值,整体思想的利用是解题的关键.
4.若m+n=﹣1,则(m+n)2﹣2m﹣2n的值是( )
A. 3 B.0 C 1 D. 2
考点:-代数式求值.
专题:-整体思想.
分析:-把(m+n)看作一个整体并代入所求代数式进行计算即可得解.
解答:-解:∵m+n=﹣1,
∴(m+n)2﹣2m﹣2n
=(m+n)2﹣2(m+n)
=(﹣1)2﹣2×(﹣1)
=1+2
=3.
故选:A.
点评:-本题考查了代数式求值,整体思想的利用是解题的关键.
5.若2a﹣b=3,则9﹣4a+2b的值为( )
A. 12 B.6 C.3 D. 0
考点:-代数式求值.
专题:-计算题.
分析:-所求式子后两项提取﹣2变形后,将2a﹣b的值代入计算即可求出值.
解答:-解:∵2a﹣b=3,
∴9﹣4a+2b=9﹣2(2a﹣b)=9﹣6=3.
故选C
点评:-此题考查了代数式求值,利用了整体代入的思想,将所求式子进行适当的变形是解本题的关键.
6.a、b经过运算后得到的结果如下表所示:
a 0.5 0.25
b 2 4
运算结果 4 16
下列可以得到上述运算结果的算式是( )
A. ab﹣1 B.a﹣1b C ab D. (ab)2
考点:-代数式求值;负整数指数幂.
分析:-根据表格数据,从负整数指数次幂等于正整数指数次幂的倒数考虑求解.
解答:-解:∵=4,=16,
∴表示运算结果的算式是a﹣1b.
故选B.
点评:-本题考查了代数式求值,从负整数指数幂考虑求解是解题的关键.
7.已知x2﹣2x﹣8=0,则3x2﹣6x﹣18的值为( )
A. 54 B.6 C ﹣10 D. ﹣18
考点:-代数式求值.
专题:-计算题.
分析:-所求式子前两项提取3变形后,将已知等式变形后代入计算即可求出值.
解答:-解:∵x2﹣2x﹣8=0,即x2﹣2x=8,
∴3x2﹣6x﹣18=3(x2﹣2x)﹣18=24﹣18=6.
故选B.
点评:-此题考查了代数式求值,利用了整体代入的思想,是一道基本题型.
8.当x=2时,代数式的值是( )
A. ﹣1 B.0 C 1 D. 1
考点:-代数式求值.
分析:-把x=2代入代数式进行计算即可得解.
解答:-解:x=2时,(﹣1)(x2﹣2x+1)=(﹣1)(12﹣2+1)=0.
故选B.
点评:-本题考查了代数式求值,是基础题,准确计算是解题的关键.
二.填空题(共7小题)
9.若m+n=0,则2m+2n+1= 1 .
考点:-代数式求值.
分析:-把所求代数式转化成已知条件的形式,然后整体代入进行计算即可得解.
解答:-解:∵m+n=0,
∴2m+2n+1=2(m+n)+1,
=2×0+1,
=0+1,
=1.
故答案为:1.
点评:-本题考查了代数式求值,整体思想的利用是解题的关键.
10.已知x(x+3)=1,则代数式2x2+6x﹣5的值为 ﹣3 .
考点:-代数式求值;单项式乘多项式.
专题:-整体思想.
分析:-把所求代数式整理出已知条件的形式,然后代入数据进行计算即可得解.
解答:-解:∵x(x+3)=1,
∴2x2+6x﹣5=2x(x+3)﹣5=2×1﹣5=2﹣5=﹣3.
s故答案为:﹣3.
点评:-本题考查了代数式求值,整体思想的利用是解题的关键.
11.若m2﹣2m﹣1=0,则代数式2m2﹣4m+3的值为 5 .
考点:-代数式求值.
专题:-整体思想.
分析:-先求出m2﹣2m的值,然后把所求代数式整理出已知条件的形式并代入进行计算即可得解.
解答:-解:由m2﹣2m﹣1=0得m2﹣2m=1,
所以,2m2﹣4m+3=2(m2﹣2m)+3=2×1+3=5.
故答案为:5.
点评:-本题考查了代数式求值,整体思想的利用是解题的关键.
12.如图是一个数值转换机的示意图,若输入x的值为3,y的值为﹣2时,则输出的结果为 5 .
( http: / / www.21cnjy.com )
考点:-代数式求值.
专题:-图表型.
分析:-把x=3,y=﹣2输入此程序即可.
解答:-解:把x=3,y=﹣2输入此程序得,
[3×2+(﹣2)2]÷2=10÷2=5.
点评:-解答本题的关键就是弄清楚题目给出的计算程序.
13.如果代数式5a+3b的值为﹣4,那么代数式2(a+b)+4(2a+b)的值为 ﹣8 .
考点:-代数式求值.
分析:-由于5a+3b的值为﹣4,故只需把要求的式子整理成含(5a+3b)的形式,代入求值即可.
解答:-解:∵5a+3b=﹣4,
∴原式=2a+2b+8a+4b=10a+6b=2(5a+3b)=2×(﹣4)=﹣8.
点评:-做此类题的时候,应先得到只含未知字母的代数式的值为多少,把要求的式子整理成包含那个代数式的形式.
b14.用“※”定义新运算:对于任意实数a,b,都有a※b=b2+1.例如,7※4=42+1=17,那么5※3= 10 .
考点:-代数式求值.
专题:-新定义.
分析:-熟悉新运算的计算规则,运用新规则计算.
解答:-解:依规则可知:5※3=32+1=10;
故答案为:10.
点评:-此题考查的知识点是代数式求值,关键是掌握新运算规则,然后再运用.
15.若实数a满足a2﹣2a﹣1=0,则2a2﹣4a+5= 7 .
考点:-代数式求值.
专题:-计算题.
分析:-根据a2﹣2a﹣1=0得出a2﹣2a=1,然后等式的左右两边同乘以2即可得到2a2﹣4a=2,再求2a2﹣4a+5的值就容易了.
解答:-解:∵a2﹣2a﹣1=0,
∴a2﹣2a=1,
∴2a2﹣4a=2,
∴2a2﹣4a+5=2+5=7.
故答案为7.
点评:-本题考查了代数式求值,解题的关键是求出2a2﹣4a的值,再代入2a2﹣4a+5即可.
三.解答题(共6小题)
16.已知当x=1时,2ax2+bx的值为﹣2,求当x=2时,ax2+bx的值.
考点:-代数式求值.
专题:-整体思想.
分析:-把x=1代入代数式求出a、b的关系式,再把x=2代入代数式整理即可得解.
解答:-解:将x=1代入2ax2+bx=﹣2中,
得2a+b=﹣2,
当x=2时,ax2+bx=4a+2b,
=2(2a+b),
=2×(﹣2),
=﹣4.
点评:-本题考查了代数式求值,整体思想的利用是解题的关键.
17.已知:x2﹣5x=6,请你求出代数式10x﹣2x2+5的值.
考点:-代数式求值.
专题:-整体思想.
分析:-先把10x﹣2x2+5变形为﹣2(x2﹣5x)+5,然后把x2﹣5x=6整体代入进行计算即可.
解答:-解:10x﹣2x2+5
=﹣2(x2﹣5x)+5,
∵x2﹣5x=6,
∴原式=﹣2×6+5=﹣12+5=﹣7.
点评:-本题考查了代数式求值:先根据已知条件把代数式进行变形,然后利用整体代入进行求值.
18.已知代数式3x2﹣4x+6值为9,则x2﹣+6的值.
考点:-代数式求值.
专题:-整体思想.
分析:-先根据题意列出等式3x2﹣4x+6=9,求得3x2﹣4x的值,然后求得x2﹣+6的值.
解答:-解:∵代数式3x2﹣4x+6值为9,∴3x2﹣4x+6=9,∴3x2﹣4x=3,
∴x2﹣=1,∴x2﹣+6=1+6=7.
点评:-本题考查了求代数式的值,找出未知与已知的关系,然后运用整体代入的思想.
19.2008年6月1日北京奥运圣火在宜昌 ( http: / / www.21cnjy.com )传递,圣火传递路线分为两段,其中在市区的传递路程为700(a﹣1)米,三峡坝区的传递路程为(881a+2309)米.设圣火在宜昌的传递总路程为s米,
(1)用含a的代数式表示s;
(2)已知a=11,求s的值.
考点:-代数式求值;列代数式.
专题:-计算题.
分析:-(1)中直接利用:总路程=市区的传递路程+三峡坝区的传递路程,代入相应的代数式,去括号,合并同类项,即可.
(2)已知a的值,求s,直接把a的值代入(1)中所得出的式子,即可求出s的值.
解答:-解:(1)s=700(a﹣1)+(881a+2309),
=1581a+1609;
(2)a=11时,
s=1581a+1609=1581×11+1609,
=19000.
点评:-此题的关键是找到题 ( http: / / www.21cnjy.com )目中给出的三个量的关系:总路程=市区的传递路程+三峡坝区的传递路程.然后把对应的数值或式子代入,根据要求解题即可.代数式求值问题是把字母的值直接代入相应的代数式即可.
20.如图所示是一个数表,现用一个矩形在数表中任意框出4个数,则
(1)a、c的关系是: a=c﹣5 ;
(2)当a+b+c+d=32时,a= 5 .
( http: / / www.21cnjy.com )
考点:-代数式求值;列代数式;一元一次方程的应用.
专题:-压轴题;图表型.
分析:-(1)结合图任意列举两组数字,即可发现a与c的关系;
(2)根据已知条件列一元一次方程求解即可.
解答:-解:(1)当a为4时,c=9,∴c﹣a=5,即a=c﹣5,
当a=9时,c=14,
∴c﹣a=5,即a=c﹣5,
∴a、c的关系是:a=c﹣5;
(2)设a=x,则b=x+1,c=x+5,d=x+6,
∵a+b+c+d=32,
∴x+x+1+x+5+x+6=32,
解得x=5,
∴a=5.
点评:-本题考查了代数式求值和一元一次方程的应用,解题的关键是结合图表弄清题意.
21.已知a、b互为相反数,c、d互为倒数,|d|=2,x2=4,求:
(1)2x12的值;
(2)(a+b)+﹣的值.
考点:-代数式求值;相反数;绝对值;倒数;有理数的乘方.
专题:-计算题.
分析:-(1)原式利用幂的乘方运算法则变形,将x2=4代入计算即可求出值;
(2)利用相反数,倒数的定义,平方根定义,以及绝对值的代数意义,求出a+b,cd,x的值,代入原式计算即可得到结果.
解答:-解:(1)∵x2=4,
∴2x12=2(x2)6=2×46=8192;
(2)根据题意得:a+b=0,cd=1,d=2或﹣2,x=2或﹣2,
则原式=0+2﹣0=2.
点评:-此题考查了代数式求值,以及非负数的性质,熟练掌握运算法则是解本题的关键.
农安县合隆镇 徐亚惠
一.选择题(共8小题)
1.按如图的运算程序,能使输出结果为3的x,y的值是( )
( http: / / www.21cnjy.com )h
A. x=5,y=﹣2 B.x=3,y=﹣3 C x=﹣4,y=2 D. x=﹣3,y=﹣9
2.已知x2﹣2x﹣3=0,则2x2﹣4x的值为( )
A. ﹣6 B.6 C.﹣2或6 D. ﹣2或30
3.当x=1时,代数式ax3﹣3bx+4的值是7,则当x=﹣1时,这个代数式的值是( )
A. 7 B.3 C 1 D. ﹣7
4.若m+n=﹣1,则(m+n)2﹣2m﹣2n的值是( )
A. 3 B.0 C.1 D. 2
5.若2a﹣b=3,则9﹣4a+2b的值为( )
A. 12 B.6 C.3 D. 0
6.a、b经过运算后得到的结果如下表所示:
a 0.5 0.25
b 2 4
运算结果 4 16
下列可以得到上述运算结果的算式是( )
A. ab﹣1 B.a﹣1b C.ab D. (ab)2
7.已知x2﹣2x﹣8=0,则3x2﹣6x﹣18的值为( )
A. 54 B. 6 C. ﹣10 D. ﹣18
8.当x=2时,代数式的值是( )
A. ﹣1 B.0 C.1 D. 1
二.填空题(共7小题)
9.若m+n=0,则2m+2n+1= _________ .
10.已知x(x+3)=1,则代数式2x2+6x﹣5的值为 _________ .
11.若m2﹣2m﹣1=0,则代数式2m2﹣4m+3的值为 _________ .
12.如图是一个数值转换机的示意图,若输入x的值为3,y的值为﹣2时,则输出的结果为 _________ .
( http: / / www.21cnjy.com )
13.如果代数式5a+3b的值为﹣4,那么代数式2(a+b)+4(2a+b)的值为 _________ .
14.用“※”定义新运算:对于任意实数a,b,都有a※b=b2+1.例如,7※4=42+1=17,那么5※3= _________ .
15.若实数a满足a2﹣2a﹣1=0,则2a2﹣4a+5= _________ .
三.解答题(共6小题)
16.已知当x=1时,2ax2+bx的值为﹣2,求当x=2时,ax2+bx的值.
17.已知:x2﹣5x=6,请你求出代数式10x﹣2x2+5的值.
18.已知代数式3x2﹣4x+6值为9,则x2﹣+6的值.
19.2008年6月1日北京奥运圣火在宜昌 ( http: / / www.21cnjy.com )传递,圣火传递路线分为两段,其中在市区的传递路程为700(a﹣1)米,三峡坝区的传递路程为(881a+2309)米.设圣火在宜昌的传递总路程为s米,
(1)用含a的代数式表示s;
(2)已知a=11,求s的值.
20.如图所示是一个数表,现用一个矩形在数表中任意框出4个数,则
(1)a、c的关系是: _________ ;
(2)当a+b+c+d=32时,a= _________ .
( http: / / www.21cnjy.com )
21.已知a、b互为相反数,c、d互为倒数,|d|=2,x2=4,求:
(1)2x12的值;
(2)(a+b)+﹣的值.
第三章整式加减3.2代数式的值
参考答案与试题解析
一.选择题(共8小题)
1.按如图的运算程序,能使输出结果为3的x,y的值是( )
( http: / / www.21cnjy.com )
A. x=5,y=﹣2 B.x=3,y=﹣3 C x=﹣4,y=2 D. x=﹣3,y=﹣9
考点:-代数式求值;二元一次方程的解.
专题:-计算题.
分析:-根据运算程序列出方程,再根据二元一次方程的解的定义对各选项分析判断利用排除法求解.
解答:-解:由题意得,2x﹣y=3,
A、x=5时,y=7,故A选项错误;
B、x=3时,y=3,故B选项错误;
C、x=﹣4时,y=﹣11,故C选项错误;
D、x=﹣3时,y=﹣9,故D选项正确.
故选:D.
点评:-本题考查了代数式求值,主要利用了二元一次方程的解,理解运算程序列出方程是解题的关键.
2.已知x2﹣2x﹣3=0,则2x2﹣4x的值为( )
A. ﹣6 B.6 C ﹣2或6 D. ﹣2或30
考点:-代数式求值.
专题:-整体思想.
分析:-方程两边同时乘以2,再化出2x2﹣4x求值.
解答:-解:x2﹣2x﹣3=0
2×(x2﹣2x﹣3)=0
2×(x2﹣2x)﹣6=0
2x2﹣4x=6
故选:B.
点评:-本题考查代数式求值,解题的关键是化出要求的2x2﹣4x.
3.当x=1时,代数式ax3﹣3bx+4的值是7,则当x=﹣1时,这个代数式的值是( )
A. 7 B.3 C 1 D. ﹣7
考点:-代数式求值.
专题:-整体思想.
分析:-把x=1代入代数式求出a、b的关系式,再把x=﹣1代入进行计算即可得解.
解答:-解:x=1时,ax3﹣3bx+4=a﹣3b+4=7,
解得a﹣3b=3,
当x=﹣1时,ax3﹣3bx+4=﹣a+3b+4=﹣3+4=1.
故选:C.
点评:-本题考查了代数式求值,整体思想的利用是解题的关键.
4.若m+n=﹣1,则(m+n)2﹣2m﹣2n的值是( )
A. 3 B.0 C 1 D. 2
考点:-代数式求值.
专题:-整体思想.
分析:-把(m+n)看作一个整体并代入所求代数式进行计算即可得解.
解答:-解:∵m+n=﹣1,
∴(m+n)2﹣2m﹣2n
=(m+n)2﹣2(m+n)
=(﹣1)2﹣2×(﹣1)
=1+2
=3.
故选:A.
点评:-本题考查了代数式求值,整体思想的利用是解题的关键.
5.若2a﹣b=3,则9﹣4a+2b的值为( )
A. 12 B.6 C.3 D. 0
考点:-代数式求值.
专题:-计算题.
分析:-所求式子后两项提取﹣2变形后,将2a﹣b的值代入计算即可求出值.
解答:-解:∵2a﹣b=3,
∴9﹣4a+2b=9﹣2(2a﹣b)=9﹣6=3.
故选C
点评:-此题考查了代数式求值,利用了整体代入的思想,将所求式子进行适当的变形是解本题的关键.
6.a、b经过运算后得到的结果如下表所示:
a 0.5 0.25
b 2 4
运算结果 4 16
下列可以得到上述运算结果的算式是( )
A. ab﹣1 B.a﹣1b C ab D. (ab)2
考点:-代数式求值;负整数指数幂.
分析:-根据表格数据,从负整数指数次幂等于正整数指数次幂的倒数考虑求解.
解答:-解:∵=4,=16,
∴表示运算结果的算式是a﹣1b.
故选B.
点评:-本题考查了代数式求值,从负整数指数幂考虑求解是解题的关键.
7.已知x2﹣2x﹣8=0,则3x2﹣6x﹣18的值为( )
A. 54 B.6 C ﹣10 D. ﹣18
考点:-代数式求值.
专题:-计算题.
分析:-所求式子前两项提取3变形后,将已知等式变形后代入计算即可求出值.
解答:-解:∵x2﹣2x﹣8=0,即x2﹣2x=8,
∴3x2﹣6x﹣18=3(x2﹣2x)﹣18=24﹣18=6.
故选B.
点评:-此题考查了代数式求值,利用了整体代入的思想,是一道基本题型.
8.当x=2时,代数式的值是( )
A. ﹣1 B.0 C 1 D. 1
考点:-代数式求值.
分析:-把x=2代入代数式进行计算即可得解.
解答:-解:x=2时,(﹣1)(x2﹣2x+1)=(﹣1)(12﹣2+1)=0.
故选B.
点评:-本题考查了代数式求值,是基础题,准确计算是解题的关键.
二.填空题(共7小题)
9.若m+n=0,则2m+2n+1= 1 .
考点:-代数式求值.
分析:-把所求代数式转化成已知条件的形式,然后整体代入进行计算即可得解.
解答:-解:∵m+n=0,
∴2m+2n+1=2(m+n)+1,
=2×0+1,
=0+1,
=1.
故答案为:1.
点评:-本题考查了代数式求值,整体思想的利用是解题的关键.
10.已知x(x+3)=1,则代数式2x2+6x﹣5的值为 ﹣3 .
考点:-代数式求值;单项式乘多项式.
专题:-整体思想.
分析:-把所求代数式整理出已知条件的形式,然后代入数据进行计算即可得解.
解答:-解:∵x(x+3)=1,
∴2x2+6x﹣5=2x(x+3)﹣5=2×1﹣5=2﹣5=﹣3.
s故答案为:﹣3.
点评:-本题考查了代数式求值,整体思想的利用是解题的关键.
11.若m2﹣2m﹣1=0,则代数式2m2﹣4m+3的值为 5 .
考点:-代数式求值.
专题:-整体思想.
分析:-先求出m2﹣2m的值,然后把所求代数式整理出已知条件的形式并代入进行计算即可得解.
解答:-解:由m2﹣2m﹣1=0得m2﹣2m=1,
所以,2m2﹣4m+3=2(m2﹣2m)+3=2×1+3=5.
故答案为:5.
点评:-本题考查了代数式求值,整体思想的利用是解题的关键.
12.如图是一个数值转换机的示意图,若输入x的值为3,y的值为﹣2时,则输出的结果为 5 .
( http: / / www.21cnjy.com )
考点:-代数式求值.
专题:-图表型.
分析:-把x=3,y=﹣2输入此程序即可.
解答:-解:把x=3,y=﹣2输入此程序得,
[3×2+(﹣2)2]÷2=10÷2=5.
点评:-解答本题的关键就是弄清楚题目给出的计算程序.
13.如果代数式5a+3b的值为﹣4,那么代数式2(a+b)+4(2a+b)的值为 ﹣8 .
考点:-代数式求值.
分析:-由于5a+3b的值为﹣4,故只需把要求的式子整理成含(5a+3b)的形式,代入求值即可.
解答:-解:∵5a+3b=﹣4,
∴原式=2a+2b+8a+4b=10a+6b=2(5a+3b)=2×(﹣4)=﹣8.
点评:-做此类题的时候,应先得到只含未知字母的代数式的值为多少,把要求的式子整理成包含那个代数式的形式.
b14.用“※”定义新运算:对于任意实数a,b,都有a※b=b2+1.例如,7※4=42+1=17,那么5※3= 10 .
考点:-代数式求值.
专题:-新定义.
分析:-熟悉新运算的计算规则,运用新规则计算.
解答:-解:依规则可知:5※3=32+1=10;
故答案为:10.
点评:-此题考查的知识点是代数式求值,关键是掌握新运算规则,然后再运用.
15.若实数a满足a2﹣2a﹣1=0,则2a2﹣4a+5= 7 .
考点:-代数式求值.
专题:-计算题.
分析:-根据a2﹣2a﹣1=0得出a2﹣2a=1,然后等式的左右两边同乘以2即可得到2a2﹣4a=2,再求2a2﹣4a+5的值就容易了.
解答:-解:∵a2﹣2a﹣1=0,
∴a2﹣2a=1,
∴2a2﹣4a=2,
∴2a2﹣4a+5=2+5=7.
故答案为7.
点评:-本题考查了代数式求值,解题的关键是求出2a2﹣4a的值,再代入2a2﹣4a+5即可.
三.解答题(共6小题)
16.已知当x=1时,2ax2+bx的值为﹣2,求当x=2时,ax2+bx的值.
考点:-代数式求值.
专题:-整体思想.
分析:-把x=1代入代数式求出a、b的关系式,再把x=2代入代数式整理即可得解.
解答:-解:将x=1代入2ax2+bx=﹣2中,
得2a+b=﹣2,
当x=2时,ax2+bx=4a+2b,
=2(2a+b),
=2×(﹣2),
=﹣4.
点评:-本题考查了代数式求值,整体思想的利用是解题的关键.
17.已知:x2﹣5x=6,请你求出代数式10x﹣2x2+5的值.
考点:-代数式求值.
专题:-整体思想.
分析:-先把10x﹣2x2+5变形为﹣2(x2﹣5x)+5,然后把x2﹣5x=6整体代入进行计算即可.
解答:-解:10x﹣2x2+5
=﹣2(x2﹣5x)+5,
∵x2﹣5x=6,
∴原式=﹣2×6+5=﹣12+5=﹣7.
点评:-本题考查了代数式求值:先根据已知条件把代数式进行变形,然后利用整体代入进行求值.
18.已知代数式3x2﹣4x+6值为9,则x2﹣+6的值.
考点:-代数式求值.
专题:-整体思想.
分析:-先根据题意列出等式3x2﹣4x+6=9,求得3x2﹣4x的值,然后求得x2﹣+6的值.
解答:-解:∵代数式3x2﹣4x+6值为9,∴3x2﹣4x+6=9,∴3x2﹣4x=3,
∴x2﹣=1,∴x2﹣+6=1+6=7.
点评:-本题考查了求代数式的值,找出未知与已知的关系,然后运用整体代入的思想.
19.2008年6月1日北京奥运圣火在宜昌 ( http: / / www.21cnjy.com )传递,圣火传递路线分为两段,其中在市区的传递路程为700(a﹣1)米,三峡坝区的传递路程为(881a+2309)米.设圣火在宜昌的传递总路程为s米,
(1)用含a的代数式表示s;
(2)已知a=11,求s的值.
考点:-代数式求值;列代数式.
专题:-计算题.
分析:-(1)中直接利用:总路程=市区的传递路程+三峡坝区的传递路程,代入相应的代数式,去括号,合并同类项,即可.
(2)已知a的值,求s,直接把a的值代入(1)中所得出的式子,即可求出s的值.
解答:-解:(1)s=700(a﹣1)+(881a+2309),
=1581a+1609;
(2)a=11时,
s=1581a+1609=1581×11+1609,
=19000.
点评:-此题的关键是找到题 ( http: / / www.21cnjy.com )目中给出的三个量的关系:总路程=市区的传递路程+三峡坝区的传递路程.然后把对应的数值或式子代入,根据要求解题即可.代数式求值问题是把字母的值直接代入相应的代数式即可.
20.如图所示是一个数表,现用一个矩形在数表中任意框出4个数,则
(1)a、c的关系是: a=c﹣5 ;
(2)当a+b+c+d=32时,a= 5 .
( http: / / www.21cnjy.com )
考点:-代数式求值;列代数式;一元一次方程的应用.
专题:-压轴题;图表型.
分析:-(1)结合图任意列举两组数字,即可发现a与c的关系;
(2)根据已知条件列一元一次方程求解即可.
解答:-解:(1)当a为4时,c=9,∴c﹣a=5,即a=c﹣5,
当a=9时,c=14,
∴c﹣a=5,即a=c﹣5,
∴a、c的关系是:a=c﹣5;
(2)设a=x,则b=x+1,c=x+5,d=x+6,
∵a+b+c+d=32,
∴x+x+1+x+5+x+6=32,
解得x=5,
∴a=5.
点评:-本题考查了代数式求值和一元一次方程的应用,解题的关键是结合图表弄清题意.
21.已知a、b互为相反数,c、d互为倒数,|d|=2,x2=4,求:
(1)2x12的值;
(2)(a+b)+﹣的值.
考点:-代数式求值;相反数;绝对值;倒数;有理数的乘方.
专题:-计算题.
分析:-(1)原式利用幂的乘方运算法则变形,将x2=4代入计算即可求出值;
(2)利用相反数,倒数的定义,平方根定义,以及绝对值的代数意义,求出a+b,cd,x的值,代入原式计算即可得到结果.
解答:-解:(1)∵x2=4,
∴2x12=2(x2)6=2×46=8192;
(2)根据题意得:a+b=0,cd=1,d=2或﹣2,x=2或﹣2,
则原式=0+2﹣0=2.
点评:-此题考查了代数式求值,以及非负数的性质,熟练掌握运算法则是解本题的关键.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
