【核心素养目标】苏科版八年级数学上册5.2 第1课时 平面直角坐标系 课件 (共30张PPT)
文档属性
| 名称 | 【核心素养目标】苏科版八年级数学上册5.2 第1课时 平面直角坐标系 课件 (共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 888.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-28 00:00:00 | ||
图片预览











文档简介
(共30张PPT)
第5章 平面直角坐标系
5.2 平面直角坐标系
第1课时 平面直角坐标系
1.领会实际模型中确定位置的方法,会正确画出平面直角坐标系.
2.在给定的平面直角坐标系中,会根据点的坐标描出点的位置,由点的位置写出点的坐标.
3.知道各象限内点的坐标的符号特点,坐标轴上点的坐标特点.
◎重点:在给定的平面直角坐标系中,根据点的坐标描出点的位置,由点的位置写出点的坐标.
◎难点:各象限内点的坐标的符号特点,坐标轴上点的坐标特点.
1.分别在括号中写出数轴上点表示的数:
A.( ) B.( ) C.( ) D.( ) E.( )
2.在数轴上分别画出如下的点的位置:
A(-1) B(2) C(0.5) D(0) E(-6)
平面直角坐标系与点的坐标
阅读课本本课时开始到例2前的内容,回答下列问题:
1.平面直角坐标系
平面内两条互相 垂直 的数轴构成平面直角坐标系,简称 直角坐标系 .水平的数轴称为 x 轴或 横 轴,规定向 右 的方向为正方向;竖直的数轴称为 y 轴或 纵 轴,规定向 上 的方向为正方向;两坐标轴的交点O为平面直角坐标系的 原点 .
垂直
直角坐标系
x
横
右
y
纵
上
原点
2.点的坐标
(1)在平面直角坐标系中,一对有序实数可以确定一个点的位置;反之,任意一点的位置都可以用一对有序实数来表示.这样的有序实数对叫做点的 坐标 .过点P作x轴的垂线,垂足对应的是a;过点P作y轴的垂线,垂足对应的是b;则点P的坐标为 (a,b) ,a叫做点P的 横 坐标,b叫做点P的 纵 坐标.
坐标
(a,b)
横
纵
(2)点的坐标通常与表示该点的大写字母写在一起,如P(a,b),Q(m,n).
温馨提示 1.在判断平面直角坐标系时,一定要注意以下几点:垂直,公共原点,正方向,单位长度,可类比数轴.
2.垂足在横轴上对应的数叫做点的横坐标,垂足在纵轴上对应的数叫做点的纵坐标.横坐标写在前,纵坐标写在后,中间用逗号隔开.
如图,在平面直角坐标系中.
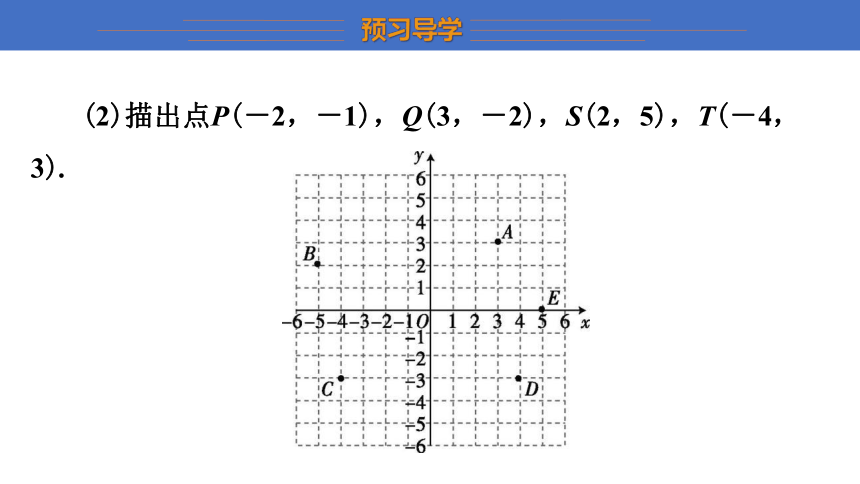
(1)写出点A,B,C,D,E的坐标.
解:(1)A(3,3),B(-5,2),C(-4,-3),D(4,-3),E(5,0).
(2)描出点P(-2,-1),Q(3,-2),S(2,5),T(-4,3).
解:(2)点P(-2,-1),Q(3,-2),S(2,5),T(-4,3)的位置如图所示.
解:(2)点P(-2,-1),Q(3,-2),S(2,5),T(-4,3)
的位置如图所示.
平面直角坐标系内点的坐标特点
阅读课本本课时例2及讨论的内容,回答下列问题:
1.两条坐标轴将平面分成的4个区域称为象限,如图:
2.任意找出几个位于第一象限的点,观察它们的坐标特点,我们发现这些点的横坐标都是 正 的,纵坐标都是 正 的.(填“正”或“负”)
3.任意找出几个位于第二象限的点,可以发现它们的横坐标都是 负 的,纵坐标都是 正 的.(填“正”或“负”)
4.任意找出几个位于第三象限的点,可以发现它们的横坐标都是 负 的,纵坐标都是 负 的.(填“正”或“负”)
正
正
负
正
负
负
5.任意找出几个位于第四象限的点,可以发现它们的横坐标都是 正 的,纵坐标都是 负 的.(填“正”或“负”)
归纳总结 1.直角坐标系内,各象限的点的坐标的符号特征:第一象限为 (+,+) ,第二象限为
(-,+) ,第三象限为 (-,-) ,第四象限为 (+,-) .
正
负
(+,+)
(-,+)
(-,-)
(+,-)
2.坐标轴不属于任何象限
讨论 若某个点的坐标特征为(+,+),你能判断它所在的象限吗?若为(-,+)呢?若为(-,-)呢?若为(+,-)呢?
它们分别位于第一象限,第二象限,第三象限,第四象限.
·导学建议·
1.通过平面直角坐标系,学生可总结出各象限的点的符号特征,为了验证其正确性,可再举几例.2.注意渗透分类讨论思想:对于“点在坐标轴上”这句话,应该从两方面分析:(1)点在x轴上;(2)点在y轴上.
归纳总结 1.x轴上的点的 纵 坐标为0;y轴上的点的 坐标为0.
纵
横
2.平行于x轴的直线上各点的 纵 坐标相同;平行于y轴的直线上各点的 横 坐标相同.
纵
横
1.点E(-2,0)在 x 轴上,点F(0,3)在 y 轴上.
2.点A(3,-4)在第 四 象限,点B(-2,-3)在第 三 象限,点C(-3,4)在第 二 象限,点D(2,3)在第 一 象限.
x
y
四
三
二
一
1.点A(3,-4)在第 四 象限,横坐标是 3 ,纵坐标是 -4 ;到x轴的距离是 4 ,到y轴的距离是 3 ,到原点的距离是 5 .
四
3
-4
4
3
5
方法归纳交流 点P(a,b)到x轴的距离是 |b| ,到y轴的距离是 |a| ,到原点的距离是 (用a,b表示).
|b|
|a|
2.已知点A(m+1,-2),B(3,m-1).
(1)若直线AB∥x轴,则m的值为 ;
(2)若直线AB∥y轴,则m的值为 .
解析:(1)因为直线AB∥x轴,所以A,B两点的纵坐标相等,即m-1=-2,解得m=-1.
(2)因为直线AB∥y轴,所以A,B两点的横坐标相等,即m+1=3,解得m=2.
方法归纳交流
1.如果直线l1∥x轴,那么直线l1上的所有点到x轴的距离相等,即纵坐标相等.
2.如果直线l2∥y轴,那么直线l2上的所有点到y轴的距离都相等,即横坐标相等.
变式演练 已知线段AB∥y轴,若点A的坐标为(5,n-1),B(n2+1,1),则n为 -2 .
-2
3.若点(6-2x,x+6)到两坐标轴的距离相等,则该点的坐标为 (6,6)或(-18,18) .
归纳总结
坐标有正负之分,距离则是一个长度.本题易只考虑其中一种情况,而丢掉(-18,18)的解.
(6,6)或(-18,18)
变式演练 已知点P的坐标为(2-a,6),且点P到两坐标轴的距离相等,则a的值为 -4或8 .
-4或8
4.如图,这是一个在平面直角坐标系中从原点开始的回形图,其中回形通道的宽和OA的长都是1.
(1)根据图形填表格:
点 坐标 所在象限或坐标轴
A (0,1) y轴
B (1,1) 第一象限
C (1,-1) 第四象限
(0,1)
y轴
(1,1)
第一象限
(1,-1)
第四象限
点 坐标 所在象限或坐标轴
D (-1,-1) 第三象限
E (-1,2) 第二象限
F (2,2) 第一象限
(2)在图上将回形图继续画下一步到G点,写出G点坐标: (2,-2) .
(-1,-1)
第三象限
(-1,2)
第二象限
(2,2)
第一象限
(2,-2)
1.如图,在阴影区域的点是( B )
A.(1,2) B.(-1,2)
C.(-1,-2) D.(1,-2)
B
2.点P在第二象限,若该点到x轴的距离为3,到y轴的距离为1,则点P的坐标是( A )
A.(-1,3) B.(-3,1)
C.(3,-1) D.(1,3)
3.在平面直角坐标系中,若点P(m-3,m+1)到两坐标轴的距离相等,则m的值为 1 .
A
1
第5章 平面直角坐标系
5.2 平面直角坐标系
第1课时 平面直角坐标系
1.领会实际模型中确定位置的方法,会正确画出平面直角坐标系.
2.在给定的平面直角坐标系中,会根据点的坐标描出点的位置,由点的位置写出点的坐标.
3.知道各象限内点的坐标的符号特点,坐标轴上点的坐标特点.
◎重点:在给定的平面直角坐标系中,根据点的坐标描出点的位置,由点的位置写出点的坐标.
◎难点:各象限内点的坐标的符号特点,坐标轴上点的坐标特点.
1.分别在括号中写出数轴上点表示的数:
A.( ) B.( ) C.( ) D.( ) E.( )
2.在数轴上分别画出如下的点的位置:
A(-1) B(2) C(0.5) D(0) E(-6)
平面直角坐标系与点的坐标
阅读课本本课时开始到例2前的内容,回答下列问题:
1.平面直角坐标系
平面内两条互相 垂直 的数轴构成平面直角坐标系,简称 直角坐标系 .水平的数轴称为 x 轴或 横 轴,规定向 右 的方向为正方向;竖直的数轴称为 y 轴或 纵 轴,规定向 上 的方向为正方向;两坐标轴的交点O为平面直角坐标系的 原点 .
垂直
直角坐标系
x
横
右
y
纵
上
原点
2.点的坐标
(1)在平面直角坐标系中,一对有序实数可以确定一个点的位置;反之,任意一点的位置都可以用一对有序实数来表示.这样的有序实数对叫做点的 坐标 .过点P作x轴的垂线,垂足对应的是a;过点P作y轴的垂线,垂足对应的是b;则点P的坐标为 (a,b) ,a叫做点P的 横 坐标,b叫做点P的 纵 坐标.
坐标
(a,b)
横
纵
(2)点的坐标通常与表示该点的大写字母写在一起,如P(a,b),Q(m,n).
温馨提示 1.在判断平面直角坐标系时,一定要注意以下几点:垂直,公共原点,正方向,单位长度,可类比数轴.
2.垂足在横轴上对应的数叫做点的横坐标,垂足在纵轴上对应的数叫做点的纵坐标.横坐标写在前,纵坐标写在后,中间用逗号隔开.
如图,在平面直角坐标系中.
(1)写出点A,B,C,D,E的坐标.
解:(1)A(3,3),B(-5,2),C(-4,-3),D(4,-3),E(5,0).
(2)描出点P(-2,-1),Q(3,-2),S(2,5),T(-4,3).
解:(2)点P(-2,-1),Q(3,-2),S(2,5),T(-4,3)的位置如图所示.
解:(2)点P(-2,-1),Q(3,-2),S(2,5),T(-4,3)
的位置如图所示.
平面直角坐标系内点的坐标特点
阅读课本本课时例2及讨论的内容,回答下列问题:
1.两条坐标轴将平面分成的4个区域称为象限,如图:
2.任意找出几个位于第一象限的点,观察它们的坐标特点,我们发现这些点的横坐标都是 正 的,纵坐标都是 正 的.(填“正”或“负”)
3.任意找出几个位于第二象限的点,可以发现它们的横坐标都是 负 的,纵坐标都是 正 的.(填“正”或“负”)
4.任意找出几个位于第三象限的点,可以发现它们的横坐标都是 负 的,纵坐标都是 负 的.(填“正”或“负”)
正
正
负
正
负
负
5.任意找出几个位于第四象限的点,可以发现它们的横坐标都是 正 的,纵坐标都是 负 的.(填“正”或“负”)
归纳总结 1.直角坐标系内,各象限的点的坐标的符号特征:第一象限为 (+,+) ,第二象限为
(-,+) ,第三象限为 (-,-) ,第四象限为 (+,-) .
正
负
(+,+)
(-,+)
(-,-)
(+,-)
2.坐标轴不属于任何象限
讨论 若某个点的坐标特征为(+,+),你能判断它所在的象限吗?若为(-,+)呢?若为(-,-)呢?若为(+,-)呢?
它们分别位于第一象限,第二象限,第三象限,第四象限.
·导学建议·
1.通过平面直角坐标系,学生可总结出各象限的点的符号特征,为了验证其正确性,可再举几例.2.注意渗透分类讨论思想:对于“点在坐标轴上”这句话,应该从两方面分析:(1)点在x轴上;(2)点在y轴上.
归纳总结 1.x轴上的点的 纵 坐标为0;y轴上的点的 坐标为0.
纵
横
2.平行于x轴的直线上各点的 纵 坐标相同;平行于y轴的直线上各点的 横 坐标相同.
纵
横
1.点E(-2,0)在 x 轴上,点F(0,3)在 y 轴上.
2.点A(3,-4)在第 四 象限,点B(-2,-3)在第 三 象限,点C(-3,4)在第 二 象限,点D(2,3)在第 一 象限.
x
y
四
三
二
一
1.点A(3,-4)在第 四 象限,横坐标是 3 ,纵坐标是 -4 ;到x轴的距离是 4 ,到y轴的距离是 3 ,到原点的距离是 5 .
四
3
-4
4
3
5
方法归纳交流 点P(a,b)到x轴的距离是 |b| ,到y轴的距离是 |a| ,到原点的距离是 (用a,b表示).
|b|
|a|
2.已知点A(m+1,-2),B(3,m-1).
(1)若直线AB∥x轴,则m的值为 ;
(2)若直线AB∥y轴,则m的值为 .
解析:(1)因为直线AB∥x轴,所以A,B两点的纵坐标相等,即m-1=-2,解得m=-1.
(2)因为直线AB∥y轴,所以A,B两点的横坐标相等,即m+1=3,解得m=2.
方法归纳交流
1.如果直线l1∥x轴,那么直线l1上的所有点到x轴的距离相等,即纵坐标相等.
2.如果直线l2∥y轴,那么直线l2上的所有点到y轴的距离都相等,即横坐标相等.
变式演练 已知线段AB∥y轴,若点A的坐标为(5,n-1),B(n2+1,1),则n为 -2 .
-2
3.若点(6-2x,x+6)到两坐标轴的距离相等,则该点的坐标为 (6,6)或(-18,18) .
归纳总结
坐标有正负之分,距离则是一个长度.本题易只考虑其中一种情况,而丢掉(-18,18)的解.
(6,6)或(-18,18)
变式演练 已知点P的坐标为(2-a,6),且点P到两坐标轴的距离相等,则a的值为 -4或8 .
-4或8
4.如图,这是一个在平面直角坐标系中从原点开始的回形图,其中回形通道的宽和OA的长都是1.
(1)根据图形填表格:
点 坐标 所在象限或坐标轴
A (0,1) y轴
B (1,1) 第一象限
C (1,-1) 第四象限
(0,1)
y轴
(1,1)
第一象限
(1,-1)
第四象限
点 坐标 所在象限或坐标轴
D (-1,-1) 第三象限
E (-1,2) 第二象限
F (2,2) 第一象限
(2)在图上将回形图继续画下一步到G点,写出G点坐标: (2,-2) .
(-1,-1)
第三象限
(-1,2)
第二象限
(2,2)
第一象限
(2,-2)
1.如图,在阴影区域的点是( B )
A.(1,2) B.(-1,2)
C.(-1,-2) D.(1,-2)
B
2.点P在第二象限,若该点到x轴的距离为3,到y轴的距离为1,则点P的坐标是( A )
A.(-1,3) B.(-3,1)
C.(3,-1) D.(1,3)
3.在平面直角坐标系中,若点P(m-3,m+1)到两坐标轴的距离相等,则m的值为 1 .
A
1
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
