【核心素养目标】北师大版数学八年级下册6.3 三角形中位线 课件(共17张PPT)
文档属性
| 名称 | 【核心素养目标】北师大版数学八年级下册6.3 三角形中位线 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 436.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-28 20:20:45 | ||
图片预览



文档简介
(共17张PPT)
我们学校有一块三角形空地,如图所示,为了美化校园,计划栽种两种花草,需将该空地分成面积相等的两部分,请大家帮忙设计合理的解决方案。
创设情境,导入新课
三角形的中位线
两层含义
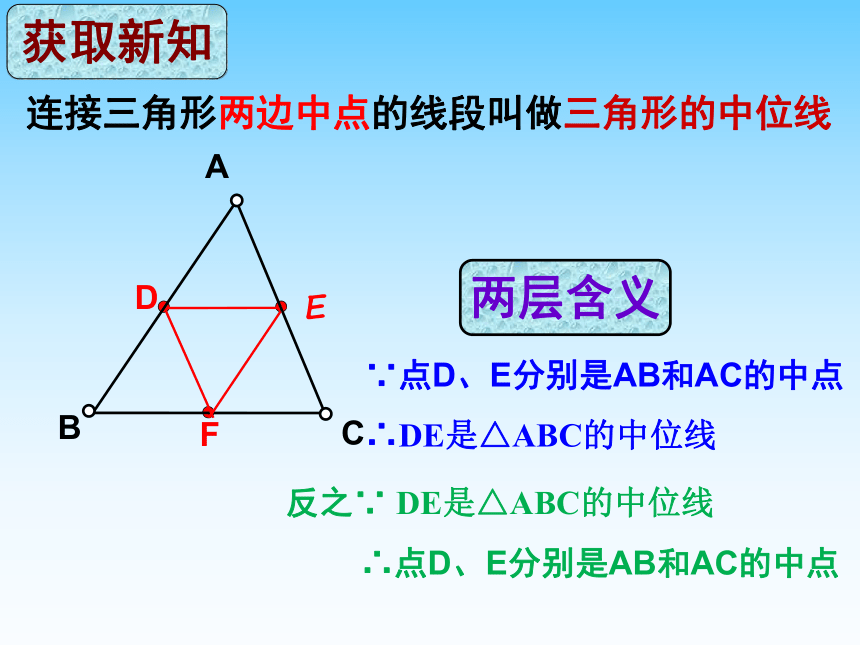
连接三角形两边中点的线段叫做三角形的中位线
∵点D、E分别是AB和AC的中点
∴DE是△ABC的中位线
反之∵ DE是△ABC的中位线
∴点D、E分别是AB和AC的中点
E
D
F
A
C
B
获取新知
说一说
A
B
C
D
E
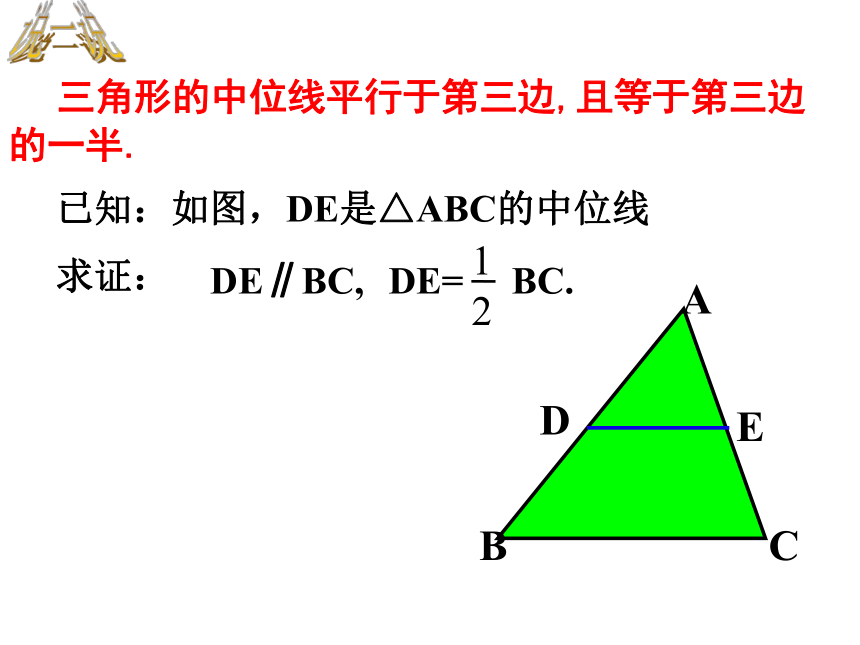
三角形的中位线平行于第三边,且等于第三边的一半.
已知:如图,DE是△ABC的中位线
求证:
DE∥BC,
DE= BC.
2
1
E
A
B
C
D
F
证明:如 图,延 长DE 到 F,使FE=DE 连 接CF.
∵DE=FE ,∠AED=∠CEF ,
AE=CE
∴△ADE ≌ △CFE(SAS)
∴AD=CF ,∠A=∠ECF
∴AB∥CF
∵ AD=DB
∴BD∥ FC且 BD =FC
∴四边形BCFD是平行四边形
∴DF∥CB,DF=CB
即DE∥BC
又∵
A
B
C
D
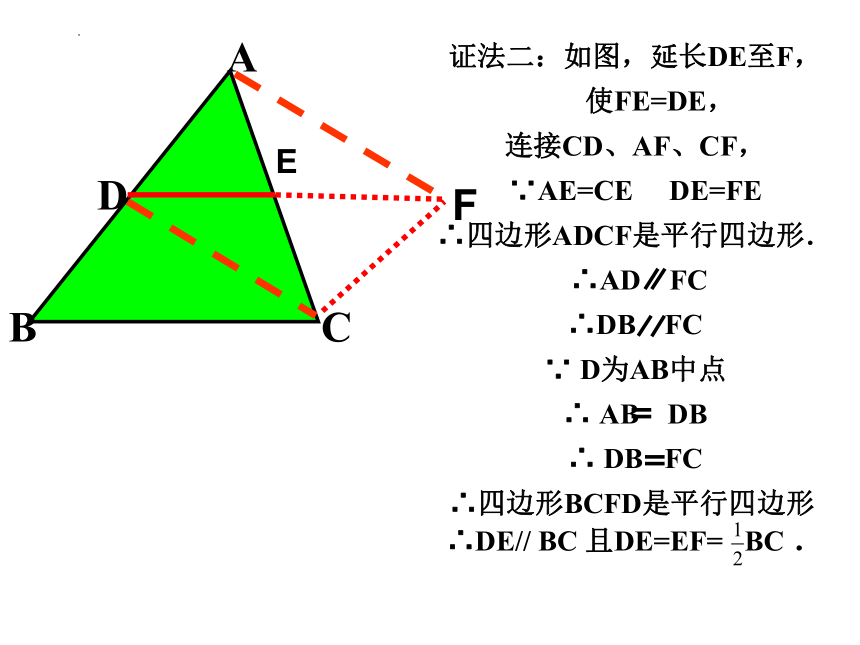
证法二:如图,延长DE至F,
使FE=DE,
连接CD、AF、CF,
∵AE=CE DE=FE
∴四边形ADCF是平行四边形.
∴AD FC
∴DB FC
∵ D为AB中点
∴ AB DB
∴ DB FC
∴四边形BCFD是平行四边形
∴DE// BC 且DE=EF= BC .
F
E
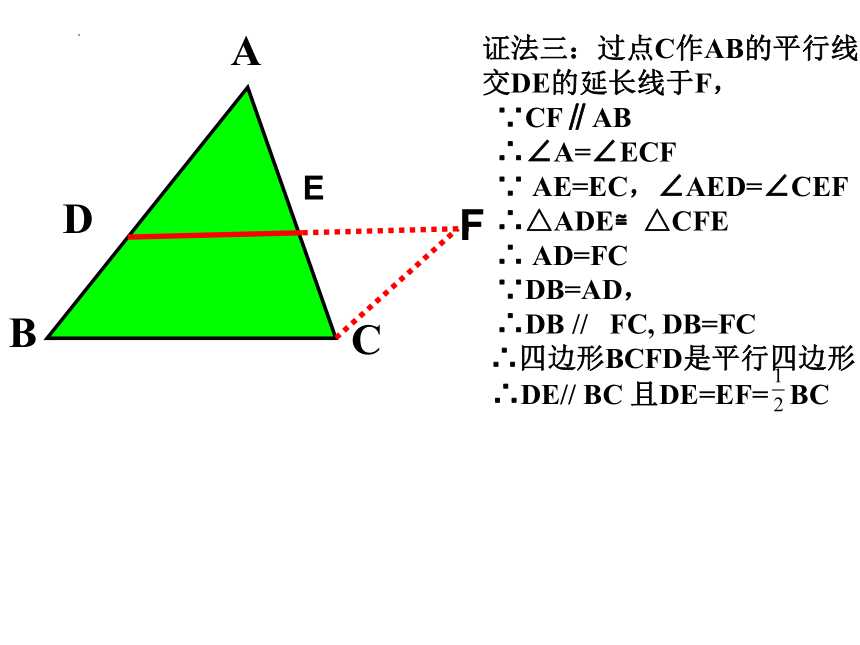
证法三:过点C作AB的平行线
交DE的延长线于F,
∵CF∥AB
∴∠A=∠ECF
∵ AE=EC,∠AED=∠CEF
∴△ADE≌△CFE
∴ AD=FC
∵DB=AD,
∴DB // FC, DB=FC
∴四边形BCFD是平行四边形
∴DE// BC 且DE=EF= BC
A
B
C
D
F
E
三角形中位线定理
三角形的中位线平行第三边,且等于第三边的一半.
∵DE是△ABC的中位线
C
E
D
B
A
∴DE ∥BC
DE= BC.
A
C
B
E
D
F
初试身手
练习1.如图,在△ABC中,D、E分别是AB、AC的中点
若∠ADE=65°,则∠B= 度,为什么?
若BC=8cm,则DE= cm,为什么?
65
4
若AC=4cm,BC=6cm,AB=8cm,
则△DEF的周长=______
练习1.如图,在△ABC中,D、E、F分别是AB、AC、BC的中点
9cm
若△ABC的周长为24,△DEF的周长是_____
12
图中有_____个平行四边形
3
定理应用
已知:如图,A,B两地被池塘隔开,在没有任何测量工具的情况下,小明通过学习,估测出了A,B两地之间的距离:先在AB外选一点C,然后步测出AC,BC的中点M,N,并测出MN的长,由此他就知道了A,B间的距离.你能说出其中的道理吗
C
M
B
A
N
我们学校有一块三角形空地,如图所示,为了美化校园,计划栽种四种花草,需将该空地分成面积相等的四部分,请大家帮忙设计合理的解决方案。
如果需将该空地分成面积,形状都相同的四部分呢?
设 计 方 案:
F
D
E
A
B
C
已知:如图,在四边形ABCD中,E、F、G、H分别是 AB、BC、CD、DA的中点.
猜想四边形EFGH的形状并证明。
A
B
C
D
E
F
G
H
理由如下:如图,连接AC
∵EF是△ABC的中位线
同理得:
∴四边形EFGH是平行四边形
延伸拓广
解: 四边形EFGH为平行四边形。
中考链接
(2013.烟台中考)如图所示,平行四边形ABCD的周长为36,对角线AC,BD相交于点O.点E是CD的中点,BD=12,则△DOE的周长为_____
15
说一说你学到了什么
?
美国著名数学家哈尔莫斯曾经说过“学习数学的真正部分是问题的解”
毋庸置疑,学习数学就意味着解题。解题,联想是基础,转化是手段,灵活运用是关键,问题解决是目的。
小结
1、三角形中位线的定义
2、三角形中位线定理
连接三角形两边中点的线段叫做三角形的中位线
三角形的中位线平行于三角形的第三边,且等于第三边的一半
我们学校有一块三角形空地,如图所示,为了美化校园,计划栽种两种花草,需将该空地分成面积相等的两部分,请大家帮忙设计合理的解决方案。
创设情境,导入新课
三角形的中位线
两层含义
连接三角形两边中点的线段叫做三角形的中位线
∵点D、E分别是AB和AC的中点
∴DE是△ABC的中位线
反之∵ DE是△ABC的中位线
∴点D、E分别是AB和AC的中点
E
D
F
A
C
B
获取新知
说一说
A
B
C
D
E
三角形的中位线平行于第三边,且等于第三边的一半.
已知:如图,DE是△ABC的中位线
求证:
DE∥BC,
DE= BC.
2
1
E
A
B
C
D
F
证明:如 图,延 长DE 到 F,使FE=DE 连 接CF.
∵DE=FE ,∠AED=∠CEF ,
AE=CE
∴△ADE ≌ △CFE(SAS)
∴AD=CF ,∠A=∠ECF
∴AB∥CF
∵ AD=DB
∴BD∥ FC且 BD =FC
∴四边形BCFD是平行四边形
∴DF∥CB,DF=CB
即DE∥BC
又∵
A
B
C
D
证法二:如图,延长DE至F,
使FE=DE,
连接CD、AF、CF,
∵AE=CE DE=FE
∴四边形ADCF是平行四边形.
∴AD FC
∴DB FC
∵ D为AB中点
∴ AB DB
∴ DB FC
∴四边形BCFD是平行四边形
∴DE// BC 且DE=EF= BC .
F
E
证法三:过点C作AB的平行线
交DE的延长线于F,
∵CF∥AB
∴∠A=∠ECF
∵ AE=EC,∠AED=∠CEF
∴△ADE≌△CFE
∴ AD=FC
∵DB=AD,
∴DB // FC, DB=FC
∴四边形BCFD是平行四边形
∴DE// BC 且DE=EF= BC
A
B
C
D
F
E
三角形中位线定理
三角形的中位线平行第三边,且等于第三边的一半.
∵DE是△ABC的中位线
C
E
D
B
A
∴DE ∥BC
DE= BC.
A
C
B
E
D
F
初试身手
练习1.如图,在△ABC中,D、E分别是AB、AC的中点
若∠ADE=65°,则∠B= 度,为什么?
若BC=8cm,则DE= cm,为什么?
65
4
若AC=4cm,BC=6cm,AB=8cm,
则△DEF的周长=______
练习1.如图,在△ABC中,D、E、F分别是AB、AC、BC的中点
9cm
若△ABC的周长为24,△DEF的周长是_____
12
图中有_____个平行四边形
3
定理应用
已知:如图,A,B两地被池塘隔开,在没有任何测量工具的情况下,小明通过学习,估测出了A,B两地之间的距离:先在AB外选一点C,然后步测出AC,BC的中点M,N,并测出MN的长,由此他就知道了A,B间的距离.你能说出其中的道理吗
C
M
B
A
N
我们学校有一块三角形空地,如图所示,为了美化校园,计划栽种四种花草,需将该空地分成面积相等的四部分,请大家帮忙设计合理的解决方案。
如果需将该空地分成面积,形状都相同的四部分呢?
设 计 方 案:
F
D
E
A
B
C
已知:如图,在四边形ABCD中,E、F、G、H分别是 AB、BC、CD、DA的中点.
猜想四边形EFGH的形状并证明。
A
B
C
D
E
F
G
H
理由如下:如图,连接AC
∵EF是△ABC的中位线
同理得:
∴四边形EFGH是平行四边形
延伸拓广
解: 四边形EFGH为平行四边形。
中考链接
(2013.烟台中考)如图所示,平行四边形ABCD的周长为36,对角线AC,BD相交于点O.点E是CD的中点,BD=12,则△DOE的周长为_____
15
说一说你学到了什么
?
美国著名数学家哈尔莫斯曾经说过“学习数学的真正部分是问题的解”
毋庸置疑,学习数学就意味着解题。解题,联想是基础,转化是手段,灵活运用是关键,问题解决是目的。
小结
1、三角形中位线的定义
2、三角形中位线定理
连接三角形两边中点的线段叫做三角形的中位线
三角形的中位线平行于三角形的第三边,且等于第三边的一半
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
