【核心素养目标】苏科版七年级数学上册6.3 第1课时 余角、补角 课件 (共16张PPT)
文档属性
| 名称 | 【核心素养目标】苏科版七年级数学上册6.3 第1课时 余角、补角 课件 (共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 725.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-28 20:23:23 | ||
图片预览






文档简介
(共16张PPT)
第6章 平面图形的认识(一)
6.3 余角、补角、对顶角
第1课时 余角、补角
1.知道互为余角、互为补角的概念,能求一个角的余角和补角;
2.明确余角、补角的性质定理,并能够运用其解决相关数学问题;
3.知道同角(等角)的余角相等,知道同角(等角)的补角相等.
◎重点:余角、补角的概念和性质.
◎难点:利用余角、补角的概念求角的度数.
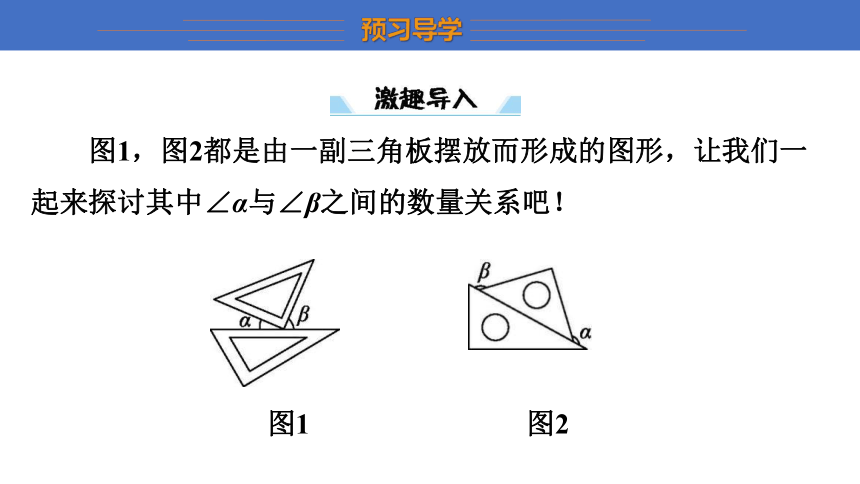
图1,图2都是由一副三角板摆放而形成的图形,让我们一起来探讨其中∠α与∠β之间的数量关系吧!
图1 图2
学生通过摆放三角板的位置,探究角度之间的关系.
·导学建议·
互余和互补的概念
阅读课本本课时第159页至第160页“议一议”之前的内容,回答下列问题.
1.如果两个角的和等于 90° ,就说这两个角互为余角,即其中任意一个角都是另一个角的 余角 .
2.如果两个角的和等于 180° ,就说这两个角互为补角,即其中任意一个角都是另一个角的 补角 .
90°
余角
180°
补角
3.思考:(1)互补、互余的两角是否一定有公共顶点或公共边呢?
不一定.
(2)∠1+∠2=90°,能否说∠1是余角,∠2是余角呢?为什么?∠1+∠2=180°呢?
不能,应说成∠1和∠2互余,∠1是∠2的余角或∠2是∠1的余角.互余、互补是针对两个角而言.∠1与∠2互补.
互余与互补的性质
阅读课本本课时第160页“议一议”及例1的内容,回答下列问题.
1.已知∠1与∠α互余,∠2与∠β互余,即∠1+∠α= 90° ,∠2+∠β= 90° ,如果∠α=∠β,即∠α与∠β是等角,那么∠1与∠2 相等 .
90°
90°
相等
2.已知∠1与∠α互补,∠2与∠β互补,即∠1+∠α= 180° ,∠2+∠β= 180° ,如果∠α=∠β,即∠α与∠β是等角,那么∠1与∠2 相等 .
归纳总结 同角(等角) 的余角相等, 同角(等角) 的补角相等.
180°
180°
相等
同角(等角)
同角(等角)
1.若∠A=34°,则∠A的余角为( A )
A.56° B.146°
C.46° D.66°
2.若∠1+∠2=90°,∠1+∠3=90°,则∠2与∠3的关系是( A )
A.∠2=∠3 B.∠2>∠3
C.∠2<∠3 D.不能确定
A
A
3.一个角比它的补角的少40°,这个角等于 15° .
15°
余角和补角的有关计算
1.25°的余角和补角分别是多少度?一个角的补角比它的余角大多少度?
解:65°,155°.设这个角的度数为x,则它的补角的度数为180-x,它的余角的度数为90-x,(180-x)-(90-x)=90,即这个角的补角比它的余角大90°.
变式训练 一个角的余角比它的补角的还多1°,求这个角的度数.
(方法指导:在解决几何问题时,常设未知数列方程求解,即将几何问题转化为代数问题)
解:设这个角的度数为x°,则90-x=(180-x)+1,解得x=63.
答:这个角的度数为63°.
余角和补角的性质
2.如图,点O是直线AB上一点,OC平分∠AOB,∠DOE=90°,∠AOD和∠COE相等吗?为什么?
解:∠AOD=∠COE.
理由:因为OC平分∠AOB,所以∠AOC=
∠BOC=90°,所以∠AOD+∠COD=90°.
又因为∠COE+∠COD=90°,所以∠AOD=∠COE.
变式训练 除直角外,上题中还有哪些相等的角?请说明理由.
解:∠COD=∠BOE.
理由:因为∠COE+∠COD=90°,∠COE+∠BOE=90°,
由同角的余角相等得∠COD=∠BOE.
方法归纳交流 要说明两个角相等,只要说明这两个角是 同一个角 的余角(或补角)即可.
·导学建议·
同一个角
互余和互补主要反映的是角的数量关系,而不是角的位置关系.通过合作探究的学习,更好地达成本课时学习目标.
1.下列说法正确的是( A )
A.锐角的补角一定是钝角
B.一个角的补角一定大于这个角
C.锐角和钝角一定互补
D.两个锐角一定互为余角
A
2.如图,∠AOD=∠DOB=∠COE=90°,互补的角有
( C )
A.5对 B.6对 C.7对 D.8对
3.若∠α的补角是它的3倍,则∠α的度数为 45° .
C
45°
第6章 平面图形的认识(一)
6.3 余角、补角、对顶角
第1课时 余角、补角
1.知道互为余角、互为补角的概念,能求一个角的余角和补角;
2.明确余角、补角的性质定理,并能够运用其解决相关数学问题;
3.知道同角(等角)的余角相等,知道同角(等角)的补角相等.
◎重点:余角、补角的概念和性质.
◎难点:利用余角、补角的概念求角的度数.
图1,图2都是由一副三角板摆放而形成的图形,让我们一起来探讨其中∠α与∠β之间的数量关系吧!
图1 图2
学生通过摆放三角板的位置,探究角度之间的关系.
·导学建议·
互余和互补的概念
阅读课本本课时第159页至第160页“议一议”之前的内容,回答下列问题.
1.如果两个角的和等于 90° ,就说这两个角互为余角,即其中任意一个角都是另一个角的 余角 .
2.如果两个角的和等于 180° ,就说这两个角互为补角,即其中任意一个角都是另一个角的 补角 .
90°
余角
180°
补角
3.思考:(1)互补、互余的两角是否一定有公共顶点或公共边呢?
不一定.
(2)∠1+∠2=90°,能否说∠1是余角,∠2是余角呢?为什么?∠1+∠2=180°呢?
不能,应说成∠1和∠2互余,∠1是∠2的余角或∠2是∠1的余角.互余、互补是针对两个角而言.∠1与∠2互补.
互余与互补的性质
阅读课本本课时第160页“议一议”及例1的内容,回答下列问题.
1.已知∠1与∠α互余,∠2与∠β互余,即∠1+∠α= 90° ,∠2+∠β= 90° ,如果∠α=∠β,即∠α与∠β是等角,那么∠1与∠2 相等 .
90°
90°
相等
2.已知∠1与∠α互补,∠2与∠β互补,即∠1+∠α= 180° ,∠2+∠β= 180° ,如果∠α=∠β,即∠α与∠β是等角,那么∠1与∠2 相等 .
归纳总结 同角(等角) 的余角相等, 同角(等角) 的补角相等.
180°
180°
相等
同角(等角)
同角(等角)
1.若∠A=34°,则∠A的余角为( A )
A.56° B.146°
C.46° D.66°
2.若∠1+∠2=90°,∠1+∠3=90°,则∠2与∠3的关系是( A )
A.∠2=∠3 B.∠2>∠3
C.∠2<∠3 D.不能确定
A
A
3.一个角比它的补角的少40°,这个角等于 15° .
15°
余角和补角的有关计算
1.25°的余角和补角分别是多少度?一个角的补角比它的余角大多少度?
解:65°,155°.设这个角的度数为x,则它的补角的度数为180-x,它的余角的度数为90-x,(180-x)-(90-x)=90,即这个角的补角比它的余角大90°.
变式训练 一个角的余角比它的补角的还多1°,求这个角的度数.
(方法指导:在解决几何问题时,常设未知数列方程求解,即将几何问题转化为代数问题)
解:设这个角的度数为x°,则90-x=(180-x)+1,解得x=63.
答:这个角的度数为63°.
余角和补角的性质
2.如图,点O是直线AB上一点,OC平分∠AOB,∠DOE=90°,∠AOD和∠COE相等吗?为什么?
解:∠AOD=∠COE.
理由:因为OC平分∠AOB,所以∠AOC=
∠BOC=90°,所以∠AOD+∠COD=90°.
又因为∠COE+∠COD=90°,所以∠AOD=∠COE.
变式训练 除直角外,上题中还有哪些相等的角?请说明理由.
解:∠COD=∠BOE.
理由:因为∠COE+∠COD=90°,∠COE+∠BOE=90°,
由同角的余角相等得∠COD=∠BOE.
方法归纳交流 要说明两个角相等,只要说明这两个角是 同一个角 的余角(或补角)即可.
·导学建议·
同一个角
互余和互补主要反映的是角的数量关系,而不是角的位置关系.通过合作探究的学习,更好地达成本课时学习目标.
1.下列说法正确的是( A )
A.锐角的补角一定是钝角
B.一个角的补角一定大于这个角
C.锐角和钝角一定互补
D.两个锐角一定互为余角
A
2.如图,∠AOD=∠DOB=∠COE=90°,互补的角有
( C )
A.5对 B.6对 C.7对 D.8对
3.若∠α的补角是它的3倍,则∠α的度数为 45° .
C
45°
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
