【核心素养目标】苏科版八年级数学上册第4章 实数 复习课 课件 (共26张PPT)
文档属性
| 名称 | 【核心素养目标】苏科版八年级数学上册第4章 实数 复习课 课件 (共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 953.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-28 20:25:54 | ||
图片预览








文档简介
(共26张PPT)
第4章 实数
第4章 复习课
1.知道平方根、算术平方根、立方根的概念,能用开平方或开立方运算求一个数的平方根或立方根.
2.知道无理数和实数的概念,会对实数进行分类,能进行简单的实数四则运算.
3.会求实数的绝对值、相反数,会进行实数的大小比较.进一步体会数形结合及分类思想在数学中的重要性.
◎重点:会求一个非负数的平方根、算术平方根及实数的立方根,会进行实数的运算.
◎难点:算术平方根的意义及实数的性质.
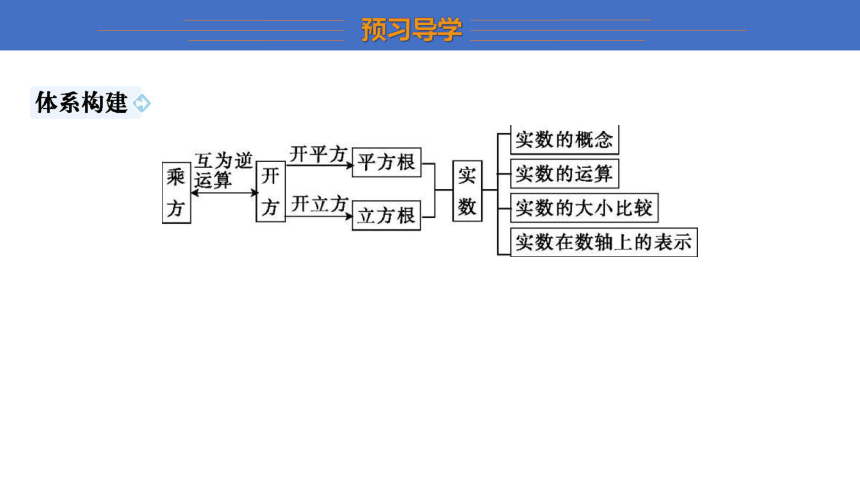
请回顾一下,这一章我们学习了哪些知识.
·导学建议·
本节复习课的主体是知识的再现,可先让学生课前自主复习,回顾这一单元所学知识点,并将自己认为重要的知识点记录整理.
1.结合平方根与算术平方根的概念完成下面的填空.
(1)如果x2=a,那么x(x>0)叫做a的 算术平方根 ,a的算术平方根记作 ,其中a叫做 被开方数 .0的算术平方根是 0 .
(2)如果x2=a,那么x叫做a的 平方根 ,a的平方根记作 ± .
算术平方根
被开方数
0
平方根
±
(3)一个正数有两个平方根,它们 互为相反数 ; 0 的平方根是 0 ,负数 没有平方根 .
(4)求一个数平方根的运算叫做 开平方 ,它与 平方 互为逆运算.
互为相反数
0
没有平方根
开平方
平方
2.立方根的概念和性质.
(1)如果一个数的立方等于a,那么这个数叫做a的 立方 ,记作 ,求一个数立方根的运算叫做 开立方 .
(2)正数的立方根是 正数 ,负数的立方根是 负数 ,0的立方根是 0 .
立方根
开立方
正数
负数
0
3.实数及其运算.
(1) 有理数 和 无理数 统称实数.
(2) 有限 小数和 无限循环 小数叫做有理数, 无限不循环 小数叫做无理数.
(3)实数按大小可分为 正实数 、 0 、 负实数 .
(4)实数与数轴上的点 一一对应 .
(5)数a的相反数是 -a .
有理数
无理数
有限
无限循环
无
限不循环
正实数
0
负实数
一一对应
-a
(6)一个正实数的绝对值是它 本身 ;一个负实数的绝对值是 它的相反数 ; 0的绝对值是 0 .
本身
它的相反数
0
4.你能估计一个无理数的大小吗?
用两端夹值的方法估计无理数的大小.
5.实数比较大小有哪些方法?
(1)数轴比较:对于数轴上的任意两个点,右边的点表示的实数总比左边的点表示的实数大.
(2)符号比较:正实数都大于0,负实数都小于0,正实数大于一切负实数;两个负实数比较大小,绝对值大的反而小.
(3)比较实数大小的方法还有平方法、倒数法、作差法、作商法、估算法、借助中间量比较法等.
·导学建议·
教师通过大屏幕出示问题,学生思考后,回答问题,互相补充完整.或者让学生自己总结所学到的知识并一条一条说出来,其他同学和老师加以补充.
平方根、算术平方根的计算
1.求下列各数的平方根和算术平方根.
(1)2;
解:(1)2的平方根是±,算术平方根是;
(2);
解: (2)的平方根是±,算术平方根是;
(3)1.44.
解: (3)1.44的平方根是±1.2,算术平方根是1.2.
方法归纳交流 一个正数的平方根有 两 个,它们 互为相反数 ,其中 正 的平方根是其算术平方根.
解: (3)1.44的平方根是±1.2,算术平方根是1.2.
两
互
为相反数
正
·导学建议·
问题(2)是学生的易错点,对于出错的学生,可让他们先求的值,再计算.
立方根的计算
2.-0.008和的立方根分别是( C )
A.-0.2,±
B.-0.008无立方根,的立方根为
C.-0.2,
D.±0.2,-
C
方法归纳交流 正数的立方根是 正数 ;负数的立方根是 负数 ;0的立方根是 0 .
正数
负数
0
实数的分类
3.在实数-,0,,-3.14,,,-0.1010010001…(每两个1之间依次多1个0),,这8个实数中,无理数有( C )
A.1个 B.2个
C.3个 D.4个
C
4.下列说法中正确的有 ④⑥ .(填序号)
①无限小数都是无理数;②带根号的数是无理数;③有理数都是有限小数;④实数不是有理数就是无理数;⑤两个无理数的和与积都是无理数;⑥有理数与无理数分别平方后不可能相同.
方法归纳交流 无限不循环 小数是无理数.
④⑥
无限不循环
·导学建议·
可先引导学生回忆无理数、实数的概念及初中阶段常见的几种无理数,然后解决上面的问题.
实数的大小比较与运算
5.已知实数a的相反数是,则a的值为( B )
A. B.-
C.±
B
6.实数a在数轴上的位置如图所示,化简|a-1|+a= 1 .
方法归纳交流 在数轴上,右边的数总比左边的数 大 .
7.在数轴上表示和-的两点间的距离是( C )
A.- -
C.+ D.-(+ )
1
大
C
实数的绝对值、相反数
8.-的相反数是 - ,绝对值是 - .
-
-
9.若+|a+b|=0,则a2020+b2021的值为 0 .
学习小助手
如果两个非负数的和是0,那么这两个数都是 0 .
方法归纳交流 你所知道的非负数有哪些?
实数的绝对值、实数的偶数次方、非负实数的算术平方根等.
0
0
关于几种非负数的问题
·导学建议·
合作探究部分建议用25分钟左右的时间完成.在本节教学中,应该留给学生充分的思考、操作的时间和空间.
第4章 实数
第4章 复习课
1.知道平方根、算术平方根、立方根的概念,能用开平方或开立方运算求一个数的平方根或立方根.
2.知道无理数和实数的概念,会对实数进行分类,能进行简单的实数四则运算.
3.会求实数的绝对值、相反数,会进行实数的大小比较.进一步体会数形结合及分类思想在数学中的重要性.
◎重点:会求一个非负数的平方根、算术平方根及实数的立方根,会进行实数的运算.
◎难点:算术平方根的意义及实数的性质.
请回顾一下,这一章我们学习了哪些知识.
·导学建议·
本节复习课的主体是知识的再现,可先让学生课前自主复习,回顾这一单元所学知识点,并将自己认为重要的知识点记录整理.
1.结合平方根与算术平方根的概念完成下面的填空.
(1)如果x2=a,那么x(x>0)叫做a的 算术平方根 ,a的算术平方根记作 ,其中a叫做 被开方数 .0的算术平方根是 0 .
(2)如果x2=a,那么x叫做a的 平方根 ,a的平方根记作 ± .
算术平方根
被开方数
0
平方根
±
(3)一个正数有两个平方根,它们 互为相反数 ; 0 的平方根是 0 ,负数 没有平方根 .
(4)求一个数平方根的运算叫做 开平方 ,它与 平方 互为逆运算.
互为相反数
0
没有平方根
开平方
平方
2.立方根的概念和性质.
(1)如果一个数的立方等于a,那么这个数叫做a的 立方 ,记作 ,求一个数立方根的运算叫做 开立方 .
(2)正数的立方根是 正数 ,负数的立方根是 负数 ,0的立方根是 0 .
立方根
开立方
正数
负数
0
3.实数及其运算.
(1) 有理数 和 无理数 统称实数.
(2) 有限 小数和 无限循环 小数叫做有理数, 无限不循环 小数叫做无理数.
(3)实数按大小可分为 正实数 、 0 、 负实数 .
(4)实数与数轴上的点 一一对应 .
(5)数a的相反数是 -a .
有理数
无理数
有限
无限循环
无
限不循环
正实数
0
负实数
一一对应
-a
(6)一个正实数的绝对值是它 本身 ;一个负实数的绝对值是 它的相反数 ; 0的绝对值是 0 .
本身
它的相反数
0
4.你能估计一个无理数的大小吗?
用两端夹值的方法估计无理数的大小.
5.实数比较大小有哪些方法?
(1)数轴比较:对于数轴上的任意两个点,右边的点表示的实数总比左边的点表示的实数大.
(2)符号比较:正实数都大于0,负实数都小于0,正实数大于一切负实数;两个负实数比较大小,绝对值大的反而小.
(3)比较实数大小的方法还有平方法、倒数法、作差法、作商法、估算法、借助中间量比较法等.
·导学建议·
教师通过大屏幕出示问题,学生思考后,回答问题,互相补充完整.或者让学生自己总结所学到的知识并一条一条说出来,其他同学和老师加以补充.
平方根、算术平方根的计算
1.求下列各数的平方根和算术平方根.
(1)2;
解:(1)2的平方根是±,算术平方根是;
(2);
解: (2)的平方根是±,算术平方根是;
(3)1.44.
解: (3)1.44的平方根是±1.2,算术平方根是1.2.
方法归纳交流 一个正数的平方根有 两 个,它们 互为相反数 ,其中 正 的平方根是其算术平方根.
解: (3)1.44的平方根是±1.2,算术平方根是1.2.
两
互
为相反数
正
·导学建议·
问题(2)是学生的易错点,对于出错的学生,可让他们先求的值,再计算.
立方根的计算
2.-0.008和的立方根分别是( C )
A.-0.2,±
B.-0.008无立方根,的立方根为
C.-0.2,
D.±0.2,-
C
方法归纳交流 正数的立方根是 正数 ;负数的立方根是 负数 ;0的立方根是 0 .
正数
负数
0
实数的分类
3.在实数-,0,,-3.14,,,-0.1010010001…(每两个1之间依次多1个0),,这8个实数中,无理数有( C )
A.1个 B.2个
C.3个 D.4个
C
4.下列说法中正确的有 ④⑥ .(填序号)
①无限小数都是无理数;②带根号的数是无理数;③有理数都是有限小数;④实数不是有理数就是无理数;⑤两个无理数的和与积都是无理数;⑥有理数与无理数分别平方后不可能相同.
方法归纳交流 无限不循环 小数是无理数.
④⑥
无限不循环
·导学建议·
可先引导学生回忆无理数、实数的概念及初中阶段常见的几种无理数,然后解决上面的问题.
实数的大小比较与运算
5.已知实数a的相反数是,则a的值为( B )
A. B.-
C.±
B
6.实数a在数轴上的位置如图所示,化简|a-1|+a= 1 .
方法归纳交流 在数轴上,右边的数总比左边的数 大 .
7.在数轴上表示和-的两点间的距离是( C )
A.- -
C.+ D.-(+ )
1
大
C
实数的绝对值、相反数
8.-的相反数是 - ,绝对值是 - .
-
-
9.若+|a+b|=0,则a2020+b2021的值为 0 .
学习小助手
如果两个非负数的和是0,那么这两个数都是 0 .
方法归纳交流 你所知道的非负数有哪些?
实数的绝对值、实数的偶数次方、非负实数的算术平方根等.
0
0
关于几种非负数的问题
·导学建议·
合作探究部分建议用25分钟左右的时间完成.在本节教学中,应该留给学生充分的思考、操作的时间和空间.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
