【核心素养目标】苏科版七年级数学上册6.5 垂直 课件(共26张PPT)
文档属性
| 名称 | 【核心素养目标】苏科版七年级数学上册6.5 垂直 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 733.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-28 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
第6章 平面图形的认识(一)
6.5 垂直
1.知道垂线、垂线段、点到直线的距离等概念,会用三角板或量角器过一点画直线的垂线;
2.会运用垂线的定义和性质解决简单的实际问题;
3.经历观察、分析、猜想、概括的学习过程,学会精练、准确地作图.
◎重点:垂线的定义、性质.
◎难点:对点到直线的距离的概念的理解及垂线性质的探究过程.
让学生观察教室里面两条直线相交的情况,有哪些情况,有什么共同特点吗?结合小学学过直角的概念,引入两条直线相交的一种特殊情况——垂直.
垂直的定义
阅读课本本课时第169页第二个“议一议”以上的内容,完成下列问题:
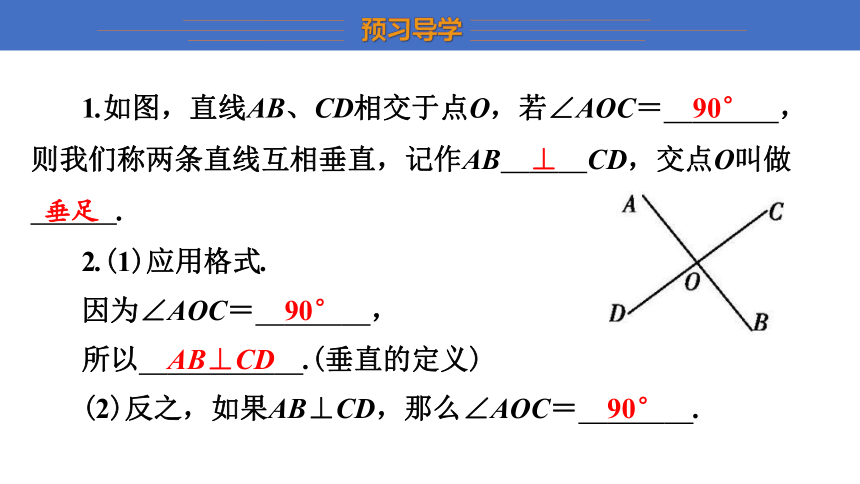
1.如图,直线AB、CD相交于点O,若∠AOC= 90° ,则我们称两条直线互相垂直,记作AB ⊥ CD,交点O叫做 垂足 .
2.(1)应用格式.
因为∠AOC= 90° ,
所以 AB⊥CD .(垂直的定义)
(2)反之,如果AB⊥CD,那么∠AOC= 90° .
90°
⊥
垂足
90°
AB⊥CD
90°
垂线的画法、性质
阅读课本本课时第169页第二个“议一议”到第170页练习前的内容,完成下列问题:(阅读时注意:①画垂线时,应画成直线;②体会“有且只有”的含义)
1.如图1,用三角尺或量角器画直线l的垂线,这样的垂线能画 无数 条.
图略.
2.如图2,在同一平面内,经过直线l上一点A画l的垂线,这样的垂线能画 1 条.
图略.
无数
1
3.如图3,过直线l外一点B画l的垂线,这样的垂线能画 1 条.
图略.
1
4.垂线的画法:过一点画已知直线的垂线,让直角三角板的一直角边与已知直线重合,沿直线左右移动三角板,使其另一直角边经过已知点,沿此直角边画直线,则这条直线就是已知直线的垂线.
归纳总结 在同一平面内,过一点 有且只有一 条直线与已知直线垂直.
有且只有一
学生画垂线时,要强调步骤,用三角板画垂线要做到:一靠二过三画线,老师做好示范,让学生根据步骤画,学生不规范的作图操作要随时纠正.
·导学建议·
垂线段的性质
阅读课本本课时第171页的内容,完成下列问题:(阅读时注意“点到直线的距离”与“点到直线的垂线段”之间的区别与联系)
1.如图,点P与直线l上各点所连接的线段中,线段 PO 最短.
PO
2.测量线段PO的长度,并指出点P到直线l的距离.
测量略,点P到直线l的距离即为线段PO的长度.
归纳总结 1.连接直线外一点与直线上各点的所有线段中, 垂线段 最短.简单说成: 垂线段最短 .
2.直线外一点到这条直线的 垂线段 的长度,叫做点到直线的距离.
垂线段
垂线段最短
垂线段
1.在两条直线相交所成的四个角中,不能判定这两条直线垂直的是( B )
A.对顶角的和为180° B.四个角之和为360°
C.三个角相等 D.有一个直角
B
2.下列各图中,过直线l外的点P画直线l的垂线,用三角尺操作正确的是( C )
C
3. 如图,P是∠AOB的边OB上一点.
(1)过点P画OB的垂线,交OA于点C.
(2)过点P画OA的垂线,垂足为H.
(3)你能否不通过度量比较出PH与PC、CO的长短吗?说明你的理由.
解:(1)(2)所画图形如图所示.
(3)线段PH的长度是点P到直线OA的距离,线段CP的长度是点C到直线OB的距离,根据垂线段最短可得PH<PC<OC.
垂线段的定义
1.若P为直线l外一点,A、B、C为直线l上的不同的点,其中PA=3,PB=4,PC=5,那么点P到直线l的距离( D )
A.小于3 B.等于3
C.大于或等于3 D.小于或等于3
连接直线外一点与直线上各点的所有线段中,什么线段最短?
垂线段最短.
D
变式训练 如图,BC⊥AC,C为垂足,BC=8 cm,AC=6 cm,AB=10 cm,则点B到AC的距离是 8 cm,点A到BC的距离是 6 cm,A、B两点间的距离是 10 cm,点C到AB的距离是 4.8 cm.
8
6
10
4.8
垂线的性质
2.如图,直线AB、CD相交于点O,OE⊥AB,垂足为O,如果∠EOD=42°,那么∠AOC= 48° .
48°
垂线的画法
3.根据语句画图.
(1)过点P画射线AB的垂线,交射线AB的反向延长线于点Q.
(2)过点M画线段CD的垂线,交CD的延长线于点N.
解:如图所示.
解:如图所示.
方法归纳交流 画一条射线或线段的垂线,就是画它们 所在直线 的垂线.
所在直线
垂线段的应用
4.如图,AB是一条河流,要铺设管道将河水引到C,D两个用水点,现有如下两种铺设管道的方案.
方案一:分别过C、D作AB的垂线,垂足为E、F,沿CE、DF铺设管道.
方案二:连接CD交AB于点P,沿PC、PD铺设管道.
这两种铺设管道的方案中哪一种更节省材料?为什么?
解:方案一更节省材料.因为CE⊥AB,所以CE<CP.同理可得DF<DP.所以CE+DF<CP+DP,所以选用方案一更节省材料.
方法归纳交流 此题应用了 垂线段最短 ,不要与“两点之间线段最短”相混淆.
解:方案一更节省材料.因为CE⊥AB,所以CE<CP.同理可
得DF<DP.所以CE+DF<CP+DP,所以选用方案一更节省材
料.
垂线段最短
1. 如图,当∠1与∠2满足条件 ∠1+∠2=90° 时,OA⊥OB.
∠1+∠2=90°
2.如图,OA⊥OB,OC⊥OD,OE是OD的反向延长线.
(1)试说明:∠AOC=∠BOD.
(2)若∠BOD=32°,求∠AOE的度数.
解:(1)因为OA⊥OB,OC⊥OD,
所以∠AOC+∠BOC=90°,
∠BOD+∠BOC=90°,
所以∠AOC=∠BOD(同角的余角相等).
(2)因为OA⊥OB,所以∠AOB=90°,
所以∠AOE=180°-∠AOB-∠BOD=180°-90°-32°=58°.
第6章 平面图形的认识(一)
6.5 垂直
1.知道垂线、垂线段、点到直线的距离等概念,会用三角板或量角器过一点画直线的垂线;
2.会运用垂线的定义和性质解决简单的实际问题;
3.经历观察、分析、猜想、概括的学习过程,学会精练、准确地作图.
◎重点:垂线的定义、性质.
◎难点:对点到直线的距离的概念的理解及垂线性质的探究过程.
让学生观察教室里面两条直线相交的情况,有哪些情况,有什么共同特点吗?结合小学学过直角的概念,引入两条直线相交的一种特殊情况——垂直.
垂直的定义
阅读课本本课时第169页第二个“议一议”以上的内容,完成下列问题:
1.如图,直线AB、CD相交于点O,若∠AOC= 90° ,则我们称两条直线互相垂直,记作AB ⊥ CD,交点O叫做 垂足 .
2.(1)应用格式.
因为∠AOC= 90° ,
所以 AB⊥CD .(垂直的定义)
(2)反之,如果AB⊥CD,那么∠AOC= 90° .
90°
⊥
垂足
90°
AB⊥CD
90°
垂线的画法、性质
阅读课本本课时第169页第二个“议一议”到第170页练习前的内容,完成下列问题:(阅读时注意:①画垂线时,应画成直线;②体会“有且只有”的含义)
1.如图1,用三角尺或量角器画直线l的垂线,这样的垂线能画 无数 条.
图略.
2.如图2,在同一平面内,经过直线l上一点A画l的垂线,这样的垂线能画 1 条.
图略.
无数
1
3.如图3,过直线l外一点B画l的垂线,这样的垂线能画 1 条.
图略.
1
4.垂线的画法:过一点画已知直线的垂线,让直角三角板的一直角边与已知直线重合,沿直线左右移动三角板,使其另一直角边经过已知点,沿此直角边画直线,则这条直线就是已知直线的垂线.
归纳总结 在同一平面内,过一点 有且只有一 条直线与已知直线垂直.
有且只有一
学生画垂线时,要强调步骤,用三角板画垂线要做到:一靠二过三画线,老师做好示范,让学生根据步骤画,学生不规范的作图操作要随时纠正.
·导学建议·
垂线段的性质
阅读课本本课时第171页的内容,完成下列问题:(阅读时注意“点到直线的距离”与“点到直线的垂线段”之间的区别与联系)
1.如图,点P与直线l上各点所连接的线段中,线段 PO 最短.
PO
2.测量线段PO的长度,并指出点P到直线l的距离.
测量略,点P到直线l的距离即为线段PO的长度.
归纳总结 1.连接直线外一点与直线上各点的所有线段中, 垂线段 最短.简单说成: 垂线段最短 .
2.直线外一点到这条直线的 垂线段 的长度,叫做点到直线的距离.
垂线段
垂线段最短
垂线段
1.在两条直线相交所成的四个角中,不能判定这两条直线垂直的是( B )
A.对顶角的和为180° B.四个角之和为360°
C.三个角相等 D.有一个直角
B
2.下列各图中,过直线l外的点P画直线l的垂线,用三角尺操作正确的是( C )
C
3. 如图,P是∠AOB的边OB上一点.
(1)过点P画OB的垂线,交OA于点C.
(2)过点P画OA的垂线,垂足为H.
(3)你能否不通过度量比较出PH与PC、CO的长短吗?说明你的理由.
解:(1)(2)所画图形如图所示.
(3)线段PH的长度是点P到直线OA的距离,线段CP的长度是点C到直线OB的距离,根据垂线段最短可得PH<PC<OC.
垂线段的定义
1.若P为直线l外一点,A、B、C为直线l上的不同的点,其中PA=3,PB=4,PC=5,那么点P到直线l的距离( D )
A.小于3 B.等于3
C.大于或等于3 D.小于或等于3
连接直线外一点与直线上各点的所有线段中,什么线段最短?
垂线段最短.
D
变式训练 如图,BC⊥AC,C为垂足,BC=8 cm,AC=6 cm,AB=10 cm,则点B到AC的距离是 8 cm,点A到BC的距离是 6 cm,A、B两点间的距离是 10 cm,点C到AB的距离是 4.8 cm.
8
6
10
4.8
垂线的性质
2.如图,直线AB、CD相交于点O,OE⊥AB,垂足为O,如果∠EOD=42°,那么∠AOC= 48° .
48°
垂线的画法
3.根据语句画图.
(1)过点P画射线AB的垂线,交射线AB的反向延长线于点Q.
(2)过点M画线段CD的垂线,交CD的延长线于点N.
解:如图所示.
解:如图所示.
方法归纳交流 画一条射线或线段的垂线,就是画它们 所在直线 的垂线.
所在直线
垂线段的应用
4.如图,AB是一条河流,要铺设管道将河水引到C,D两个用水点,现有如下两种铺设管道的方案.
方案一:分别过C、D作AB的垂线,垂足为E、F,沿CE、DF铺设管道.
方案二:连接CD交AB于点P,沿PC、PD铺设管道.
这两种铺设管道的方案中哪一种更节省材料?为什么?
解:方案一更节省材料.因为CE⊥AB,所以CE<CP.同理可得DF<DP.所以CE+DF<CP+DP,所以选用方案一更节省材料.
方法归纳交流 此题应用了 垂线段最短 ,不要与“两点之间线段最短”相混淆.
解:方案一更节省材料.因为CE⊥AB,所以CE<CP.同理可
得DF<DP.所以CE+DF<CP+DP,所以选用方案一更节省材
料.
垂线段最短
1. 如图,当∠1与∠2满足条件 ∠1+∠2=90° 时,OA⊥OB.
∠1+∠2=90°
2.如图,OA⊥OB,OC⊥OD,OE是OD的反向延长线.
(1)试说明:∠AOC=∠BOD.
(2)若∠BOD=32°,求∠AOE的度数.
解:(1)因为OA⊥OB,OC⊥OD,
所以∠AOC+∠BOC=90°,
∠BOD+∠BOC=90°,
所以∠AOC=∠BOD(同角的余角相等).
(2)因为OA⊥OB,所以∠AOB=90°,
所以∠AOE=180°-∠AOB-∠BOD=180°-90°-32°=58°.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
