5.2.3平行线的性质跟踪训练(含详细解析)
文档属性
| 名称 | 5.2.3平行线的性质跟踪训练(含详细解析) |  | |
| 格式 | zip | ||
| 文件大小 | 212.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-24 17:30:22 | ||
图片预览




文档简介
第五章相交线与平行线5.2.3平行线的性质
一.选择题(共8小题)
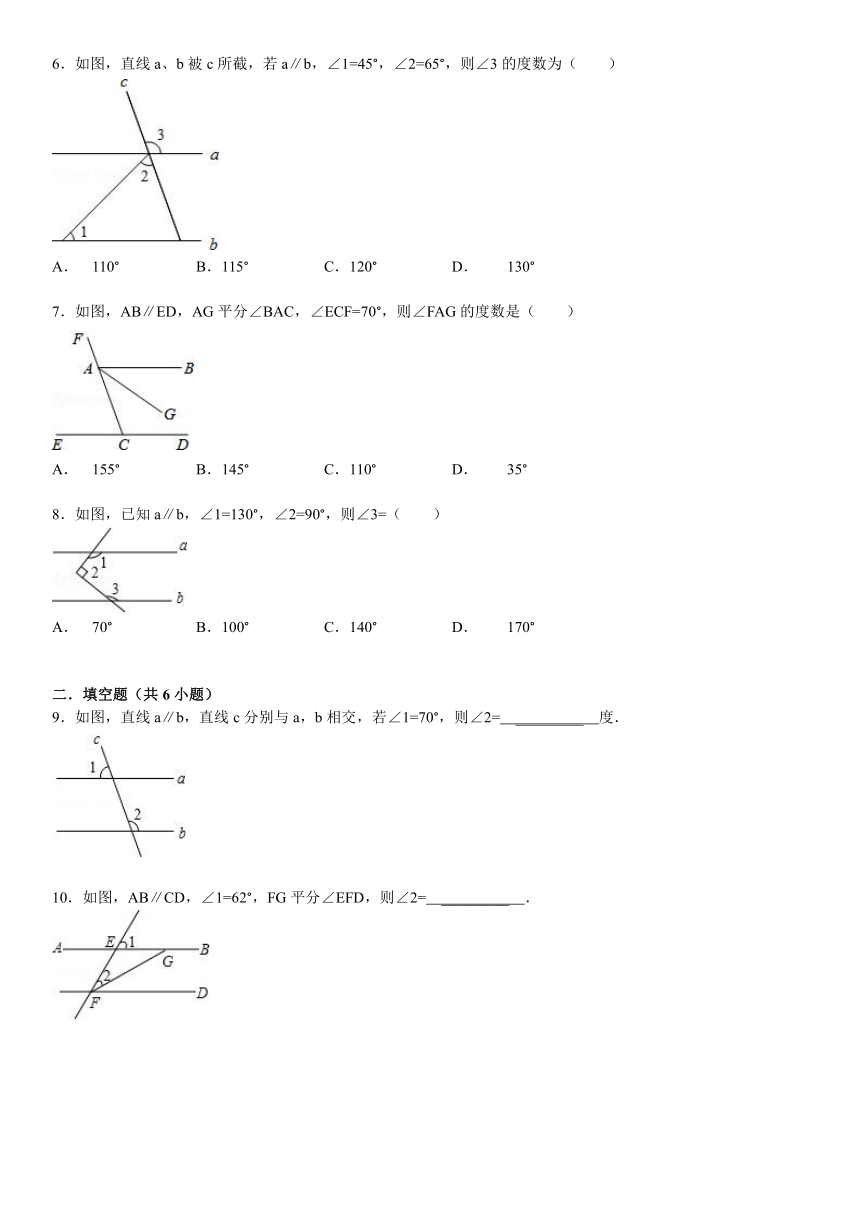
1.将直角三角尺的直角顶点靠在直尺上,且斜边与这根直尺平行,那么,在形成的这个图中与∠α互余的角共有( )
A. 4个 B.3个 C.2个 D. 1个
2.如图,∠A0B的两边0A,0B均为平面反光镜,∠A0B=40°.在射线0B上有一点P,从P点射出一束光线经0A上的Q点反射后,反射光线QR恰好与0B平行,则∠QPB的度数是( )
A. 60° B.80° C.100° D. 120°
3.如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
A. 15° B.20° C.25° D. 30°
4.如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C为( )
A. 30° B.60° C.80° D. 120°
5.如图,CF是△ABC的外角∠ACM的平分线,且CF∥AB,∠ACF=50°,则∠B的度数为( )
A. 80° B.40° C.60° D. 50°
6.如图,直线a、b被c所截,若a∥b,∠1=45°,∠2=65°,则∠3的度数为( )
A. 110° B.115° C.120° D. 130°
7.如图,AB∥ED,AG平分∠BAC,∠ECF=70°,则∠FAG的度数是( )
A. 155° B.145° C.110° D. 35°
8.如图,已知a∥b,∠1=130°,∠2=90°,则∠3=( )
A. 70° B.100° C.140° D. 170°
二.填空题(共6小题)
9.如图,直线a∥b,直线c分别与a,b相交,若∠1=70°,则∠2= _________ 度.
10.如图,AB∥CD,∠1=62°,FG平分∠EFD,则∠2= _________ .
11.如图,直线AB,CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3= _________ 度.
12.如图,已知a∥b,小亮把三角板的直角顶点放在直线b上.若∠1=35°,则∠2的度数为 _________ .
13.如图,直线a∥b,直线l与a相交于点P,与直线b相交于点Q,PM⊥l于点P,若∠1=50°,则∠2= _________ °.
14.如图,直线a、b被第三条直线c所截,如果a∥b,∠1=70°,那么∠3的度数是 _________ .
三.解答题(共10小题)
15.如图,EF∥BC,AC平分∠BAF,∠B=80°.求∠C的度数.
16.如图,直线a∥b,点B在直线上b上,且AB⊥BC,∠1=55°,求∠2的度数.
17.如图,AB∥CD,∠A=75°,∠C=30°,求∠E的度数.
18.如图,已知∠ABD=40°,∠ADB=65°,AB∥DC,求∠ADC的度数.
19.如图,一条铁路修到一个村子边时,需拐弯绕道而过,如果第一次拐的角∠A是105度,第二次拐的角∠B是135度,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,那么∠C应为多少度?
20.如图,∠B=40°,CD∥AB,AC平分∠BCD,求∠A的度数.
21.如图,已知AB∥DE,∠A=40°,∠ACD=100°,求∠D的度数.
22.如图,已知直线m∥n,∠1=105°,2=140°,求∠3的大小.
23.已知AB⊥BC,BE∥CF,∠1=∠2,试说明CD⊥BC.
24.如图,已知AB∥CD,∠B=∠D=120°,求∠BOD的度数.
第五章相交线与平行线5.2.3平行线的性质
参考答案与试题解析
一.选择题(共8小题)
1.将直角三角尺的直角顶点靠在直尺上,且斜边与这根直尺平行,那么,在形成的这个图中与∠α互余的角共有( )
A. 4个 B.3个 C.2个 D. 1个
考点: 平行线的性质;余角和补角.
专题: 几何图形问题.
分析: 由互余的定义、平行线的性质,利用等量代换求解即可.
解答: 解:∵斜边与这根直尺平行,
∴∠α=∠2,
又∵∠1+∠2=90°,
∴∠1+∠α=90°,
又∠α+∠3=90°
∴与α互余的角为∠1和∠3.
故选:C.
点评: 此题考查的是对平行线的性质的理解,目的是找出与∠α和为90°的角.
2.如图,∠A0B的两边0A,0B均为平面反光镜,∠A0B=40°.在射线0B上有一点P,从P点射出一束光线经0A上的Q点反射后,反射光线QR恰好与0B平行,则∠QPB的度数是( )
A. 60° B.80° C 100° D. 120°
考点: 平行线的性质.
专题: 几何图形问题.
分析: 根据两直线平行,同位角相等、同旁内角互补以及平角的定义可计算即可.
解答: 解:∵QR∥OB,∴∠AQR=∠AOB=40°,∠PQR+∠QPB=180°;
∵∠AQR=∠PQO,∠AQR+∠PQO+∠RQP=180°(平角定义),
∴∠PQR=180°﹣2∠AQR=100°,
∴∠QPB=180°﹣100°=80°.
故选:B.
点评: 本题结合反射现象,考查了平行线的性质和平角的定义,是一道好题.
3.如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
A. 15° B.20° C.25° D. 30°
考点: 平行线的性质.
专题: 压轴题.
分析: 根据两直线平行,内错角相等求出∠3,再求解即可.
解答: 解:∵直尺的两边平行,∠1=20°,
∴∠3=∠1=20°,
∴∠2=45°﹣20°=25°.
故选:C.
点评: 本题考查了两直线平行,内错角相等的性质,熟记性质是解题的关键.
4.如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C为( )
A. 30° B.60° C.80° D. 120°
考点: 平行线的性质;角平分线的性质.
分析: 根据两直线平行,同位角相等可得∠EAD=∠B,再根据角平分线的定义求出∠EAC,然后根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
解答: 解:∵AD∥BC,∠B=30°,
∴∠EAD=∠B=30°,
∵AD是∠EAC的平分线,
∴∠EAC=2∠EAD=2×30°=60°,
∴∠C=∠EAC﹣∠B=60°﹣30°=30°.
故选:A.
点评: 本题考查了平行线的性质,角平分线的定义,以及三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质是解题的关键.
5.如图,CF是△ABC的外角∠ACM的平分线,且CF∥AB,∠ACF=50°,则∠B的度数为( )
A. 80° B.40° C.60° D. 50°
考点: 平行线的性质.
分析: 根据角平分线的定义可得∠FCM=∠ACF,再根据两直线平行,同位角相等可得∠B=∠FCM.
解答: 解:∵CF是∠ACM的平分线,
∴∠FCM=∠ACF=50°,
∵CF∥AB,
∴∠B=∠FCM=50°.
故选:D.
点评: 本题考查了平行线的性质,角平分线的定义,是基础题,熟记性质并准确识图是解题的关键.
6.如图,直线a、b被c所截,若a∥b,∠1=45°,∠2=65°,则∠3的度数为( )
A. 110° B 115° C.120° D. 130°
考点: 平行线的性质;三角形的外角性质.
分析: 首先根据三角形的外角性质得到∠1+∠2=∠4,然后根据平行线的性质得到∠3=∠4求解.
解答: 解:根据三角形的外角性质,
∴∠1+∠2=∠4=110°,
∵a∥b,
∴∠3=∠4=110°,
故选:A.
点评: 本题考查了平行线的性质以及三角形的外角性质,属于基础题,难度较小.
7.如图,AB∥ED,AG平分∠BAC,∠ECF=70°,则∠FAG的度数是( )
A. 155° B. 145° C. 110° D. 35°
考点: 平行线的性质.
专题: 计算题.
分析: 首先,由平行线的性质得到∠BAC=∠ECF=70°;然后利用邻补角的定义、角平分线的定义来求∠FAG的度数.
解答: 解:如图,∵AB∥ED,∠ECF=70°,
∴∠BAC=∠ECF=70°,
∴∠FAB=180°﹣∠BAC=110°.
又∵AG平分∠BAC,
∴∠BAG=∠BAC=35°,
∴∠FAG=∠FAB+∠BAG=145°.
故选:B.
点评: 本题考查了平行线的性质.根据“两直线平行,内错角相等”求得∠BAC的度数是解题的难点.
8.如图,已知a∥b,∠1=130°,∠2=90°,则∠3=( )
A. 70° B. 100° C. 140° D. 170°
考点: 平行线的性质.
分析: 延长∠1的边与直线b相交,然后根据两直线平行,同旁内角互补求出∠4,再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
解答: 解:如图,延长∠1的边与直线b相交,
∵a∥b,
∴∠4=180°﹣∠1=180°﹣130°=50°,
由三角形的外角性质,∠3=∠2+∠4=90°+50°=140°.
故选:C.
点评: 本题考查了平行线的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质并作出辅助线是解题的关键.
二.填空题(共6小题)
9.如图,直线a∥b,直线c分别与a,b相交,若∠1=70°,则∠2= 110 度.
考点: 平行线的性质;对顶角、邻补角.
专题: 计算题.
分析: 直线a∥b,直线c分别与a,b相交,根据平行线的性质,以及对顶角的定义可求出.
解答: 解:∵∠1=70°,
∴∠3=∠1=70°,
∵a∥b,
∴∠2+∠3=180°,
∴∠2=180°﹣70°=110°.
故答案为:110.
点评: 本题考查两直线平行,同位角相等及邻补角互补.
10.如图,AB∥CD,∠1=62°,FG平分∠EFD,则∠2= 31° .
考点: 平行线的性质.
分析: 根据两直线平行,同位角相等可得∠EFD=∠1,再根据角平分线的定义可得∠2=∠EFD.
解答: 解:∵AB∥CD,
∴∠EFD=∠1=62°,
∵FG平分∠EFD,
∴∠2=∠EFD=×62°=31°.
故答案为:31°.
点评: 本题考查了平行线的性质,角平分线的定义,是基础题,熟记性质是解题的关键.
11.如图,直线AB,CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3= 80 度.
考点: 平行线的性质.
专题: 计算题.
分析: 根据平行线的性质求出∠C,根据三角形外角性质求出即可.
解答: 解:∵AB∥CD,∠1=45°,
∴∠C=∠1=45°,
∵∠2=35°,
∴∠3=∠∠2+∠C=35°+45°=80°,
故答案为:80.
点评: 本题考查了平行线的性质,三角形的外角性质的应用,解此题的关键是求出∠C的度数和得出∠3=∠2+∠C.
12.如图,已知a∥b,小亮把三角板的直角顶点放在直线b上.若∠1=35°,则∠2的度数为 55° .
考点: 平行线的性质;余角和补角.
分析: 先根据三角板的直角顶点在直线b上求出∠3的度数,再由平行线的性质即可得出结论.
解答: 解:∵三角板的直角顶点在直线b上,∠1=35°,
∵a∥b,
∴∠3=∠1=35°,
∴∠4=90°﹣∠3=55°,
∴∠2=∠3=55°.
故答案为:55°.
点评: 本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等.
13.如图,直线a∥b,直线l与a相交于点P,与直线b相交于点Q,PM⊥l于点P,若∠1=50°,则∠2= 40 °.
考点: 平行线的性质;垂线.
专题: 计算题.
分析: 根据两直线平行,内错角相等,即可求得∠3=∠1,根据PM⊥l于点P,则∠MPQ=90°,即可求解.
解答: 解:∵直线a∥b,
∴∠3=∠1=50°,
又∵PM⊥l于点P,
∴∠MPQ=90°,
∴∠2=90°﹣∠3=90°﹣50°=40°.
故答案是:40.
点评: 本题重点考查了平行线的性质及垂直的定义,是一道较为简单的题目.
14.如图,直线a、b被第三条直线c所截,如果a∥b,∠1=70°,那么∠3的度数是 70° .
考点: 平行线的性质.
分析: 根据两直线平行,同位角相等可得∠2=∠1,再根据对顶角相等可得∠3=∠2.
解答: 解:∵a∥b,
∴∠2=∠1=70°,
∴∠3=∠2=70°.
故答案为:70°.
点评: 本题考查了平行线的性质,对顶角相等的性质,熟记性质是解题的关键.
三.解答题(共10小题)
15.如图,EF∥BC,AC平分∠BAF,∠B=80°.求∠C的度数.
考点: 平行线的性质.
分析: 根据两直线平行,同旁内角互补求出∠BAF,再根据角平分线的定义求出∠CAF,然后根据两直线平行,内错角相等解答.
解答: 解:∵EF∥BC,
∴∠BAF=180°﹣∠B=100°,
∵AC平分∠BAF,
∴∠CAF=∠BAF=50°,
∵EF∥BC,
∴∠C=∠CAF=50°.
点评: 本题考查了平行线的性质,角平分线的定义,熟记性质并准确识图是解题的关键.
16.如图,直线a∥b,点B在直线上b上,且AB⊥BC,∠1=55°,求∠2的度数.
考点: 平行线的性质.
分析: 根据垂直定义和邻补角求出∠3,根据平行线的性质得出∠2=∠3,代入求出即可.
解答: 解:
∵AB⊥BC,
∴∠ABC=90°,
∴∠1+∠3=90°,
∵∠1=55°,
∴∠3=35°,
∵a∥b,
∴∠2=∠3=35°.
点评: 本题考查了垂直定义,平行线的性质的应用,注意:两直线平行,同位角相等.
17.如图,AB∥CD,∠A=75°,∠C=30°,求∠E的度数.
考点: 平行线的性质.
分析: 由AB∥CD,∠A=75°,根据两直线平行,同位角相等,即可求得∠1的度数,又由三角形外角的性质,即可求得∠E的度数.
解答: 解:∵AB∥CD,∠A=75°,
∴∠1=∠A=75°,
∵∠C=30°,
∴∠E=∠1﹣∠C=75°﹣30°=45°.
点评: 此题考查了平行线的性质与三角形外角的性质.此题难度不大,注意掌握数形结合思想的应用.
18.如图,已知∠ABD=40°,∠ADB=65°,AB∥DC,求∠ADC的度数.
考点: 平行线的性质.
分析: 由AB与DC平行,利用两直线平行得到一对内错角相等,由∠ADB+∠BDC求出∠ADC度数.
解答: 解:∵AB∥DC
∴∠BDC=∠ABD=40°,
∵∠ADB=65°,
∴∠ADC=∠ADB+∠BDC=105°.
点评: 此题考查了平行线的性质,熟练掌握平行线的性质是解本题的关键.
19.如图,一条铁路修到一个村子边时,需拐弯绕道而过,如果第一次拐的角∠A是105度,第二次拐的角∠B是135度,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,那么∠C应为多少度?
考点: 平行线的性质.
专题: 应用题.
分析: 过点B作直线BE∥CD,用“两直线平行内错角相等”和“两直线平行同旁内角互补”解答.
解答: 解:过点B作直线BE∥CD.
∵CD∥AF,
∴BE∥CD∥AF.
∴∠A=∠ABE=105°.
∴∠CBE=∠ABC﹣∠ABE=30°.
又∵BE∥CD,
∴∠CBE+∠C=180°.
∴∠C=150°.
点评: 此题是一道生活实际问题,根据题目信息,转化为关于平行线性质的数学问题.
20.如图,∠B=40°,CD∥AB,AC平分∠BCD,求∠A的度数.
考点: 平行线的性质.
分析: 先根据两直线平行,同旁内角互补求出∠BCD的度数,然后根据角平分线的定义求出∠ACD的度数,再根据两直线平行,内错角相等求解.
解答: 解:∵CD∥AB,∠B=40°,
∴∠DCE=40°,
∴∠BCD=180°﹣40°=140°,
∵AC平分∠BCD,
∴∠ACD=×140°=70°,
∴∠A=∠ACD=70°.
点评: 本题主要考查了两直线平行,同旁内角互补,两直线平行,内错角相等的性质,角平分线的定义,解题关键在于准确识图,找准各种位置关系的角.
21.如图,已知AB∥DE,∠A=40°,∠ACD=100°,求∠D的度数.
考点: 平行线的性质.
分析: 首先过C作CF∥AB,再证明AB∥FC∥DE,根据平行线的性质可得∠A=∠ACF=40°,∠D=∠FCD,进而得到答案.
解答: 解:过C作CF∥AB,
∵AB∥DE,
∴AB∥FC∥DE,
∴∠A=∠ACF=40°,∠D=∠FCD,
∵∠ACD=100°,
∴∠FCD=100°﹣40°=60°,
∴∠D=60°.
点评: 此题主要考查了平行线的性质,关键是掌握两直线平行,内错角相等.
22.如图,已知直线m∥n,∠1=105°,2=140°,求∠3的大小.
考点: 平行线的性质.
分析: 作直线l∥m∥n,然后根据平行线的性质可得∠1+∠4=180°,∠2+∠5=180°,根据已知求出∠4+∠5的度数,然后根据邻补角的知识求得∠3的度数.
解答: 解:作直线l∥m∥n,
∴∠1+∠4=180°,∠2+∠5=180°,
∵∠1=105°,2=140°,
∴∠4=75°,∠5=40°,
∵∠3为∠4+∠5的邻补角,
∴∠3=180°﹣75°﹣40°=65°.
点评: 本题考查了平行线的性质,关键是作出辅助线,注意掌握平行线的性质:两直线平行,同旁内角互补.
23.已知AB⊥BC,BE∥CF,∠1=∠2,试说明CD⊥BC.
考点: 平行线的性质;垂线.
专题: 证明题.
分析: 先根据垂线的定义得到∠1+∠EBC=90°,再根据平行线的性质得∠EBC=∠FCB,则∠2+∠FCB=∠1+∠EBC=90°,然后根据垂线的定义即可得到结论.
解答: 证明:∵AB⊥BC,
∴∠1+∠EBC=90°,
∵BE∥CF,
∴∠EBC=∠FCB,
∵∠1=∠2,
∴∠2+∠FCB=∠1+∠EBC=90°,
∴CD⊥BC.
点评: 本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.也考查了垂线的定义.
24.如图,已知AB∥CD,∠B=∠D=120°,求∠BOD的度数.
考点: 平行线的性质.
专题: 计算题.
分析: 过O作OE平行于AB,由AB与CD平行,得到OE与CD平行,利用两直线平行同旁内角互补得到两对角互补,由∠B=∠D=120°,求出∠BOE与∠EOD的度数,相加即可确定出∠BOD度数.
解答: 解:过O作OE∥AB,
∵AB∥CD,
∴OE∥CD,
∴∠BOE+∠B=180°,∠EOD+∠D=180°,
∵∠B=∠D=120°,
∴∠BOE=∠EOD=60°,
则∠BOD=∠BOE+∠EOD=120°.
点评: 此题考查了平行线的性质,熟练掌握平行线的性质是解本题的关键.
一.选择题(共8小题)
1.将直角三角尺的直角顶点靠在直尺上,且斜边与这根直尺平行,那么,在形成的这个图中与∠α互余的角共有( )
A. 4个 B.3个 C.2个 D. 1个
2.如图,∠A0B的两边0A,0B均为平面反光镜,∠A0B=40°.在射线0B上有一点P,从P点射出一束光线经0A上的Q点反射后,反射光线QR恰好与0B平行,则∠QPB的度数是( )
A. 60° B.80° C.100° D. 120°
3.如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
A. 15° B.20° C.25° D. 30°
4.如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C为( )
A. 30° B.60° C.80° D. 120°
5.如图,CF是△ABC的外角∠ACM的平分线,且CF∥AB,∠ACF=50°,则∠B的度数为( )
A. 80° B.40° C.60° D. 50°
6.如图,直线a、b被c所截,若a∥b,∠1=45°,∠2=65°,则∠3的度数为( )
A. 110° B.115° C.120° D. 130°
7.如图,AB∥ED,AG平分∠BAC,∠ECF=70°,则∠FAG的度数是( )
A. 155° B.145° C.110° D. 35°
8.如图,已知a∥b,∠1=130°,∠2=90°,则∠3=( )
A. 70° B.100° C.140° D. 170°
二.填空题(共6小题)
9.如图,直线a∥b,直线c分别与a,b相交,若∠1=70°,则∠2= _________ 度.
10.如图,AB∥CD,∠1=62°,FG平分∠EFD,则∠2= _________ .
11.如图,直线AB,CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3= _________ 度.
12.如图,已知a∥b,小亮把三角板的直角顶点放在直线b上.若∠1=35°,则∠2的度数为 _________ .
13.如图,直线a∥b,直线l与a相交于点P,与直线b相交于点Q,PM⊥l于点P,若∠1=50°,则∠2= _________ °.
14.如图,直线a、b被第三条直线c所截,如果a∥b,∠1=70°,那么∠3的度数是 _________ .
三.解答题(共10小题)
15.如图,EF∥BC,AC平分∠BAF,∠B=80°.求∠C的度数.
16.如图,直线a∥b,点B在直线上b上,且AB⊥BC,∠1=55°,求∠2的度数.
17.如图,AB∥CD,∠A=75°,∠C=30°,求∠E的度数.
18.如图,已知∠ABD=40°,∠ADB=65°,AB∥DC,求∠ADC的度数.
19.如图,一条铁路修到一个村子边时,需拐弯绕道而过,如果第一次拐的角∠A是105度,第二次拐的角∠B是135度,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,那么∠C应为多少度?
20.如图,∠B=40°,CD∥AB,AC平分∠BCD,求∠A的度数.
21.如图,已知AB∥DE,∠A=40°,∠ACD=100°,求∠D的度数.
22.如图,已知直线m∥n,∠1=105°,2=140°,求∠3的大小.
23.已知AB⊥BC,BE∥CF,∠1=∠2,试说明CD⊥BC.
24.如图,已知AB∥CD,∠B=∠D=120°,求∠BOD的度数.
第五章相交线与平行线5.2.3平行线的性质
参考答案与试题解析
一.选择题(共8小题)
1.将直角三角尺的直角顶点靠在直尺上,且斜边与这根直尺平行,那么,在形成的这个图中与∠α互余的角共有( )
A. 4个 B.3个 C.2个 D. 1个
考点: 平行线的性质;余角和补角.
专题: 几何图形问题.
分析: 由互余的定义、平行线的性质,利用等量代换求解即可.
解答: 解:∵斜边与这根直尺平行,
∴∠α=∠2,
又∵∠1+∠2=90°,
∴∠1+∠α=90°,
又∠α+∠3=90°
∴与α互余的角为∠1和∠3.
故选:C.
点评: 此题考查的是对平行线的性质的理解,目的是找出与∠α和为90°的角.
2.如图,∠A0B的两边0A,0B均为平面反光镜,∠A0B=40°.在射线0B上有一点P,从P点射出一束光线经0A上的Q点反射后,反射光线QR恰好与0B平行,则∠QPB的度数是( )
A. 60° B.80° C 100° D. 120°
考点: 平行线的性质.
专题: 几何图形问题.
分析: 根据两直线平行,同位角相等、同旁内角互补以及平角的定义可计算即可.
解答: 解:∵QR∥OB,∴∠AQR=∠AOB=40°,∠PQR+∠QPB=180°;
∵∠AQR=∠PQO,∠AQR+∠PQO+∠RQP=180°(平角定义),
∴∠PQR=180°﹣2∠AQR=100°,
∴∠QPB=180°﹣100°=80°.
故选:B.
点评: 本题结合反射现象,考查了平行线的性质和平角的定义,是一道好题.
3.如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
A. 15° B.20° C.25° D. 30°
考点: 平行线的性质.
专题: 压轴题.
分析: 根据两直线平行,内错角相等求出∠3,再求解即可.
解答: 解:∵直尺的两边平行,∠1=20°,
∴∠3=∠1=20°,
∴∠2=45°﹣20°=25°.
故选:C.
点评: 本题考查了两直线平行,内错角相等的性质,熟记性质是解题的关键.
4.如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C为( )
A. 30° B.60° C.80° D. 120°
考点: 平行线的性质;角平分线的性质.
分析: 根据两直线平行,同位角相等可得∠EAD=∠B,再根据角平分线的定义求出∠EAC,然后根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
解答: 解:∵AD∥BC,∠B=30°,
∴∠EAD=∠B=30°,
∵AD是∠EAC的平分线,
∴∠EAC=2∠EAD=2×30°=60°,
∴∠C=∠EAC﹣∠B=60°﹣30°=30°.
故选:A.
点评: 本题考查了平行线的性质,角平分线的定义,以及三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质是解题的关键.
5.如图,CF是△ABC的外角∠ACM的平分线,且CF∥AB,∠ACF=50°,则∠B的度数为( )
A. 80° B.40° C.60° D. 50°
考点: 平行线的性质.
分析: 根据角平分线的定义可得∠FCM=∠ACF,再根据两直线平行,同位角相等可得∠B=∠FCM.
解答: 解:∵CF是∠ACM的平分线,
∴∠FCM=∠ACF=50°,
∵CF∥AB,
∴∠B=∠FCM=50°.
故选:D.
点评: 本题考查了平行线的性质,角平分线的定义,是基础题,熟记性质并准确识图是解题的关键.
6.如图,直线a、b被c所截,若a∥b,∠1=45°,∠2=65°,则∠3的度数为( )
A. 110° B 115° C.120° D. 130°
考点: 平行线的性质;三角形的外角性质.
分析: 首先根据三角形的外角性质得到∠1+∠2=∠4,然后根据平行线的性质得到∠3=∠4求解.
解答: 解:根据三角形的外角性质,
∴∠1+∠2=∠4=110°,
∵a∥b,
∴∠3=∠4=110°,
故选:A.
点评: 本题考查了平行线的性质以及三角形的外角性质,属于基础题,难度较小.
7.如图,AB∥ED,AG平分∠BAC,∠ECF=70°,则∠FAG的度数是( )
A. 155° B. 145° C. 110° D. 35°
考点: 平行线的性质.
专题: 计算题.
分析: 首先,由平行线的性质得到∠BAC=∠ECF=70°;然后利用邻补角的定义、角平分线的定义来求∠FAG的度数.
解答: 解:如图,∵AB∥ED,∠ECF=70°,
∴∠BAC=∠ECF=70°,
∴∠FAB=180°﹣∠BAC=110°.
又∵AG平分∠BAC,
∴∠BAG=∠BAC=35°,
∴∠FAG=∠FAB+∠BAG=145°.
故选:B.
点评: 本题考查了平行线的性质.根据“两直线平行,内错角相等”求得∠BAC的度数是解题的难点.
8.如图,已知a∥b,∠1=130°,∠2=90°,则∠3=( )
A. 70° B. 100° C. 140° D. 170°
考点: 平行线的性质.
分析: 延长∠1的边与直线b相交,然后根据两直线平行,同旁内角互补求出∠4,再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
解答: 解:如图,延长∠1的边与直线b相交,
∵a∥b,
∴∠4=180°﹣∠1=180°﹣130°=50°,
由三角形的外角性质,∠3=∠2+∠4=90°+50°=140°.
故选:C.
点评: 本题考查了平行线的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质并作出辅助线是解题的关键.
二.填空题(共6小题)
9.如图,直线a∥b,直线c分别与a,b相交,若∠1=70°,则∠2= 110 度.
考点: 平行线的性质;对顶角、邻补角.
专题: 计算题.
分析: 直线a∥b,直线c分别与a,b相交,根据平行线的性质,以及对顶角的定义可求出.
解答: 解:∵∠1=70°,
∴∠3=∠1=70°,
∵a∥b,
∴∠2+∠3=180°,
∴∠2=180°﹣70°=110°.
故答案为:110.
点评: 本题考查两直线平行,同位角相等及邻补角互补.
10.如图,AB∥CD,∠1=62°,FG平分∠EFD,则∠2= 31° .
考点: 平行线的性质.
分析: 根据两直线平行,同位角相等可得∠EFD=∠1,再根据角平分线的定义可得∠2=∠EFD.
解答: 解:∵AB∥CD,
∴∠EFD=∠1=62°,
∵FG平分∠EFD,
∴∠2=∠EFD=×62°=31°.
故答案为:31°.
点评: 本题考查了平行线的性质,角平分线的定义,是基础题,熟记性质是解题的关键.
11.如图,直线AB,CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3= 80 度.
考点: 平行线的性质.
专题: 计算题.
分析: 根据平行线的性质求出∠C,根据三角形外角性质求出即可.
解答: 解:∵AB∥CD,∠1=45°,
∴∠C=∠1=45°,
∵∠2=35°,
∴∠3=∠∠2+∠C=35°+45°=80°,
故答案为:80.
点评: 本题考查了平行线的性质,三角形的外角性质的应用,解此题的关键是求出∠C的度数和得出∠3=∠2+∠C.
12.如图,已知a∥b,小亮把三角板的直角顶点放在直线b上.若∠1=35°,则∠2的度数为 55° .
考点: 平行线的性质;余角和补角.
分析: 先根据三角板的直角顶点在直线b上求出∠3的度数,再由平行线的性质即可得出结论.
解答: 解:∵三角板的直角顶点在直线b上,∠1=35°,
∵a∥b,
∴∠3=∠1=35°,
∴∠4=90°﹣∠3=55°,
∴∠2=∠3=55°.
故答案为:55°.
点评: 本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等.
13.如图,直线a∥b,直线l与a相交于点P,与直线b相交于点Q,PM⊥l于点P,若∠1=50°,则∠2= 40 °.
考点: 平行线的性质;垂线.
专题: 计算题.
分析: 根据两直线平行,内错角相等,即可求得∠3=∠1,根据PM⊥l于点P,则∠MPQ=90°,即可求解.
解答: 解:∵直线a∥b,
∴∠3=∠1=50°,
又∵PM⊥l于点P,
∴∠MPQ=90°,
∴∠2=90°﹣∠3=90°﹣50°=40°.
故答案是:40.
点评: 本题重点考查了平行线的性质及垂直的定义,是一道较为简单的题目.
14.如图,直线a、b被第三条直线c所截,如果a∥b,∠1=70°,那么∠3的度数是 70° .
考点: 平行线的性质.
分析: 根据两直线平行,同位角相等可得∠2=∠1,再根据对顶角相等可得∠3=∠2.
解答: 解:∵a∥b,
∴∠2=∠1=70°,
∴∠3=∠2=70°.
故答案为:70°.
点评: 本题考查了平行线的性质,对顶角相等的性质,熟记性质是解题的关键.
三.解答题(共10小题)
15.如图,EF∥BC,AC平分∠BAF,∠B=80°.求∠C的度数.
考点: 平行线的性质.
分析: 根据两直线平行,同旁内角互补求出∠BAF,再根据角平分线的定义求出∠CAF,然后根据两直线平行,内错角相等解答.
解答: 解:∵EF∥BC,
∴∠BAF=180°﹣∠B=100°,
∵AC平分∠BAF,
∴∠CAF=∠BAF=50°,
∵EF∥BC,
∴∠C=∠CAF=50°.
点评: 本题考查了平行线的性质,角平分线的定义,熟记性质并准确识图是解题的关键.
16.如图,直线a∥b,点B在直线上b上,且AB⊥BC,∠1=55°,求∠2的度数.
考点: 平行线的性质.
分析: 根据垂直定义和邻补角求出∠3,根据平行线的性质得出∠2=∠3,代入求出即可.
解答: 解:
∵AB⊥BC,
∴∠ABC=90°,
∴∠1+∠3=90°,
∵∠1=55°,
∴∠3=35°,
∵a∥b,
∴∠2=∠3=35°.
点评: 本题考查了垂直定义,平行线的性质的应用,注意:两直线平行,同位角相等.
17.如图,AB∥CD,∠A=75°,∠C=30°,求∠E的度数.
考点: 平行线的性质.
分析: 由AB∥CD,∠A=75°,根据两直线平行,同位角相等,即可求得∠1的度数,又由三角形外角的性质,即可求得∠E的度数.
解答: 解:∵AB∥CD,∠A=75°,
∴∠1=∠A=75°,
∵∠C=30°,
∴∠E=∠1﹣∠C=75°﹣30°=45°.
点评: 此题考查了平行线的性质与三角形外角的性质.此题难度不大,注意掌握数形结合思想的应用.
18.如图,已知∠ABD=40°,∠ADB=65°,AB∥DC,求∠ADC的度数.
考点: 平行线的性质.
分析: 由AB与DC平行,利用两直线平行得到一对内错角相等,由∠ADB+∠BDC求出∠ADC度数.
解答: 解:∵AB∥DC
∴∠BDC=∠ABD=40°,
∵∠ADB=65°,
∴∠ADC=∠ADB+∠BDC=105°.
点评: 此题考查了平行线的性质,熟练掌握平行线的性质是解本题的关键.
19.如图,一条铁路修到一个村子边时,需拐弯绕道而过,如果第一次拐的角∠A是105度,第二次拐的角∠B是135度,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,那么∠C应为多少度?
考点: 平行线的性质.
专题: 应用题.
分析: 过点B作直线BE∥CD,用“两直线平行内错角相等”和“两直线平行同旁内角互补”解答.
解答: 解:过点B作直线BE∥CD.
∵CD∥AF,
∴BE∥CD∥AF.
∴∠A=∠ABE=105°.
∴∠CBE=∠ABC﹣∠ABE=30°.
又∵BE∥CD,
∴∠CBE+∠C=180°.
∴∠C=150°.
点评: 此题是一道生活实际问题,根据题目信息,转化为关于平行线性质的数学问题.
20.如图,∠B=40°,CD∥AB,AC平分∠BCD,求∠A的度数.
考点: 平行线的性质.
分析: 先根据两直线平行,同旁内角互补求出∠BCD的度数,然后根据角平分线的定义求出∠ACD的度数,再根据两直线平行,内错角相等求解.
解答: 解:∵CD∥AB,∠B=40°,
∴∠DCE=40°,
∴∠BCD=180°﹣40°=140°,
∵AC平分∠BCD,
∴∠ACD=×140°=70°,
∴∠A=∠ACD=70°.
点评: 本题主要考查了两直线平行,同旁内角互补,两直线平行,内错角相等的性质,角平分线的定义,解题关键在于准确识图,找准各种位置关系的角.
21.如图,已知AB∥DE,∠A=40°,∠ACD=100°,求∠D的度数.
考点: 平行线的性质.
分析: 首先过C作CF∥AB,再证明AB∥FC∥DE,根据平行线的性质可得∠A=∠ACF=40°,∠D=∠FCD,进而得到答案.
解答: 解:过C作CF∥AB,
∵AB∥DE,
∴AB∥FC∥DE,
∴∠A=∠ACF=40°,∠D=∠FCD,
∵∠ACD=100°,
∴∠FCD=100°﹣40°=60°,
∴∠D=60°.
点评: 此题主要考查了平行线的性质,关键是掌握两直线平行,内错角相等.
22.如图,已知直线m∥n,∠1=105°,2=140°,求∠3的大小.
考点: 平行线的性质.
分析: 作直线l∥m∥n,然后根据平行线的性质可得∠1+∠4=180°,∠2+∠5=180°,根据已知求出∠4+∠5的度数,然后根据邻补角的知识求得∠3的度数.
解答: 解:作直线l∥m∥n,
∴∠1+∠4=180°,∠2+∠5=180°,
∵∠1=105°,2=140°,
∴∠4=75°,∠5=40°,
∵∠3为∠4+∠5的邻补角,
∴∠3=180°﹣75°﹣40°=65°.
点评: 本题考查了平行线的性质,关键是作出辅助线,注意掌握平行线的性质:两直线平行,同旁内角互补.
23.已知AB⊥BC,BE∥CF,∠1=∠2,试说明CD⊥BC.
考点: 平行线的性质;垂线.
专题: 证明题.
分析: 先根据垂线的定义得到∠1+∠EBC=90°,再根据平行线的性质得∠EBC=∠FCB,则∠2+∠FCB=∠1+∠EBC=90°,然后根据垂线的定义即可得到结论.
解答: 证明:∵AB⊥BC,
∴∠1+∠EBC=90°,
∵BE∥CF,
∴∠EBC=∠FCB,
∵∠1=∠2,
∴∠2+∠FCB=∠1+∠EBC=90°,
∴CD⊥BC.
点评: 本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.也考查了垂线的定义.
24.如图,已知AB∥CD,∠B=∠D=120°,求∠BOD的度数.
考点: 平行线的性质.
专题: 计算题.
分析: 过O作OE平行于AB,由AB与CD平行,得到OE与CD平行,利用两直线平行同旁内角互补得到两对角互补,由∠B=∠D=120°,求出∠BOE与∠EOD的度数,相加即可确定出∠BOD度数.
解答: 解:过O作OE∥AB,
∵AB∥CD,
∴OE∥CD,
∴∠BOE+∠B=180°,∠EOD+∠D=180°,
∵∠B=∠D=120°,
∴∠BOE=∠EOD=60°,
则∠BOD=∠BOE+∠EOD=120°.
点评: 此题考查了平行线的性质,熟练掌握平行线的性质是解本题的关键.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
