七年级上册5.2平行线综合跟踪训练(含详细解析)
文档属性
| 名称 | 七年级上册5.2平行线综合跟踪训练(含详细解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 290.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-24 15:16:37 | ||
图片预览

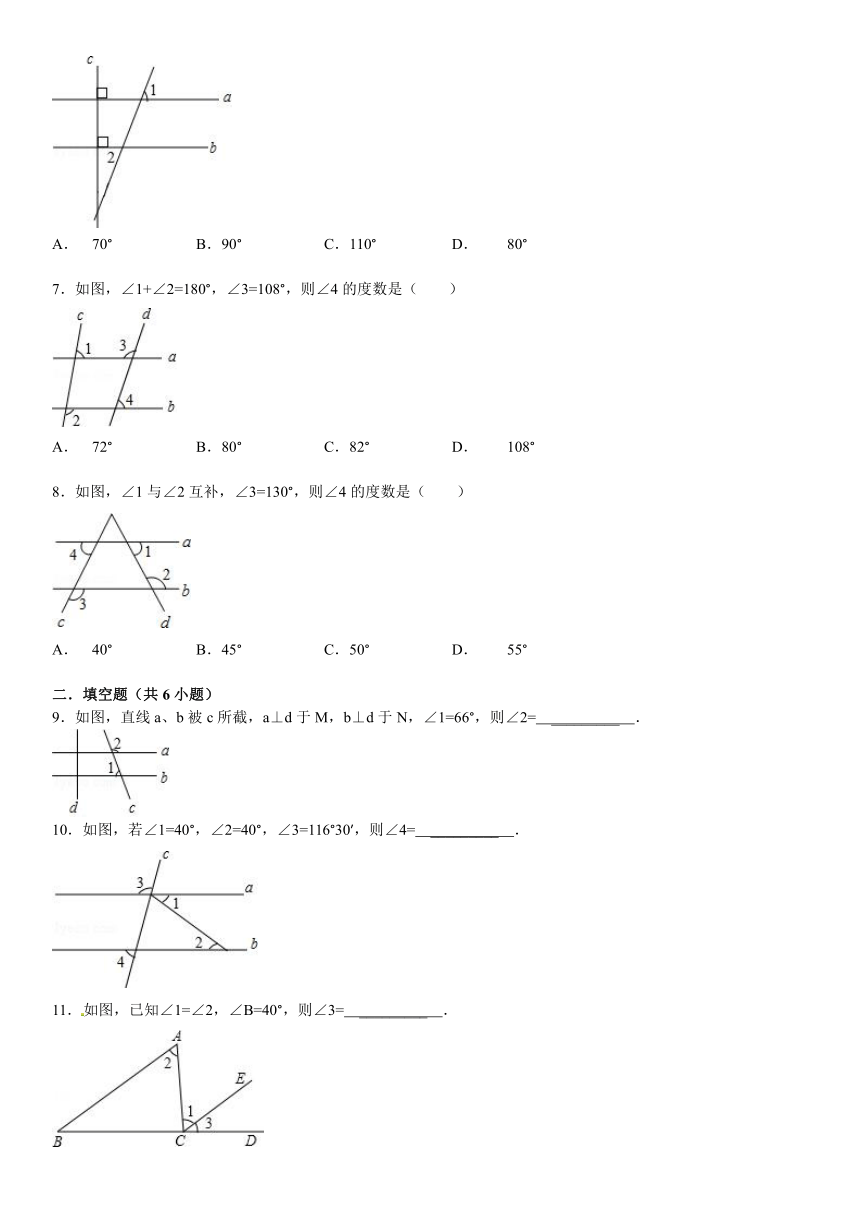
文档简介
第五章相交线与平行线5.2平行线
一.选择题(共8小题)
1.如图,∠1=∠2,∠3=30°,则∠4等于( )
A. 120° B.130° C.145° D. 150°
2.如图,∠1=∠2,∠3=100°,则∠4的度数是( )
A. 70° B.80° C.100° D. 105°
3.下列图形中,由AB∥CD,能得到∠1=∠2的是( )
A. B. C. D.
4.如图,直线a,b,c,d,已知c⊥a,c⊥b,直线b,c,d交于一点,若∠1=50°,则∠2=( )
A. 60° B.50° C.40° D. 30°
5.如图,直线a,b与直线c,d相交,若∠1=∠2,∠3=70°,则∠4的度数是( )
A. 35° B.70° C.90° D. 110°
6.如图,直线a⊥直线c,直线b⊥直线c,若∠1=70°,则∠2=( )
A. 70° B.90° C.110° D. 80°
7.如图,∠1+∠2=180°,∠3=108°,则∠4的度数是( )
A. 72° B.80° C.82° D. 108°
8.如图,∠1与∠2互补,∠3=130°,则∠4的度数是( )
A. 40° B.45° C.50° D. 55°
二.填空题(共6小题)
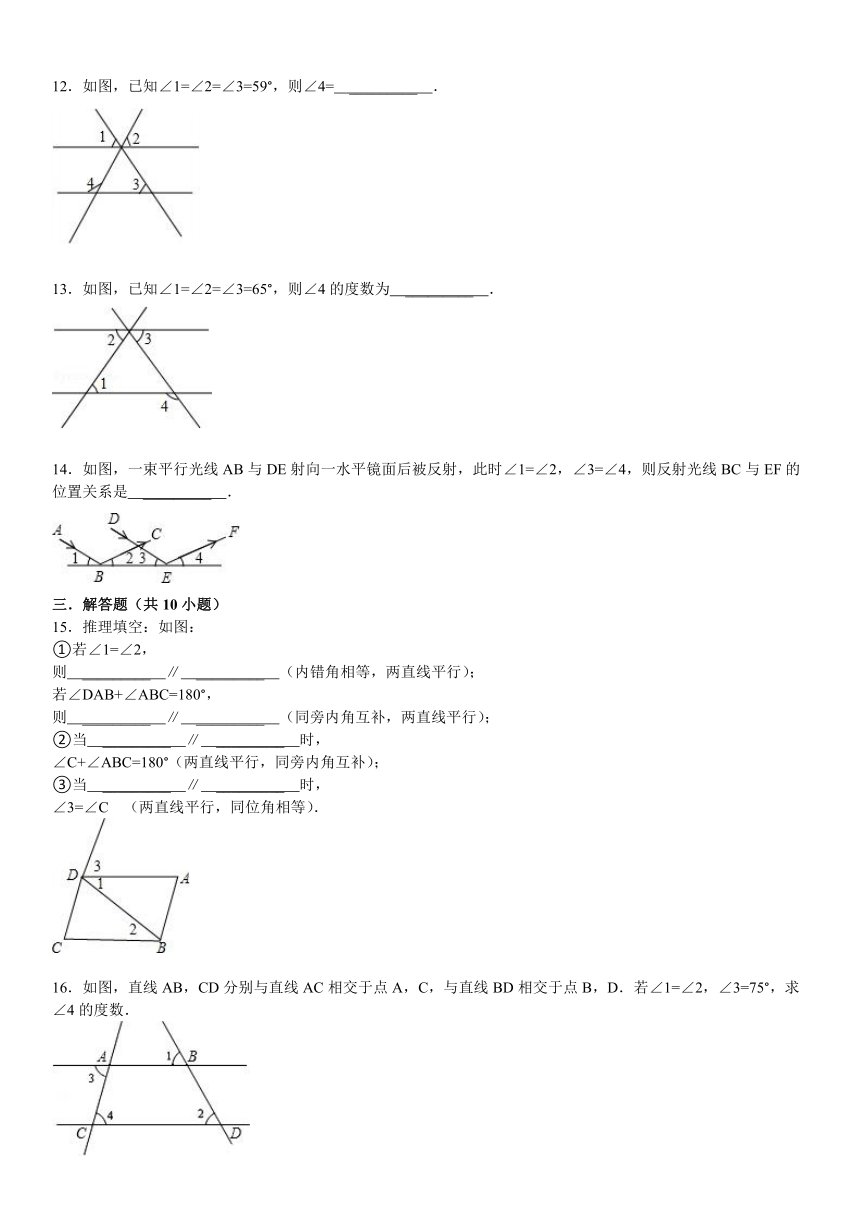
9.如图,直线a、b被c所截,a⊥d于M,b⊥d于N,∠1=66°,则∠2= _________ .
10.如图,若∠1=40°,∠2=40°,∠3=116°30′,则∠4= _________ .
11.如图,已知∠1=∠2,∠B=40°,则∠3= _________ .
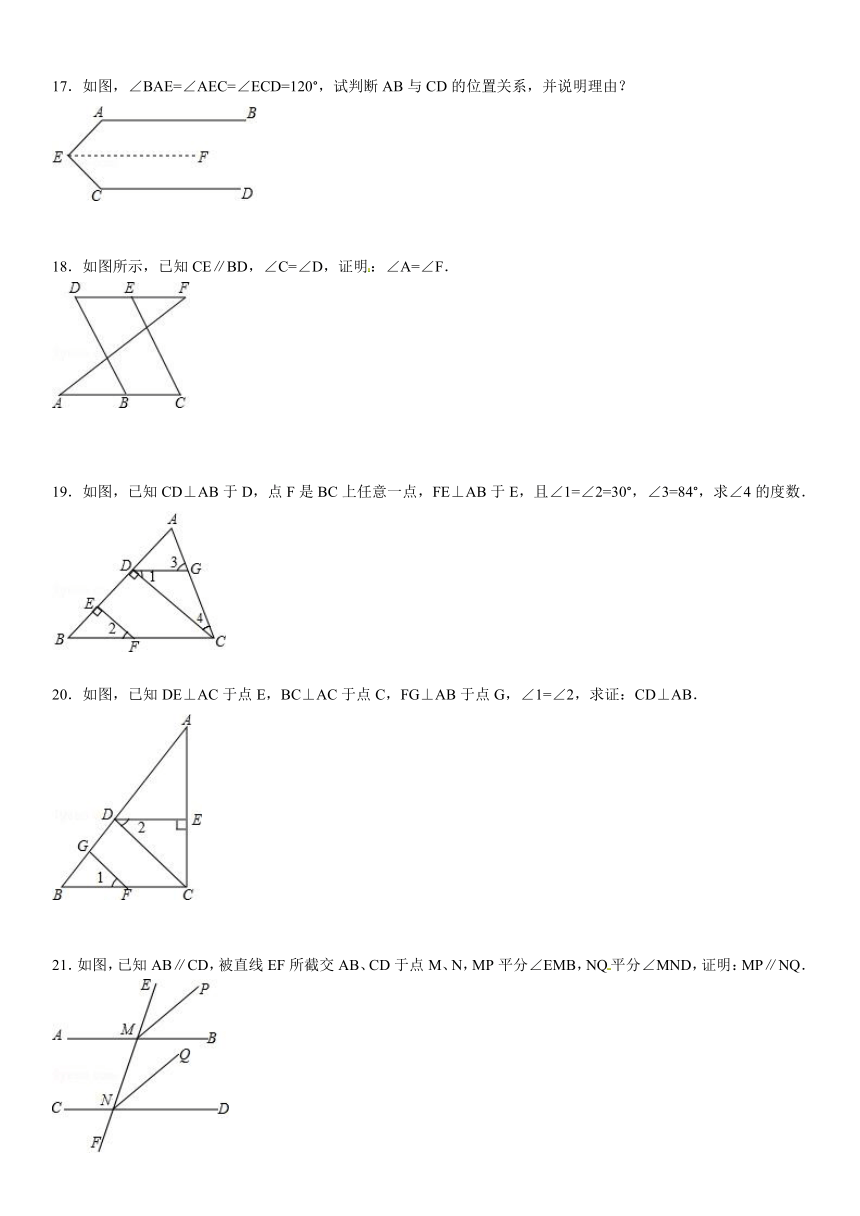
12.如图,已知∠1=∠2=∠3=59°,则∠4= _________ .
13.如图,已知∠1=∠2=∠3=65°,则∠4的度数为 _________ .
14.如图,一束平行光线AB与DE射向一水平镜面后被反射,此时∠1=∠2,∠3=∠4,则反射光线BC与EF的位置关系是 _________ .
三.解答题(共10小题)
15.推理填空:如图:
①若∠1=∠2,
则 _________ ∥ _________ (内错角相等,两直线平行);
若∠DAB+∠ABC=180°,
则 _________ ∥ _________ (同旁内角互补,两直线平行);
②当 _________ ∥ _________ 时,
∠C+∠ABC=180°(两直线平行,同旁内角互补);
③当 _________ ∥ _________ 时,
∠3=∠C (两直线平行,同位角相等).
16.如图,直线AB,CD分别与直线AC相交于点A,C,与直线BD相交于点B,D.若∠1=∠2,∠3=75°,求∠4的度数.
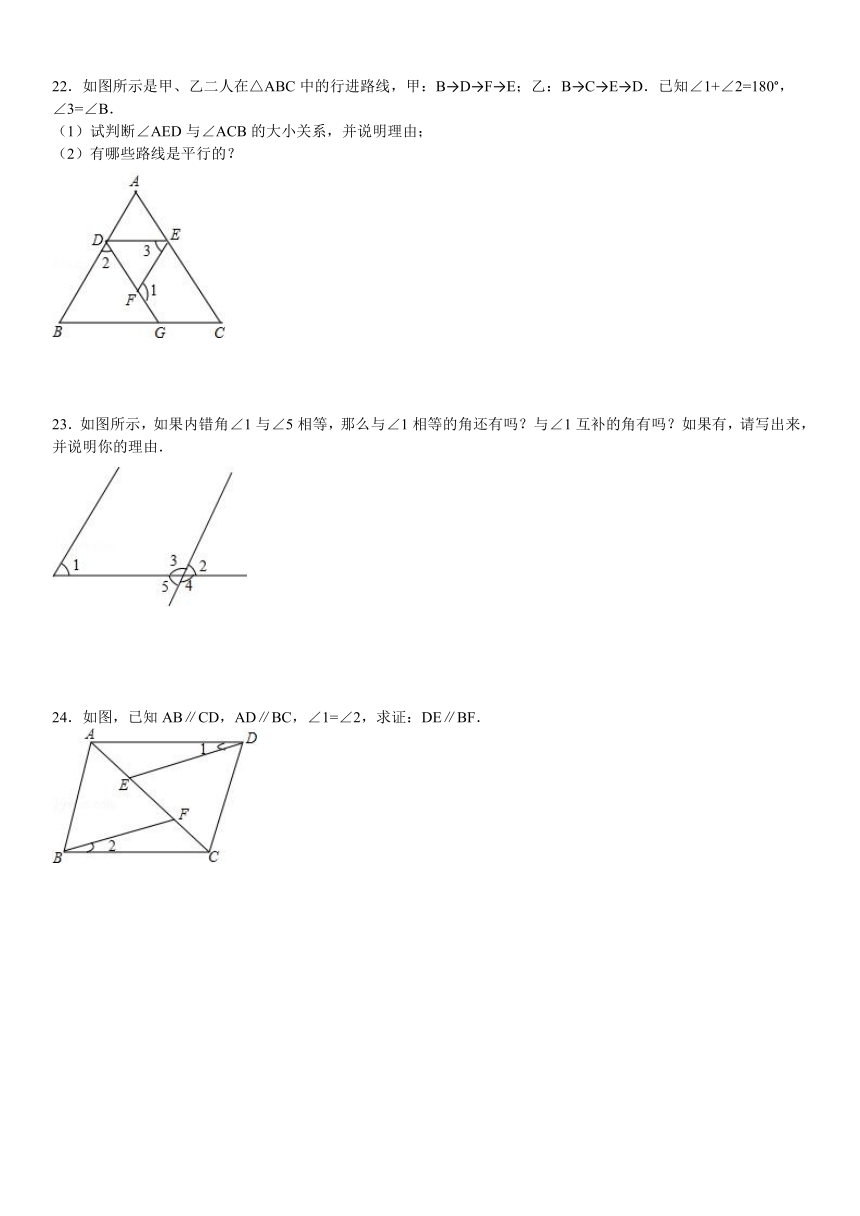
17.如图,∠BAE=∠AEC=∠ECD=120°,试判断AB与CD的位置关系,并说明理由?
18.如图所示,已知CE∥BD,∠C=∠D,证明:∠A=∠F.
19.如图,已知CD⊥AB于D,点F是BC上任意一点,FE⊥AB于E,且∠1=∠2=30°,∠3=84°,求∠4的度数.
20.如图,已知DE⊥AC于点E,BC⊥AC于点C,FG⊥AB于点G,∠1=∠2,求证:CD⊥AB.
21.如图,已知AB∥CD,被直线EF所截交AB、CD于点M、N,MP平分∠EMB,NQ平分∠MND,证明:MP∥NQ.
22.如图所示是甲、乙二人在△ABC中的行进路线,甲:B→D→F→E;乙:B→C→E→D.已知∠1+∠2=180°,∠3=∠B.
(1)试判断∠AED与∠ACB的大小关系,并说明理由;
(2)有哪些路线是平行的?
23.如图所示,如果内错角∠1与∠5相等,那么与∠1相等的角还有吗?与∠1互补的角有吗?如果有,请写出来,并说明你的理由.
24.如图,已知AB∥CD,AD∥BC,∠1=∠2,求证:DE∥BF.
第五章相交线与平行线5.2平行线
参考答案与试题解析
一.选择题(共8小题)
1.如图,∠1=∠2,∠3=30°,则∠4等于( )
A. 120° B.130° C.145° D. 150°
考点: 平行线的判定与性质.
专题: 计算题.
分析: 由∠1=∠2,利用同位角相等两直线平行得到a与b平行,再由两直线平行同位角相等得到∠3=∠5,求出∠5的度数,即可求出∠4的度数.
解答: 解:∵∠1=∠2,
∴a∥b,
∴∠5=∠3=30°,
∴∠4=180°﹣∠5,=150°,
故选D
点评: 此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.
2.如图,∠1=∠2,∠3=100°,则∠4的度数是( )
A. 70° B.80° C.100° D. 105°
考点: 平行线的判定与性质.
专题: 计算题.
分析: 由已知角相等,利用同位角相等两直线平行得到a与b平行,再利用两直线平行同旁内角互补即可求出所求角的度数.
解答: 解:∵∠1=∠2,
∴a∥b,
∴∠3+∠4=180°,
∵∠3=100°,
∴∠4=80°.
故选B
点评: 此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.
3.下列图形中,由AB∥CD,能得到∠1=∠2的是( )
A. B. C. D.
考点: 平行线的判定与性质.
分析: 根据平行线的性质求解即可求得答案,注意掌握排除法在选择题中的应用.
解答: 解:A、∵AB∥CD,
∴∠1+∠2=180°,
故A选项错误;
B、∵AB∥CD,
∴∠1=∠3,
∵∠2=∠3,
∴∠1=∠2,
故B选项正确;
C、∵AB∥CD,
∴∠BAD=∠CDA,
若AC∥BD,可得∠1=∠2;
故C选项错误;
D、若梯形ABCD是等腰梯形,可得∠1=∠2,
故D选项错误.
故选:B.
点评: 此题主要考查了平行线的判定,关键是掌握平行线的判定定理.同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.此题难度不大,注意掌握数形结合思想的应用.
4.如图,直线a,b,c,d,已知c⊥a,c⊥b,直线b,c,d交于一点,若∠1=50°,则∠2=( )
A. 60° B.50° C.40° D. 30°
考点: 平行线的判定与性质.
分析: 先根据对顶角相等得出∠3,然后判断a∥b,再由平行线的性质,可得出∠2的度数.
解答: 解:∵∠1和∠3是对顶角,
∴∠1=∠3=50°,
∵c⊥a,c⊥b,
∴a∥b,
∵∠2=∠3=50°.
故选:B.
点评: 本题考查了平行线的判定与性质,解答本题的关键是掌握两直线平行内错角相等,对顶角相等.
5.如图,直线a,b与直线c,d相交,若∠1=∠2,∠3=70°,则∠4的度数是( )
A. 35° B.70° C.90° D. 110°
考点: 平行线的判定与性质.
分析: 首先根据∠1=∠2,可根据同位角相等,两直线平行判断出a∥b,可得∠3=∠5,再根据邻补角互补可以计算出∠4的度数.
解答: 解:∵∠1=∠2,
∴a∥b,
∴∠3=∠5,
∵∠3=70°,
∴∠5=70°,
∴∠4=180°﹣70°=110°,
故选:D.
点评: 此题主要考查了平行线的判定与性质,关键是掌握平行线的判定定理与性质定理,平行线的判定是由角的数量关系判断两直线的位置关系.平行线的性质是由平行关系来寻找角的数量关系
6.如图,直线a⊥直线c,直线b⊥直线c,若∠1=70°,则∠2=( )
A. 70° B.90° C.110° D. 80°
考点: 平行线的判定与性质;对顶角、邻补角;直角三角形的性质.
分析: 首先根据垂直于同一条直线的两直线平行可得a∥b,再根据两直线平行同位角相等可得∠1=∠3.根据对顶角相等可得∠2=∠3,利用等量代换可得到∠2=∠1=70°.
解答: 解:∵直线a⊥直线c,直线b⊥直线c,
∴a∥b,
∴∠1=∠3,
∵∠3=∠2,
∴∠2=∠1=70°.
故选:A.
点评: 此题主要考查了平行线的判定与性质,关键是掌握平行线的判定方法与性质定理.
7.如图,∠1+∠2=180°,∠3=108°,则∠4的度数是( )
A. 72° B.80° C.82° D. 108°
考点: 平行线的判定与性质.
专题: 计算题.
分析: 由邻补角定义得到∠2与∠5互补,再由∠1与∠2互补,利用同角的补角相等得到∠1=∠5,利用同位角相等两直线平行得到a与b平行,利用两直线平行同旁内角互补得到∠6与∠4互补,而∠3与∠6对顶角相等,由∠3的度数求出∠6的度数,进而求出∠4的度数.
解答: 解:∵∠1+∠2=180°,∠2+∠5=180°,
∴∠1=∠5,
∴a∥b,
∴∠4+∠6=180°,
∴∠4=72°.
故选:A.
点评: 此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.
8.如图,∠1与∠2互补,∠3=130°,则∠4的度数是( )
A. 40° B.45° C.50° D. 55°
考点: 平行线的判定与性质.
分析: 由平行线的判定定理证得a∥b;然后根据平行线的性质、对顶角相等即可求得∠4的度数.
解答: 解:∵∠1与∠2互补,
∴a∥b(同旁内角互补,两直线平行),
∴∠4+∠5=180°(两直线平行,同旁内角互补);
又∵∠3=∠5(对顶角相等),∠3=130°(已知),
∴∠4=50°.
故选C.
点评: 本题考查了平行线的判定与性质.解答此题的关键是注意平行线的性质(两直线平行,同旁内角互补)和判定定理(同旁内角互补,两直线平行)的综合运用.
二.填空题(共6小题)
9.如图,直线a、b被c所截,a⊥d于M,b⊥d于N,∠1=66°,则∠2= 114° .
考点: 平行线的判定与性质.
分析: 根据a⊥d,b⊥d,可得出a∥b,再根据两直线平行,内错角相等,求得∠2即可.
解答: 解:∵a⊥d,b⊥d,
∴a∥b,
∴∠1=∠2,
∵∠1=66°,
∴∠2=114°,
故答案为114°.
点评: 本题考查了平行线的判定和性质,根据两条直线同垂直于一条直线,这两条直线平行.
10.如图,若∠1=40°,∠2=40°,∠3=116°30′,则∠4= 63°30′ .
考点: 平行线的判定与性质.
分析: 根据∠1=∠2可以判定a∥b,再根据平行线的性质可得∠3=∠5,再根据邻补角互补可得答案.
解答: 解:∵∠1=40°,∠2=40°,
∴a∥b,
∴∠3=∠5=116°30′,
∴∠4=180°﹣116°30′=63°30′,
故答案为:63°30′.
点评: 此题主要考查了平行线的判定与性质,关键是掌握同位角相等,两直线平行.
11.如图,已知∠1=∠2,∠B=40°,则∠3= 40° .
考点: 平行线的判定与性质.
专题: 计算题.
分析: 由∠1=∠2,根据“内错角相等,两直线平行”得AB∥CE,再根据两直线平行,同位角相等即可得到∠3=∠B=40°.
解答: 解:∵∠1=∠2,
∴AB∥CE,
∴∠3=∠B,
而∠B=40°,
∴∠3=40°.
故答案为40°.
点评: 本题考查了平行线的判定与性质:内错角相等,两直线平行;两直线平行,同位角相等.
12.如图,已知∠1=∠2=∠3=59°,则∠4= 121° .
考点: 平行线的判定与性质.
专题: 计算题.
分析: 由∠1=∠3,利用同位角相等两直线平行,得到AB与CD平行,再利用两直线平行同旁内角互补得到∠5与∠4互补,利用对顶角相等得到∠5=∠2,由∠2的度数求出∠5的度数,即可求出∠4的度数.
解答:
解:∵∠1=∠3,
∴AB∥CD,
∴∠5+∠4=180°,又∠5=∠2=59°,
∴∠4=180°﹣59°=121°.
故答案为:121°
点评: 此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.
13.如图,已知∠1=∠2=∠3=65°,则∠4的度数为 115° .
考点: 平行线的判定与性质.
专题: 计算题.
分析: 根据平行线的判定与性质,可得∠3=∠5=65°,又根据邻补角可得∠5+∠4=180°,即可得出∠4的度数;
解答: 解:∵∠1=∠2,
∴AB∥CD,
∴∠3=∠5,又∠1=∠2=∠3=65°,
∴∠5=65°又∠5+∠4=180°,
∴∠4=115°;
故答案为:115°.
点评: 本题主要考查了平行线的判定与性质,解答此题的关键是注意平行线的性质和判定定理的综合运用.
14.如图,一束平行光线AB与DE射向一水平镜面后被反射,此时∠1=∠2,∠3=∠4,则反射光线BC与EF的位置关系是 平行 .
考点: 平行线的判定与性质.
专题: 跨学科.
分析: 根据平行线的性质和判定解答.
解答: 解:∵AB∥DE,
∴∠1=∠3 (两直线平行,同位角相等),
又∵∠1=∠2,∠3=∠4,
∴∠2=∠4,
∴BC∥EF(同位角相等,两直线平行),
故填平行.
点评: 此题考查平行线的性质和判定,综合了光学的有关知识.
三.解答题(共10小题)
15.推理填空:如图:
①若∠1=∠2,
则 AD ∥ CB (内错角相等,两直线平行);
若∠DAB+∠ABC=180°,
则 AD ∥ BC (同旁内角互补,两直线平行);
②当 AB ∥ CD 时,
∠C+∠ABC=180°(两直线平行,同旁内角互补);
③当 AD ∥ BC 时,
∠3=∠C (两直线平行,同位角相等).
考点: 平行线的判定与性质.
专题: 推理填空题.
分析: 根据平行线的性质和平行线的判定直接完成填空.两条直线平行,则同位角相等,内错角相等,同旁内角互补;反之亦成立.
解答: 解:①若∠1=∠2,
则AD∥CB(内错角相等,两条直线平行);
若∠DAB+∠ABC=180°,
则AD∥BC(同旁内角互补,两条直线平行);
②当AB∥CD时,
∠C+∠ABC=180°(两条直线平行,同旁内角互补);
③当AD∥BC时,
∠3=∠C (两条直线平行,同位角相等).
点评: 在做此类题的时候,一定要细心观察,看两个角到底是哪两条直线被第三条直线所截而形成的角.
16.如图,直线AB,CD分别与直线AC相交于点A,C,与直线BD相交于点B,D.若∠1=∠2,∠3=75°,求∠4的度数.
考点: 平行线的判定与性质.
分析: 根据平行线的判定得出AB∥CD,从而得出∠3=∠4,即可得出答案.
解答: 解:∵∠1=∠2,
∴AB∥CD(同位角相等,两直线平行),
∴∠4=∠3=75°(两直线平行,内错角相等).
点评: 本题主要考查了平行线的判定与性质,比较简单.
17.如图,∠BAE=∠AEC=∠ECD=120°,试判断AB与CD的位置关系,并说明理由?
考点: 平行线的判定与性质.
分析: 如图,过点E做EF∥AB.根据“两直线平行,同旁内角互补”求得∠1=60°.则易求∠2=60°,故∠2+∠ECD=180°.根据“同旁内角互补,两直线平行”推知EF∥CD,则AB∥CD.
解答: 解:AB∥CD.理由如下:
如图,过点E做EF∥AB.则∠EAB∠1=180°.
∵∠BAE=120°,
∴∠1=60°.
又∵∠AEC=120°,
∴∠2=60°,
∴∠2+∠ECD=180°,
∴EF∥CD,
∴AB∥CD.
点评: 本题考查了平行线的判定与性质.注意辅助线的作法.
18.如图所示,已知CE∥BD,∠C=∠D,证明:∠A=∠F.
考点: 平行线的判定与性质.
专题: 证明题.
分析: 先根据平行线的性质得出∠C=∠DBA,再由∠C=∠D等量代换得到∠DBA=∠D,根据内错角相等,两直线平行得出DF∥AC,然后由两直线平行,内错角相等,即可证明∠A=∠F.
解答: 证明:∵CE∥BD,
∴∠C=∠DBA,
∵∠C=∠D,
∴∠DBA=∠D,
∴DF∥AC,
∴∠A=∠F.
点评: 本题考查了平行线的判定与性质,熟记定理与性质是解题的关键.
19.如图,已知CD⊥AB于D,点F是BC上任意一点,FE⊥AB于E,且∠1=∠2=30°,∠3=84°,求∠4的度数.
考点: 平行线的判定与性质;三角形的外角性质.
专题: 计算题.
分析: 根据垂直的定义得∠BEF=∠BDC=90°,根据平行线的判定得FE∥CD,则根据平行线的性质得∠2=∠BCD,由于∠1=∠2=30°,则∠1=∠BCD=30°,可判断DG∥BC,利用平行线的性质得∠3=∠ACB=∠4+∠BCD,所以∠4=54°.
解答: 解:∵CD⊥AB,FE⊥AB,
∴∠BEF=∠BDC=90°,
∴FE∥CD,
∴∠2=∠BCD,
∵∠1=∠2=30°,
∴∠1=∠BCD=30°,
∴DG∥BC,
∴∠3=∠ACB=∠4+∠BCD,
∴∠4=84°﹣30°=54°.
点评: 本题考查了平行线的判定与性质:同位角相等,两直线平行;内错角相等,两直线平行;两直线平行,同位角相等.
20.如图,已知DE⊥AC于点E,BC⊥AC于点C,FG⊥AB于点G,∠1=∠2,求证:CD⊥AB.
考点: 平行线的判定与性质.
专题: 证明题.
分析: 根据垂直于同一直线的两直线互相平行可得DE∥BC,再根据两直线平行,内错角相等可得∠2=∠3,然后求出∠1=∠3,根据同位角相等两直线平行可得GF∥CD,再根据垂直于同一直线的两直线互相平行证明.
解答: 证明:∵DE⊥AC,BC⊥AC,
∴DE∥BC,
∴∠2=∠3,
∵∠1=∠2,
∴∠1=∠3,
∴GF∥CD,
∵FG⊥AB,
∴CD⊥AB.
点评: 本题考查了平行线的判定与性质,垂直于同一直线的两直线平行,熟记性质是解题的关键.
21.如图,已知AB∥CD,被直线EF所截交AB、CD于点M、N,MP平分∠EMB,NQ平分∠MND,证明:MP∥NQ.
考点: 平行线的判定与性质.
专题: 证明题.
分析: 由AB∥CD,根据平行线的性质得∠EMB=∠MND,再根据角平分线的定义得到∠EMP=∠EMB,∠MNQ=∠MND,则∠EMP=∠MNQ,然后根据平行线的判定即可得到MP∥NQ.
解答: 证明:∵AB∥CD,
∴∠EMB=∠MND,
∵N,MP平分∠EMB,NQ平分∠MND,
∴∠EMP=∠EMB,∠MNQ=∠MND,
∴∠EMP=∠MNQ,
∴MP∥NQ.
点评: 本题考查了平行线的判定与性质:两直线平行,同位角相等;同位角相等,两直线平行.
22.如图所示是甲、乙二人在△ABC中的行进路线,甲:B→D→F→E;乙:B→C→E→D.已知∠1+∠2=180°,∠3=∠B.
(1)试判断∠AED与∠ACB的大小关系,并说明理由;
(2)有哪些路线是平行的?
考点: 平行线的判定与性质.
分析: (1)根据“同旁内角互补,两直线平行”推知EF∥AB,则“两直线平行,内错角相等”:∠3=∠5,所以结合已知条件推知∠5=∠B,故DE∥BC,所以∠AED=∠ACB;
(2)由(1)的推理过程来写出图中的平行线.
解答: 解:(1)∠AED=∠ACB.理由如下:
如图,∵∠1+∠2=180°,∠1+∠4=180°,
∴∠2=∠4,
∴EF∥AB,
∴∠3=∠5.
又∵∠3=∠B,
∴DE∥BC,
∴∠AED=∠ACB;
(2)由(1)知,BD与FE平行,BC与ED平行.
点评: 本题考查了平行线的判定与性质.解答此题的关键是注意平行线的性质和判定定理的综合运用.
23.如图所示,如果内错角∠1与∠5相等,那么与∠1相等的角还有吗?与∠1互补的角有吗?如果有,请写出来,并说明你的理由.
考点: 平行线的判定与性质;余角和补角.
分析: 根据平行线的判定定理推知a∥b,则利用平行线的性质和对顶角相等以及等量代换进行解答.
解答: 解:∠1=∠2=∠5,1+∠3=∠1+∠4=180°.
理由如下:
∵内错角∠1与∠5相等,
∴a∥b,
∴∠1=∠2(两直线平行,同位角相等),∠1+∠3=180°(两直线平行,同旁内角互补),
又∵∠2=∠5、∠3=∠4(对顶角相等),
∴∠1=∠2=∠5,1+∠3=∠1+∠4=180°(等量代换).
点评: 本题考查了平行线的判定与性质、余角和补角.利用已知条件判定a∥b是解题的关键.
24.如图,已知AB∥CD,AD∥BC,∠1=∠2,求证:DE∥BF.
考点: 平行线的判定与性质.
专题: 证明题.
分析: 由AB与CD平行,AD与BC平行,得到四边形ABCD为平行四边形,且得到一对内错角相等,根据平行四边形的对边相等得到AD=CB,利用ASA得到三角形ADE与三角形BCF全等,利用全等三角形的对应角相等得到一对角相等,再利用等角的补角相等得到一对内错角相等,利用内错角相等两直线平行即可得证.
解答: 证明:∵AB∥CD,AD∥BC,
∴四边形ABCD为平行四边形,且∠DAE=∠BCF,
∴AD=BC,
在△ADE和△BCF中,
,
∴△ADE≌△BCF(ASA),
∴∠AED=∠CFB,
∵∠AED+∠DEC=180°,∠CFB+∠AFB=180°,
∴∠DEC=∠AFB,
∴DE∥BF.
点评: 此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.
一.选择题(共8小题)
1.如图,∠1=∠2,∠3=30°,则∠4等于( )
A. 120° B.130° C.145° D. 150°
2.如图,∠1=∠2,∠3=100°,则∠4的度数是( )
A. 70° B.80° C.100° D. 105°
3.下列图形中,由AB∥CD,能得到∠1=∠2的是( )
A. B. C. D.
4.如图,直线a,b,c,d,已知c⊥a,c⊥b,直线b,c,d交于一点,若∠1=50°,则∠2=( )
A. 60° B.50° C.40° D. 30°
5.如图,直线a,b与直线c,d相交,若∠1=∠2,∠3=70°,则∠4的度数是( )
A. 35° B.70° C.90° D. 110°
6.如图,直线a⊥直线c,直线b⊥直线c,若∠1=70°,则∠2=( )
A. 70° B.90° C.110° D. 80°
7.如图,∠1+∠2=180°,∠3=108°,则∠4的度数是( )
A. 72° B.80° C.82° D. 108°
8.如图,∠1与∠2互补,∠3=130°,则∠4的度数是( )
A. 40° B.45° C.50° D. 55°
二.填空题(共6小题)
9.如图,直线a、b被c所截,a⊥d于M,b⊥d于N,∠1=66°,则∠2= _________ .
10.如图,若∠1=40°,∠2=40°,∠3=116°30′,则∠4= _________ .
11.如图,已知∠1=∠2,∠B=40°,则∠3= _________ .
12.如图,已知∠1=∠2=∠3=59°,则∠4= _________ .
13.如图,已知∠1=∠2=∠3=65°,则∠4的度数为 _________ .
14.如图,一束平行光线AB与DE射向一水平镜面后被反射,此时∠1=∠2,∠3=∠4,则反射光线BC与EF的位置关系是 _________ .
三.解答题(共10小题)
15.推理填空:如图:
①若∠1=∠2,
则 _________ ∥ _________ (内错角相等,两直线平行);
若∠DAB+∠ABC=180°,
则 _________ ∥ _________ (同旁内角互补,两直线平行);
②当 _________ ∥ _________ 时,
∠C+∠ABC=180°(两直线平行,同旁内角互补);
③当 _________ ∥ _________ 时,
∠3=∠C (两直线平行,同位角相等).
16.如图,直线AB,CD分别与直线AC相交于点A,C,与直线BD相交于点B,D.若∠1=∠2,∠3=75°,求∠4的度数.
17.如图,∠BAE=∠AEC=∠ECD=120°,试判断AB与CD的位置关系,并说明理由?
18.如图所示,已知CE∥BD,∠C=∠D,证明:∠A=∠F.
19.如图,已知CD⊥AB于D,点F是BC上任意一点,FE⊥AB于E,且∠1=∠2=30°,∠3=84°,求∠4的度数.
20.如图,已知DE⊥AC于点E,BC⊥AC于点C,FG⊥AB于点G,∠1=∠2,求证:CD⊥AB.
21.如图,已知AB∥CD,被直线EF所截交AB、CD于点M、N,MP平分∠EMB,NQ平分∠MND,证明:MP∥NQ.
22.如图所示是甲、乙二人在△ABC中的行进路线,甲:B→D→F→E;乙:B→C→E→D.已知∠1+∠2=180°,∠3=∠B.
(1)试判断∠AED与∠ACB的大小关系,并说明理由;
(2)有哪些路线是平行的?
23.如图所示,如果内错角∠1与∠5相等,那么与∠1相等的角还有吗?与∠1互补的角有吗?如果有,请写出来,并说明你的理由.
24.如图,已知AB∥CD,AD∥BC,∠1=∠2,求证:DE∥BF.
第五章相交线与平行线5.2平行线
参考答案与试题解析
一.选择题(共8小题)
1.如图,∠1=∠2,∠3=30°,则∠4等于( )
A. 120° B.130° C.145° D. 150°
考点: 平行线的判定与性质.
专题: 计算题.
分析: 由∠1=∠2,利用同位角相等两直线平行得到a与b平行,再由两直线平行同位角相等得到∠3=∠5,求出∠5的度数,即可求出∠4的度数.
解答: 解:∵∠1=∠2,
∴a∥b,
∴∠5=∠3=30°,
∴∠4=180°﹣∠5,=150°,
故选D
点评: 此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.
2.如图,∠1=∠2,∠3=100°,则∠4的度数是( )
A. 70° B.80° C.100° D. 105°
考点: 平行线的判定与性质.
专题: 计算题.
分析: 由已知角相等,利用同位角相等两直线平行得到a与b平行,再利用两直线平行同旁内角互补即可求出所求角的度数.
解答: 解:∵∠1=∠2,
∴a∥b,
∴∠3+∠4=180°,
∵∠3=100°,
∴∠4=80°.
故选B
点评: 此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.
3.下列图形中,由AB∥CD,能得到∠1=∠2的是( )
A. B. C. D.
考点: 平行线的判定与性质.
分析: 根据平行线的性质求解即可求得答案,注意掌握排除法在选择题中的应用.
解答: 解:A、∵AB∥CD,
∴∠1+∠2=180°,
故A选项错误;
B、∵AB∥CD,
∴∠1=∠3,
∵∠2=∠3,
∴∠1=∠2,
故B选项正确;
C、∵AB∥CD,
∴∠BAD=∠CDA,
若AC∥BD,可得∠1=∠2;
故C选项错误;
D、若梯形ABCD是等腰梯形,可得∠1=∠2,
故D选项错误.
故选:B.
点评: 此题主要考查了平行线的判定,关键是掌握平行线的判定定理.同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.此题难度不大,注意掌握数形结合思想的应用.
4.如图,直线a,b,c,d,已知c⊥a,c⊥b,直线b,c,d交于一点,若∠1=50°,则∠2=( )
A. 60° B.50° C.40° D. 30°
考点: 平行线的判定与性质.
分析: 先根据对顶角相等得出∠3,然后判断a∥b,再由平行线的性质,可得出∠2的度数.
解答: 解:∵∠1和∠3是对顶角,
∴∠1=∠3=50°,
∵c⊥a,c⊥b,
∴a∥b,
∵∠2=∠3=50°.
故选:B.
点评: 本题考查了平行线的判定与性质,解答本题的关键是掌握两直线平行内错角相等,对顶角相等.
5.如图,直线a,b与直线c,d相交,若∠1=∠2,∠3=70°,则∠4的度数是( )
A. 35° B.70° C.90° D. 110°
考点: 平行线的判定与性质.
分析: 首先根据∠1=∠2,可根据同位角相等,两直线平行判断出a∥b,可得∠3=∠5,再根据邻补角互补可以计算出∠4的度数.
解答: 解:∵∠1=∠2,
∴a∥b,
∴∠3=∠5,
∵∠3=70°,
∴∠5=70°,
∴∠4=180°﹣70°=110°,
故选:D.
点评: 此题主要考查了平行线的判定与性质,关键是掌握平行线的判定定理与性质定理,平行线的判定是由角的数量关系判断两直线的位置关系.平行线的性质是由平行关系来寻找角的数量关系
6.如图,直线a⊥直线c,直线b⊥直线c,若∠1=70°,则∠2=( )
A. 70° B.90° C.110° D. 80°
考点: 平行线的判定与性质;对顶角、邻补角;直角三角形的性质.
分析: 首先根据垂直于同一条直线的两直线平行可得a∥b,再根据两直线平行同位角相等可得∠1=∠3.根据对顶角相等可得∠2=∠3,利用等量代换可得到∠2=∠1=70°.
解答: 解:∵直线a⊥直线c,直线b⊥直线c,
∴a∥b,
∴∠1=∠3,
∵∠3=∠2,
∴∠2=∠1=70°.
故选:A.
点评: 此题主要考查了平行线的判定与性质,关键是掌握平行线的判定方法与性质定理.
7.如图,∠1+∠2=180°,∠3=108°,则∠4的度数是( )
A. 72° B.80° C.82° D. 108°
考点: 平行线的判定与性质.
专题: 计算题.
分析: 由邻补角定义得到∠2与∠5互补,再由∠1与∠2互补,利用同角的补角相等得到∠1=∠5,利用同位角相等两直线平行得到a与b平行,利用两直线平行同旁内角互补得到∠6与∠4互补,而∠3与∠6对顶角相等,由∠3的度数求出∠6的度数,进而求出∠4的度数.
解答: 解:∵∠1+∠2=180°,∠2+∠5=180°,
∴∠1=∠5,
∴a∥b,
∴∠4+∠6=180°,
∴∠4=72°.
故选:A.
点评: 此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.
8.如图,∠1与∠2互补,∠3=130°,则∠4的度数是( )
A. 40° B.45° C.50° D. 55°
考点: 平行线的判定与性质.
分析: 由平行线的判定定理证得a∥b;然后根据平行线的性质、对顶角相等即可求得∠4的度数.
解答: 解:∵∠1与∠2互补,
∴a∥b(同旁内角互补,两直线平行),
∴∠4+∠5=180°(两直线平行,同旁内角互补);
又∵∠3=∠5(对顶角相等),∠3=130°(已知),
∴∠4=50°.
故选C.
点评: 本题考查了平行线的判定与性质.解答此题的关键是注意平行线的性质(两直线平行,同旁内角互补)和判定定理(同旁内角互补,两直线平行)的综合运用.
二.填空题(共6小题)
9.如图,直线a、b被c所截,a⊥d于M,b⊥d于N,∠1=66°,则∠2= 114° .
考点: 平行线的判定与性质.
分析: 根据a⊥d,b⊥d,可得出a∥b,再根据两直线平行,内错角相等,求得∠2即可.
解答: 解:∵a⊥d,b⊥d,
∴a∥b,
∴∠1=∠2,
∵∠1=66°,
∴∠2=114°,
故答案为114°.
点评: 本题考查了平行线的判定和性质,根据两条直线同垂直于一条直线,这两条直线平行.
10.如图,若∠1=40°,∠2=40°,∠3=116°30′,则∠4= 63°30′ .
考点: 平行线的判定与性质.
分析: 根据∠1=∠2可以判定a∥b,再根据平行线的性质可得∠3=∠5,再根据邻补角互补可得答案.
解答: 解:∵∠1=40°,∠2=40°,
∴a∥b,
∴∠3=∠5=116°30′,
∴∠4=180°﹣116°30′=63°30′,
故答案为:63°30′.
点评: 此题主要考查了平行线的判定与性质,关键是掌握同位角相等,两直线平行.
11.如图,已知∠1=∠2,∠B=40°,则∠3= 40° .
考点: 平行线的判定与性质.
专题: 计算题.
分析: 由∠1=∠2,根据“内错角相等,两直线平行”得AB∥CE,再根据两直线平行,同位角相等即可得到∠3=∠B=40°.
解答: 解:∵∠1=∠2,
∴AB∥CE,
∴∠3=∠B,
而∠B=40°,
∴∠3=40°.
故答案为40°.
点评: 本题考查了平行线的判定与性质:内错角相等,两直线平行;两直线平行,同位角相等.
12.如图,已知∠1=∠2=∠3=59°,则∠4= 121° .
考点: 平行线的判定与性质.
专题: 计算题.
分析: 由∠1=∠3,利用同位角相等两直线平行,得到AB与CD平行,再利用两直线平行同旁内角互补得到∠5与∠4互补,利用对顶角相等得到∠5=∠2,由∠2的度数求出∠5的度数,即可求出∠4的度数.
解答:
解:∵∠1=∠3,
∴AB∥CD,
∴∠5+∠4=180°,又∠5=∠2=59°,
∴∠4=180°﹣59°=121°.
故答案为:121°
点评: 此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.
13.如图,已知∠1=∠2=∠3=65°,则∠4的度数为 115° .
考点: 平行线的判定与性质.
专题: 计算题.
分析: 根据平行线的判定与性质,可得∠3=∠5=65°,又根据邻补角可得∠5+∠4=180°,即可得出∠4的度数;
解答: 解:∵∠1=∠2,
∴AB∥CD,
∴∠3=∠5,又∠1=∠2=∠3=65°,
∴∠5=65°又∠5+∠4=180°,
∴∠4=115°;
故答案为:115°.
点评: 本题主要考查了平行线的判定与性质,解答此题的关键是注意平行线的性质和判定定理的综合运用.
14.如图,一束平行光线AB与DE射向一水平镜面后被反射,此时∠1=∠2,∠3=∠4,则反射光线BC与EF的位置关系是 平行 .
考点: 平行线的判定与性质.
专题: 跨学科.
分析: 根据平行线的性质和判定解答.
解答: 解:∵AB∥DE,
∴∠1=∠3 (两直线平行,同位角相等),
又∵∠1=∠2,∠3=∠4,
∴∠2=∠4,
∴BC∥EF(同位角相等,两直线平行),
故填平行.
点评: 此题考查平行线的性质和判定,综合了光学的有关知识.
三.解答题(共10小题)
15.推理填空:如图:
①若∠1=∠2,
则 AD ∥ CB (内错角相等,两直线平行);
若∠DAB+∠ABC=180°,
则 AD ∥ BC (同旁内角互补,两直线平行);
②当 AB ∥ CD 时,
∠C+∠ABC=180°(两直线平行,同旁内角互补);
③当 AD ∥ BC 时,
∠3=∠C (两直线平行,同位角相等).
考点: 平行线的判定与性质.
专题: 推理填空题.
分析: 根据平行线的性质和平行线的判定直接完成填空.两条直线平行,则同位角相等,内错角相等,同旁内角互补;反之亦成立.
解答: 解:①若∠1=∠2,
则AD∥CB(内错角相等,两条直线平行);
若∠DAB+∠ABC=180°,
则AD∥BC(同旁内角互补,两条直线平行);
②当AB∥CD时,
∠C+∠ABC=180°(两条直线平行,同旁内角互补);
③当AD∥BC时,
∠3=∠C (两条直线平行,同位角相等).
点评: 在做此类题的时候,一定要细心观察,看两个角到底是哪两条直线被第三条直线所截而形成的角.
16.如图,直线AB,CD分别与直线AC相交于点A,C,与直线BD相交于点B,D.若∠1=∠2,∠3=75°,求∠4的度数.
考点: 平行线的判定与性质.
分析: 根据平行线的判定得出AB∥CD,从而得出∠3=∠4,即可得出答案.
解答: 解:∵∠1=∠2,
∴AB∥CD(同位角相等,两直线平行),
∴∠4=∠3=75°(两直线平行,内错角相等).
点评: 本题主要考查了平行线的判定与性质,比较简单.
17.如图,∠BAE=∠AEC=∠ECD=120°,试判断AB与CD的位置关系,并说明理由?
考点: 平行线的判定与性质.
分析: 如图,过点E做EF∥AB.根据“两直线平行,同旁内角互补”求得∠1=60°.则易求∠2=60°,故∠2+∠ECD=180°.根据“同旁内角互补,两直线平行”推知EF∥CD,则AB∥CD.
解答: 解:AB∥CD.理由如下:
如图,过点E做EF∥AB.则∠EAB∠1=180°.
∵∠BAE=120°,
∴∠1=60°.
又∵∠AEC=120°,
∴∠2=60°,
∴∠2+∠ECD=180°,
∴EF∥CD,
∴AB∥CD.
点评: 本题考查了平行线的判定与性质.注意辅助线的作法.
18.如图所示,已知CE∥BD,∠C=∠D,证明:∠A=∠F.
考点: 平行线的判定与性质.
专题: 证明题.
分析: 先根据平行线的性质得出∠C=∠DBA,再由∠C=∠D等量代换得到∠DBA=∠D,根据内错角相等,两直线平行得出DF∥AC,然后由两直线平行,内错角相等,即可证明∠A=∠F.
解答: 证明:∵CE∥BD,
∴∠C=∠DBA,
∵∠C=∠D,
∴∠DBA=∠D,
∴DF∥AC,
∴∠A=∠F.
点评: 本题考查了平行线的判定与性质,熟记定理与性质是解题的关键.
19.如图,已知CD⊥AB于D,点F是BC上任意一点,FE⊥AB于E,且∠1=∠2=30°,∠3=84°,求∠4的度数.
考点: 平行线的判定与性质;三角形的外角性质.
专题: 计算题.
分析: 根据垂直的定义得∠BEF=∠BDC=90°,根据平行线的判定得FE∥CD,则根据平行线的性质得∠2=∠BCD,由于∠1=∠2=30°,则∠1=∠BCD=30°,可判断DG∥BC,利用平行线的性质得∠3=∠ACB=∠4+∠BCD,所以∠4=54°.
解答: 解:∵CD⊥AB,FE⊥AB,
∴∠BEF=∠BDC=90°,
∴FE∥CD,
∴∠2=∠BCD,
∵∠1=∠2=30°,
∴∠1=∠BCD=30°,
∴DG∥BC,
∴∠3=∠ACB=∠4+∠BCD,
∴∠4=84°﹣30°=54°.
点评: 本题考查了平行线的判定与性质:同位角相等,两直线平行;内错角相等,两直线平行;两直线平行,同位角相等.
20.如图,已知DE⊥AC于点E,BC⊥AC于点C,FG⊥AB于点G,∠1=∠2,求证:CD⊥AB.
考点: 平行线的判定与性质.
专题: 证明题.
分析: 根据垂直于同一直线的两直线互相平行可得DE∥BC,再根据两直线平行,内错角相等可得∠2=∠3,然后求出∠1=∠3,根据同位角相等两直线平行可得GF∥CD,再根据垂直于同一直线的两直线互相平行证明.
解答: 证明:∵DE⊥AC,BC⊥AC,
∴DE∥BC,
∴∠2=∠3,
∵∠1=∠2,
∴∠1=∠3,
∴GF∥CD,
∵FG⊥AB,
∴CD⊥AB.
点评: 本题考查了平行线的判定与性质,垂直于同一直线的两直线平行,熟记性质是解题的关键.
21.如图,已知AB∥CD,被直线EF所截交AB、CD于点M、N,MP平分∠EMB,NQ平分∠MND,证明:MP∥NQ.
考点: 平行线的判定与性质.
专题: 证明题.
分析: 由AB∥CD,根据平行线的性质得∠EMB=∠MND,再根据角平分线的定义得到∠EMP=∠EMB,∠MNQ=∠MND,则∠EMP=∠MNQ,然后根据平行线的判定即可得到MP∥NQ.
解答: 证明:∵AB∥CD,
∴∠EMB=∠MND,
∵N,MP平分∠EMB,NQ平分∠MND,
∴∠EMP=∠EMB,∠MNQ=∠MND,
∴∠EMP=∠MNQ,
∴MP∥NQ.
点评: 本题考查了平行线的判定与性质:两直线平行,同位角相等;同位角相等,两直线平行.
22.如图所示是甲、乙二人在△ABC中的行进路线,甲:B→D→F→E;乙:B→C→E→D.已知∠1+∠2=180°,∠3=∠B.
(1)试判断∠AED与∠ACB的大小关系,并说明理由;
(2)有哪些路线是平行的?
考点: 平行线的判定与性质.
分析: (1)根据“同旁内角互补,两直线平行”推知EF∥AB,则“两直线平行,内错角相等”:∠3=∠5,所以结合已知条件推知∠5=∠B,故DE∥BC,所以∠AED=∠ACB;
(2)由(1)的推理过程来写出图中的平行线.
解答: 解:(1)∠AED=∠ACB.理由如下:
如图,∵∠1+∠2=180°,∠1+∠4=180°,
∴∠2=∠4,
∴EF∥AB,
∴∠3=∠5.
又∵∠3=∠B,
∴DE∥BC,
∴∠AED=∠ACB;
(2)由(1)知,BD与FE平行,BC与ED平行.
点评: 本题考查了平行线的判定与性质.解答此题的关键是注意平行线的性质和判定定理的综合运用.
23.如图所示,如果内错角∠1与∠5相等,那么与∠1相等的角还有吗?与∠1互补的角有吗?如果有,请写出来,并说明你的理由.
考点: 平行线的判定与性质;余角和补角.
分析: 根据平行线的判定定理推知a∥b,则利用平行线的性质和对顶角相等以及等量代换进行解答.
解答: 解:∠1=∠2=∠5,1+∠3=∠1+∠4=180°.
理由如下:
∵内错角∠1与∠5相等,
∴a∥b,
∴∠1=∠2(两直线平行,同位角相等),∠1+∠3=180°(两直线平行,同旁内角互补),
又∵∠2=∠5、∠3=∠4(对顶角相等),
∴∠1=∠2=∠5,1+∠3=∠1+∠4=180°(等量代换).
点评: 本题考查了平行线的判定与性质、余角和补角.利用已知条件判定a∥b是解题的关键.
24.如图,已知AB∥CD,AD∥BC,∠1=∠2,求证:DE∥BF.
考点: 平行线的判定与性质.
专题: 证明题.
分析: 由AB与CD平行,AD与BC平行,得到四边形ABCD为平行四边形,且得到一对内错角相等,根据平行四边形的对边相等得到AD=CB,利用ASA得到三角形ADE与三角形BCF全等,利用全等三角形的对应角相等得到一对角相等,再利用等角的补角相等得到一对内错角相等,利用内错角相等两直线平行即可得证.
解答: 证明:∵AB∥CD,AD∥BC,
∴四边形ABCD为平行四边形,且∠DAE=∠BCF,
∴AD=BC,
在△ADE和△BCF中,
,
∴△ADE≌△BCF(ASA),
∴∠AED=∠CFB,
∵∠AED+∠DEC=180°,∠CFB+∠AFB=180°,
∴∠DEC=∠AFB,
∴DE∥BF.
点评: 此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
