数学人教A版(2019)选择性必修第三册6.2.4组合数 课件(共66张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第三册6.2.4组合数 课件(共66张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-28 17:45:36 | ||
图片预览










文档简介
(共66张PPT)
第6章《计数原理》人教A版2019选择性必修第三册6.2.4 组合数(1)理解组合和组合数的概念,能够区分组合数和组合;
(2)通过探索排列和组合的关系,利用计数原理推导组合数公式;
(3)通过组合数的计算,体会“数学运算”,通过探索排列和组合的关系,体会“逻辑推理”
学习目标
类比排列数,我们引进组合数概念:
环节一:创设情境,引入课题
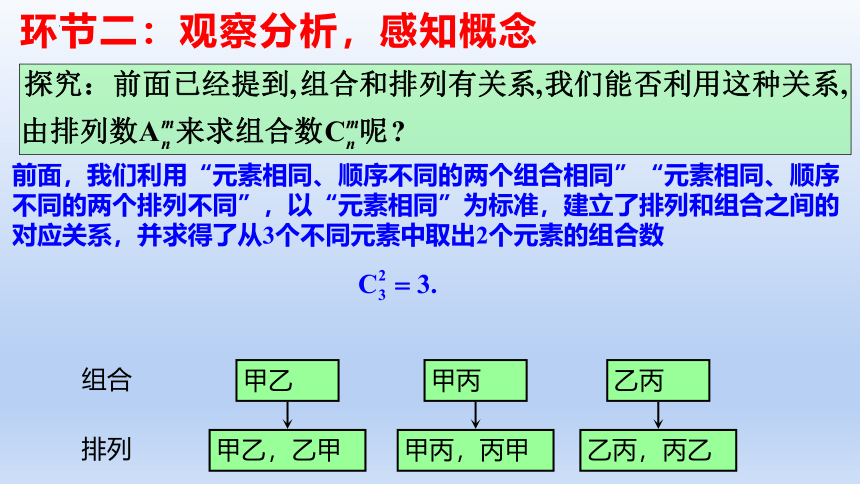
前面,我们利用“元素相同、顺序不同的两个组合相同”“元素相同、顺序不同的两个排列不同”,以“元素相同”为标准,建立了排列和组合之间的对应关系,并求得了从3个不同元素中取出2个元素的组合数
甲乙
甲丙
甲乙,乙甲
甲丙,丙甲
乙丙
乙丙,丙乙
组合
排列
环节二:观察分析,感知概念
a b c
a b c b a c c a b
a c b b c a c b a
a b d
a b d b a d d a b
a d b b d a d b a
a c d
a c d c a d d a c
a d c c d a d c a
b c d
b c d c b d d b c
b d c c d b d c b
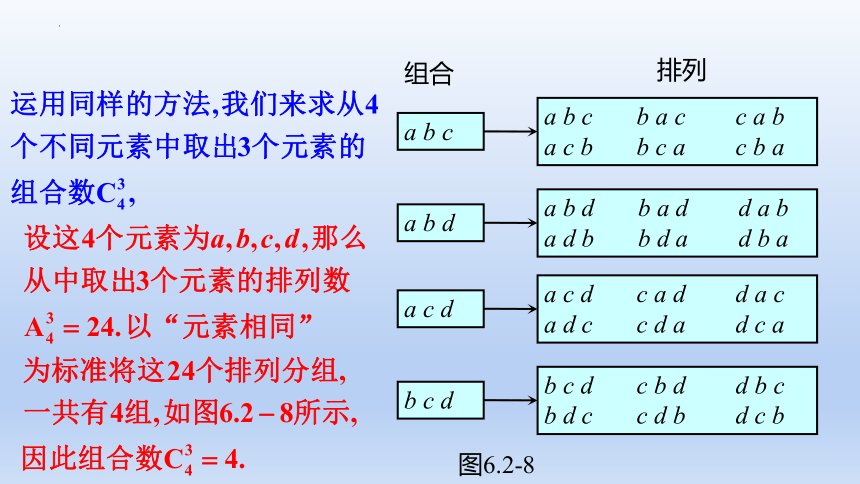
图6.2-8
组合
排列
环节三:抽象概括,形成概念
环节四:辨析理解,深化概念
思考:观察例的(1)与(2),(3)与(4)的结果,你有什么发现
(1)与(2)分别用了不同形式的组合数公式,你对公式的选择有什么想法
例7 在100件产品中,有98件合格品,2件次品、从这100件产品中任意抽出3件.
(1)有多少种不同的抽法
(2)抽出的3件中恰好有1件是次品的抽法有多少种
(3)抽出的3件中至少有1件是次品的抽法有多少种
分析:(1)从100件产品中任意抽出3件,不需考虑顺序,因此这是一个组合问题;
(2)可以先从2件次品中抽出1件,再从98件合格品中抽出2件,因此可以看作是一个分步完成的组合问题;
(3)从100件产品抽出的3件中至少有1件是次品,包括有1件次品和有2件次品的情况,因此可以看作是一个分类完成的组合问题.
环节五:课堂练习,巩固运用
例7 在100件产品中,有98件合格品,2件次品、从这100件产品中任意抽出3件.
(1)有多少种不同的抽法
(2)抽出的3件中恰好有1件是次品的抽法有多少种
(3)抽出的3件中至少有1件是次品的抽法有多少种
例7 在100件产品中,有98件合格品,2件次品、从这100件产品中任意抽出3件.
(3)抽出的3件中至少有1件是次品的抽法有多少种
(3)方法1 从100件产品抽出的3件中至少有1件是次品,包括有1件次品和有2件次品两种情况,因此根据分类加法计数原理,抽出的3件中至少有1件是次品的抽法种数为
方法2抽出的件中至少有件是次品的抽法种数,就是从100件产品中抽出3件的抽法种数减去3件都是合格品的抽法种数,即
1.组合数公式:
2.组合数性质:
3.解决组合问题:
“先分类,后分步”
直接法、间接法
提高分析问题、解决问题的能力,
发展数学运算、逻辑推理、数学建模等核心素养
环节六:归纳总结,反思提升
完成教材:
第26 27页习题6.2
第2,10,12,13,15,16题.
环节七:目标检测,作业布置
1. 先计算,然后用计算器验证结果:
练习第25页
3.有政治、历史、地理、物理、化学、生物这6门学科的学业水平考试成绩,现要从中选3门成绩.
(1)共有多少种不同的选法?
(2)如果物理和化学恰有1门被选,那么共有多少种不同的选法?
(3)如果物理和化学至少有1门被选,那么共有多少种不同的选法.
习题6.2(第26页)
3.壹圆、伍圆、拾圆、贰拾圆的人民币各1张,一共可以组成多少种币值
由于四张人民币的面值都不相同,组成的面值与顺序无关,所以可以分为四类面值,分别由1张、2张、3张、4张人民币组成,共有不同的面值
4.填空:
(1)有三张参观卷,要在5人中确定3人去参观,不同方法的种数是 ;
(2)要从5件不同的礼物中选出3件分送3位同学,不同方法的种数是 ;
(3)5名工人要在3天中各自选择1天休息,不同方法的种数是 ;
(4)集合A有m个元素,集合B有n个元素,从两个集合中各取1个元素,不同方法的种数 是 .
mn
5.一名同学有4本不同的数学书,5本不同的物理书,3本不同的化学书,现要将这些书放在一个单层的书架上.
(1)如果要选其中的6本书放在书架上,那么有多少种不同的放法?
(2)如果要将全部的书放在书架上,且不使同类的书分开,那么有多少种不同的放法?
6.(1)空间有8个点,其中任何4个点不共面,过每3个点作一个平面,一共可以作多少个平面
(2)空间有10个点,其中任何4点不共面,以每4个点为顶点作一个四面体,一共可以作多少个四面体
(1)由“三个不共线的点确定一个平面”,所确定的平面与点的顺序无关,所以共可确定的平面数是
7.在一次考试的选做题部分,要求在第1题的4个小题中选做3个小题,在第2题的3个小题中选做2个小题,在第3题的2个小题中选做1个小题,有多少种不同的选法
9. 学校要安排一场文艺晚会的11个节目的演出顺序,除第1个节目和最后1个节目已确定外,4个音乐节目要求排在第2,5,7,10的位置,3个舞蹈节目要求排在第3,6,9的位置,2个曲艺节目要求排在第4,8的位置,共有多少种不同的排法
10.班上每个小组有12名同学,现要从每个小组选4名同学组成一支代表队,与其他小组进行辩论赛.
(1)每个小组的代表队有多少种选法?
(2)如果还要从选出的同学中指定1名作替补,那么每个小组的代表队有多少种选法?
(3)如果每支代表队还要分别指定第一、二、三、四辩手,那么每个小组的代表队有多少种选法?
10.班上每个小组有12名同学,现要从每个小组选4名同学组成一支代表队,与其他小组进行辩论赛.
(3)如果每支代表队还要分别指定第一、二、三、四辩手,那么每个小组的代表队有多少种选法?
11.一个数阵有m行n列,第一行中的n个数互不相同,其余行都由这n个数以不同的顺序组成.如果任意两行的顺序都不相同,那么m可以取多大的值?
12.(1)从0,2,4,6中任取3个数字,从1,3,5中任取2个数字,一共可以组成多少个没有重复数字的五位数?
(2)由数字0,1,2,3,4,5,6可以组成多少个没有重复数字,并且比500 0000大的正整数.
13.从5名男生和4名女生中选出4人去参加一项创新大赛,问:
(1)如果4人中男生和女生各选2人,有多少种选法
(2)如果男生中的甲与女生中的乙必须在内,有多少种选法
13.从5名男生和4名女生中选出4人去参加一项创新大赛,问:
(3)如果男生中的甲与女生中的乙至少要1人在内,有多少种选法
13.从5名男生和4名女生中选出4人去参加一项创新大赛,问:
(4)如果4人中必须既有男生又有女生,有多少种选法
14.一个宿舍的6名同学被邀请参加一个晚会.
(1)如果必须有人去,去几个人自行决定,有多少种不同的去法?
(2)如果其中甲和乙两位同学要么都去,要么都不去,有多少种去法?
15.从含有3件次品的100件产品中,任意抽取5件进行检验.
(1)抽出的产品都是合格品的抽法有多少种?
(2)抽出的产品中恰好有2件是次品的抽法有多少种?
(3)抽出的产品中至少有2件是次品的抽法有多少种?
(4)抽出的产品中至多有2件是次品的抽法有多少种?
17. 现有五种不同的颜色要对如图形中的四个部分进行着色,要求有公共边的两块不能用同一种颜色,共有几种不同的着色方法
可以按照I,II,III,IV的顺序分别着色:
分别有5,4,3,3种方法,
所以着色种数有
5×4×3×3=180(种).
18.移动互联网给人们的沟通交流带来了方便.某种移动社交软件平台,既可供用户彼此添加“好友”单独交流,又可供多个用户建立一个“群”(“群里”的人彼此不一定是“好友”关系)共同交流.如果某人在平台上发了信息,他的“好友”都可以看到,但“群”里的非“好友”不能看到.现有一个10人的“群”,其中1人在平台上发了一条信息,“群”里有3人说看到了,那么这个“群”里与发信息这人是“好友”关系的情况可能有多少种?
群里有3人看到了,说明发信息这人在群里的“好友”有3~9人,
19. 甲、乙、丙、丁和戊5名学生进行劳动技术比赛,决出第1名到第5名的名次. 甲、乙两名参赛者去询问成绩,回答者对甲说“很遗憾,你和乙都没有得到冠军”;对乙说“你当然不会是最差的”. 从以上回答分析,5人的名次排列有多少种不同情况
组合数的两个性质
在推导性质1时,我们运用了说明组合等式的一个常用而重要的方法,即把等号两边的不同表达式解释为对同一个组合问题的两个不同的计数方案.
你能根据上述思想方法,利用分类加法计数原理,说明下面的组合数性质吗
一、等分组与不等分组问题
EX3 6本不同的书,按下列要求各有多少种不同的选法:
(1)分给甲、乙、丙三人,每人2本;
EX3 6本不同的书,按下列要求各有多少种不同的选法:
(2)分为三份,每份2本;
因此,分为三份,每份2本一共有15种方法
本题是分组中的“等分组”问题.
EX3 6本不同的书,按下列要求各有多少种不同的选法:
(3)分为三份,一份1本,一份2本,一份3本;
(4)分给甲、乙、丙三人,一人1本,一人2本,一人3本;
EX3 6本不同的书,按下列要求各有多少种不同的选法:
(5)将6本书分给甲乙丙三人,甲四本,乙丙各一本;
(6)将6本书分成三堆,一堆四本,其余两堆各一本;
EX3 6本不同的书,按下列要求各有多少种不同的选法:
(7) 分给甲、乙、丙三人,每人至少1本.
(7) 可以分为三类情况
变式:若10本不同的书,分成6:2:2三堆,有多少种分法?
二、不相邻问题用插空法
A
EX5.某学校组织6×100米接力跑比赛,某班级决定派出A,B,C,D,E,F共6位同学参加比赛.在安排这6人的比赛顺序时,要保证:B安排在A之前,D和C的顺序不能相邻.则符合要求的安排种数为( )
A.60 B.120 C.240 D.480
C
EX6.某工厂安排6人负责周一至周六的中午午休值班工作,每天1人,每人值班1天,若甲、乙两人需安排在相邻两天值班,且都不排在周三,则不同的安排方式有( )
A.192种 B.144种 C.96种 D.72种
B
三、相邻问题用捆绑法
四、混合问题,先“组”后“排”
EX7. 对某种产品的6件不同的正品和4件不同的次品,一一进行测试,直到区分出所有次品为止,若所有次品恰好在第5次测试时全部发现,则这样的测试方法有多少种可能?
EX8. 某学习小组有5个男生3个女生,从中选3名男生和1名女生参加三项竞赛活动,每项活动至少有1人参加,则有不同参赛方法______种.
EX9. 3名医生和6名护士被分配到3所学校为学生体检,每校分配1名医生和2名护士,不同的分配方法共有多少种
四、分类组合,隔板处理
EX10. 有10个运动员名额,再分给7个班,每班至少一个, 有多少种分配方案?
因为10个名额没有差别,把它们排成一排. 相邻名额之间形成9个空隙.
在9个空档中选6个位置插个隔板,可把名额分成7份,对应地分给7个班级,每一种插板方法对应一种分法共有___________种分法.
EX11.(1)10个优秀指标分配给6个班级,每个班级至少一个,共有多少种不同的分配方法?
(2)10个优秀指标分配到1、2、 3三个班,若名额数不少于班级序号数,共有多少种不同的分配方法?
EX12.某校高三年级为了解学情和教情,在该年级6个班中选10名学生参加座谈会,要求每班至少派1名学生参加,其中高三(1)班至少派2名学生参加,则不同的选派方式有( )
A.72种 B.60种 C.50种 D.56种
首先需满足高三(1)班选2名学生,其余班级各选1名学生,然后只需分配剩下的3个名额,
D
EX12.某校高三年级为了解学情和教情,在该年级6个班中选10名学生参加座谈会,要求每班至少派1名学生参加,其中高三(1)班至少派2名学生参加,则不同的选派方式有( )
A.72种 B.60种 C.50种 D.56种
D
解法二:隔板法:十个名额,排成一列,产生9个空隙,为保证高三(1)班至少有2名学生参加,第一个空隙不能插入隔板,在剩余的8个空隙中插入5块隔板,分成6组,
第6章《计数原理》人教A版2019选择性必修第三册6.2.4 组合数(1)理解组合和组合数的概念,能够区分组合数和组合;
(2)通过探索排列和组合的关系,利用计数原理推导组合数公式;
(3)通过组合数的计算,体会“数学运算”,通过探索排列和组合的关系,体会“逻辑推理”
学习目标
类比排列数,我们引进组合数概念:
环节一:创设情境,引入课题
前面,我们利用“元素相同、顺序不同的两个组合相同”“元素相同、顺序不同的两个排列不同”,以“元素相同”为标准,建立了排列和组合之间的对应关系,并求得了从3个不同元素中取出2个元素的组合数
甲乙
甲丙
甲乙,乙甲
甲丙,丙甲
乙丙
乙丙,丙乙
组合
排列
环节二:观察分析,感知概念
a b c
a b c b a c c a b
a c b b c a c b a
a b d
a b d b a d d a b
a d b b d a d b a
a c d
a c d c a d d a c
a d c c d a d c a
b c d
b c d c b d d b c
b d c c d b d c b
图6.2-8
组合
排列
环节三:抽象概括,形成概念
环节四:辨析理解,深化概念
思考:观察例的(1)与(2),(3)与(4)的结果,你有什么发现
(1)与(2)分别用了不同形式的组合数公式,你对公式的选择有什么想法
例7 在100件产品中,有98件合格品,2件次品、从这100件产品中任意抽出3件.
(1)有多少种不同的抽法
(2)抽出的3件中恰好有1件是次品的抽法有多少种
(3)抽出的3件中至少有1件是次品的抽法有多少种
分析:(1)从100件产品中任意抽出3件,不需考虑顺序,因此这是一个组合问题;
(2)可以先从2件次品中抽出1件,再从98件合格品中抽出2件,因此可以看作是一个分步完成的组合问题;
(3)从100件产品抽出的3件中至少有1件是次品,包括有1件次品和有2件次品的情况,因此可以看作是一个分类完成的组合问题.
环节五:课堂练习,巩固运用
例7 在100件产品中,有98件合格品,2件次品、从这100件产品中任意抽出3件.
(1)有多少种不同的抽法
(2)抽出的3件中恰好有1件是次品的抽法有多少种
(3)抽出的3件中至少有1件是次品的抽法有多少种
例7 在100件产品中,有98件合格品,2件次品、从这100件产品中任意抽出3件.
(3)抽出的3件中至少有1件是次品的抽法有多少种
(3)方法1 从100件产品抽出的3件中至少有1件是次品,包括有1件次品和有2件次品两种情况,因此根据分类加法计数原理,抽出的3件中至少有1件是次品的抽法种数为
方法2抽出的件中至少有件是次品的抽法种数,就是从100件产品中抽出3件的抽法种数减去3件都是合格品的抽法种数,即
1.组合数公式:
2.组合数性质:
3.解决组合问题:
“先分类,后分步”
直接法、间接法
提高分析问题、解决问题的能力,
发展数学运算、逻辑推理、数学建模等核心素养
环节六:归纳总结,反思提升
完成教材:
第26 27页习题6.2
第2,10,12,13,15,16题.
环节七:目标检测,作业布置
1. 先计算,然后用计算器验证结果:
练习第25页
3.有政治、历史、地理、物理、化学、生物这6门学科的学业水平考试成绩,现要从中选3门成绩.
(1)共有多少种不同的选法?
(2)如果物理和化学恰有1门被选,那么共有多少种不同的选法?
(3)如果物理和化学至少有1门被选,那么共有多少种不同的选法.
习题6.2(第26页)
3.壹圆、伍圆、拾圆、贰拾圆的人民币各1张,一共可以组成多少种币值
由于四张人民币的面值都不相同,组成的面值与顺序无关,所以可以分为四类面值,分别由1张、2张、3张、4张人民币组成,共有不同的面值
4.填空:
(1)有三张参观卷,要在5人中确定3人去参观,不同方法的种数是 ;
(2)要从5件不同的礼物中选出3件分送3位同学,不同方法的种数是 ;
(3)5名工人要在3天中各自选择1天休息,不同方法的种数是 ;
(4)集合A有m个元素,集合B有n个元素,从两个集合中各取1个元素,不同方法的种数 是 .
mn
5.一名同学有4本不同的数学书,5本不同的物理书,3本不同的化学书,现要将这些书放在一个单层的书架上.
(1)如果要选其中的6本书放在书架上,那么有多少种不同的放法?
(2)如果要将全部的书放在书架上,且不使同类的书分开,那么有多少种不同的放法?
6.(1)空间有8个点,其中任何4个点不共面,过每3个点作一个平面,一共可以作多少个平面
(2)空间有10个点,其中任何4点不共面,以每4个点为顶点作一个四面体,一共可以作多少个四面体
(1)由“三个不共线的点确定一个平面”,所确定的平面与点的顺序无关,所以共可确定的平面数是
7.在一次考试的选做题部分,要求在第1题的4个小题中选做3个小题,在第2题的3个小题中选做2个小题,在第3题的2个小题中选做1个小题,有多少种不同的选法
9. 学校要安排一场文艺晚会的11个节目的演出顺序,除第1个节目和最后1个节目已确定外,4个音乐节目要求排在第2,5,7,10的位置,3个舞蹈节目要求排在第3,6,9的位置,2个曲艺节目要求排在第4,8的位置,共有多少种不同的排法
10.班上每个小组有12名同学,现要从每个小组选4名同学组成一支代表队,与其他小组进行辩论赛.
(1)每个小组的代表队有多少种选法?
(2)如果还要从选出的同学中指定1名作替补,那么每个小组的代表队有多少种选法?
(3)如果每支代表队还要分别指定第一、二、三、四辩手,那么每个小组的代表队有多少种选法?
10.班上每个小组有12名同学,现要从每个小组选4名同学组成一支代表队,与其他小组进行辩论赛.
(3)如果每支代表队还要分别指定第一、二、三、四辩手,那么每个小组的代表队有多少种选法?
11.一个数阵有m行n列,第一行中的n个数互不相同,其余行都由这n个数以不同的顺序组成.如果任意两行的顺序都不相同,那么m可以取多大的值?
12.(1)从0,2,4,6中任取3个数字,从1,3,5中任取2个数字,一共可以组成多少个没有重复数字的五位数?
(2)由数字0,1,2,3,4,5,6可以组成多少个没有重复数字,并且比500 0000大的正整数.
13.从5名男生和4名女生中选出4人去参加一项创新大赛,问:
(1)如果4人中男生和女生各选2人,有多少种选法
(2)如果男生中的甲与女生中的乙必须在内,有多少种选法
13.从5名男生和4名女生中选出4人去参加一项创新大赛,问:
(3)如果男生中的甲与女生中的乙至少要1人在内,有多少种选法
13.从5名男生和4名女生中选出4人去参加一项创新大赛,问:
(4)如果4人中必须既有男生又有女生,有多少种选法
14.一个宿舍的6名同学被邀请参加一个晚会.
(1)如果必须有人去,去几个人自行决定,有多少种不同的去法?
(2)如果其中甲和乙两位同学要么都去,要么都不去,有多少种去法?
15.从含有3件次品的100件产品中,任意抽取5件进行检验.
(1)抽出的产品都是合格品的抽法有多少种?
(2)抽出的产品中恰好有2件是次品的抽法有多少种?
(3)抽出的产品中至少有2件是次品的抽法有多少种?
(4)抽出的产品中至多有2件是次品的抽法有多少种?
17. 现有五种不同的颜色要对如图形中的四个部分进行着色,要求有公共边的两块不能用同一种颜色,共有几种不同的着色方法
可以按照I,II,III,IV的顺序分别着色:
分别有5,4,3,3种方法,
所以着色种数有
5×4×3×3=180(种).
18.移动互联网给人们的沟通交流带来了方便.某种移动社交软件平台,既可供用户彼此添加“好友”单独交流,又可供多个用户建立一个“群”(“群里”的人彼此不一定是“好友”关系)共同交流.如果某人在平台上发了信息,他的“好友”都可以看到,但“群”里的非“好友”不能看到.现有一个10人的“群”,其中1人在平台上发了一条信息,“群”里有3人说看到了,那么这个“群”里与发信息这人是“好友”关系的情况可能有多少种?
群里有3人看到了,说明发信息这人在群里的“好友”有3~9人,
19. 甲、乙、丙、丁和戊5名学生进行劳动技术比赛,决出第1名到第5名的名次. 甲、乙两名参赛者去询问成绩,回答者对甲说“很遗憾,你和乙都没有得到冠军”;对乙说“你当然不会是最差的”. 从以上回答分析,5人的名次排列有多少种不同情况
组合数的两个性质
在推导性质1时,我们运用了说明组合等式的一个常用而重要的方法,即把等号两边的不同表达式解释为对同一个组合问题的两个不同的计数方案.
你能根据上述思想方法,利用分类加法计数原理,说明下面的组合数性质吗
一、等分组与不等分组问题
EX3 6本不同的书,按下列要求各有多少种不同的选法:
(1)分给甲、乙、丙三人,每人2本;
EX3 6本不同的书,按下列要求各有多少种不同的选法:
(2)分为三份,每份2本;
因此,分为三份,每份2本一共有15种方法
本题是分组中的“等分组”问题.
EX3 6本不同的书,按下列要求各有多少种不同的选法:
(3)分为三份,一份1本,一份2本,一份3本;
(4)分给甲、乙、丙三人,一人1本,一人2本,一人3本;
EX3 6本不同的书,按下列要求各有多少种不同的选法:
(5)将6本书分给甲乙丙三人,甲四本,乙丙各一本;
(6)将6本书分成三堆,一堆四本,其余两堆各一本;
EX3 6本不同的书,按下列要求各有多少种不同的选法:
(7) 分给甲、乙、丙三人,每人至少1本.
(7) 可以分为三类情况
变式:若10本不同的书,分成6:2:2三堆,有多少种分法?
二、不相邻问题用插空法
A
EX5.某学校组织6×100米接力跑比赛,某班级决定派出A,B,C,D,E,F共6位同学参加比赛.在安排这6人的比赛顺序时,要保证:B安排在A之前,D和C的顺序不能相邻.则符合要求的安排种数为( )
A.60 B.120 C.240 D.480
C
EX6.某工厂安排6人负责周一至周六的中午午休值班工作,每天1人,每人值班1天,若甲、乙两人需安排在相邻两天值班,且都不排在周三,则不同的安排方式有( )
A.192种 B.144种 C.96种 D.72种
B
三、相邻问题用捆绑法
四、混合问题,先“组”后“排”
EX7. 对某种产品的6件不同的正品和4件不同的次品,一一进行测试,直到区分出所有次品为止,若所有次品恰好在第5次测试时全部发现,则这样的测试方法有多少种可能?
EX8. 某学习小组有5个男生3个女生,从中选3名男生和1名女生参加三项竞赛活动,每项活动至少有1人参加,则有不同参赛方法______种.
EX9. 3名医生和6名护士被分配到3所学校为学生体检,每校分配1名医生和2名护士,不同的分配方法共有多少种
四、分类组合,隔板处理
EX10. 有10个运动员名额,再分给7个班,每班至少一个, 有多少种分配方案?
因为10个名额没有差别,把它们排成一排. 相邻名额之间形成9个空隙.
在9个空档中选6个位置插个隔板,可把名额分成7份,对应地分给7个班级,每一种插板方法对应一种分法共有___________种分法.
EX11.(1)10个优秀指标分配给6个班级,每个班级至少一个,共有多少种不同的分配方法?
(2)10个优秀指标分配到1、2、 3三个班,若名额数不少于班级序号数,共有多少种不同的分配方法?
EX12.某校高三年级为了解学情和教情,在该年级6个班中选10名学生参加座谈会,要求每班至少派1名学生参加,其中高三(1)班至少派2名学生参加,则不同的选派方式有( )
A.72种 B.60种 C.50种 D.56种
首先需满足高三(1)班选2名学生,其余班级各选1名学生,然后只需分配剩下的3个名额,
D
EX12.某校高三年级为了解学情和教情,在该年级6个班中选10名学生参加座谈会,要求每班至少派1名学生参加,其中高三(1)班至少派2名学生参加,则不同的选派方式有( )
A.72种 B.60种 C.50种 D.56种
D
解法二:隔板法:十个名额,排成一列,产生9个空隙,为保证高三(1)班至少有2名学生参加,第一个空隙不能插入隔板,在剩余的8个空隙中插入5块隔板,分成6组,
