数学人教A版(2019)选择性必修第三册6.3.2二项式系数的性质 课件(共44张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第三册6.3.2二项式系数的性质 课件(共44张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-29 07:24:20 | ||
图片预览








文档简介
(共44张PPT)
第6章《计数原理》人教A版2019选择性必修第三册6.3.2 二项式系数的性质1.理解二项式系数的性质.
2.会用赋值法求展开式系数的和.
学习目标
同学们根据二项式定理写出(a+b)n(n=1,2,3,4,5,6)的二项式系数.可以写成如下形式:
环节一:创设情境,引入课题
这个表在我国宋代数学家杨辉1261年所著的《详解九章算法》一书里就出现了,所不同的只是这里的表是用阿拉伯数字表示,在那本书里用汉字表示的,这个表称为“杨辉三角”.在欧洲,这个表被认为是法国数学家帕斯卡发现的,杨辉三角的发现比欧洲早500年左右,由此可见我国古代在数学方面的成就.
问题 你能利用上述规律写出下一行的数值吗?
提示 根据规律下一行的数值分别是:1 7 21 35 35 21 7 1.
n (a+b)n的展开式的二项式系数 1
2
3
4
5
6
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
环节二:观察分析,感知概念
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
通过计算、填表,你发现了什么规律?
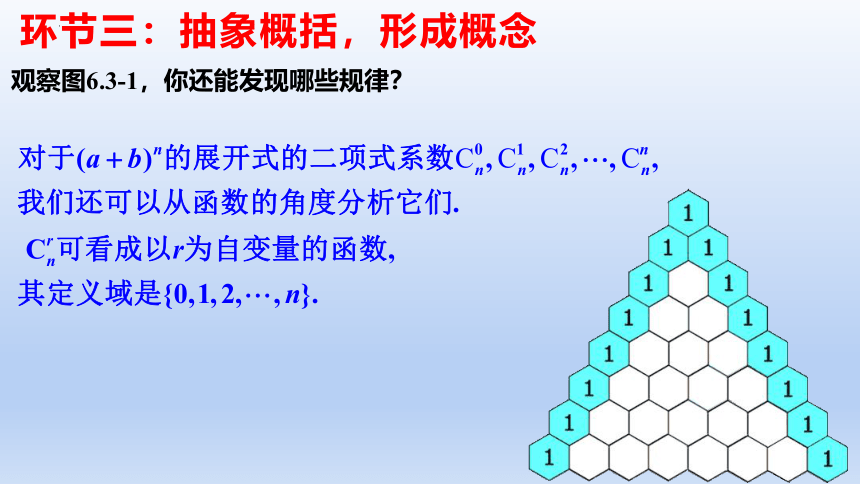
从表6.3-1可以发现,每一行中的系数具有对称性.除此以外还有什么规律呢?为了便于发现规律,上表还可以写成如图6.3-1所示的形式.
………………………………
……………………………
…………………………
………………………
…………………
………………
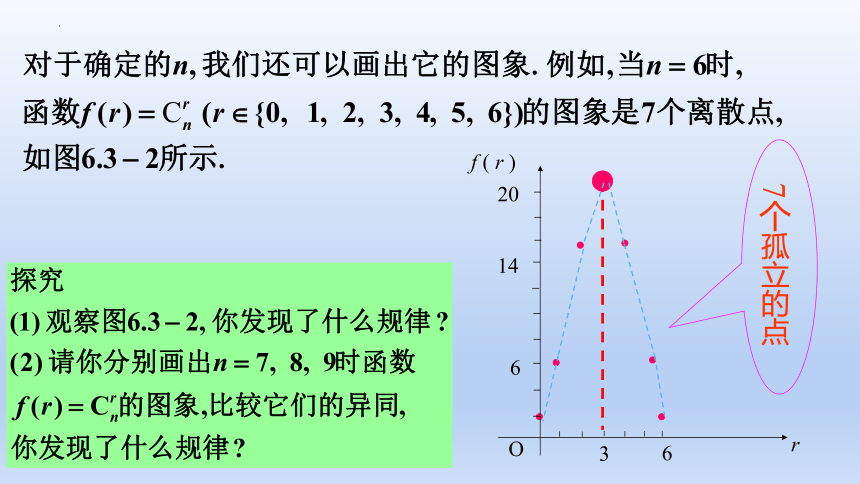
观察图6.3-1,你还能发现哪些规律?
环节三:抽象概括,形成概念
7个孤立的点
O
r
f ( r )
6
3
6
14
20
f(r)
n为奇数;
如n=7
20
10
30
35
O
n
7
4
3
f(r)
r
n
O
6
15
20
1
n为偶数;如n=6
环节四:辨析理解,深化概念
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
……
和为
2
4
8
16
32
64
3.各二项式系数的和
环节五:课堂练习,巩固运用
《详解九章算法》记载的表
杨辉 三角
杨辉
以上二项式系数表,早在我 国南宋数学家杨辉1261年所著的《详解九章算法》一书里就已经出现了,这个表称为杨辉三角,杨辉指出这个方法出于《释锁》算书,且我国北宋数学家贾宪(约公元11世纪)已经用过它。这表明我国发现这个表不晚于11世纪。杨辉三角的发现要比欧洲早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的。
杨辉三角中的斐波那契数列
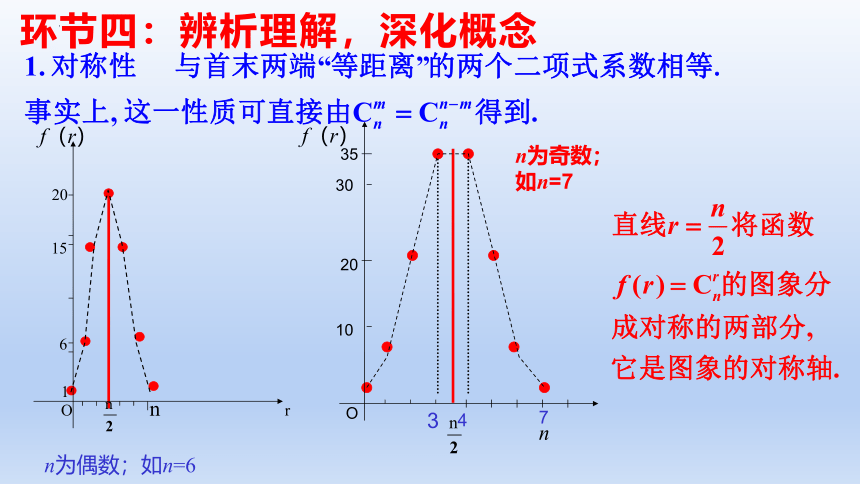
1. 对称性:
二项式系数有以下性质:
与首末两端“等距离”的两个二项式系数相等.
这一性质可直接由公式 得到.
2. 增减性与最大值
环节六:归纳总结,反思提升
环节七:目标检测,作业布置完成教材:教材第34页练习第1,2,3,4题.练习 第34页
1024
3.写出n从1到10的二项式系数表.
4.若一个集合含有n个元素,则这个集合共有多少个子集?
对于集合中的任意一个元素,它与子集的关系都有且仅有两种选择:“属于”与“不属于”,由分步乘法计数原理,集合中的n个元素在子集中的情况共有2n种,故这个集合共有2n个子集.
B
60
习题6.3(第34页)
D
B
0
11.下图反映了二项式定理产生、完备和推广所走过的漫长历程:
第6章《计数原理》人教A版2019选择性必修第三册6.3.2 二项式系数的性质1.理解二项式系数的性质.
2.会用赋值法求展开式系数的和.
学习目标
同学们根据二项式定理写出(a+b)n(n=1,2,3,4,5,6)的二项式系数.可以写成如下形式:
环节一:创设情境,引入课题
这个表在我国宋代数学家杨辉1261年所著的《详解九章算法》一书里就出现了,所不同的只是这里的表是用阿拉伯数字表示,在那本书里用汉字表示的,这个表称为“杨辉三角”.在欧洲,这个表被认为是法国数学家帕斯卡发现的,杨辉三角的发现比欧洲早500年左右,由此可见我国古代在数学方面的成就.
问题 你能利用上述规律写出下一行的数值吗?
提示 根据规律下一行的数值分别是:1 7 21 35 35 21 7 1.
n (a+b)n的展开式的二项式系数 1
2
3
4
5
6
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
环节二:观察分析,感知概念
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
通过计算、填表,你发现了什么规律?
从表6.3-1可以发现,每一行中的系数具有对称性.除此以外还有什么规律呢?为了便于发现规律,上表还可以写成如图6.3-1所示的形式.
………………………………
……………………………
…………………………
………………………
…………………
………………
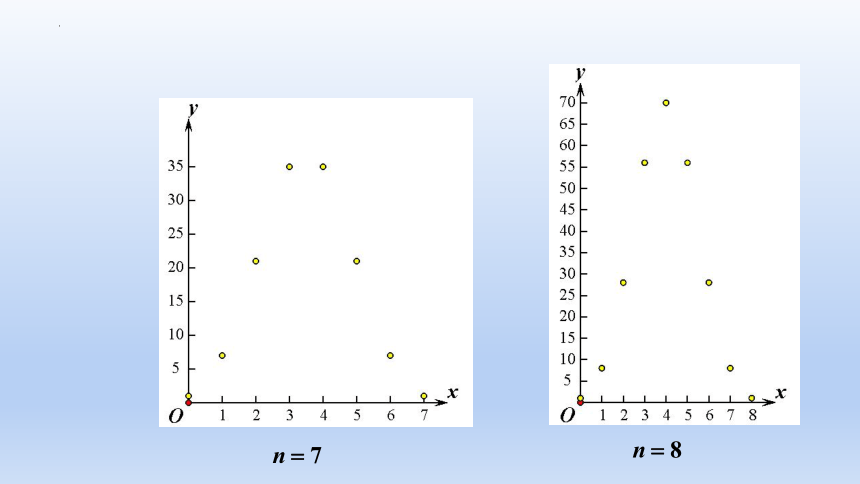
观察图6.3-1,你还能发现哪些规律?
环节三:抽象概括,形成概念
7个孤立的点
O
r
f ( r )
6
3
6
14
20
f(r)
n为奇数;
如n=7
20
10
30
35
O
n
7
4
3
f(r)
r
n
O
6
15
20
1
n为偶数;如n=6
环节四:辨析理解,深化概念
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
……
和为
2
4
8
16
32
64
3.各二项式系数的和
环节五:课堂练习,巩固运用
《详解九章算法》记载的表
杨辉 三角
杨辉
以上二项式系数表,早在我 国南宋数学家杨辉1261年所著的《详解九章算法》一书里就已经出现了,这个表称为杨辉三角,杨辉指出这个方法出于《释锁》算书,且我国北宋数学家贾宪(约公元11世纪)已经用过它。这表明我国发现这个表不晚于11世纪。杨辉三角的发现要比欧洲早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的。
杨辉三角中的斐波那契数列
1. 对称性:
二项式系数有以下性质:
与首末两端“等距离”的两个二项式系数相等.
这一性质可直接由公式 得到.
2. 增减性与最大值
环节六:归纳总结,反思提升
环节七:目标检测,作业布置完成教材:教材第34页练习第1,2,3,4题.练习 第34页
1024
3.写出n从1到10的二项式系数表.
4.若一个集合含有n个元素,则这个集合共有多少个子集?
对于集合中的任意一个元素,它与子集的关系都有且仅有两种选择:“属于”与“不属于”,由分步乘法计数原理,集合中的n个元素在子集中的情况共有2n种,故这个集合共有2n个子集.
B
60
习题6.3(第34页)
D
B
0
11.下图反映了二项式定理产生、完备和推广所走过的漫长历程:
