数学人教A版(2019)选择性必修第三册第六章 计数原理 单元复习课件(共84张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第三册第六章 计数原理 单元复习课件(共84张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-29 07:27:04 | ||
图片预览








文档简介
(共84张PPT)
人教版 高中数学选择性必修三
第六章 《计数原理》
单元复习课件
二、本章常见考点分析
CONTENTS
01
专题一、计数原理
02
专题二、排列及排列数
03
专题三、 组合及组合数
04
专题四、排列组合的综合运用
05
专题五、 二项式定理
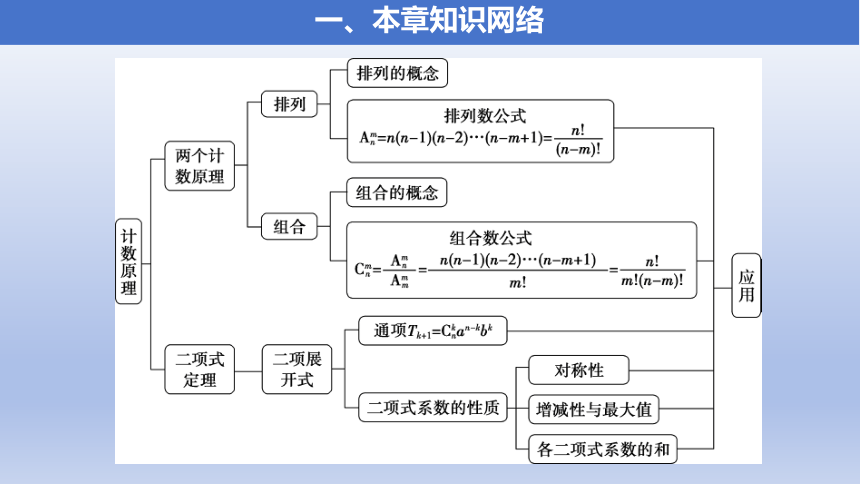
一、本章知识网络
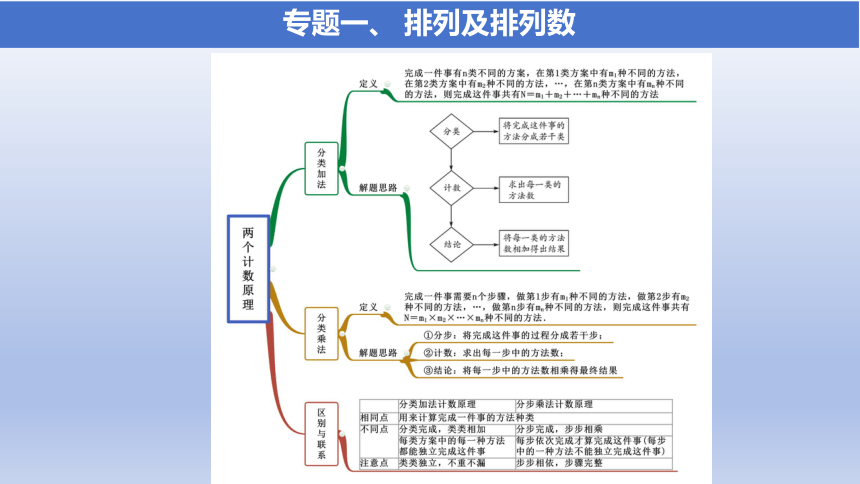
专题一、 排列及排列数
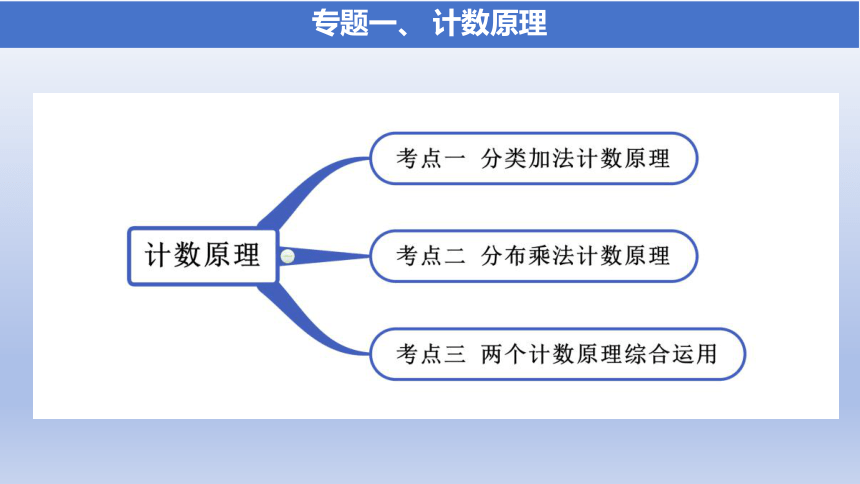
专题一、 计数原理
专题一、 计数原理
专题一、 计数原理
专题一、 计数原理
专题一、 计数原理
专题一、 计数原理
专题一、 计数原理
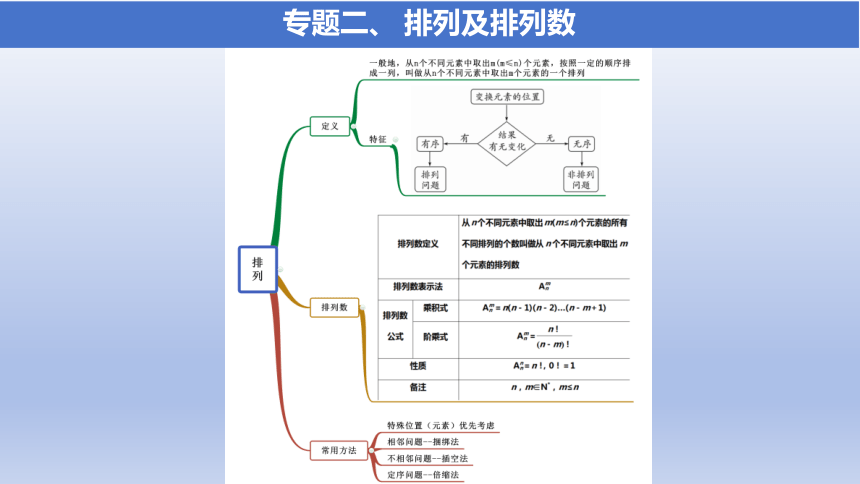
专题二、 排列及排列数
专题二、 排列及排列数
专题二、 排列及排列数
专题二、 排列及排列数
专题二、 排列及排列数
专题二、 排列及排列数
专题二、 排列及排列数
专题二、 排列及排列数
专题二、 排列及排列数
专题二、 排列及排列数
专题二、 排列及排列数
专题三、 组合及组合数
专题三、 组合及组合数
专题三、 组合及组合数
专题三、 组合及组合数
专题三、 组合及组合数
专题三、 组合及组合数
专题三、 组合及组合数
专题三、 组合及组合数
专题三、 组合及组合数
专题三、 组合及组合数
专题三、 组合及组合数
专题四、 排列组合的综合运用
专题四、 排列组合的综合运用
专题四、 排列组合的综合运用
专题四、 排列组合的综合运用
专题四、 排列组合的综合运用
专题四、 排列组合的综合运用
专题四、 排列组合的综合运用
专题四、 排列组合的综合运用
专题四、 排列组合的综合运用
专题四、 排列组合的综合运用
专题四、 排列组合的综合运用
专题四、 排列组合的综合运用
专题四、 排列组合的综合运用
专题四、 排列组合的综合运用
专题四、 排列组合的综合运用
专题四、 排列组合的综合运用
专题五、 二项式定理
专题五、 二项式定理
专题五、 二项式定理
专题五、 二项式定理
专题五、 二项式定理
专题五、 二项式定理
专题五、 二项式定理
专题五、 二项式定理
专题五、 二项式定理
专题五、 二项式定理
专题五、 二项式定理
专题五、 二项式定理
专题五、 二项式定理
复习参考题6
(2)学生可从本年级开设的7门选修课中任意选择3门,并从6种课外活动小组中选择2种,不同的选法种数是________;
525
(3)安排6名歌手演出顺序时,要求某歌手不是第一个出场,也不是最后一个出场,不同排法的种数是________;
480
(4)5个人分4张无座足球票,每人至多分1张,而且票必须分完,那么不同分法的种数是________;
5
(5)5名同学去听同时举行的3个课外知识讲座,每名同学可自由选择听其中的1个讲座,不同选择的种数是________;
243
(6)正十二边形的对角线的条数是________;
54
2.一个集合有5个元素.
(1)这个集合的含有3个元素的子集有多少个?
(2)这个集合的子集共有多少个?
6
(2)某班一天上午有4节课,下午有2节课,现要安排该班一天中语文、数学、政治、英语、体育、艺术6堂课的课程表,要求数学课排在上午,体育课排在下午,不同排法种数是________;
192
(3)某人设计的电脑开机密码由2个英文字母后接4个数字组成,且2个英文字母不相同,该密码可能的个数是___________;
650 0000
(4)以正方体的顶点为顶点的三棱锥的个数是________;
A
B
C
D
D1
C1
B1
A1
58
4.(1)平面内有n条直线,其中没有两条平行,也没有三条交于一点,共有多少个交点?
(2)空间有n个平面,其中没有两个互相平行,也没有三个交于一条直线,共有多少条交线?
7.(1)平面内有两组平行线,一组有m条,另一组有n条,这两组平行线相交,可以构成多少个平行四边形?
7.(2)空间有三组平行平面,第一组有m个,第二组有n个,第三组有l个,不同两组的平面都相交,且交线不都平行,可以构成多少个平行六面体?
(2)要构成平行六面体,需要有3组对面分别平行,
8.某种产品的加工需要经过5道工序.
(1)如果其中某道工序不能放在最后,那么有多少种加工顺序?
(2)如果其中某2道工序既不能放在最前,也不能放在最后,那么有多少种加工顺序?
8.某种产品的加工需要经过5道工序.
(3)如果其中某2道工序必须相邻,那么有多少种加工顺序?
(4)如果其中某2道工序不能相邻,那么有多少种加工顺序?
人教版 高中数学选择性必修三
第六章 《计数原理》
单元复习课件
二、本章常见考点分析
CONTENTS
01
专题一、计数原理
02
专题二、排列及排列数
03
专题三、 组合及组合数
04
专题四、排列组合的综合运用
05
专题五、 二项式定理
一、本章知识网络
专题一、 排列及排列数
专题一、 计数原理
专题一、 计数原理
专题一、 计数原理
专题一、 计数原理
专题一、 计数原理
专题一、 计数原理
专题一、 计数原理
专题二、 排列及排列数
专题二、 排列及排列数
专题二、 排列及排列数
专题二、 排列及排列数
专题二、 排列及排列数
专题二、 排列及排列数
专题二、 排列及排列数
专题二、 排列及排列数
专题二、 排列及排列数
专题二、 排列及排列数
专题二、 排列及排列数
专题三、 组合及组合数
专题三、 组合及组合数
专题三、 组合及组合数
专题三、 组合及组合数
专题三、 组合及组合数
专题三、 组合及组合数
专题三、 组合及组合数
专题三、 组合及组合数
专题三、 组合及组合数
专题三、 组合及组合数
专题三、 组合及组合数
专题四、 排列组合的综合运用
专题四、 排列组合的综合运用
专题四、 排列组合的综合运用
专题四、 排列组合的综合运用
专题四、 排列组合的综合运用
专题四、 排列组合的综合运用
专题四、 排列组合的综合运用
专题四、 排列组合的综合运用
专题四、 排列组合的综合运用
专题四、 排列组合的综合运用
专题四、 排列组合的综合运用
专题四、 排列组合的综合运用
专题四、 排列组合的综合运用
专题四、 排列组合的综合运用
专题四、 排列组合的综合运用
专题四、 排列组合的综合运用
专题五、 二项式定理
专题五、 二项式定理
专题五、 二项式定理
专题五、 二项式定理
专题五、 二项式定理
专题五、 二项式定理
专题五、 二项式定理
专题五、 二项式定理
专题五、 二项式定理
专题五、 二项式定理
专题五、 二项式定理
专题五、 二项式定理
专题五、 二项式定理
复习参考题6
(2)学生可从本年级开设的7门选修课中任意选择3门,并从6种课外活动小组中选择2种,不同的选法种数是________;
525
(3)安排6名歌手演出顺序时,要求某歌手不是第一个出场,也不是最后一个出场,不同排法的种数是________;
480
(4)5个人分4张无座足球票,每人至多分1张,而且票必须分完,那么不同分法的种数是________;
5
(5)5名同学去听同时举行的3个课外知识讲座,每名同学可自由选择听其中的1个讲座,不同选择的种数是________;
243
(6)正十二边形的对角线的条数是________;
54
2.一个集合有5个元素.
(1)这个集合的含有3个元素的子集有多少个?
(2)这个集合的子集共有多少个?
6
(2)某班一天上午有4节课,下午有2节课,现要安排该班一天中语文、数学、政治、英语、体育、艺术6堂课的课程表,要求数学课排在上午,体育课排在下午,不同排法种数是________;
192
(3)某人设计的电脑开机密码由2个英文字母后接4个数字组成,且2个英文字母不相同,该密码可能的个数是___________;
650 0000
(4)以正方体的顶点为顶点的三棱锥的个数是________;
A
B
C
D
D1
C1
B1
A1
58
4.(1)平面内有n条直线,其中没有两条平行,也没有三条交于一点,共有多少个交点?
(2)空间有n个平面,其中没有两个互相平行,也没有三个交于一条直线,共有多少条交线?
7.(1)平面内有两组平行线,一组有m条,另一组有n条,这两组平行线相交,可以构成多少个平行四边形?
7.(2)空间有三组平行平面,第一组有m个,第二组有n个,第三组有l个,不同两组的平面都相交,且交线不都平行,可以构成多少个平行六面体?
(2)要构成平行六面体,需要有3组对面分别平行,
8.某种产品的加工需要经过5道工序.
(1)如果其中某道工序不能放在最后,那么有多少种加工顺序?
(2)如果其中某2道工序既不能放在最前,也不能放在最后,那么有多少种加工顺序?
8.某种产品的加工需要经过5道工序.
(3)如果其中某2道工序必须相邻,那么有多少种加工顺序?
(4)如果其中某2道工序不能相邻,那么有多少种加工顺序?
