【核心素养目标】苏科版数学八年级上册1.3 第2课时 探索三角形全等的条件 SAS(二) 课件(共21张PPT)
文档属性
| 名称 | 【核心素养目标】苏科版数学八年级上册1.3 第2课时 探索三角形全等的条件 SAS(二) 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 864.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-29 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
第1章 全等三角形
1.3 探索三角形全等的条件
第2课时 探索三角形全等的条件
——SAS(二)
1.能识别全等三角形是由图形变化所得.
2.能把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等.
◎重点:能运用三角形的平移、旋转发现图形中的全等变化.
◎难点:能把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等.
将图1旋转到图2的位置,此位置关系的两个三角形全等吗?若要用“SAS”证明两个三角形全等需要注意什么?
·导学建议·
通过本节课的学习,让学生体会到全等三角形的变化实则是旋转或平移形成的图形变化.(准备直尺、圆规、纸片)
利用“SAS”证明两个三角形全等(旋转变化全等)
1.阅读课本本课时“例2”中的内容,回答下列问题.
思考 (1)根据上面已证得的两个三角形全等,你能否说明AC∥BD?
(2)想一想证明两直线平行需要什么条件?
(3)从三角形全等中你能得到什么结论?
答:证明两直线平行可以从同位角相等,内错角相等,同旁内角互补这三个方面去进行思考,由全等可知∠D=∠C(或∠A=∠B),可以得到AC∥BD.
·导学建议·
从学生已会解的问题入手,设计问题把条件逐步变化,使问题分析能力的要求越来越高,实质是促使学生主动地从所要得的结论出发,倒推得出这个结论所需要具备什么条件,要具备这些条件,又可以从哪些已知条件推导出……在经历这样一步一推的探索中,学生渐渐掌握运用全等三角形的判定解决基本问题的能力.
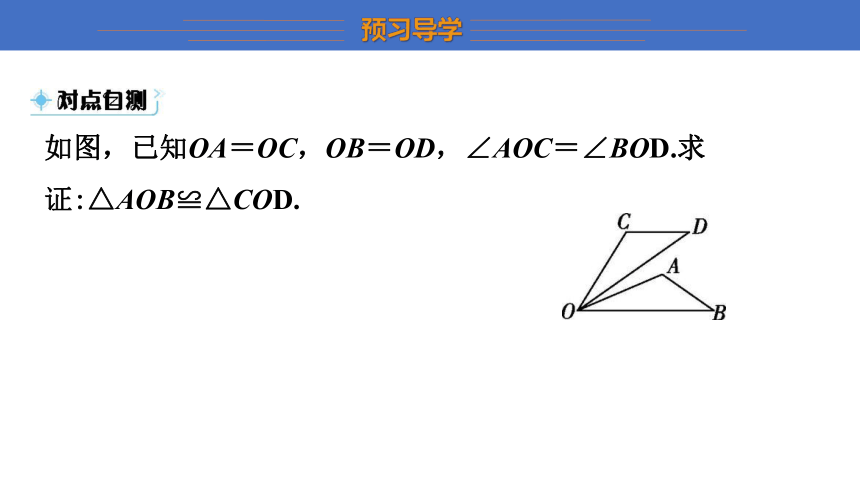
如图,已知OA=OC,OB=OD,∠AOC=∠BOD.求证:△AOB≌△COD.
证明:∵∠AOC=∠BOD,∴∠AOC-∠AOD=∠BOD-∠AOD,即∠COD=∠AOB,
在△AOB和△COD中,,
∴△AOB≌△COD(SAS).
利用“SAS”证明两个三角形全等(旋转平移变化全等)
阅读课本“讨论”及“例3”部分的内容,回答下列问题.
思考 根据例3中的已知条件,你还能证得其他新的结论吗?
(1)想一想由CE=DF可以得到什么结论?
答:(1)由CE=DF可得CF=DE.
(2)由△AEC≌△BFD能得到什么结论?
答:(2)由△AEC≌△BFD可得∠D=∠C,∠A=∠B,AC=BD.
(3)例2图与例3图之间有什么关系?
答:(3)例3图可以通过平移得到例2图.
·导学建议·
(1)例题教学中要提供学生充分讨论和交流的空间,展现学生的思路,通过讨论,引导学生体会推理的思考方法,并由学生自己逐步完善证明过程.(2)教学中要逐步引导学生了解与演绎推理表达形式不同的证明过程.(3)例2和例3的后面都设计了这个例题的拓展延伸,教学中要引导学生主动得到更多的结论,让学生的发散性思维得到发展.
归纳总结 一个三角形经过平移或旋转或翻折的图形变换,变换后的三角形与原三角形 全等 ,全等三角形也常在这些题型中考查到.
全等
如图,已知AB=DC,AB∥CD,E,F是AC上两点,且AF=CE.求证:△ABE≌△CDF.
证明:∵AB∥CD,∴∠A=∠DCF.∵AF=CE,∴AF-EF=CE-EF,即AE=CF,
在△ABE和△CDF中,,
∴△ABE≌△CDF(SAS).
“SAS”判定的综合运用
1.如图,AD=AE,AB=AC,∠BAC=∠DAE,点B,D,E在同一条直线上,∠1=22°,∠2=30°,则∠3的度数为( B )
A.42° B.52°
C.62° D.72°
B
变式演练 如图,点A在BE上,AD=AE,AB=AC,∠1=∠2=30°,则∠3的度数为 30 度.
方法归纳交流 证明两个三角形全等时,常见的隐含“等角”有(1)对顶角相等;(2)等角加(或减)等角,等角仍相等.
30
“SAS”判定的实际应用
2.在测量一个小口圆形容器的壁厚时,小明用“x型转动钳”按如图所示的方法进行测量,其中OA=OD,OB=OC,测得AB=5厘米,EF=7厘米,则圆形容器的壁厚是( A )
A.1厘米 B.2厘米
C.5厘米 D.7厘米
A
变式演练 如图,小亮要测量水池AB的宽度,但没有足够长的绳子,聪明的他设计了一个方案.请将方案补充完整,并说明方案成立的理由.
(1)方案:先在地上取一个可以直接到达A点和B点的点C;连接BC并延长到点E,使得 BC=EC ,连接AC并延长到D,使得 AC=DC ;连接DE并测量出它的长度,则 DE 的长度就是AB的长度.
解:(1)连接BC并延长到点E,使得BC=EC;连接AC并延长到点D,使得AC=DC;连接DE并测量出它的长度,则DE的长度就是AB的长度.故答案为BC=EC,AC=DC,DE.
(2)证明方案成立的理论依据.
(2)在△ABC和△DEC中,,
∴△ABC≌△DEC(SAS),∴AB=DE.
方法归纳交流 本题考查的是三角形全等在实际问题中的应用,要先结合题干将图形补全,然后根据已知条件证明三角形全等得出答案.
第1章 全等三角形
1.3 探索三角形全等的条件
第2课时 探索三角形全等的条件
——SAS(二)
1.能识别全等三角形是由图形变化所得.
2.能把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等.
◎重点:能运用三角形的平移、旋转发现图形中的全等变化.
◎难点:能把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等.
将图1旋转到图2的位置,此位置关系的两个三角形全等吗?若要用“SAS”证明两个三角形全等需要注意什么?
·导学建议·
通过本节课的学习,让学生体会到全等三角形的变化实则是旋转或平移形成的图形变化.(准备直尺、圆规、纸片)
利用“SAS”证明两个三角形全等(旋转变化全等)
1.阅读课本本课时“例2”中的内容,回答下列问题.
思考 (1)根据上面已证得的两个三角形全等,你能否说明AC∥BD?
(2)想一想证明两直线平行需要什么条件?
(3)从三角形全等中你能得到什么结论?
答:证明两直线平行可以从同位角相等,内错角相等,同旁内角互补这三个方面去进行思考,由全等可知∠D=∠C(或∠A=∠B),可以得到AC∥BD.
·导学建议·
从学生已会解的问题入手,设计问题把条件逐步变化,使问题分析能力的要求越来越高,实质是促使学生主动地从所要得的结论出发,倒推得出这个结论所需要具备什么条件,要具备这些条件,又可以从哪些已知条件推导出……在经历这样一步一推的探索中,学生渐渐掌握运用全等三角形的判定解决基本问题的能力.
如图,已知OA=OC,OB=OD,∠AOC=∠BOD.求证:△AOB≌△COD.
证明:∵∠AOC=∠BOD,∴∠AOC-∠AOD=∠BOD-∠AOD,即∠COD=∠AOB,
在△AOB和△COD中,,
∴△AOB≌△COD(SAS).
利用“SAS”证明两个三角形全等(旋转平移变化全等)
阅读课本“讨论”及“例3”部分的内容,回答下列问题.
思考 根据例3中的已知条件,你还能证得其他新的结论吗?
(1)想一想由CE=DF可以得到什么结论?
答:(1)由CE=DF可得CF=DE.
(2)由△AEC≌△BFD能得到什么结论?
答:(2)由△AEC≌△BFD可得∠D=∠C,∠A=∠B,AC=BD.
(3)例2图与例3图之间有什么关系?
答:(3)例3图可以通过平移得到例2图.
·导学建议·
(1)例题教学中要提供学生充分讨论和交流的空间,展现学生的思路,通过讨论,引导学生体会推理的思考方法,并由学生自己逐步完善证明过程.(2)教学中要逐步引导学生了解与演绎推理表达形式不同的证明过程.(3)例2和例3的后面都设计了这个例题的拓展延伸,教学中要引导学生主动得到更多的结论,让学生的发散性思维得到发展.
归纳总结 一个三角形经过平移或旋转或翻折的图形变换,变换后的三角形与原三角形 全等 ,全等三角形也常在这些题型中考查到.
全等
如图,已知AB=DC,AB∥CD,E,F是AC上两点,且AF=CE.求证:△ABE≌△CDF.
证明:∵AB∥CD,∴∠A=∠DCF.∵AF=CE,∴AF-EF=CE-EF,即AE=CF,
在△ABE和△CDF中,,
∴△ABE≌△CDF(SAS).
“SAS”判定的综合运用
1.如图,AD=AE,AB=AC,∠BAC=∠DAE,点B,D,E在同一条直线上,∠1=22°,∠2=30°,则∠3的度数为( B )
A.42° B.52°
C.62° D.72°
B
变式演练 如图,点A在BE上,AD=AE,AB=AC,∠1=∠2=30°,则∠3的度数为 30 度.
方法归纳交流 证明两个三角形全等时,常见的隐含“等角”有(1)对顶角相等;(2)等角加(或减)等角,等角仍相等.
30
“SAS”判定的实际应用
2.在测量一个小口圆形容器的壁厚时,小明用“x型转动钳”按如图所示的方法进行测量,其中OA=OD,OB=OC,测得AB=5厘米,EF=7厘米,则圆形容器的壁厚是( A )
A.1厘米 B.2厘米
C.5厘米 D.7厘米
A
变式演练 如图,小亮要测量水池AB的宽度,但没有足够长的绳子,聪明的他设计了一个方案.请将方案补充完整,并说明方案成立的理由.
(1)方案:先在地上取一个可以直接到达A点和B点的点C;连接BC并延长到点E,使得 BC=EC ,连接AC并延长到D,使得 AC=DC ;连接DE并测量出它的长度,则 DE 的长度就是AB的长度.
解:(1)连接BC并延长到点E,使得BC=EC;连接AC并延长到点D,使得AC=DC;连接DE并测量出它的长度,则DE的长度就是AB的长度.故答案为BC=EC,AC=DC,DE.
(2)证明方案成立的理论依据.
(2)在△ABC和△DEC中,,
∴△ABC≌△DEC(SAS),∴AB=DE.
方法归纳交流 本题考查的是三角形全等在实际问题中的应用,要先结合题干将图形补全,然后根据已知条件证明三角形全等得出答案.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
