【核心素养目标】苏科版八年级数学上册1.2 全等三角形 课件 (共21张PPT)
文档属性
| 名称 | 【核心素养目标】苏科版八年级数学上册1.2 全等三角形 课件 (共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 714.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-29 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
第1章 全等三角形
1.2 全等三角形
1.能说出全等三角形的概念.能识别全等三角形中的对应边、对应角.
2.会运用全等三角形对应边相等、对应角相等的性质解决问题,并能进行简单的推理和计算.
3.经历三角形平移、翻折、旋转的操作活动,会用图形运动的方法识别复杂图形中的全等三角形.
◎重点:会运用全等三角形对应边相等、对应角相等的性质解决问题,并能进行简单的推理和计算.
◎难点:能够用图形运动的方法识别复杂图形中的全等三角形.
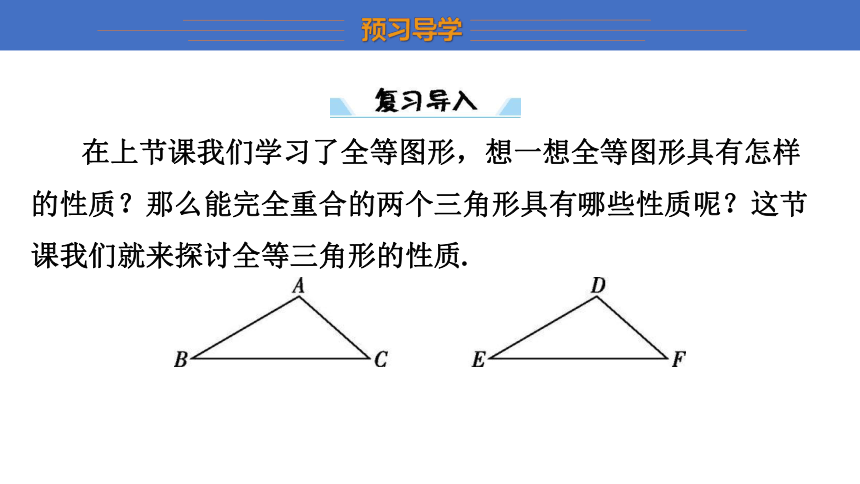
在上节课我们学习了全等图形,想一想全等图形具有怎样的性质?那么能完全重合的两个三角形具有哪些性质呢?这节课我们就来探讨全等三角形的性质.
·导学建议·
回忆旧知,唤醒学生的记忆,从而导入新课.
(准备直尺、白纸)
全等三角形的对应元素
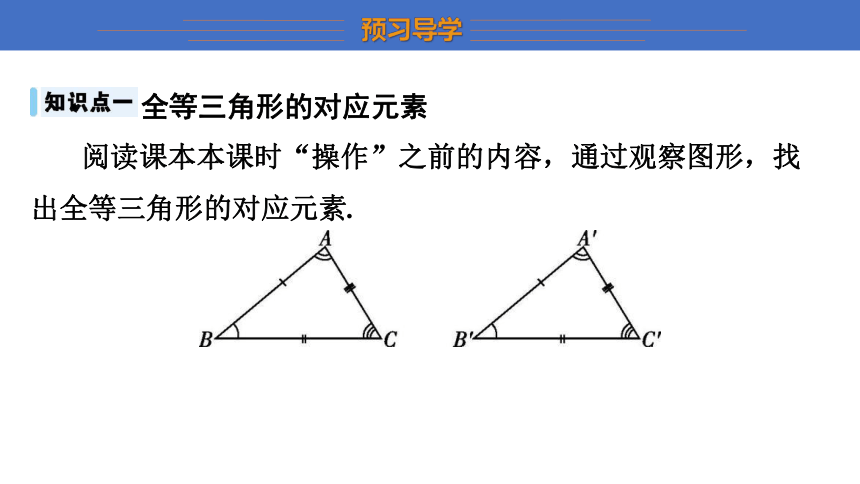
阅读课本本课时“操作”之前的内容,通过观察图形,找出全等三角形的对应元素.
(2)全等三角形有几组对应顶点、有几组对应边、有几组对应角?
(3)对应边之间有什么数量关系呢?对应角呢?
答:(1)图中的两个三角形全等,记作“△ABC≌△A'B'C'”,读作“△ABC全等于△A'B'C'”.表示两个三角形全等时,通常把对应顶点的字母写在对应的位置上.
思考 (1)图中的两个三角形全等吗?若全等,如何用符号表示这两个三角形全等?
(2)全等三角形有3组对应顶点、3组对应边、3组对应角.其中,顶点A和A'、B和B'、C和C'叫做对应顶点.AB和A'B'、BC和B'C'、AC和A'C'叫做对应边.∠A和∠A'、∠B和∠B'、∠C和∠C'叫做对应角.
(3)全等三角形的对应边相等,对应角相等.
归纳总结 两个三角形全等,用“≌”表示,如△ABC≌△A'B'C',读作“△ABC全等于△A'B'C'”,注意对应顶点的字母写在对应的位置上,顺序要一一对应;全等三角形的 对应边 相等, 对应角 相等.
对应边
对应角
已知△ABC≌△DEF,那么∠EDF的对应角是( )
A.∠DEF B.∠BCA
C.∠ABC D.∠BAC
D
探讨全等三角形的性质
阅读课本本课时“操作”和“讨论”部分的内容,体会全等三角形的几种变换形式.
思考 若只改变△ABC的位置,不改变形状和大小,得到△A'B'C',则△ABC与△A'B'C'的位置关系是 .
全等
归纳总结 只改变图形的 位置 ,而不改变其形状、大小的变换叫做全等变换,常见的全等变换有 平移 、 旋转 、 翻折 三种形式.
位置
平移
旋转
翻折
已知图中的两个三角形全等,则∠1等于 60° .
60°
判定两直线平行
1.如图,点A,B,C,D在同一条直线上,△ACE≌△DBF,求证:CE∥BF,AE∥DF.
证明:∵△ACE≌△DBF,∴∠ECA=∠FBD,∠A=∠D,∴CE∥BF,AE∥DF.
方法归纳交流 根据全等三角形对应顶点的字母写在对应位置上,准确找出对应角是解题的关键,在此基础上结合平行线的判定作出判断.
探索角度之间的关系
2.如图,△ADC≌△AFB,∠DAB=20°,DC,BF交于点E.求∠FAC的度数.
解:∵△ADC≌△AFB,∴∠DAC=∠FAB,∴∠DAC-∠BAC=∠FAB-∠BAC,
∴∠FAC=∠DAB=20°.
方法归纳交流 根据三角形全等得出对应角相等是解题的关键.
证明两直线互相垂直
3.如图,△ABD≌△EBC,AB=3 cm,BC=6 cm,
(1)求DE的长.
解:(1)∵△ABD≌△EBC,∴BD=BC=6 cm,BE=AB=3 cm,∴DE=BD-BE=3 cm.
(2)若点A,B,C在同一条直线上,则DB与AC垂直吗?为什么?
解:(2)DB⊥AC.理由如下:∵△ABD≌△EBC,∴∠ABD=∠EBC.又∵∠ABD+∠EBC=180°,∴∠ABD=∠EBC=90°,∴DB⊥AC.
变式演练 如图,已知△ABD≌△CFD,AD⊥BC于点D.
(1)求证:CE⊥AB.
解:(1)证明:∵△ABD≌△CFD,∴∠BAD=∠FCD,又∵∠AFE=∠CFD,∴∠AEF=∠CDF=90°,∴CE⊥AB.
解:(2)∵△ABD≌△CFD,∴AD=DC=5,BD=DF.∵BC=7,∴BD=BC-CD=7-5=2,∴AF=AD-DF=5-2=3.
方法归纳交流 通过全等三角形证明垂直的基本思路是根据“全等三角形对应角相等”,再结合“相等且 互补 的两个角是直角”来判断.
解:(2)∵△ABD≌△CFD,∴AD=DC=5,BD=DF.∵BC
=7,∴BD=BC-CD=7-5=2,∴AF=AD-DF=5-2=3.
互补
(2)已知BC=7,AD=5,求AF的长.
第1章 全等三角形
1.2 全等三角形
1.能说出全等三角形的概念.能识别全等三角形中的对应边、对应角.
2.会运用全等三角形对应边相等、对应角相等的性质解决问题,并能进行简单的推理和计算.
3.经历三角形平移、翻折、旋转的操作活动,会用图形运动的方法识别复杂图形中的全等三角形.
◎重点:会运用全等三角形对应边相等、对应角相等的性质解决问题,并能进行简单的推理和计算.
◎难点:能够用图形运动的方法识别复杂图形中的全等三角形.
在上节课我们学习了全等图形,想一想全等图形具有怎样的性质?那么能完全重合的两个三角形具有哪些性质呢?这节课我们就来探讨全等三角形的性质.
·导学建议·
回忆旧知,唤醒学生的记忆,从而导入新课.
(准备直尺、白纸)
全等三角形的对应元素
阅读课本本课时“操作”之前的内容,通过观察图形,找出全等三角形的对应元素.
(2)全等三角形有几组对应顶点、有几组对应边、有几组对应角?
(3)对应边之间有什么数量关系呢?对应角呢?
答:(1)图中的两个三角形全等,记作“△ABC≌△A'B'C'”,读作“△ABC全等于△A'B'C'”.表示两个三角形全等时,通常把对应顶点的字母写在对应的位置上.
思考 (1)图中的两个三角形全等吗?若全等,如何用符号表示这两个三角形全等?
(2)全等三角形有3组对应顶点、3组对应边、3组对应角.其中,顶点A和A'、B和B'、C和C'叫做对应顶点.AB和A'B'、BC和B'C'、AC和A'C'叫做对应边.∠A和∠A'、∠B和∠B'、∠C和∠C'叫做对应角.
(3)全等三角形的对应边相等,对应角相等.
归纳总结 两个三角形全等,用“≌”表示,如△ABC≌△A'B'C',读作“△ABC全等于△A'B'C'”,注意对应顶点的字母写在对应的位置上,顺序要一一对应;全等三角形的 对应边 相等, 对应角 相等.
对应边
对应角
已知△ABC≌△DEF,那么∠EDF的对应角是( )
A.∠DEF B.∠BCA
C.∠ABC D.∠BAC
D
探讨全等三角形的性质
阅读课本本课时“操作”和“讨论”部分的内容,体会全等三角形的几种变换形式.
思考 若只改变△ABC的位置,不改变形状和大小,得到△A'B'C',则△ABC与△A'B'C'的位置关系是 .
全等
归纳总结 只改变图形的 位置 ,而不改变其形状、大小的变换叫做全等变换,常见的全等变换有 平移 、 旋转 、 翻折 三种形式.
位置
平移
旋转
翻折
已知图中的两个三角形全等,则∠1等于 60° .
60°
判定两直线平行
1.如图,点A,B,C,D在同一条直线上,△ACE≌△DBF,求证:CE∥BF,AE∥DF.
证明:∵△ACE≌△DBF,∴∠ECA=∠FBD,∠A=∠D,∴CE∥BF,AE∥DF.
方法归纳交流 根据全等三角形对应顶点的字母写在对应位置上,准确找出对应角是解题的关键,在此基础上结合平行线的判定作出判断.
探索角度之间的关系
2.如图,△ADC≌△AFB,∠DAB=20°,DC,BF交于点E.求∠FAC的度数.
解:∵△ADC≌△AFB,∴∠DAC=∠FAB,∴∠DAC-∠BAC=∠FAB-∠BAC,
∴∠FAC=∠DAB=20°.
方法归纳交流 根据三角形全等得出对应角相等是解题的关键.
证明两直线互相垂直
3.如图,△ABD≌△EBC,AB=3 cm,BC=6 cm,
(1)求DE的长.
解:(1)∵△ABD≌△EBC,∴BD=BC=6 cm,BE=AB=3 cm,∴DE=BD-BE=3 cm.
(2)若点A,B,C在同一条直线上,则DB与AC垂直吗?为什么?
解:(2)DB⊥AC.理由如下:∵△ABD≌△EBC,∴∠ABD=∠EBC.又∵∠ABD+∠EBC=180°,∴∠ABD=∠EBC=90°,∴DB⊥AC.
变式演练 如图,已知△ABD≌△CFD,AD⊥BC于点D.
(1)求证:CE⊥AB.
解:(1)证明:∵△ABD≌△CFD,∴∠BAD=∠FCD,又∵∠AFE=∠CFD,∴∠AEF=∠CDF=90°,∴CE⊥AB.
解:(2)∵△ABD≌△CFD,∴AD=DC=5,BD=DF.∵BC=7,∴BD=BC-CD=7-5=2,∴AF=AD-DF=5-2=3.
方法归纳交流 通过全等三角形证明垂直的基本思路是根据“全等三角形对应角相等”,再结合“相等且 互补 的两个角是直角”来判断.
解:(2)∵△ABD≌△CFD,∴AD=DC=5,BD=DF.∵BC
=7,∴BD=BC-CD=7-5=2,∴AF=AD-DF=5-2=3.
互补
(2)已知BC=7,AD=5,求AF的长.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
