【核心素养目标】 苏科版数学八年级上册1.3 第4课时 探索三角形全等的条件 AAS 课件 (共27张ppt)
文档属性
| 名称 | 【核心素养目标】 苏科版数学八年级上册1.3 第4课时 探索三角形全等的条件 AAS 课件 (共27张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 899.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-29 08:22:18 | ||
图片预览







文档简介
第1章 全等三角形
1.3 探索三角形全等的条件
第4课时 探索三角形全等的条件
—AAS
1.探索全等三角形的判定方法——“角角边”.
2.能熟练运用“角角边”判定方法解决有关问题.
3.注重全等三角形的性质与判定的综合应用,能把证明一对角或线段相等的问题转化为证明它们所在的两个三角形全等.
◎重点:能用全等三角形的判定方法——“角角边”解决问题.
◎难点:能综合应用全等三角形的性质与判定解决有关问题.
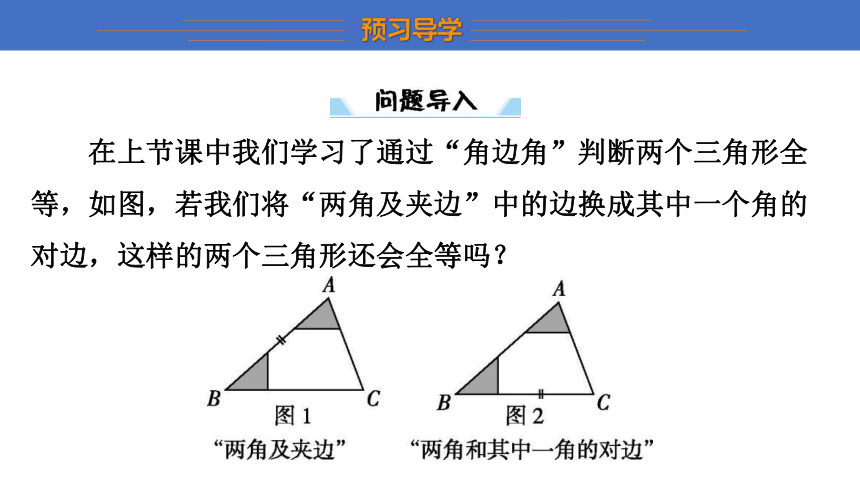
在上节课中我们学习了通过“角边角”判断两个三角形全等,如图,若我们将“两角及夹边”中的边换成其中一个角的对边,这样的两个三角形还会全等吗?
·导学建议·
设置这样的问题是想让学生从三角形的内角和为180°进行转换,得出两个三角形的第三个角也相等,从而将未知问题转化为已学知识,更有利于学生快速掌握本节课内容.(准备三角板、量角器)
两角分别相等且其中一组等角的对边相等的两个三角形全等?
阅读课本本课时“思考”部分的内容,探讨判定三角形全等的“角角边”条件.
思考 如图,在△ABC和△MNP中,∠A=∠M,∠B=∠N,BC=NP.则△ABC与△MNP
全等吗?为什么?
答:全等.由三角形的内角和定理可知∠C=∠P,根据“ASA”可以证明△ABC≌△MNP.
由此可以得到基本事实(AAS)的推论:两角分别相等且其中一组等角的对边相等的两个三角形全等.
·导学建议·
设计“思考”这个活动的目的是让学生在独立思考的基础上推出判定三角形全等的“角角边”条件.这个判定条件是在5个判定三角形全等的条件中,唯一一个不是由学生通过画图等活动归纳得到的,它是利用基本事实“ASA”和“三角形内角和等于180°”进行演绎推理得到的.教学时要给学生的思考、说理留有足够的时间和空间,让学生理解和掌握这一推理的过程,确认这一结论的合理性和正确性.
归纳总结 两角分别相等且其中一组等角的? 对边 ?相等的两个三角形全等.(可以简写成“? 角角边 ?”或“? AAS ?”)?
对边
角角边
AAS
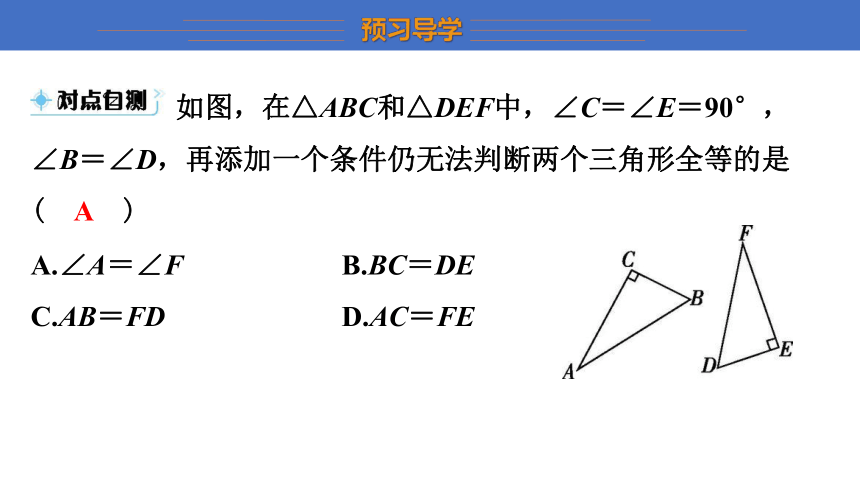
如图,在△ABC和△DEF中,∠C=∠E=90°,∠B=∠D,再添加一个条件仍无法判断两个三角形全等的是
( A )
A.∠A=∠F
B.BC=DE
C.AB=FD
D.AC=FE
A
全等三角形判定的综合运用?
阅读课本“例5”中的内容,掌握全等三角形性质与判定的综合运用.
讨论:如果AD,A'D'分别是△ABC和△A'B'C'的角平分线(或中线),那么AD与A'D'还相等吗?试证明你的结论.
答:AD=A'D'仍成立.理由如下:
如图,
当AD,A'D'分别是△ABC和△A'B'C'的中线时,
BD=CD,B'D'=C'D'.
∵△ABC≌△A'B'C',∴AB=A'B',∠B=∠B',BC=B'C',∴BD=B'D'.
在△ABD和△A'B'D'中,&????????=????′????′,&∠????=∠????′,&????????=????′????′,∴△ABD≌△A'B'D'(SAS),∴AD=A'D'.
?
当AD,A'D'分别是△ABC和△A'B'C'的角平分线时,
∴∠BAD=∠CAD,∠B'A'D'=∠C'A'D'.
∵△ABC≌△A'B'C',∴AB=A'B',∠B=∠B',∠BAC=∠B'A'C',∴∠BAD=∠B'A'D'.
在△ABD和△A'B'D'中,&∠????????????=∠????′????′????′,&????????=????′????′,&∠????=∠????′,
?
∴△ABD≌△A'B'D'(ASA),
∴AD=A'D'.
·导学建议·
例5是推论“AAS”的应用,本例中,条件的变化比例4又进了一步,对问题的分析要求更高.例5的后面设计了这个例题的拓展和延伸探索并证明全等三角形的对应中线、角平分线分别相等.教学中应让学生先经过自己的观察、猜想,再证明,有助于学生不断体会合情推理和演绎推理都是人们探索和认识事物的重要途径.它们相辅相成、密不可分.
证明全等三角形的对应中线相等,是基本事实“SAS”的运用;证明全等三角形的对应的角平分线相等,是基本事实“ASA”的运用.设计例5以及例5的拓展延伸的教学活动,实质是通过多次示范和模仿,既渗透分析的方法,又能帮助学生掌握基本事实“SAS”,“ASA”和推论“AAS”,同时提升他们演绎推理的能力.
如图,点B为AC上一点,AD∥CE,∠ADB=∠CBE,BD=EB.
求证:AC=AD+CE.
证明:∵AD∥CE,∴∠A=∠C.
在△ABD和△CEB中,&∠????=∠????,&∠????????????=∠????????????,&????????=????????,
∴△ABD≌△CEB(AAS),∴AD=BC,AB=CE.
∵AC=AB+BC,∴AC=AD+CE.
?
利用“AAS”判定线段之间的关系
1.如图,在△ABC中,D是BC边的中点,分别过点B,C作BE⊥AD于点E,CF⊥AD交AD的延长线于点F,求证:BE=CF.
证明:∵BE⊥AD,CF⊥AD,
∴∠BED=∠CFD=90°.∵D是BC的中点,∴BD=CD.
在△BDE和△CDF中,&∠????????????=∠????????????,&∠????????????=∠????????????,&????????=????????,
∴△BDE≌△CDF(AAS),∴BE=CF.
?
变式演练 如图,在Rt△ABC中,∠ABC=90°,EF∥BC,PG∥AB,EF=GC,求证:AP=CF.
证明:∵EF∥BC,PG∥AB,∠ABC=90°,∴∠AEF=∠ABC=∠PGC=90°,∠CPG=∠A,
在△AEF和△PGC中,&∠????????????=∠????????????,&∠????????????=∠????,&????????=????????,
∴△AEF≌△PGC(AAS),∴AF=CP,∴AF-PF=CP-PF,∴AP=CF.
?
方法归纳交流 利用全等三角形说明线段或角相等,思路如下:(1)观察要说明的线段或角在哪两个可能全等的三角形中;(2)看准要说明的这两个三角形,看证明它们全等需要的条件中,已知什么,还缺什么;(3)探索、发现及推理所缺条件;(4)因为全等三角形对应角、对应边相等,所以要证明这两个角(或两条边)所在的三角形全等.
利用“AAS”判定三角形全等解决实际问题
2.如图,李华同学用11块高度都是1 cm的相同长方体(除颜色外,其他都相同)小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个正方形ABCD(∠ABC=90°,AB=BC),点B在EF上,点A和C分别与木墙的顶端重合,求两堵木墙之间的距离EF.
解:∵AE⊥EF,CF⊥EF,∴∠AEB=∠BFC=90°,
∴∠EAB+∠ABE=90°.
∵∠ABC=90°,∴∠ABE+∠CBF=90°,∴∠EAB=∠CBF.在△ABE和△BCF中,
&∠????????????=∠????????????,&∠????????????=∠????????????=????????°,&????????=????????,∴△ABE≌△BCF(AAS),
?
∴AE=BF=5 cm,BE=CF=6 cm,
∴EF=5+6=11(cm).
答:两堵木墙之间的距离EF为11 cm.
变式演练 如图,把一个长为10 m的梯子AB斜靠在墙上,测得BM=6 m,梯子沿墙下滑到CD位置,测得∠ABM=∠DCM,DM=8 m,求梯子下滑的高度.
解:∵在△ABM和△DCM中,&∠????????????=∠????????????,&∠????????????=∠????????????,&????????=????????,
?
∴△ABM≌△DCM(AAS),
∴BM=CM=6 m,AM=DM=8 m,
∴AC=AM-CM=2 m.
答:梯子下滑的高度是2 m.
解:∵在△ABM和△DCM中,&∠????????????=∠????????????,&∠????????????=∠????????????,&????????=????????,
?
方法归纳交流 全等三角形在生活中的实际应用,应抓住实际问题不变的量再结合已知条件进行判断两个三角形全等,从而求解.
1.3 探索三角形全等的条件
第4课时 探索三角形全等的条件
—AAS
1.探索全等三角形的判定方法——“角角边”.
2.能熟练运用“角角边”判定方法解决有关问题.
3.注重全等三角形的性质与判定的综合应用,能把证明一对角或线段相等的问题转化为证明它们所在的两个三角形全等.
◎重点:能用全等三角形的判定方法——“角角边”解决问题.
◎难点:能综合应用全等三角形的性质与判定解决有关问题.
在上节课中我们学习了通过“角边角”判断两个三角形全等,如图,若我们将“两角及夹边”中的边换成其中一个角的对边,这样的两个三角形还会全等吗?
·导学建议·
设置这样的问题是想让学生从三角形的内角和为180°进行转换,得出两个三角形的第三个角也相等,从而将未知问题转化为已学知识,更有利于学生快速掌握本节课内容.(准备三角板、量角器)
两角分别相等且其中一组等角的对边相等的两个三角形全等?
阅读课本本课时“思考”部分的内容,探讨判定三角形全等的“角角边”条件.
思考 如图,在△ABC和△MNP中,∠A=∠M,∠B=∠N,BC=NP.则△ABC与△MNP
全等吗?为什么?
答:全等.由三角形的内角和定理可知∠C=∠P,根据“ASA”可以证明△ABC≌△MNP.
由此可以得到基本事实(AAS)的推论:两角分别相等且其中一组等角的对边相等的两个三角形全等.
·导学建议·
设计“思考”这个活动的目的是让学生在独立思考的基础上推出判定三角形全等的“角角边”条件.这个判定条件是在5个判定三角形全等的条件中,唯一一个不是由学生通过画图等活动归纳得到的,它是利用基本事实“ASA”和“三角形内角和等于180°”进行演绎推理得到的.教学时要给学生的思考、说理留有足够的时间和空间,让学生理解和掌握这一推理的过程,确认这一结论的合理性和正确性.
归纳总结 两角分别相等且其中一组等角的? 对边 ?相等的两个三角形全等.(可以简写成“? 角角边 ?”或“? AAS ?”)?
对边
角角边
AAS
如图,在△ABC和△DEF中,∠C=∠E=90°,∠B=∠D,再添加一个条件仍无法判断两个三角形全等的是
( A )
A.∠A=∠F
B.BC=DE
C.AB=FD
D.AC=FE
A
全等三角形判定的综合运用?
阅读课本“例5”中的内容,掌握全等三角形性质与判定的综合运用.
讨论:如果AD,A'D'分别是△ABC和△A'B'C'的角平分线(或中线),那么AD与A'D'还相等吗?试证明你的结论.
答:AD=A'D'仍成立.理由如下:
如图,
当AD,A'D'分别是△ABC和△A'B'C'的中线时,
BD=CD,B'D'=C'D'.
∵△ABC≌△A'B'C',∴AB=A'B',∠B=∠B',BC=B'C',∴BD=B'D'.
在△ABD和△A'B'D'中,&????????=????′????′,&∠????=∠????′,&????????=????′????′,∴△ABD≌△A'B'D'(SAS),∴AD=A'D'.
?
当AD,A'D'分别是△ABC和△A'B'C'的角平分线时,
∴∠BAD=∠CAD,∠B'A'D'=∠C'A'D'.
∵△ABC≌△A'B'C',∴AB=A'B',∠B=∠B',∠BAC=∠B'A'C',∴∠BAD=∠B'A'D'.
在△ABD和△A'B'D'中,&∠????????????=∠????′????′????′,&????????=????′????′,&∠????=∠????′,
?
∴△ABD≌△A'B'D'(ASA),
∴AD=A'D'.
·导学建议·
例5是推论“AAS”的应用,本例中,条件的变化比例4又进了一步,对问题的分析要求更高.例5的后面设计了这个例题的拓展和延伸探索并证明全等三角形的对应中线、角平分线分别相等.教学中应让学生先经过自己的观察、猜想,再证明,有助于学生不断体会合情推理和演绎推理都是人们探索和认识事物的重要途径.它们相辅相成、密不可分.
证明全等三角形的对应中线相等,是基本事实“SAS”的运用;证明全等三角形的对应的角平分线相等,是基本事实“ASA”的运用.设计例5以及例5的拓展延伸的教学活动,实质是通过多次示范和模仿,既渗透分析的方法,又能帮助学生掌握基本事实“SAS”,“ASA”和推论“AAS”,同时提升他们演绎推理的能力.
如图,点B为AC上一点,AD∥CE,∠ADB=∠CBE,BD=EB.
求证:AC=AD+CE.
证明:∵AD∥CE,∴∠A=∠C.
在△ABD和△CEB中,&∠????=∠????,&∠????????????=∠????????????,&????????=????????,
∴△ABD≌△CEB(AAS),∴AD=BC,AB=CE.
∵AC=AB+BC,∴AC=AD+CE.
?
利用“AAS”判定线段之间的关系
1.如图,在△ABC中,D是BC边的中点,分别过点B,C作BE⊥AD于点E,CF⊥AD交AD的延长线于点F,求证:BE=CF.
证明:∵BE⊥AD,CF⊥AD,
∴∠BED=∠CFD=90°.∵D是BC的中点,∴BD=CD.
在△BDE和△CDF中,&∠????????????=∠????????????,&∠????????????=∠????????????,&????????=????????,
∴△BDE≌△CDF(AAS),∴BE=CF.
?
变式演练 如图,在Rt△ABC中,∠ABC=90°,EF∥BC,PG∥AB,EF=GC,求证:AP=CF.
证明:∵EF∥BC,PG∥AB,∠ABC=90°,∴∠AEF=∠ABC=∠PGC=90°,∠CPG=∠A,
在△AEF和△PGC中,&∠????????????=∠????????????,&∠????????????=∠????,&????????=????????,
∴△AEF≌△PGC(AAS),∴AF=CP,∴AF-PF=CP-PF,∴AP=CF.
?
方法归纳交流 利用全等三角形说明线段或角相等,思路如下:(1)观察要说明的线段或角在哪两个可能全等的三角形中;(2)看准要说明的这两个三角形,看证明它们全等需要的条件中,已知什么,还缺什么;(3)探索、发现及推理所缺条件;(4)因为全等三角形对应角、对应边相等,所以要证明这两个角(或两条边)所在的三角形全等.
利用“AAS”判定三角形全等解决实际问题
2.如图,李华同学用11块高度都是1 cm的相同长方体(除颜色外,其他都相同)小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个正方形ABCD(∠ABC=90°,AB=BC),点B在EF上,点A和C分别与木墙的顶端重合,求两堵木墙之间的距离EF.
解:∵AE⊥EF,CF⊥EF,∴∠AEB=∠BFC=90°,
∴∠EAB+∠ABE=90°.
∵∠ABC=90°,∴∠ABE+∠CBF=90°,∴∠EAB=∠CBF.在△ABE和△BCF中,
&∠????????????=∠????????????,&∠????????????=∠????????????=????????°,&????????=????????,∴△ABE≌△BCF(AAS),
?
∴AE=BF=5 cm,BE=CF=6 cm,
∴EF=5+6=11(cm).
答:两堵木墙之间的距离EF为11 cm.
变式演练 如图,把一个长为10 m的梯子AB斜靠在墙上,测得BM=6 m,梯子沿墙下滑到CD位置,测得∠ABM=∠DCM,DM=8 m,求梯子下滑的高度.
解:∵在△ABM和△DCM中,&∠????????????=∠????????????,&∠????????????=∠????????????,&????????=????????,
?
∴△ABM≌△DCM(AAS),
∴BM=CM=6 m,AM=DM=8 m,
∴AC=AM-CM=2 m.
答:梯子下滑的高度是2 m.
解:∵在△ABM和△DCM中,&∠????????????=∠????????????,&∠????????????=∠????????????,&????????=????????,
?
方法归纳交流 全等三角形在生活中的实际应用,应抓住实际问题不变的量再结合已知条件进行判断两个三角形全等,从而求解.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
