6.2.1 向量的加法运算 教案
文档属性
| 名称 | 6.2.1 向量的加法运算 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 434.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-29 00:00:00 | ||
图片预览

文档简介
人教A版必修第二册《 向量的加法运算》
教学内容
平面向量的加法运算,运算规则、几何意义和运算律.
教学目标
1.借助实例和平面向量的几何表示,掌握平面向量加法运算及运算规则,并理解其几何意义.
2.理解平面向量加法运算的运算律和运算性质.
(三)教学重点与难点
重点:向量加法运算的运算法则及其几何意义.
难点:对向量加法运算法则定义的理解.
(四)教学过程设计
【引入新课】
问题1:初中,我们学习过数的运算、代数式的运算,高中我们学习了集合的运算,平面向量,又有哪些运算呢?
答案:向量的运算包括向量的加法运算、向量的减法、数乘运算和向量的数量积运算.
设计意图:通过对这一单元内容的预习,让学生明晰本单元的学习目标,初步搭建平面向量学习内容的框架,对向量的运算有一个初步的认识.
【课堂探究】
问题2:如图所示,假设某人上午从点A到达了点B,下午从点B到达了点C.
(1)分别用向量表示出该人上午的位移、下午的位移以及这一天的位移;
(2)这一天的位移与上午的位移、下午的位移有什么联系?试从大小和方向两个角度加以阐述.
答案:(1)上午的位移是,下午的位移是,一天的位移是.(2)位移可以看成位移与的和.
设计意图:给出了向量加法的实际背景,这说明了研究向量加法的意义及合理性.这一内容的设置,旨在说明从生活中能抽象出数学问题,以此激发学生的学习热情.
引语:而本节课要讲的内容即为向量的加法.(板书:向量的加法)
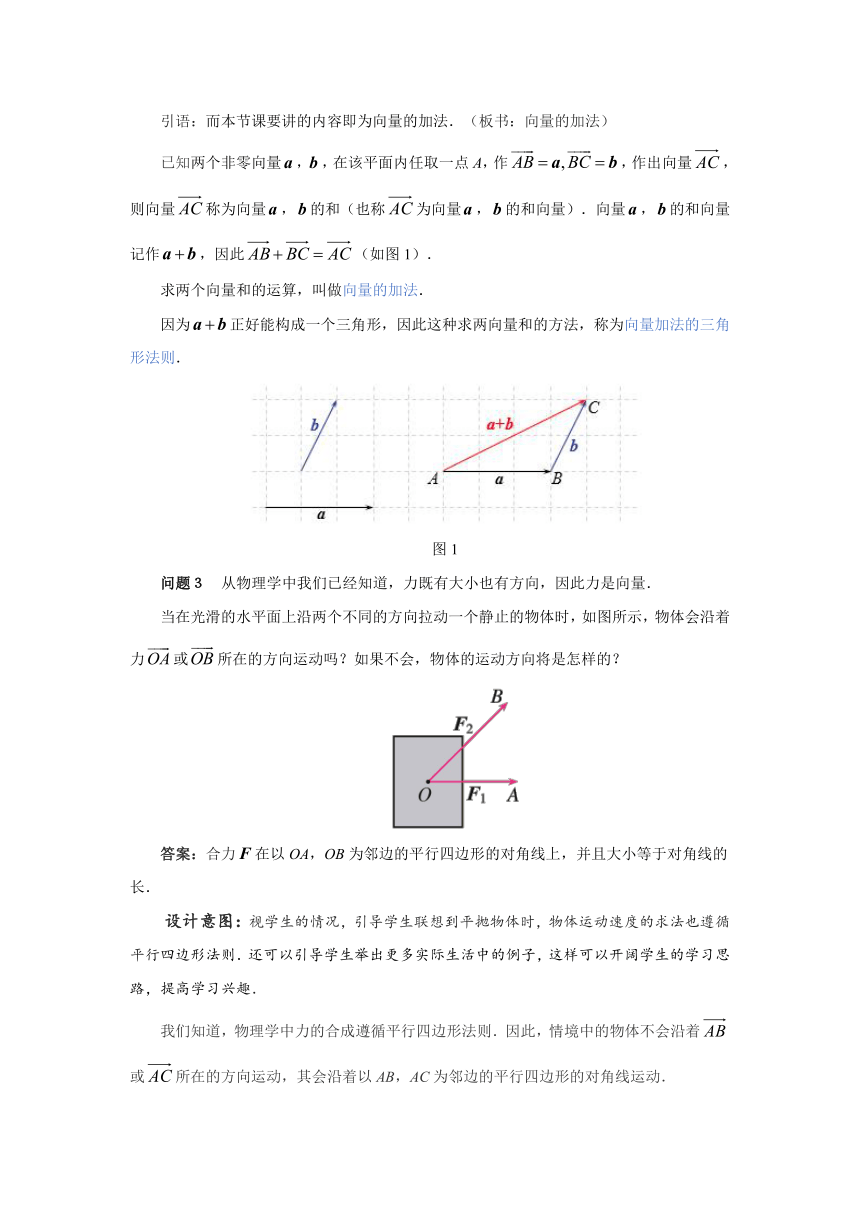
已知两个非零向量,,在该平面内任取一点A,作,作出向量,则向量称为向量,的和(也称为向量,的和向量).向量,的和向量记作,因此(如图1).
求两个向量和的运算,叫做向量的加法.
因为正好能构成一个三角形,因此这种求两向量和的方法,称为向量加法的三角形法则.
图1
问题3 从物理学中我们已经知道,力既有大小也有方向,因此力是向量.
当在光滑的水平面上沿两个不同的方向拉动一个静止的物体时,如图所示,物体会沿着力或所在的方向运动吗?如果不会,物体的运动方向将是怎样的?
答案:合力在以OA,OB为邻边的平行四边形的对角线上,并且大小等于对角线的长.
设计意图:视学生的情况,引导学生联想到平抛物体时,物体运动速度的求法也遵循平行四边形法则.还可以引导学生举出更多实际生活中的例子,这样可以开阔学生的学习思路,提高学习兴趣.
我们知道,物理学中力的合成遵循平行四边形法则.因此,情境中的物体不会沿着或所在的方向运动,其会沿着以AB,AC为邻边的平行四边形的对角线运动.
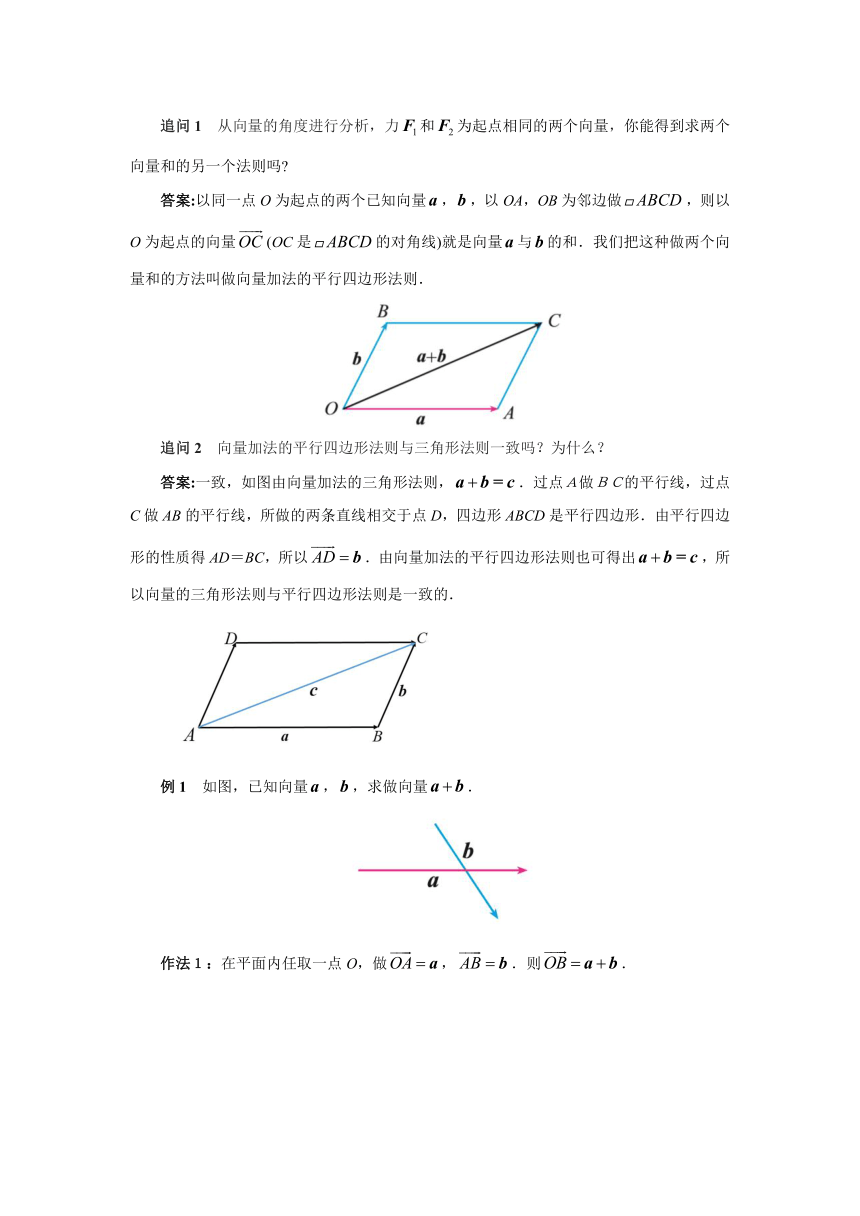
追问1 从向量的角度进行分析,力和为起点相同的两个向量,你能得到求两个向量和的另一个法则吗
答案:以同一点O为起点的两个已知向量,,以OA,OB为邻边做,则以O为起点的向量(OC是的对角线)就是向量与的和.我们把这种做两个向量和的方法叫做向量加法的平行四边形法则.
追问2 向量加法的平行四边形法则与三角形法则一致吗?为什么?
答案:一致,如图由向量加法的三角形法则,.过点A做BC的平行线,过点C做AB的平行线,所做的两条直线相交于点D,四边形ABCD是平行四边形.由平行四边形的性质得AD=BC,所以.由向量加法的平行四边形法则也可得出,所以向量的三角形法则与平行四边形法则是一致的.
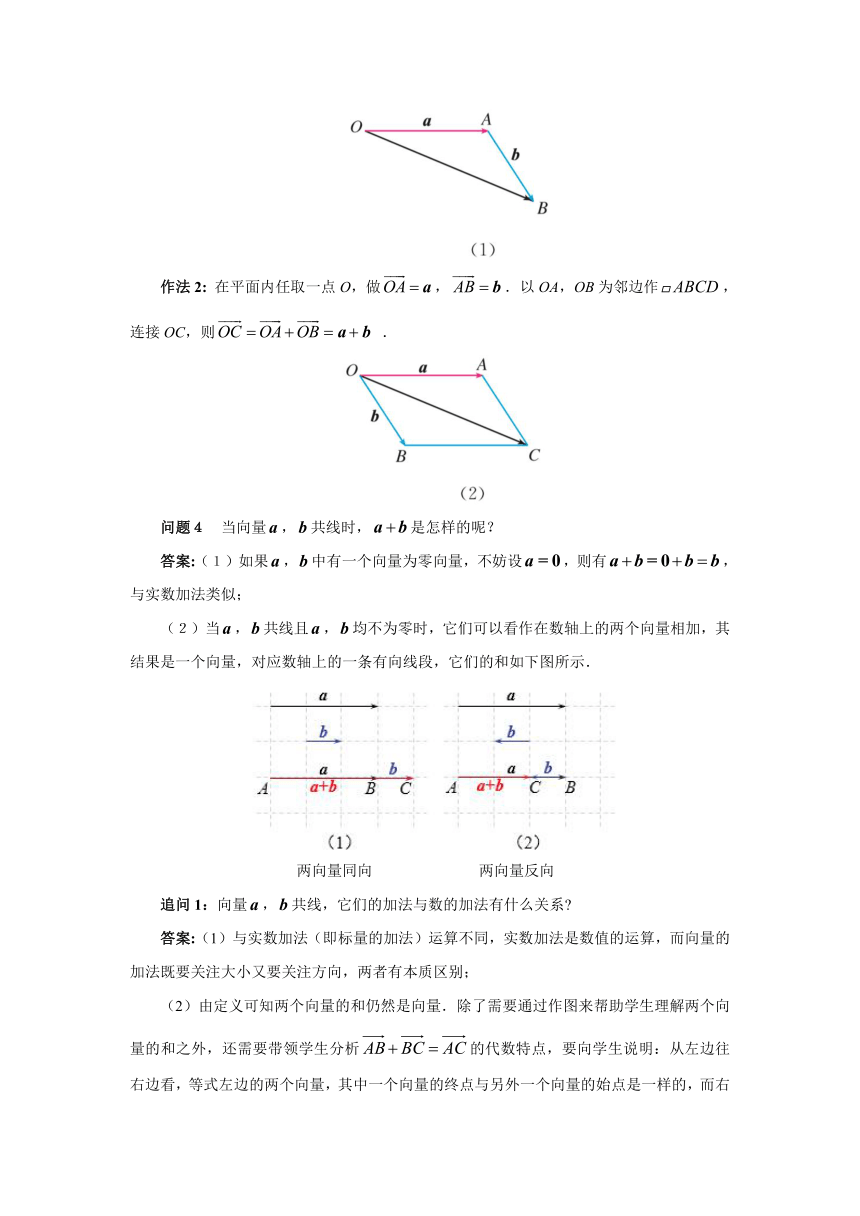
例1 如图,已知向量,,求做向量.
作法1:在平面内任取一点O,做,.则.
作法2: 在平面内任取一点O,做,.以OA,OB为邻边作,连接OC,则 .
问题4 当向量,共线时,是怎样的呢?
答案:(1)如果,中有一个向量为零向量,不妨设,则有,与实数加法类似;
(2)当,共线且,均不为零时,它们可以看作在数轴上的两个向量相加,其结果是一个向量,对应数轴上的一条有向线段,它们的和如下图所示.
两向量同向 两向量反向
追问1:向量,共线,它们的加法与数的加法有什么关系
答案:(1)与实数加法(即标量的加法)运算不同,实数加法是数值的运算,而向量的加法既要关注大小又要关注方向,两者有本质区别;
(2)由定义可知两个向量的和仍然是向量.除了需要通过作图来帮助学生理解两个向量的和之外,还需要带领学生分析的代数特点,要向学生说明:从左边往右边看,等式左边的两个向量,其中一个向量的终点与另外一个向量的始点是一样的,而右边的向量相当于消去了这个点;从右边往左边看,相当于是引入了个新的字母,而且引入的这个新字母是任意的.
(3)容易看出,当向量,共线时,以的终点做为的起点作出,就是连接的起点与的终点的向量(即首尾相接,再首尾相连) ,此时也符合向量加法的三角形法则.
追问2:结合向量的加法运算,说一说,,之间的关系.
答案:(1)当,不共线时,由向量加法的三角形法则,根据三角形两边的和大于第三边,.
(2)当,共线时, ,方向相同,;,方向相反,(或),其中当向量的长度大于向量的长度时,,当向量的长度大于向量的长度时,.
综上,有.
问题5 我们知道,数的加法运算满足运算律,向量的加法,满足哪些运算律呢?
答案:作,,以AD,AB为邻边作,容易发现,,故.又,所以.
追问1:从前面已经知道,两个向量的和还是一个向量,因此我们可以用得到和向量与另外一个向量相加.而且我们也已经知道,如同数与数的加法一样,向量相加满足交换律,那么向量相加是否满足结合律呢?也就是说,三个向量相加时,最后的结果是否与求和的顺序有关呢?
答案:满足结合律.三个向量相加时,最后的结果是否与求和的顺序无关.因为向量的加法运算满足交换律和结合律,所以有限个向量相加的结果是唯一的,我们可以任意调换其中向量的位置,也可以任意决定相加的顺序.
设计意图:通过向量加法的交换律和结合律与实数加法的交换律和结合律形式上是完全心相同的,为以后线性运算做好铺垫.
追问2:给出如图中的三个向量,,,分别作出和,看看两个向量是否相等?
答案:
不难发现:,即向量的加法运算满足结合律.
设计意图:通过向量加法的交换律和结合律与实数加法的交换律和结合律形式上是完全心相同的,为以后线性运算做好铺垫.
追问3:图中向量的和,与向量相加的顺序有关吗?为什么?
答案:无关.原因在于向量的加法运算满足交换律,因此可以任意调整有关顺序.事实上,由于向量的加法满足交换律和结合律,所以有限个向量相加的结果是唯一的.
设计意图:利用作图,让学生观察和总结,在这个过程中,为了方便学生观察,可以增加相应的网格,以便学生平移有关向量.
例2 化简下列各式:(1) (2).
答案:
解:(1)
(2)
设计意图:注意其中用了向量加法的交换律和结合律.
例3 长江两岸之间没有大桥的地方,常常通过渡轮进行运输.如图,一艘船从长江南岸A地出发,垂直于对岸航行,航行速度的大小为15km/h,同时江水的速度为向东6km/h.
(1) 用向量表示江水速度、船速以及船实际航行的速度;
(2) 求船实际航行的速度的大小(结果保留小数点后一位)与方向(用与江水速度间的夹角表示,精确到1°).
答案:(1)如图,表示船速,表示江水速度,以AD,AB为邻边作,则表示船实际航行的速度.
(2) 在中,,,于是
.
因为,所以利用计算工具可得 .
因此,船实际航行速度的大小约为16.2km/h,方向与江水速度间的夹角约为68°.
【归纳小结】
问题7:(1)向量加法的三角形法则是什么?
(2)向量加法的平行四边形法则是什么?
答案:(1)一般地,平面上任意给定两个向量,,在该平面内任取一点A,作,作出向量,则向量称为向量,的和(也称为向量,的和向量).向量,的和向量记作,因此.
当,不共线时,求它们的和可用图1所示,当,共线时,求它们的和可用图2所示.因,正好能构成一个三角形,因此上述求两向量和的作图方法也常称为向量加法的三角形法则.
图1
图2
(2)当两个向量不共线时,可以通过作平行四边形的方法来得到它们的和:如图所示,平面上任意给定两个不共线的向量与,在该平面内任取一点A,作,,以AB,AC为邻边作一个平行四边形ABDC,作出向量,因为,因此.这种求两向量和的作图方法也常称为向量加法的平行四边形法则.
设计意图:通过梳理本节课的内容,能让学生更加明确向量的概念的有关知识.
教学内容
平面向量的加法运算,运算规则、几何意义和运算律.
教学目标
1.借助实例和平面向量的几何表示,掌握平面向量加法运算及运算规则,并理解其几何意义.
2.理解平面向量加法运算的运算律和运算性质.
(三)教学重点与难点
重点:向量加法运算的运算法则及其几何意义.
难点:对向量加法运算法则定义的理解.
(四)教学过程设计
【引入新课】
问题1:初中,我们学习过数的运算、代数式的运算,高中我们学习了集合的运算,平面向量,又有哪些运算呢?
答案:向量的运算包括向量的加法运算、向量的减法、数乘运算和向量的数量积运算.
设计意图:通过对这一单元内容的预习,让学生明晰本单元的学习目标,初步搭建平面向量学习内容的框架,对向量的运算有一个初步的认识.
【课堂探究】
问题2:如图所示,假设某人上午从点A到达了点B,下午从点B到达了点C.
(1)分别用向量表示出该人上午的位移、下午的位移以及这一天的位移;
(2)这一天的位移与上午的位移、下午的位移有什么联系?试从大小和方向两个角度加以阐述.
答案:(1)上午的位移是,下午的位移是,一天的位移是.(2)位移可以看成位移与的和.
设计意图:给出了向量加法的实际背景,这说明了研究向量加法的意义及合理性.这一内容的设置,旨在说明从生活中能抽象出数学问题,以此激发学生的学习热情.
引语:而本节课要讲的内容即为向量的加法.(板书:向量的加法)
已知两个非零向量,,在该平面内任取一点A,作,作出向量,则向量称为向量,的和(也称为向量,的和向量).向量,的和向量记作,因此(如图1).
求两个向量和的运算,叫做向量的加法.
因为正好能构成一个三角形,因此这种求两向量和的方法,称为向量加法的三角形法则.
图1
问题3 从物理学中我们已经知道,力既有大小也有方向,因此力是向量.
当在光滑的水平面上沿两个不同的方向拉动一个静止的物体时,如图所示,物体会沿着力或所在的方向运动吗?如果不会,物体的运动方向将是怎样的?
答案:合力在以OA,OB为邻边的平行四边形的对角线上,并且大小等于对角线的长.
设计意图:视学生的情况,引导学生联想到平抛物体时,物体运动速度的求法也遵循平行四边形法则.还可以引导学生举出更多实际生活中的例子,这样可以开阔学生的学习思路,提高学习兴趣.
我们知道,物理学中力的合成遵循平行四边形法则.因此,情境中的物体不会沿着或所在的方向运动,其会沿着以AB,AC为邻边的平行四边形的对角线运动.
追问1 从向量的角度进行分析,力和为起点相同的两个向量,你能得到求两个向量和的另一个法则吗
答案:以同一点O为起点的两个已知向量,,以OA,OB为邻边做,则以O为起点的向量(OC是的对角线)就是向量与的和.我们把这种做两个向量和的方法叫做向量加法的平行四边形法则.
追问2 向量加法的平行四边形法则与三角形法则一致吗?为什么?
答案:一致,如图由向量加法的三角形法则,.过点A做BC的平行线,过点C做AB的平行线,所做的两条直线相交于点D,四边形ABCD是平行四边形.由平行四边形的性质得AD=BC,所以.由向量加法的平行四边形法则也可得出,所以向量的三角形法则与平行四边形法则是一致的.
例1 如图,已知向量,,求做向量.
作法1:在平面内任取一点O,做,.则.
作法2: 在平面内任取一点O,做,.以OA,OB为邻边作,连接OC,则 .
问题4 当向量,共线时,是怎样的呢?
答案:(1)如果,中有一个向量为零向量,不妨设,则有,与实数加法类似;
(2)当,共线且,均不为零时,它们可以看作在数轴上的两个向量相加,其结果是一个向量,对应数轴上的一条有向线段,它们的和如下图所示.
两向量同向 两向量反向
追问1:向量,共线,它们的加法与数的加法有什么关系
答案:(1)与实数加法(即标量的加法)运算不同,实数加法是数值的运算,而向量的加法既要关注大小又要关注方向,两者有本质区别;
(2)由定义可知两个向量的和仍然是向量.除了需要通过作图来帮助学生理解两个向量的和之外,还需要带领学生分析的代数特点,要向学生说明:从左边往右边看,等式左边的两个向量,其中一个向量的终点与另外一个向量的始点是一样的,而右边的向量相当于消去了这个点;从右边往左边看,相当于是引入了个新的字母,而且引入的这个新字母是任意的.
(3)容易看出,当向量,共线时,以的终点做为的起点作出,就是连接的起点与的终点的向量(即首尾相接,再首尾相连) ,此时也符合向量加法的三角形法则.
追问2:结合向量的加法运算,说一说,,之间的关系.
答案:(1)当,不共线时,由向量加法的三角形法则,根据三角形两边的和大于第三边,.
(2)当,共线时, ,方向相同,;,方向相反,(或),其中当向量的长度大于向量的长度时,,当向量的长度大于向量的长度时,.
综上,有.
问题5 我们知道,数的加法运算满足运算律,向量的加法,满足哪些运算律呢?
答案:作,,以AD,AB为邻边作,容易发现,,故.又,所以.
追问1:从前面已经知道,两个向量的和还是一个向量,因此我们可以用得到和向量与另外一个向量相加.而且我们也已经知道,如同数与数的加法一样,向量相加满足交换律,那么向量相加是否满足结合律呢?也就是说,三个向量相加时,最后的结果是否与求和的顺序有关呢?
答案:满足结合律.三个向量相加时,最后的结果是否与求和的顺序无关.因为向量的加法运算满足交换律和结合律,所以有限个向量相加的结果是唯一的,我们可以任意调换其中向量的位置,也可以任意决定相加的顺序.
设计意图:通过向量加法的交换律和结合律与实数加法的交换律和结合律形式上是完全心相同的,为以后线性运算做好铺垫.
追问2:给出如图中的三个向量,,,分别作出和,看看两个向量是否相等?
答案:
不难发现:,即向量的加法运算满足结合律.
设计意图:通过向量加法的交换律和结合律与实数加法的交换律和结合律形式上是完全心相同的,为以后线性运算做好铺垫.
追问3:图中向量的和,与向量相加的顺序有关吗?为什么?
答案:无关.原因在于向量的加法运算满足交换律,因此可以任意调整有关顺序.事实上,由于向量的加法满足交换律和结合律,所以有限个向量相加的结果是唯一的.
设计意图:利用作图,让学生观察和总结,在这个过程中,为了方便学生观察,可以增加相应的网格,以便学生平移有关向量.
例2 化简下列各式:(1) (2).
答案:
解:(1)
(2)
设计意图:注意其中用了向量加法的交换律和结合律.
例3 长江两岸之间没有大桥的地方,常常通过渡轮进行运输.如图,一艘船从长江南岸A地出发,垂直于对岸航行,航行速度的大小为15km/h,同时江水的速度为向东6km/h.
(1) 用向量表示江水速度、船速以及船实际航行的速度;
(2) 求船实际航行的速度的大小(结果保留小数点后一位)与方向(用与江水速度间的夹角表示,精确到1°).
答案:(1)如图,表示船速,表示江水速度,以AD,AB为邻边作,则表示船实际航行的速度.
(2) 在中,,,于是
.
因为,所以利用计算工具可得 .
因此,船实际航行速度的大小约为16.2km/h,方向与江水速度间的夹角约为68°.
【归纳小结】
问题7:(1)向量加法的三角形法则是什么?
(2)向量加法的平行四边形法则是什么?
答案:(1)一般地,平面上任意给定两个向量,,在该平面内任取一点A,作,作出向量,则向量称为向量,的和(也称为向量,的和向量).向量,的和向量记作,因此.
当,不共线时,求它们的和可用图1所示,当,共线时,求它们的和可用图2所示.因,正好能构成一个三角形,因此上述求两向量和的作图方法也常称为向量加法的三角形法则.
图1
图2
(2)当两个向量不共线时,可以通过作平行四边形的方法来得到它们的和:如图所示,平面上任意给定两个不共线的向量与,在该平面内任取一点A,作,,以AB,AC为邻边作一个平行四边形ABDC,作出向量,因为,因此.这种求两向量和的作图方法也常称为向量加法的平行四边形法则.
设计意图:通过梳理本节课的内容,能让学生更加明确向量的概念的有关知识.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
