浙教版九年级上册期末测试数学基础卷(含解析)
文档属性
| 名称 | 浙教版九年级上册期末测试数学基础卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-28 21:00:52 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版九上期末测试基础卷(含解析)
一、单选题
1.抛物线 的顶点坐标是( ).
A. B. C. D.
2.如果,且是和的比例中项,那么等于( )
A. B. C. D.
3.从背面朝上的分别画有等腰三角形、平行四边形、矩形、圆的四张形状、大小相同的卡片中,随机抽取一张,则所抽得的图形既是中心对称图形又是轴对称图形的概率为( )
A. B. C. D.1
4.如图所示,在中,所对的圆周角,若为上一点,,则的度数为( ).
A. B. C. D.
5.将5张分别画有等边三角形、平行四边形、矩形、五角星、圆的卡片任意摆放,将有图形一面朝下,从中任意翻开一张,翻到中心对称图形的概率是( )
A. B. C. D.
6.若二次函数 的图象与 轴无交点,则 的取值范围为( )
A. B.
C. 且 D. 且
7.如图,AB是⊙O的直径,CD是⊙O的弦,∠ABD=59°,则∠C等于( )
A.29° B.31° C.59° D.62°
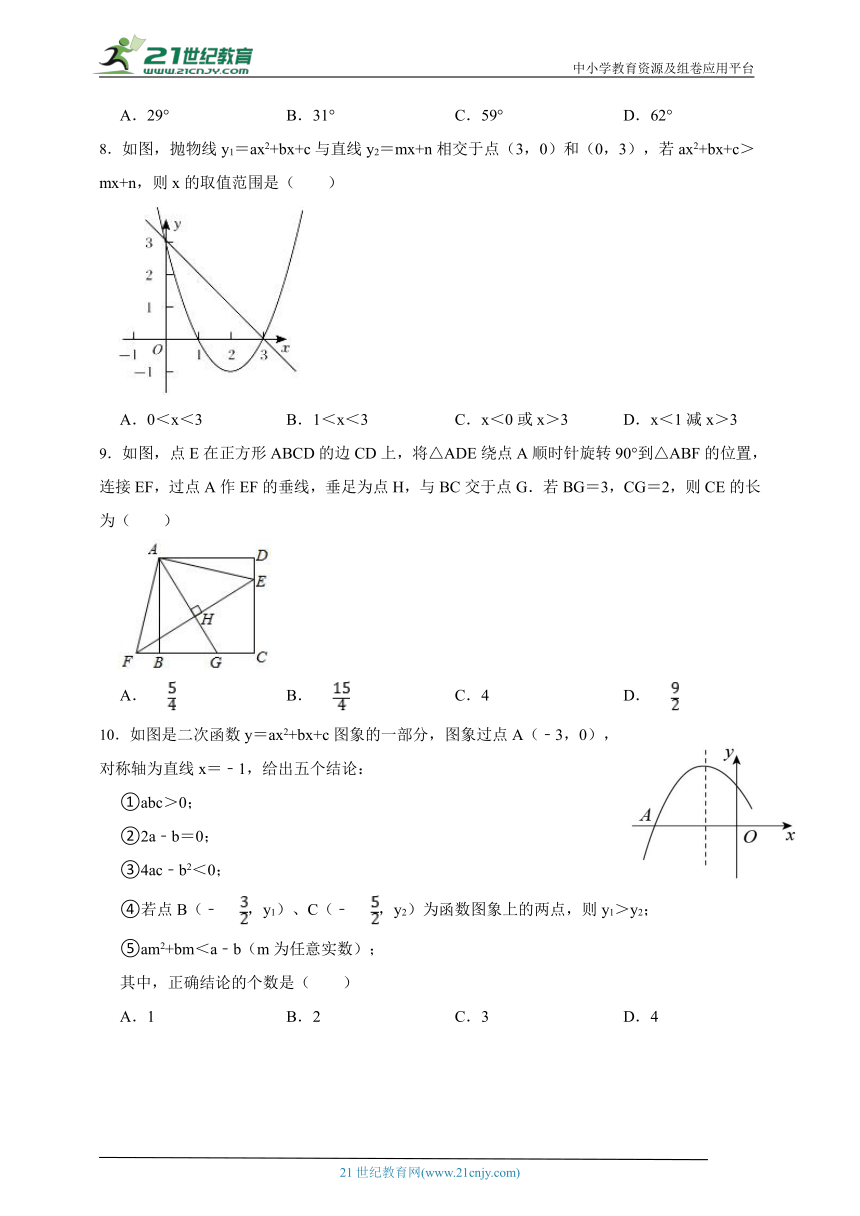
8.如图,抛物线y1=ax2+bx+c与直线y2=mx+n相交于点(3,0)和(0,3),若ax2+bx+c>mx+n,则x的取值范围是( )
A.0<x<3 B.1<x<3 C.x<0或x>3 D.x<1减x>3
9.如图,点E在正方形ABCD的边CD上,将△ADE绕点A顺时针旋转90°到△ABF的位置,连接EF,过点A作EF的垂线,垂足为点H,与BC交于点G.若BG=3,CG=2,则CE的长为( )
A. B. C.4 D.
10.如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出五个结论:
①abc>0;
②2a﹣b=0;
③4ac﹣b2<0;
④若点B(﹣,y1)、C(﹣,y2)为函数图象上的两点,则y1>y2;
⑤am2+bm<a﹣b(m为任意实数);
其中,正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题
11.二次函数y=(a-1)x2-x+a2-1 的图象经过原点,则a的值为 .
12.2022年冬奥会的主题口号是“一起向未来”,从5张上面分别写着“一”“起”“向”“未”“来”这5个字的卡片(大小,形状完全相同)中随机抽取一张,则这张卡片上面恰好写着“来”字的概率是 .
13.如图,用20 m长的铁丝网围成一个一面靠墙的矩形养殖场,其养殖场的最大面积 m2.
14.如图,在 中,D是 中点, ,若 的周长为6,则 的周长为 .
15.已知 ,点A (a,y1 ),B( a+1,y2)都在 二次函数 图像上,那么y1 、y2的大小关系是 .
16.三角形和三角形是一副直角三角板,按如图方式摆放,,,.
(1)若,则 ∠CAD 的度数为 ;
(2)若将三角形绕点A动,使得两个直角三角形的斜边平行,则的度数为 .
三、解答题
17.根据下列条件,求x:y的值.
(1)
(2)(x+y):y=4:5.
18.已知:△ABC在坐标平面内,三个顶点的坐标为A(0,3)、B(3,4)、C(2,2).(正方形网格中,每个小正方形边长为1个单位长度)
( 1 )画出△ABC向下平移4个单位得到的△A1B1C1;
( 2 )以B为位似中心,在网格中画出△A2BC2,使△A2BC2与△ABC位似,且位似比2:1,直接写出C2点坐标是 ;
( 3 )△A2BC2的面积是 平方单位.
19.如图,正方形ABCD中,AB=9,E是BC上一点,过E作EF⊥AE交CD于点F,连接AF.
(1)证明:ΔABE∽ΔECF.
(2)当BE=3时,求CF的长.
20.如图,以的一边为直径的半圆与其它两边的交点分别为.
(1)若,求证:.
(2)若为半圆的三等分点,且半径为2,图中阴影部分的面积是 .(结果保留和根号)
21.某校调查了若干名家长对“初中生带手机上学”现象的看法,统计整理并制作了如下的条形与扇形统计图,根据图中提供的信息,完成以下问题:
(1)本次共调查了 名家长;扇形统计图中“很赞同”所对应的圆心角是 度.已知该校共有1600名家长,则“不赞同”的家长约有 名;请补全条形统计图 ;
(2)从“不赞同”的五位家长中(两女三男),随机选取两位家长对全校家长进行“学生使用手机危害性”的专题讲座,请用树状图或列表法求出选中“1男1女”的概率.
22.如图,抛物线与轴交于原点与点,点为顶点.
(1)求抛物线的解析式;
(2)已知,将该抛物线向下平移个单位长度,若平移后的拋物线与线段只有一个公共点,直接写出的取值范围.
23.如图,在某场足球比赛中,球员甲从球门底部中心点O的正前方10 m处起脚射门,足球沿抛物线飞向球门中心线.当足球飞离地面高度为3 m时达到最高点,此时足球飞行的水平距离为6 m已知球门的横梁高为2.44 m.
(1)建立如图所示直角坐标系。此次射门,足球能否射进球门(不计其他影响因素)?
(2)守门员站在距离球门2 m处,他跳起时手的最大摸高为2.52 m.问:他能阻止球员甲的此次射门吗?如果不能,他至少后退多少米才能阻止球员甲的此次射门?
24.如图,在同一直角坐标系中,二次函数的图象与两坐标轴分别交于点A、点和点,且二次函数的对称轴直线,一次函数的图象与抛物线交于、两点.
(1)请求出点的坐标;
(2)请利用图象直接写出的大小.
(3)请利用图象直接写出当两函数的函数值的积小于0时的自变量取值范围.
答案解析部分
1.【答案】D
【解析】【解答】解:抛物线 的顶点坐标是(2,0),
故答案为:D.
【分析】根据抛物线的顶点式可以直接写出顶点坐标。
2.【答案】D
【解析】【解答】解:∵,b是a和c的比例中项,
即,
∴.
故答案为:D.
【分析】】根据比例中项的性质可得,再结合可得。
3.【答案】B
【解析】【解答】解: 分别画有等腰三角形、平行四边形、矩形、圆的四张形状、大小相同的卡片中,其中既是轴对称图形,又是中心对称图形的是:矩形,圆;
现从中任意抽取一张,则所抽得的图形既是中心对称图形又是轴对称图形的概率为 ,
故答案为:B.
【分析】 由四张形状、大小相同的卡片中分别画有等腰三角形、平行四边形、矩形、圆的四张形状、大小相同的卡片中,其中既是轴对称图形,又是中心对称图形的是:矩形,圆,然后利用概率公式计算即可.
4.【答案】B
【解析】【解答】解:∵弧AB=弧AB,
∴∠AOB=2∠ACB=100°,
∴∠BOP=∠AOB-∠AOP=45°.
故答案为:B.
【分析】根据同弧所对的圆心角等于圆周角的2倍可得∠AOB的度数,进而根据∠BOP=∠AOB-∠AOP即可算出答案.
5.【答案】C
【解析】【解答】解:∵将5张分别画有等边三角形、平行四边形、矩形、五角星、圆的卡片任意摆放,
∴共有5种等可能的结果,
∵中心对称图形的有平行四边形、矩形、圆,
∴从中任意翻开一张,翻到中心对称图形的概率是:.
故答案为:C.
【分析】利用概率公式求解即可。
6.【答案】B
【解析】【解答】 解: 是二次函数
则
令y=0,即
解得:
故答案为:B.
【分析】根据二次函数 的图象与x轴无交点, 得出,解不等式求出m的取值范围,即可得出答案.
7.【答案】B
【解析】【解答】∵AB是O的直径,
∴∠ADB=90°,
∵∠ABD=59°,
∴∠A=90° ∠ABD=31°,
∴∠C=∠A=31°
故答案为:B.
【分析】根据直径所对的圆周角是直角,可得∠ADB=90°,利用三角形内角和定理求出∠A的度数,利用同弧所对的圆周角相等即可求出∠C的度数.
8.【答案】C
【解析】【解答】解:根据函数图象,
当x<0或x>3时,y1>y2,
所以ax2+bx+c>mx+n的解集为x<0或x>3.
故答案为:C.
【分析】根据图象,找出抛物线在直线上方部分所对应的x的范围即可.
9.【答案】B
【解析】【解答】解:如图所示,连接EG,
由旋转可得,△ADE≌△ABF,
∴AE=AF,DE=BF,
又∵AG⊥EF,
∴H为EF的中点,
∴AG垂直平分EF,
∴EG=FG,
设CE=x,则DE=5 x=BF,FG=8 x,
∴EG=8 x,
∵∠C=90°,
∴Rt△CEG中,CE2+CG2=EG2,即x2+22=(8 x)2,
解得x=,
∴CE的长为,
故答案为:B.
【分析】连接EG,设CE=x,则DE=5 x=BF,FG=8 x,EG=8 x,利用勾股定理可得CE2+CG2=EG2,即x2+22=(8 x)2,最后求出x的值,即可得到CE的长。
10.【答案】D
【解析】【解答】解:∵抛物线开口向下,交y轴的正半轴,
∴a<0,c>0,
∵对称轴为直线x==-1,
∴b<0,2a=b,
∴abc>0,2a-b=0,故①②正确;
∵抛物线与x轴有两个交点,
∴>0,即 ,故③正确;
∴B(﹣,y1)距离对称轴较近,抛物线开口向下,
∴y1>y2,故④正确;
∵当x=-1时,y值最大,
∴am2+bm+c≤a﹣b+c,故⑤不正确;
综上,正确的结论是:①②③④共4个.
故答案为:D.
【分析】由图象可得:抛物线开口向下,交y轴的正半轴,对称轴为直线x==-1<0,据此可得a、b、c的正负,进而判断①②;根据抛物线与x轴有两个交点可判断③;根据距离对称轴越近的点,对应的函数值越大可判断④;当x=-1时,y值最大,据此判断⑤.
11.【答案】-1
【解析】【解答】解:∵二次函数y=(a-1)x2-x+a2-1 的图象经过原点,
∴a2-1=0,
∴a=±1,
∵a-1≠0,
∴a≠1,
∴a的值为-1.
故答案为:-1.
【分析】根据抛物线的图象与系数的关系,由抛物线的图象经过坐标原点得出其常数项应该等于0,且二次项的系数不为0,从而列出混合组,求解即可.
12.【答案】
【解析】【解答】从5张上面分别写着“一”“起”“向”“未”“来”这5个字的卡片(大小,形状完全相同)中随机抽取一张的结果可能有5种,其中恰好写着“来”字的结果有1种,
∴随机抽取的这张卡片恰好写着“来”字的概率 .
故答案为: .
【分析】利用概率公式求解即可。
13.【答案】50
【解析】【解答】设与墙平行的一边长为xm,则另一面为 ,
其面积=,
∴最大面积为 ;
即最大面积是50m2.
故答案是50.
【分析】设与墙平行的一边长为xm,则另一面为 ,根据题意列出函数解析式其面积=,再利用二次函数的性质求解即可。
14.【答案】12
【解析】【解答】解:∵ ,
∴ ,
又∵D是 中点,
∴ ,即 与 的相似比为1:2,
∴ 与 的周长比为1:2,
∵ 的周长为6,
∴ 的周长为12,
故答案为:12.
【分析】由 ,可知 ,再由D是 中点,可得到相似比,即可求出 的周长.
15.【答案】y1>y2
【解析】【解答】解:抛物线的对称轴为直线 ,
∵a<-3,点A (a,y1 ),B( a+1,y2)
∴点A和点B都在对称轴的左侧,y的值随着x的值增大而减小,而a<a+1,∴y1>y2.
故答案为y1>y2.
【分析】根据二次函数 的性质,在对称轴的左侧,y随x增大而减小,即可求解.
16.【答案】(1)
(2)或
【解析】【解答】解:(1)如图,AD与BC相交于点F,
∵BC⊥AD,
∴∠AFC=90°,
又∵∠C=30°,
∴∠CAD=180°-∠C-∠AFC=180°-30°-90°=60°。
故答案为:60°,
(2)分为以下两种情况:
①如图1,
过点A作AF∥BC,
∵DE∥BC,
∴AF∥DE,
∴BC∥AF∥DE,
∴∠CAF=∠C=30°,∠DAF=∠D=45°,
∴∠DAC=∠CAF+∠DAF=30°+45°=75°;
②如图2,
延长CB交AD于点F,
∵DE∥BC,
∴∠AFC=∠D=45°,
∴∠BAD=∠ABC-∠AFC=60°-45°=15°,
∴DAC=∠BAD+∠BAC=15°+90°=105°。
故答案为:105°或75°。
【分析】(1)首先根据BC⊥AD,得到∠AFC=90°,然后在△ACF中,由三角形的内角和,求得∠CAD的度数;
(2)分成两种情况:根据平行线的性质,分别求得∠DAC的度数即可。
17.【答案】(1)解:∵
∴3y=4x,即x:y=.
(2)解:∵ (x+y):y=4:5,
∴5(x+y)=4y,
∴5x=-y,即x:y=.
【解析】【分析】根据比例的性质将等式变形,继而求解.
18.【答案】解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:C2(1,0)
(3)10
【解析】【解答】解:(2)如图所示:△A2BC2即为所求,C2点坐标为(1,0),
故答案为:(1,0);
(3)∵A2C2=BC2=,A2B=,
∴A2C22+BC22= A2B2,
∴△A2BC2是等腰直角三角形,且∠A2C2B=90°,
∴△A2BC2的面积位为:×()2=10平方单位,
故答案为:10.
【分析】(1)根据题意并结合网格图的特征可求解;
(2)根据位似比并结合网格图的特征可求解;
(3)根据网格图的特征用勾股定理求得A2C2=BC2、A2B的值,然后根据勾股定理的逆定理可判断△A2BC2是等腰直角三角形,于是根据S△=BC22可求解.
19.【答案】(1)证明:∵四边形是正方形
∴
∴
∵
∴
∴
∴
(2)∵,
∴,
∴,
∴
20.【答案】(1)证明:是直径,∴,
∴,∵,
∴,
∵,
∴,
∴;
(2)
【解析】【解答】(2)连接OE,如图所示:
∵D、E为半圆的三等分点,
∴∠BOE=×180°=60°,
∵OE=OB,
∴△OEB是等边三角形,
∴∠EOB=60°,
∵OE=2,
∴S△OEB=S扇形OBE-S△OEB=,
故答案为:.
【分析】(1)先利用“ASA”证出,再利用全等三角形的性质可得;
(2)利用扇形面积公式及割补法求出阴影部分的面积即可.
21.【答案】(1)200;36;720;
(2)解:用列表法表示所有可能出现的情况如下:
共有20种可能出现的情况,符合题意“1男1女”的有12种,
∴P(1男1女)= ,
答:选中“1男1女”的概率为 .
【解析】【解答】解:(1)总人数:50÷25%=200名,无所谓人数:200×20%=40名,很赞同人数:200﹣90﹣50﹣40=20名,
很赞同对应圆心角:360°× =36°,
1600× =720名,
故答案为:200,36,720,补全条形统计图如图所示:
【分析】(1)从两个统计图可得,“赞同”的有50名,占调查总人数的25%,可求出调查总人数;进而求出“无所谓”和“很赞同”的人数,很赞同的圆心角度数为360°的 ,样本估计总体,样本中“不赞同”的占 ,估计总体1600户的 是“不赞同”的人数;即可补全条形统计图:(2)用列表法或树状图法列举出所有等可能出现的情况,从中找出1男1女的情况数,进而求出概率.
22.【答案】(1)解:抛物线的解析式为
(2)解:的取值范围是
【解析】【解答】(1)将点O(0,0)代入,
可得:,
解得:,
∴抛物线的解析式为:,
故答案为:;
(2)根据(1)中的函数解析式可得点B的坐标为(2,-2),
当k=0时,抛物线与线段BQ有一个公共点为点B,
将x=-1代入抛物线的函数解析式得:,
∵,
∴将抛物线向下平移2个单位长度时,抛物线与线段BQ的公共点为点Q,
若再向下平移,则线段BQ与抛物线没有公共点,
∴k的取值范围是,
故答案为:.
【分析】(1)将点(0,0)代入解析式求出a的值即可;
(2)根据“ 平移后的拋物线与线段只有一个公共点 ”列出算式求解即可.
23.【答案】(1)解:由题图可知:抛物线的顶点坐标为(4,3),与x轴的交点坐标为(10,0),
故设抛物线的解析式为:y=a(x-4)2+3,
将(10,0)代入抛物线的解析式中得,
0=a(10-4)2+3,
解得:a=,
所以抛物线的解析式为:y=(x-4)2+3,
当x=0时,y=(0-4)2+3=<2.44,
所以足球能射进球门;
(2)解:当x=2时,y=(2-4)2+3=>2.52,
所以守门员不能阻止此次射门;
由(x-4)2+3=2.52得,
x1=1.6,x2=6.4(舍去),
则2-1.6=0.4(米),
答:他至少后退0.4米才能阻止球员甲的此次射门.
【解析】【分析】(1)由题图可知:抛物线的顶点坐标为(4,3),与x轴的交点坐标为(10,0),故利用待定系数法求抛物线的解析式得时候,设成顶点式计算更简单,然后将x=0代入所求的抛物线的解析式算出对应的函数值,将该值与球门的横梁高为2.44m比大小,即可判断得出答案;
(2)将x=2代入所求的抛物线的解析式算出对应的函数值,将该值与守门员跳起时手的最大摸高2.52m比大小,即可判断能否阻止球员甲的此次射门;进而将y=2.52代入(1)所求的抛物线的解析式算出对应的自变量的值,用2m减去该值即可得出答案.
24.【答案】(1)∵一次函数的图象与两坐标轴分別交于点、点,且二次函数的刏称轴直线,
;
(2)由图象可知,当或时,.
(3)由图象可知,两函数的函数俏的积小于0时的白变星取俏范围足.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙教版九上期末测试基础卷(含解析)
一、单选题
1.抛物线 的顶点坐标是( ).
A. B. C. D.
2.如果,且是和的比例中项,那么等于( )
A. B. C. D.
3.从背面朝上的分别画有等腰三角形、平行四边形、矩形、圆的四张形状、大小相同的卡片中,随机抽取一张,则所抽得的图形既是中心对称图形又是轴对称图形的概率为( )
A. B. C. D.1
4.如图所示,在中,所对的圆周角,若为上一点,,则的度数为( ).
A. B. C. D.
5.将5张分别画有等边三角形、平行四边形、矩形、五角星、圆的卡片任意摆放,将有图形一面朝下,从中任意翻开一张,翻到中心对称图形的概率是( )
A. B. C. D.
6.若二次函数 的图象与 轴无交点,则 的取值范围为( )
A. B.
C. 且 D. 且
7.如图,AB是⊙O的直径,CD是⊙O的弦,∠ABD=59°,则∠C等于( )
A.29° B.31° C.59° D.62°
8.如图,抛物线y1=ax2+bx+c与直线y2=mx+n相交于点(3,0)和(0,3),若ax2+bx+c>mx+n,则x的取值范围是( )
A.0<x<3 B.1<x<3 C.x<0或x>3 D.x<1减x>3
9.如图,点E在正方形ABCD的边CD上,将△ADE绕点A顺时针旋转90°到△ABF的位置,连接EF,过点A作EF的垂线,垂足为点H,与BC交于点G.若BG=3,CG=2,则CE的长为( )
A. B. C.4 D.
10.如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出五个结论:
①abc>0;
②2a﹣b=0;
③4ac﹣b2<0;
④若点B(﹣,y1)、C(﹣,y2)为函数图象上的两点,则y1>y2;
⑤am2+bm<a﹣b(m为任意实数);
其中,正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题
11.二次函数y=(a-1)x2-x+a2-1 的图象经过原点,则a的值为 .
12.2022年冬奥会的主题口号是“一起向未来”,从5张上面分别写着“一”“起”“向”“未”“来”这5个字的卡片(大小,形状完全相同)中随机抽取一张,则这张卡片上面恰好写着“来”字的概率是 .
13.如图,用20 m长的铁丝网围成一个一面靠墙的矩形养殖场,其养殖场的最大面积 m2.
14.如图,在 中,D是 中点, ,若 的周长为6,则 的周长为 .
15.已知 ,点A (a,y1 ),B( a+1,y2)都在 二次函数 图像上,那么y1 、y2的大小关系是 .
16.三角形和三角形是一副直角三角板,按如图方式摆放,,,.
(1)若,则 ∠CAD 的度数为 ;
(2)若将三角形绕点A动,使得两个直角三角形的斜边平行,则的度数为 .
三、解答题
17.根据下列条件,求x:y的值.
(1)
(2)(x+y):y=4:5.
18.已知:△ABC在坐标平面内,三个顶点的坐标为A(0,3)、B(3,4)、C(2,2).(正方形网格中,每个小正方形边长为1个单位长度)
( 1 )画出△ABC向下平移4个单位得到的△A1B1C1;
( 2 )以B为位似中心,在网格中画出△A2BC2,使△A2BC2与△ABC位似,且位似比2:1,直接写出C2点坐标是 ;
( 3 )△A2BC2的面积是 平方单位.
19.如图,正方形ABCD中,AB=9,E是BC上一点,过E作EF⊥AE交CD于点F,连接AF.
(1)证明:ΔABE∽ΔECF.
(2)当BE=3时,求CF的长.
20.如图,以的一边为直径的半圆与其它两边的交点分别为.
(1)若,求证:.
(2)若为半圆的三等分点,且半径为2,图中阴影部分的面积是 .(结果保留和根号)
21.某校调查了若干名家长对“初中生带手机上学”现象的看法,统计整理并制作了如下的条形与扇形统计图,根据图中提供的信息,完成以下问题:
(1)本次共调查了 名家长;扇形统计图中“很赞同”所对应的圆心角是 度.已知该校共有1600名家长,则“不赞同”的家长约有 名;请补全条形统计图 ;
(2)从“不赞同”的五位家长中(两女三男),随机选取两位家长对全校家长进行“学生使用手机危害性”的专题讲座,请用树状图或列表法求出选中“1男1女”的概率.
22.如图,抛物线与轴交于原点与点,点为顶点.
(1)求抛物线的解析式;
(2)已知,将该抛物线向下平移个单位长度,若平移后的拋物线与线段只有一个公共点,直接写出的取值范围.
23.如图,在某场足球比赛中,球员甲从球门底部中心点O的正前方10 m处起脚射门,足球沿抛物线飞向球门中心线.当足球飞离地面高度为3 m时达到最高点,此时足球飞行的水平距离为6 m已知球门的横梁高为2.44 m.
(1)建立如图所示直角坐标系。此次射门,足球能否射进球门(不计其他影响因素)?
(2)守门员站在距离球门2 m处,他跳起时手的最大摸高为2.52 m.问:他能阻止球员甲的此次射门吗?如果不能,他至少后退多少米才能阻止球员甲的此次射门?
24.如图,在同一直角坐标系中,二次函数的图象与两坐标轴分别交于点A、点和点,且二次函数的对称轴直线,一次函数的图象与抛物线交于、两点.
(1)请求出点的坐标;
(2)请利用图象直接写出的大小.
(3)请利用图象直接写出当两函数的函数值的积小于0时的自变量取值范围.
答案解析部分
1.【答案】D
【解析】【解答】解:抛物线 的顶点坐标是(2,0),
故答案为:D.
【分析】根据抛物线的顶点式可以直接写出顶点坐标。
2.【答案】D
【解析】【解答】解:∵,b是a和c的比例中项,
即,
∴.
故答案为:D.
【分析】】根据比例中项的性质可得,再结合可得。
3.【答案】B
【解析】【解答】解: 分别画有等腰三角形、平行四边形、矩形、圆的四张形状、大小相同的卡片中,其中既是轴对称图形,又是中心对称图形的是:矩形,圆;
现从中任意抽取一张,则所抽得的图形既是中心对称图形又是轴对称图形的概率为 ,
故答案为:B.
【分析】 由四张形状、大小相同的卡片中分别画有等腰三角形、平行四边形、矩形、圆的四张形状、大小相同的卡片中,其中既是轴对称图形,又是中心对称图形的是:矩形,圆,然后利用概率公式计算即可.
4.【答案】B
【解析】【解答】解:∵弧AB=弧AB,
∴∠AOB=2∠ACB=100°,
∴∠BOP=∠AOB-∠AOP=45°.
故答案为:B.
【分析】根据同弧所对的圆心角等于圆周角的2倍可得∠AOB的度数,进而根据∠BOP=∠AOB-∠AOP即可算出答案.
5.【答案】C
【解析】【解答】解:∵将5张分别画有等边三角形、平行四边形、矩形、五角星、圆的卡片任意摆放,
∴共有5种等可能的结果,
∵中心对称图形的有平行四边形、矩形、圆,
∴从中任意翻开一张,翻到中心对称图形的概率是:.
故答案为:C.
【分析】利用概率公式求解即可。
6.【答案】B
【解析】【解答】 解: 是二次函数
则
令y=0,即
解得:
故答案为:B.
【分析】根据二次函数 的图象与x轴无交点, 得出,解不等式求出m的取值范围,即可得出答案.
7.【答案】B
【解析】【解答】∵AB是O的直径,
∴∠ADB=90°,
∵∠ABD=59°,
∴∠A=90° ∠ABD=31°,
∴∠C=∠A=31°
故答案为:B.
【分析】根据直径所对的圆周角是直角,可得∠ADB=90°,利用三角形内角和定理求出∠A的度数,利用同弧所对的圆周角相等即可求出∠C的度数.
8.【答案】C
【解析】【解答】解:根据函数图象,
当x<0或x>3时,y1>y2,
所以ax2+bx+c>mx+n的解集为x<0或x>3.
故答案为:C.
【分析】根据图象,找出抛物线在直线上方部分所对应的x的范围即可.
9.【答案】B
【解析】【解答】解:如图所示,连接EG,
由旋转可得,△ADE≌△ABF,
∴AE=AF,DE=BF,
又∵AG⊥EF,
∴H为EF的中点,
∴AG垂直平分EF,
∴EG=FG,
设CE=x,则DE=5 x=BF,FG=8 x,
∴EG=8 x,
∵∠C=90°,
∴Rt△CEG中,CE2+CG2=EG2,即x2+22=(8 x)2,
解得x=,
∴CE的长为,
故答案为:B.
【分析】连接EG,设CE=x,则DE=5 x=BF,FG=8 x,EG=8 x,利用勾股定理可得CE2+CG2=EG2,即x2+22=(8 x)2,最后求出x的值,即可得到CE的长。
10.【答案】D
【解析】【解答】解:∵抛物线开口向下,交y轴的正半轴,
∴a<0,c>0,
∵对称轴为直线x==-1,
∴b<0,2a=b,
∴abc>0,2a-b=0,故①②正确;
∵抛物线与x轴有两个交点,
∴>0,即 ,故③正确;
∴B(﹣,y1)距离对称轴较近,抛物线开口向下,
∴y1>y2,故④正确;
∵当x=-1时,y值最大,
∴am2+bm+c≤a﹣b+c,故⑤不正确;
综上,正确的结论是:①②③④共4个.
故答案为:D.
【分析】由图象可得:抛物线开口向下,交y轴的正半轴,对称轴为直线x==-1<0,据此可得a、b、c的正负,进而判断①②;根据抛物线与x轴有两个交点可判断③;根据距离对称轴越近的点,对应的函数值越大可判断④;当x=-1时,y值最大,据此判断⑤.
11.【答案】-1
【解析】【解答】解:∵二次函数y=(a-1)x2-x+a2-1 的图象经过原点,
∴a2-1=0,
∴a=±1,
∵a-1≠0,
∴a≠1,
∴a的值为-1.
故答案为:-1.
【分析】根据抛物线的图象与系数的关系,由抛物线的图象经过坐标原点得出其常数项应该等于0,且二次项的系数不为0,从而列出混合组,求解即可.
12.【答案】
【解析】【解答】从5张上面分别写着“一”“起”“向”“未”“来”这5个字的卡片(大小,形状完全相同)中随机抽取一张的结果可能有5种,其中恰好写着“来”字的结果有1种,
∴随机抽取的这张卡片恰好写着“来”字的概率 .
故答案为: .
【分析】利用概率公式求解即可。
13.【答案】50
【解析】【解答】设与墙平行的一边长为xm,则另一面为 ,
其面积=,
∴最大面积为 ;
即最大面积是50m2.
故答案是50.
【分析】设与墙平行的一边长为xm,则另一面为 ,根据题意列出函数解析式其面积=,再利用二次函数的性质求解即可。
14.【答案】12
【解析】【解答】解:∵ ,
∴ ,
又∵D是 中点,
∴ ,即 与 的相似比为1:2,
∴ 与 的周长比为1:2,
∵ 的周长为6,
∴ 的周长为12,
故答案为:12.
【分析】由 ,可知 ,再由D是 中点,可得到相似比,即可求出 的周长.
15.【答案】y1>y2
【解析】【解答】解:抛物线的对称轴为直线 ,
∵a<-3,点A (a,y1 ),B( a+1,y2)
∴点A和点B都在对称轴的左侧,y的值随着x的值增大而减小,而a<a+1,∴y1>y2.
故答案为y1>y2.
【分析】根据二次函数 的性质,在对称轴的左侧,y随x增大而减小,即可求解.
16.【答案】(1)
(2)或
【解析】【解答】解:(1)如图,AD与BC相交于点F,
∵BC⊥AD,
∴∠AFC=90°,
又∵∠C=30°,
∴∠CAD=180°-∠C-∠AFC=180°-30°-90°=60°。
故答案为:60°,
(2)分为以下两种情况:
①如图1,
过点A作AF∥BC,
∵DE∥BC,
∴AF∥DE,
∴BC∥AF∥DE,
∴∠CAF=∠C=30°,∠DAF=∠D=45°,
∴∠DAC=∠CAF+∠DAF=30°+45°=75°;
②如图2,
延长CB交AD于点F,
∵DE∥BC,
∴∠AFC=∠D=45°,
∴∠BAD=∠ABC-∠AFC=60°-45°=15°,
∴DAC=∠BAD+∠BAC=15°+90°=105°。
故答案为:105°或75°。
【分析】(1)首先根据BC⊥AD,得到∠AFC=90°,然后在△ACF中,由三角形的内角和,求得∠CAD的度数;
(2)分成两种情况:根据平行线的性质,分别求得∠DAC的度数即可。
17.【答案】(1)解:∵
∴3y=4x,即x:y=.
(2)解:∵ (x+y):y=4:5,
∴5(x+y)=4y,
∴5x=-y,即x:y=.
【解析】【分析】根据比例的性质将等式变形,继而求解.
18.【答案】解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:C2(1,0)
(3)10
【解析】【解答】解:(2)如图所示:△A2BC2即为所求,C2点坐标为(1,0),
故答案为:(1,0);
(3)∵A2C2=BC2=,A2B=,
∴A2C22+BC22= A2B2,
∴△A2BC2是等腰直角三角形,且∠A2C2B=90°,
∴△A2BC2的面积位为:×()2=10平方单位,
故答案为:10.
【分析】(1)根据题意并结合网格图的特征可求解;
(2)根据位似比并结合网格图的特征可求解;
(3)根据网格图的特征用勾股定理求得A2C2=BC2、A2B的值,然后根据勾股定理的逆定理可判断△A2BC2是等腰直角三角形,于是根据S△=BC22可求解.
19.【答案】(1)证明:∵四边形是正方形
∴
∴
∵
∴
∴
∴
(2)∵,
∴,
∴,
∴
20.【答案】(1)证明:是直径,∴,
∴,∵,
∴,
∵,
∴,
∴;
(2)
【解析】【解答】(2)连接OE,如图所示:
∵D、E为半圆的三等分点,
∴∠BOE=×180°=60°,
∵OE=OB,
∴△OEB是等边三角形,
∴∠EOB=60°,
∵OE=2,
∴S△OEB=S扇形OBE-S△OEB=,
故答案为:.
【分析】(1)先利用“ASA”证出,再利用全等三角形的性质可得;
(2)利用扇形面积公式及割补法求出阴影部分的面积即可.
21.【答案】(1)200;36;720;
(2)解:用列表法表示所有可能出现的情况如下:
共有20种可能出现的情况,符合题意“1男1女”的有12种,
∴P(1男1女)= ,
答:选中“1男1女”的概率为 .
【解析】【解答】解:(1)总人数:50÷25%=200名,无所谓人数:200×20%=40名,很赞同人数:200﹣90﹣50﹣40=20名,
很赞同对应圆心角:360°× =36°,
1600× =720名,
故答案为:200,36,720,补全条形统计图如图所示:
【分析】(1)从两个统计图可得,“赞同”的有50名,占调查总人数的25%,可求出调查总人数;进而求出“无所谓”和“很赞同”的人数,很赞同的圆心角度数为360°的 ,样本估计总体,样本中“不赞同”的占 ,估计总体1600户的 是“不赞同”的人数;即可补全条形统计图:(2)用列表法或树状图法列举出所有等可能出现的情况,从中找出1男1女的情况数,进而求出概率.
22.【答案】(1)解:抛物线的解析式为
(2)解:的取值范围是
【解析】【解答】(1)将点O(0,0)代入,
可得:,
解得:,
∴抛物线的解析式为:,
故答案为:;
(2)根据(1)中的函数解析式可得点B的坐标为(2,-2),
当k=0时,抛物线与线段BQ有一个公共点为点B,
将x=-1代入抛物线的函数解析式得:,
∵,
∴将抛物线向下平移2个单位长度时,抛物线与线段BQ的公共点为点Q,
若再向下平移,则线段BQ与抛物线没有公共点,
∴k的取值范围是,
故答案为:.
【分析】(1)将点(0,0)代入解析式求出a的值即可;
(2)根据“ 平移后的拋物线与线段只有一个公共点 ”列出算式求解即可.
23.【答案】(1)解:由题图可知:抛物线的顶点坐标为(4,3),与x轴的交点坐标为(10,0),
故设抛物线的解析式为:y=a(x-4)2+3,
将(10,0)代入抛物线的解析式中得,
0=a(10-4)2+3,
解得:a=,
所以抛物线的解析式为:y=(x-4)2+3,
当x=0时,y=(0-4)2+3=<2.44,
所以足球能射进球门;
(2)解:当x=2时,y=(2-4)2+3=>2.52,
所以守门员不能阻止此次射门;
由(x-4)2+3=2.52得,
x1=1.6,x2=6.4(舍去),
则2-1.6=0.4(米),
答:他至少后退0.4米才能阻止球员甲的此次射门.
【解析】【分析】(1)由题图可知:抛物线的顶点坐标为(4,3),与x轴的交点坐标为(10,0),故利用待定系数法求抛物线的解析式得时候,设成顶点式计算更简单,然后将x=0代入所求的抛物线的解析式算出对应的函数值,将该值与球门的横梁高为2.44m比大小,即可判断得出答案;
(2)将x=2代入所求的抛物线的解析式算出对应的函数值,将该值与守门员跳起时手的最大摸高2.52m比大小,即可判断能否阻止球员甲的此次射门;进而将y=2.52代入(1)所求的抛物线的解析式算出对应的自变量的值,用2m减去该值即可得出答案.
24.【答案】(1)∵一次函数的图象与两坐标轴分別交于点、点,且二次函数的刏称轴直线,
;
(2)由图象可知,当或时,.
(3)由图象可知,两函数的函数俏的积小于0时的白变星取俏范围足.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
