四川省成都市锦江区嘉祥外国语学校2022-2023学年八年级(下)开学数学试卷(含答案)
文档属性
| 名称 | 四川省成都市锦江区嘉祥外国语学校2022-2023学年八年级(下)开学数学试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 317.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-29 08:52:56 | ||
图片预览


文档简介
2022-2023学年四川省成都市锦江区嘉祥外国语学校八年级(下)开学数学试卷
一、选择题(共8小题,满分32分,每小题4分)
1.(4分)下列计算正确的是( )
A. B. C. D.
2.(4分)某中学演讲比赛中,进入决赛的七位选手的成绩分别为91、93、95、96、97、97、97,那么这组数据的众数和中位数分别是( )
A.93,96 B.97,97 C.97,96 D.93,97
3.(4分)下列各组数中不能作为直角三角形的三边长的是( )
A.6、8、10 B.9、12、15 C.7、24、25 D.、、
4.(4分)若点P(m﹣1,5)与点Q(3,2﹣n)关于x轴对称,则m+n的值是( )
A.1 B.3 C.5 D.11
5.(4分)将一副直角三角板(∠A=∠FDE=90°,∠F=45°,∠C=60°,点D在边AB上)按图中所示位置摆放,两条斜边为EF,BC,且EF∥BC,则∠ADF等于
( )
A.70° B.75° C.80° D.85°
6.(4分)育才中学初一年级某班为奖励在校运动会上取得好成绩的同学,花了184元购买甲、乙两种奖品共20件.其中甲种奖品每件8元,乙种奖品每件6元,若设购买甲种奖品x件,乙种奖品y件,则所列方程组正确的是( )
A. B.
C. D.
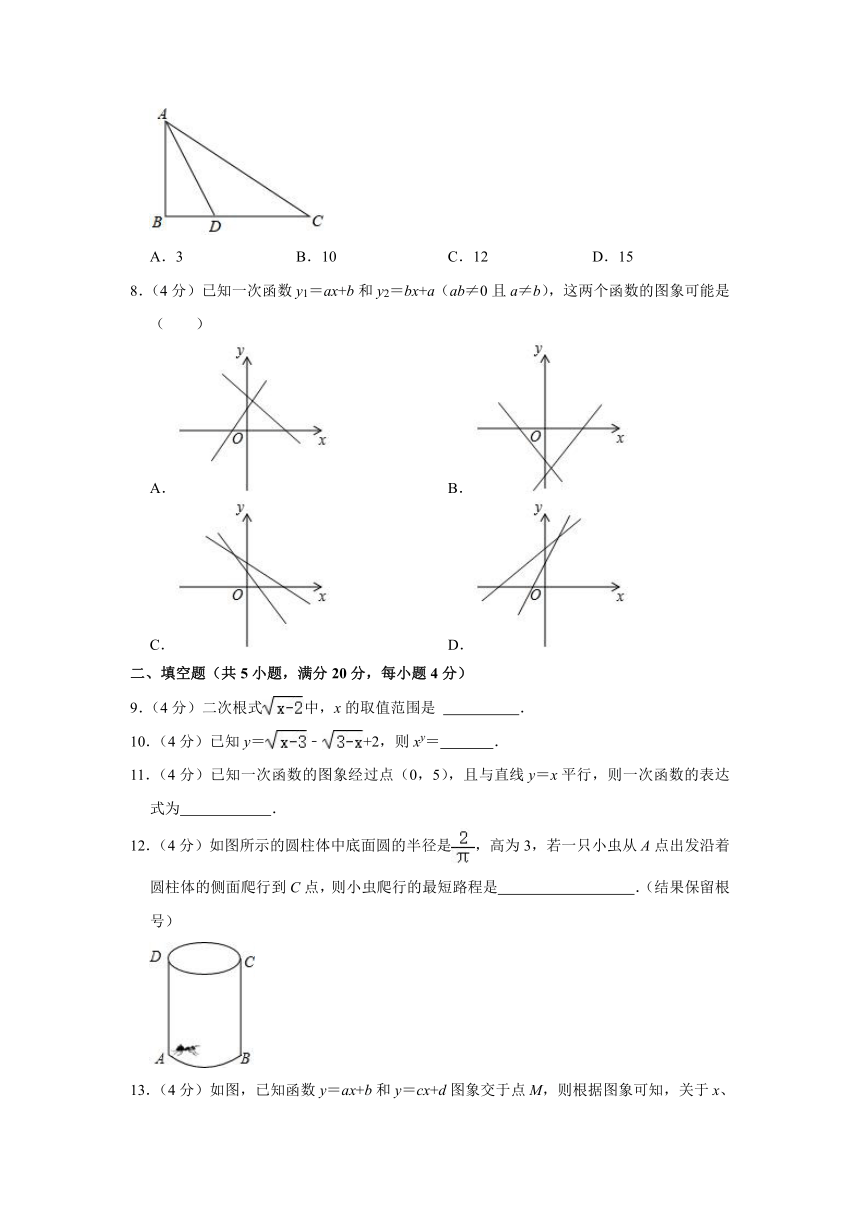
7.(4分)如图,在△ABC中,∠B=90°,AB=6,BC=8,AD为∠BAC的角平分线,则三角形ADC的面积为( )
A.3 B.10 C.12 D.15
8.(4分)已知一次函数y1=ax+b和y2=bx+a(ab≠0且a≠b),这两个函数的图象可能是( )
A. B.
C. D.
二、填空题(共5小题,满分20分,每小题4分)
9.(4分)二次根式中,x的取值范围是 .
10.(4分)已知y=﹣+2,则xy= .
11.(4分)已知一次函数的图象经过点(0,5),且与直线y=x平行,则一次函数的表达式为 .
12.(4分)如图所示的圆柱体中底面圆的半径是,高为3,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是 .(结果保留根号)
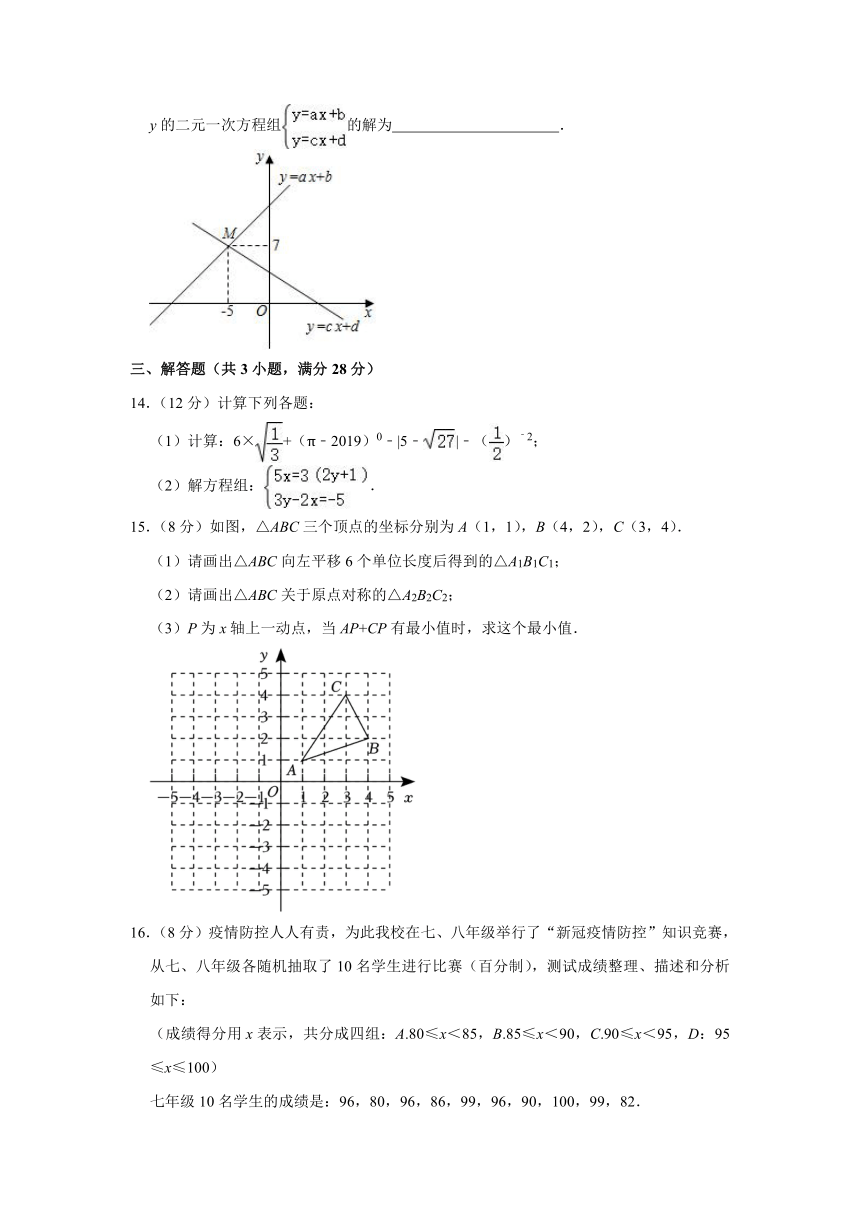
13.(4分)如图,已知函数y=ax+b和y=cx+d图象交于点M,则根据图象可知,关于x、y的二元一次方程组的解为 .
三、解答题(共3小题,满分28分)
14.(12分)计算下列各题:
(1)计算:6×+(π﹣2019)0﹣|5﹣|﹣()﹣2;
(2)解方程组:.
15.(8分)如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;
(3)P为x轴上一动点,当AP+CP有最小值时,求这个最小值.
16.(8分)疫情防控人人有责,为此我校在七、八年级举行了“新冠疫情防控”知识竞赛,从七、八年级各随机抽取了10名学生进行比赛(百分制),测试成绩整理、描述和分析如下:
(成绩得分用x表示,共分成四组:A.80≤x<85,B.85≤x<90,C.90≤x<95,D:95≤x≤100)
七年级10名学生的成绩是:96,80,96,86,99,96,90,100,99,82.
八年级10名学生的成绩在C组中的数据是:94,90,92.
七、八年级抽取的学生竞赛成绩统计表
年级 平均数 中位数 众数 方差
七年级 92.4 b c 52
八年级 92 93 100 50.4
根据以上信息,解答下列问题:
(1)这次比赛中 年级成绩更平衡,更稳定;
(2)直接写出上述a、b、c的值:a= ,b= ,c= ;
(3)我校八年级共1200人参加了此次调查活动,估计参加此次调查活动成绩优秀(x≥90)的八年级学生人数是多少?
17.(10分)如图,将长方形ABCD沿对角线AC翻折,点B落在点E处,EC交AD于点F.
(1)求证:△AEF≌△CDF;
(2)若AB=4,BC=8,求DF的长.
18.(10分)已知平面直角坐标系中,直线AB图象上有两点 和点B(5,),与x轴交于点C,与y轴交于点D.
(1)求直线AB的表达式;
(2)若在y轴上有一异于原点的点P,使△PAB为等腰三角形,求点P的坐标;
(3)若将线段AB沿直线y=mx+n(m≠0)进行对折得到线段A1B1,且点A1始终在直线OA上,当线段A1B1与x轴有交点时,求n的取值的最大值.
四、填空题(共5小题,满分20分,每小题4分)
19.(4分)已知x=+2,y=﹣2,则x2+y2+2xy= .
20.(4分)如图,在平面直角坐标系中,点A,B的坐标分别为(1,1),(1,4),直线y=2x+b与线段AB有公共点,则b的取值范围是 .
21.(4分)对于实数a,b,定义运算“◆”:a◆b=,例如3◆2,因为3>2,所以3◆2==,若x,y满足方程组,则(x◆y)◆x= .
22.(4分)在等腰直角三角形ABC中,∠ACB=90°,CD⊥AB于点D,点E是平面内任意一点,连接DE,如图1,当点E在边BC上时,过点D作DF⊥DE交AC于点F.
(1)线段AF,DE,BE之间满足的数量关系是 .
(2)如图2,当点E在△BDC内部时,连接AE,CE,若DB=5,DE=3,∠AED=45°,求线段CE的长为 .
23.(4分)定义:点P与图形W上各点连接的所有线段中,若线段PA最短,则线段PA的长度称为点P到图形W的距离,记为d(P,图形W).例如,在图1中,原点O(0,0)与直线l:x=3的各点连接的所有线段中,线段OA最短,长度为3,则d(O,直线x=3)=3.特别地,点P在图形W上,则点P到图形的距离为0,即d(P,图形W)=0.
①在平面直角坐标系中,原点O(0,0)与直线l:y=x的距离d(O,y=x)= ;
②如图2,点P的坐标为(0,m)且d(p,y=2x﹣2)=,则m= .
五、解答题(共3小题,满分30分)
24.(8分)2022年上半年在抗击新冠肺炎疫情期间,全国上下万众一心为上海捐赠物资,某物流公司运送捐赠物资,已知用2辆A型车和1辆B型车装满货物一次可运货7吨;用1辆A型车和2辆B型车装满货物一次可运货8吨.
(1)求1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)该物流公司现有14吨货物需要运送,计划同时租用A型车a辆,B型车b辆(每种车辆至少1辆),一次运完且恰好每辆车都装满货物,请问有哪几种租车方案?
25.(10分)如图,在平面直角坐标系xOy中,点A(﹣1,0),B(0,3),点C在x轴上,且直线BC与直线AB关于y轴对称.
(1)求直线BC的解析式;
(2)若在直线AB上存在点P使S△BCP=,求点P的坐标;
(3)若点M是直线AB上一点,点N是y轴上一点,连接CM,CN,MN,使△CMN是以CM为腰的等腰直角三角形,直接写出点N的坐标.
26.(12分)如图1,在△ABC中,∠ACB=90°,AC=3,BC=4,将△ABC绕点A旋转得到△ADE.
(1)连接CD交直线AB于点P
①当AD=AP时,BP= .
②当△ACP为等腰三角形时,求BP的长.
(2)当点D恰好落在线段AB上时,如图2,连接CE,求CE的长.
2022-2023学年四川省成都市锦江区嘉祥外国语学校八年级(下)开学数学试卷
参考答案
一、选择题(共8小题,满分32分,每小题4分)
1.D; 2.C; 3.D; 4.D; 5.B; 6.C; 7.D; 8.D;
二、填空题(共5小题,满分20分,每小题4分)
9.x≥2; 10.9; 11.y=x+5; 12.; 13.;
三、解答题(共3小题,满分28分)
14.(1)+2.
(2).; 15. ; 16.八; 40; 96; 96;
17.(1)见解答;
(2)3.; 18.(1)直线AB的解析式为:y=﹣x+;(2)P的坐标为(0,﹣2)或P(0,2+2)或P(0,2﹣2);(3)当线段A1B1与x轴有交点时,n的取值的最大值为2.;
四、填空题(共5小题,满分20分,每小题4分)
19.20; 20.﹣1≤b≤2; 21.4; 22.AF2+BE2=2DE2; 1; 23.0; 3或﹣7;
五、解答题(共3小题,满分30分)
24.(1)1辆A型车装满货物一次可运货2吨,1辆B型车装满货物一次可运货3吨;
(2)共有2种租车方案,方案1:租用A型车4辆,B型车2辆;方案2:租用A型车1辆,B型车4辆.; 25.(1)直线BC解析式为y=﹣3x+3;
(2)P的坐标为(,)或(﹣,);
(3)N的坐标为(0,)或(0,﹣4)或(0,﹣)或(0,).; 26.2;
一、选择题(共8小题,满分32分,每小题4分)
1.(4分)下列计算正确的是( )
A. B. C. D.
2.(4分)某中学演讲比赛中,进入决赛的七位选手的成绩分别为91、93、95、96、97、97、97,那么这组数据的众数和中位数分别是( )
A.93,96 B.97,97 C.97,96 D.93,97
3.(4分)下列各组数中不能作为直角三角形的三边长的是( )
A.6、8、10 B.9、12、15 C.7、24、25 D.、、
4.(4分)若点P(m﹣1,5)与点Q(3,2﹣n)关于x轴对称,则m+n的值是( )
A.1 B.3 C.5 D.11
5.(4分)将一副直角三角板(∠A=∠FDE=90°,∠F=45°,∠C=60°,点D在边AB上)按图中所示位置摆放,两条斜边为EF,BC,且EF∥BC,则∠ADF等于
( )
A.70° B.75° C.80° D.85°
6.(4分)育才中学初一年级某班为奖励在校运动会上取得好成绩的同学,花了184元购买甲、乙两种奖品共20件.其中甲种奖品每件8元,乙种奖品每件6元,若设购买甲种奖品x件,乙种奖品y件,则所列方程组正确的是( )
A. B.
C. D.
7.(4分)如图,在△ABC中,∠B=90°,AB=6,BC=8,AD为∠BAC的角平分线,则三角形ADC的面积为( )
A.3 B.10 C.12 D.15
8.(4分)已知一次函数y1=ax+b和y2=bx+a(ab≠0且a≠b),这两个函数的图象可能是( )
A. B.
C. D.
二、填空题(共5小题,满分20分,每小题4分)
9.(4分)二次根式中,x的取值范围是 .
10.(4分)已知y=﹣+2,则xy= .
11.(4分)已知一次函数的图象经过点(0,5),且与直线y=x平行,则一次函数的表达式为 .
12.(4分)如图所示的圆柱体中底面圆的半径是,高为3,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是 .(结果保留根号)
13.(4分)如图,已知函数y=ax+b和y=cx+d图象交于点M,则根据图象可知,关于x、y的二元一次方程组的解为 .
三、解答题(共3小题,满分28分)
14.(12分)计算下列各题:
(1)计算:6×+(π﹣2019)0﹣|5﹣|﹣()﹣2;
(2)解方程组:.
15.(8分)如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;
(3)P为x轴上一动点,当AP+CP有最小值时,求这个最小值.
16.(8分)疫情防控人人有责,为此我校在七、八年级举行了“新冠疫情防控”知识竞赛,从七、八年级各随机抽取了10名学生进行比赛(百分制),测试成绩整理、描述和分析如下:
(成绩得分用x表示,共分成四组:A.80≤x<85,B.85≤x<90,C.90≤x<95,D:95≤x≤100)
七年级10名学生的成绩是:96,80,96,86,99,96,90,100,99,82.
八年级10名学生的成绩在C组中的数据是:94,90,92.
七、八年级抽取的学生竞赛成绩统计表
年级 平均数 中位数 众数 方差
七年级 92.4 b c 52
八年级 92 93 100 50.4
根据以上信息,解答下列问题:
(1)这次比赛中 年级成绩更平衡,更稳定;
(2)直接写出上述a、b、c的值:a= ,b= ,c= ;
(3)我校八年级共1200人参加了此次调查活动,估计参加此次调查活动成绩优秀(x≥90)的八年级学生人数是多少?
17.(10分)如图,将长方形ABCD沿对角线AC翻折,点B落在点E处,EC交AD于点F.
(1)求证:△AEF≌△CDF;
(2)若AB=4,BC=8,求DF的长.
18.(10分)已知平面直角坐标系中,直线AB图象上有两点 和点B(5,),与x轴交于点C,与y轴交于点D.
(1)求直线AB的表达式;
(2)若在y轴上有一异于原点的点P,使△PAB为等腰三角形,求点P的坐标;
(3)若将线段AB沿直线y=mx+n(m≠0)进行对折得到线段A1B1,且点A1始终在直线OA上,当线段A1B1与x轴有交点时,求n的取值的最大值.
四、填空题(共5小题,满分20分,每小题4分)
19.(4分)已知x=+2,y=﹣2,则x2+y2+2xy= .
20.(4分)如图,在平面直角坐标系中,点A,B的坐标分别为(1,1),(1,4),直线y=2x+b与线段AB有公共点,则b的取值范围是 .
21.(4分)对于实数a,b,定义运算“◆”:a◆b=,例如3◆2,因为3>2,所以3◆2==,若x,y满足方程组,则(x◆y)◆x= .
22.(4分)在等腰直角三角形ABC中,∠ACB=90°,CD⊥AB于点D,点E是平面内任意一点,连接DE,如图1,当点E在边BC上时,过点D作DF⊥DE交AC于点F.
(1)线段AF,DE,BE之间满足的数量关系是 .
(2)如图2,当点E在△BDC内部时,连接AE,CE,若DB=5,DE=3,∠AED=45°,求线段CE的长为 .
23.(4分)定义:点P与图形W上各点连接的所有线段中,若线段PA最短,则线段PA的长度称为点P到图形W的距离,记为d(P,图形W).例如,在图1中,原点O(0,0)与直线l:x=3的各点连接的所有线段中,线段OA最短,长度为3,则d(O,直线x=3)=3.特别地,点P在图形W上,则点P到图形的距离为0,即d(P,图形W)=0.
①在平面直角坐标系中,原点O(0,0)与直线l:y=x的距离d(O,y=x)= ;
②如图2,点P的坐标为(0,m)且d(p,y=2x﹣2)=,则m= .
五、解答题(共3小题,满分30分)
24.(8分)2022年上半年在抗击新冠肺炎疫情期间,全国上下万众一心为上海捐赠物资,某物流公司运送捐赠物资,已知用2辆A型车和1辆B型车装满货物一次可运货7吨;用1辆A型车和2辆B型车装满货物一次可运货8吨.
(1)求1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)该物流公司现有14吨货物需要运送,计划同时租用A型车a辆,B型车b辆(每种车辆至少1辆),一次运完且恰好每辆车都装满货物,请问有哪几种租车方案?
25.(10分)如图,在平面直角坐标系xOy中,点A(﹣1,0),B(0,3),点C在x轴上,且直线BC与直线AB关于y轴对称.
(1)求直线BC的解析式;
(2)若在直线AB上存在点P使S△BCP=,求点P的坐标;
(3)若点M是直线AB上一点,点N是y轴上一点,连接CM,CN,MN,使△CMN是以CM为腰的等腰直角三角形,直接写出点N的坐标.
26.(12分)如图1,在△ABC中,∠ACB=90°,AC=3,BC=4,将△ABC绕点A旋转得到△ADE.
(1)连接CD交直线AB于点P
①当AD=AP时,BP= .
②当△ACP为等腰三角形时,求BP的长.
(2)当点D恰好落在线段AB上时,如图2,连接CE,求CE的长.
2022-2023学年四川省成都市锦江区嘉祥外国语学校八年级(下)开学数学试卷
参考答案
一、选择题(共8小题,满分32分,每小题4分)
1.D; 2.C; 3.D; 4.D; 5.B; 6.C; 7.D; 8.D;
二、填空题(共5小题,满分20分,每小题4分)
9.x≥2; 10.9; 11.y=x+5; 12.; 13.;
三、解答题(共3小题,满分28分)
14.(1)+2.
(2).; 15. ; 16.八; 40; 96; 96;
17.(1)见解答;
(2)3.; 18.(1)直线AB的解析式为:y=﹣x+;(2)P的坐标为(0,﹣2)或P(0,2+2)或P(0,2﹣2);(3)当线段A1B1与x轴有交点时,n的取值的最大值为2.;
四、填空题(共5小题,满分20分,每小题4分)
19.20; 20.﹣1≤b≤2; 21.4; 22.AF2+BE2=2DE2; 1; 23.0; 3或﹣7;
五、解答题(共3小题,满分30分)
24.(1)1辆A型车装满货物一次可运货2吨,1辆B型车装满货物一次可运货3吨;
(2)共有2种租车方案,方案1:租用A型车4辆,B型车2辆;方案2:租用A型车1辆,B型车4辆.; 25.(1)直线BC解析式为y=﹣3x+3;
(2)P的坐标为(,)或(﹣,);
(3)N的坐标为(0,)或(0,﹣4)或(0,﹣)或(0,).; 26.2;
同课章节目录
