2022-2023学年沪科版九年级上册数学期末复习试卷(无答案)
文档属性
| 名称 | 2022-2023学年沪科版九年级上册数学期末复习试卷(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 337.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-29 00:00:00 | ||
图片预览


文档简介
2023-2024学年沪科版九年级上册数学期末复习试卷
一.选择题(共10小题,满分40分,每小题4分)
1.边长为5的正方形ABCD,点F是BC上一动点,过对角线交点E作EG⊥EF,交CD于点G,设BF的长为x,△EFG的面积为y,则y与x满足的函数关系是( )
A.正比例函数 B.一次函数 C.二次函数 D.以上都不是
2对于二次函数,下列说法,不正确的是( )
A. 抛物线的开口向下 B. 当时,y随x的增大而减小
C. 图象是轴对称图形 D. 当时,y有最大值3
3如图,小正方形的边长均为1,则图中三角形阴影部分与相似的是( )
A. B. C. D.
4.抛物线y=x2﹣2与y轴交点的坐标是( )
A.(0,2) B.(0,﹣2) C.(2,0) D.(﹣2,0)
5.如图,在中,,,则的值为( )
A.2 B.3 C. D.
6如果实数,,,满足,下列四个选项中,正确的是( )
A. B. C. D.
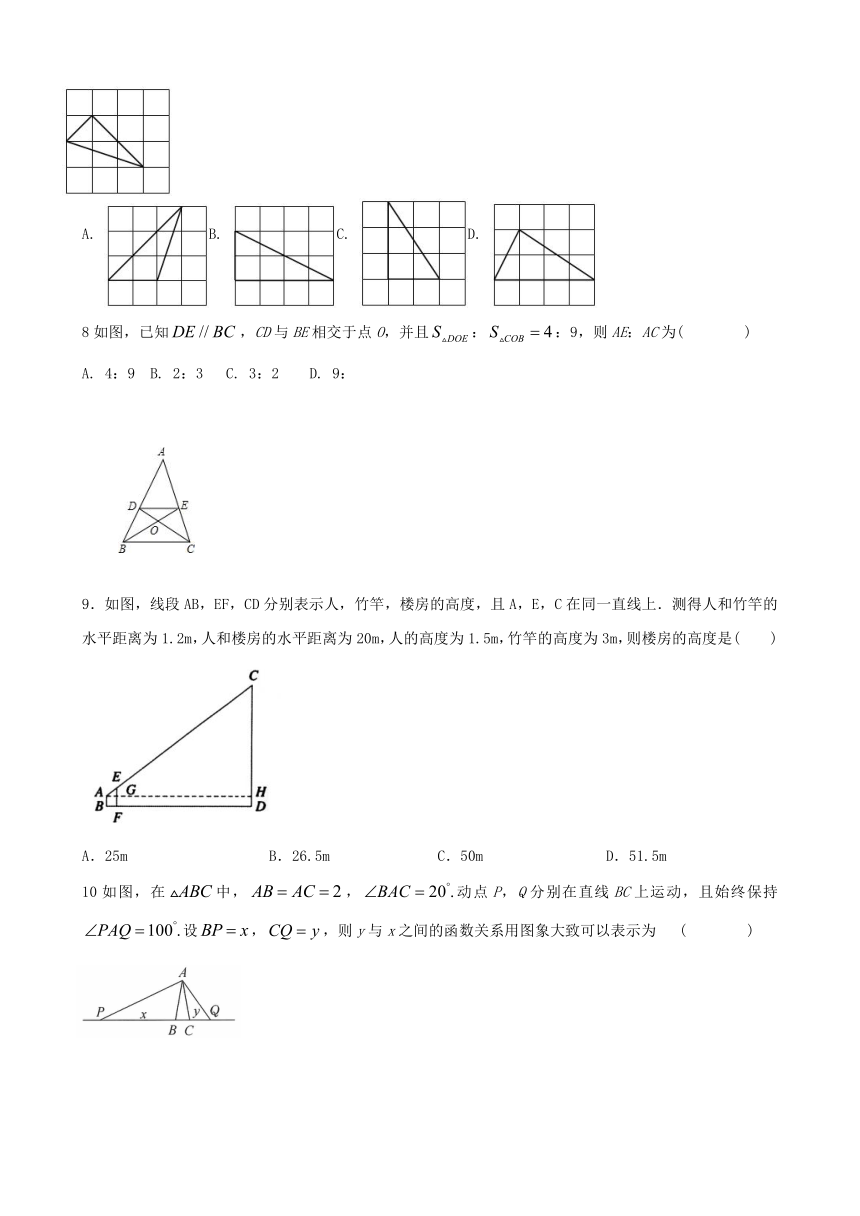
7下列的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与如图的三角形相似的是( )
A. B. C. D.
8如图,已知,CD与BE相交于点O,并且::9,则AE:AC为( )
A. 4:9 B. 2:3 C. 3:2 D. 9:
9.如图,线段AB,EF,CD分别表示人,竹竿,楼房的高度,且A,E,C在同一直线上.测得人和竹竿的水平距离为1.2m,人和楼房的水平距离为20m,人的高度为1.5m,竹竿的高度为3m,则楼房的高度是( )
A.25m B.26.5m C.50m D.51.5m
10如图,在中,,动点P,Q分别在直线BC上运动,且始终保持设,,则y与x之间的函数关系用图象大致可以表示为 ( )
A. B. C. D.
二.填空题(共4小题,满分20分,每小题5分)
1.若n(n≠0)是关于x的方程x2+mx+2n=0的根,则m+n= .
2.在Rt△ABC中,∠C=90°,AB=4,BC=3,则sinA的值是 .
3.如果函数y=x2+4x﹣m的图象与x轴有公共点,那么m的取值范围是 .
4.如图,正方形ABCD和正方形CGFE的顶点C,D,E在同一条直线上,顶点B,C,G在同一条直线上.O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接FH交EG于点M,连接OH.以下四个结论,其中正确的结论有 .
A.GH⊥BE
B.△EHM∽△GHF
C.﹣1
D.=2﹣
三.解答题( 满分90分)
1求下列各式的值:
.
2如图,直线分别交x轴,y轴于点A,B,抛物线的顶点为C,连接AC,
求出A,B,C三点的坐标;
求出的面积.
3如图,在中,,AB的垂直平分线与BC,AB的交点分别为D,若,,求AC的长和的值.
4如图,在平面直角坐标系中,的三个顶点坐标分别为,,以点O为位似中心,位似比为2:1,在y轴的左侧画出放大后的,并直接写出,的坐标.
5已知:如图三个顶点的坐标分别为、、,正方形网格中,每个小正方形的边长是1个单位长度.
以点C为位似中心,在网格中画出,使与的位似比为2:1,并直接写出点的坐标;
与的面积比为______.
6.如图,曲线BC是反比例函数 的一部分,其中B(2,2-m),C(4,-m),抛物线 的顶点记作A.
(1)求k的值;
(2)甲同学说,点A可以与点B重合;而乙同学说,点A也可以与点C重合,甲、乙的说法对吗?请说明理由.
7.如图,在中,是边上的中线,分别过点C,点D作的平行线交于E点,与交于点连接.
(1)求证:四边形是菱形;
(2)若,求的值.
8.跳绳时,绳甩到最高处时的形状是抛物线. 正在甩绳的甲、乙两名同学拿绳的手间距AB为6米,到地面的距离AO和BD均为0. 9米,身高为1. 4米的小丽站在距点O的水平距离为1米的点F处,绳子甩到最高处时刚好通过她的头顶点E. 以点O为原点建立如图所示的平面直角坐标系, 设此抛物线的解析式为 y=ax2+bx+0.9.
(1)求该抛物线的解析式;
(2)如果身高为1. 85米的小华也想参加跳绳,问绳子能否顺利从他头顶越过?请说明理由;
(3)如果一群身高在1. 4米到1. 7米之间的人站在OD之间,且离点O的距离为t米, 绳子甩到最高处时必须超过他们的头顶,请结合图像,写出t的取值范围 .
一.选择题(共10小题,满分40分,每小题4分)
1.边长为5的正方形ABCD,点F是BC上一动点,过对角线交点E作EG⊥EF,交CD于点G,设BF的长为x,△EFG的面积为y,则y与x满足的函数关系是( )
A.正比例函数 B.一次函数 C.二次函数 D.以上都不是
2对于二次函数,下列说法,不正确的是( )
A. 抛物线的开口向下 B. 当时,y随x的增大而减小
C. 图象是轴对称图形 D. 当时,y有最大值3
3如图,小正方形的边长均为1,则图中三角形阴影部分与相似的是( )
A. B. C. D.
4.抛物线y=x2﹣2与y轴交点的坐标是( )
A.(0,2) B.(0,﹣2) C.(2,0) D.(﹣2,0)
5.如图,在中,,,则的值为( )
A.2 B.3 C. D.
6如果实数,,,满足,下列四个选项中,正确的是( )
A. B. C. D.
7下列的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与如图的三角形相似的是( )
A. B. C. D.
8如图,已知,CD与BE相交于点O,并且::9,则AE:AC为( )
A. 4:9 B. 2:3 C. 3:2 D. 9:
9.如图,线段AB,EF,CD分别表示人,竹竿,楼房的高度,且A,E,C在同一直线上.测得人和竹竿的水平距离为1.2m,人和楼房的水平距离为20m,人的高度为1.5m,竹竿的高度为3m,则楼房的高度是( )
A.25m B.26.5m C.50m D.51.5m
10如图,在中,,动点P,Q分别在直线BC上运动,且始终保持设,,则y与x之间的函数关系用图象大致可以表示为 ( )
A. B. C. D.
二.填空题(共4小题,满分20分,每小题5分)
1.若n(n≠0)是关于x的方程x2+mx+2n=0的根,则m+n= .
2.在Rt△ABC中,∠C=90°,AB=4,BC=3,则sinA的值是 .
3.如果函数y=x2+4x﹣m的图象与x轴有公共点,那么m的取值范围是 .
4.如图,正方形ABCD和正方形CGFE的顶点C,D,E在同一条直线上,顶点B,C,G在同一条直线上.O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接FH交EG于点M,连接OH.以下四个结论,其中正确的结论有 .
A.GH⊥BE
B.△EHM∽△GHF
C.﹣1
D.=2﹣
三.解答题( 满分90分)
1求下列各式的值:
.
2如图,直线分别交x轴,y轴于点A,B,抛物线的顶点为C,连接AC,
求出A,B,C三点的坐标;
求出的面积.
3如图,在中,,AB的垂直平分线与BC,AB的交点分别为D,若,,求AC的长和的值.
4如图,在平面直角坐标系中,的三个顶点坐标分别为,,以点O为位似中心,位似比为2:1,在y轴的左侧画出放大后的,并直接写出,的坐标.
5已知:如图三个顶点的坐标分别为、、,正方形网格中,每个小正方形的边长是1个单位长度.
以点C为位似中心,在网格中画出,使与的位似比为2:1,并直接写出点的坐标;
与的面积比为______.
6.如图,曲线BC是反比例函数 的一部分,其中B(2,2-m),C(4,-m),抛物线 的顶点记作A.
(1)求k的值;
(2)甲同学说,点A可以与点B重合;而乙同学说,点A也可以与点C重合,甲、乙的说法对吗?请说明理由.
7.如图,在中,是边上的中线,分别过点C,点D作的平行线交于E点,与交于点连接.
(1)求证:四边形是菱形;
(2)若,求的值.
8.跳绳时,绳甩到最高处时的形状是抛物线. 正在甩绳的甲、乙两名同学拿绳的手间距AB为6米,到地面的距离AO和BD均为0. 9米,身高为1. 4米的小丽站在距点O的水平距离为1米的点F处,绳子甩到最高处时刚好通过她的头顶点E. 以点O为原点建立如图所示的平面直角坐标系, 设此抛物线的解析式为 y=ax2+bx+0.9.
(1)求该抛物线的解析式;
(2)如果身高为1. 85米的小华也想参加跳绳,问绳子能否顺利从他头顶越过?请说明理由;
(3)如果一群身高在1. 4米到1. 7米之间的人站在OD之间,且离点O的距离为t米, 绳子甩到最高处时必须超过他们的头顶,请结合图像,写出t的取值范围 .
同课章节目录
