2023-2024学年上海市杨浦区七年级(上)期末数学模拟试卷(五四学制)(含答案)
文档属性
| 名称 | 2023-2024学年上海市杨浦区七年级(上)期末数学模拟试卷(五四学制)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 227.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-29 17:31:41 | ||
图片预览



文档简介
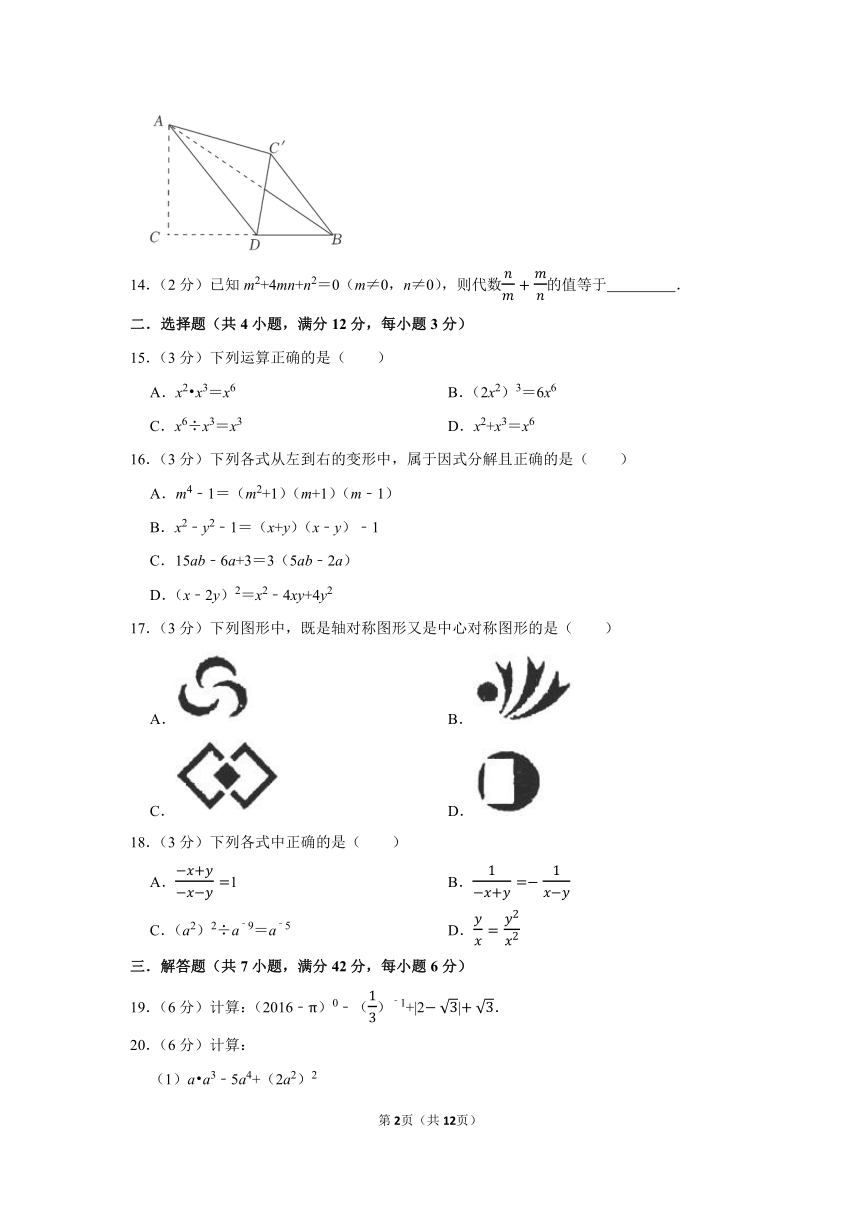
2023-2024学年上海市杨浦区七年级(上)期末数学模拟试卷(五四学制)
一.填空题(共14小题,满分28分,每小题2分)
1.(2分)列式表示:p的7倍是 .
2.(2分)把0.00302用科学记数法表示为 .
3.(2分)计算:(2a2b3)2= .
4.(2分)若(x+3)(x﹣3)=x2+px﹣9,则p的值是 .
5.(2分)化简: .
6.(2分)添上“+”或“﹣”号:﹣x2+8x﹣16= (x2﹣8x+16).
7.(2分)如图,将一个长方形ABCD分成4个小长方形,其中②与③的大小形状相同,已知BC=1,则①与④两个小长方形的周长之和为 .
8.(2分)如果单项式3xm+1y3与x4y1﹣n是同类项,则nm= .
9.(2分)当x ,分式无意义.
10.(2分)若x2+(a﹣1)x+25是一个完全平方式,则a= .
11.(2分)若(x﹣1)(x+6)=x2+mx﹣6,则m2﹣4的结果为 .
12.(2分)如图是一台水泵的叶轮平面示意图,它绕着圆心O旋转最小度数为 后可以与自身重合.
13.(2分)如图,在Rt△ABC中,∠C=90°,AC=6,BC=16,点D为BC边上的中点,将△ACD沿AD对折,使点C落在同一平面内的点C′处,连接BC′,则BC′的长为 .
14.(2分)已知m2+4mn+n2=0(m≠0,n≠0),则代数的值等于 .
二.选择题(共4小题,满分12分,每小题3分)
15.(3分)下列运算正确的是( )
A.x2 x3=x6 B.(2x2)3=6x6
C.x6÷x3=x3 D.x2+x3=x6
16.(3分)下列各式从左到右的变形中,属于因式分解且正确的是( )
A.m4﹣1=(m2+1)(m+1)(m﹣1)
B.x2﹣y2﹣1=(x+y)(x﹣y)﹣1
C.15ab﹣6a+3=3(5ab﹣2a)
D.(x﹣2y)2=x2﹣4xy+4y2
17.(3分)下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
18.(3分)下列各式中正确的是( )
A.1 B.
C.(a2)2÷a﹣9=a﹣5 D.
三.解答题(共7小题,满分42分,每小题6分)
19.(6分)计算:(2016﹣π)0﹣()﹣1+|2|.
20.(6分)计算:
(1)a a3﹣5a4+(2a2)2
(2)6x(x﹣3y)
(3)(x﹣2)(x+3)
(4)(28a3﹣14a2+7a)÷7a
21.(6分)分解因式:a3+3a2+3a+2.
22.(6分)x5+2x3﹣x﹣2.
23.(6分)解分式方程
(1)2
(2)1
24.(6分)化简下列各式,使结果只含有正整数指数幂.
(1)(﹣3m2n﹣3)﹣2 (﹣2m﹣1n2)﹣3
(2)(2m2n﹣3)3÷(﹣mn﹣2)﹣2.
25.(6分)先化简,再求值:(1)÷(x),其中x=2.
四.解答题(共3小题,满分18分,每小题6分)
26.(6分)如图,每个小方格都是边长为1个单位长度的小正方形.
(1)在方格纸中,格点三角形ABC经过旋转后得到格点三角形A1B1C1,则旋转中心是 (填序号).
(2)说明三角形A2B2C2是由三角形ABC经过每样的平移得到的?
(3)画出三角形A1B1C1关于直线MN成轴对称的三角形A3B3C3.
27.(6分)在现代医学中,呼吸机是一种能够挽救及延长病人生命的至关重要的医疗设备.某医院准备购进一批呼吸机,现有A,B两种品牌呼吸机可供选择.已知每台A品牌呼吸机比每台B品牌呼吸机的进价多0.2万元,用20万元购买A品牌呼吸机的数量和用18万元购买B品牌呼吸机的数量相同.求A,B两种品牌的呼吸机每台的进价各是多少万元?
28.(6分)问题提出
(1)如图①,已知正方形ABCD的边长为4,E是BC的中点,将线段AE绕点E顺时针旋转90°得到线段FE,连接CF,求CF的长;
问题解决
(2)为了解乡村生活、体验乡村水土风情、享受田园风光,某校计划利用空地修建蔬菜种植基地,让学生自己种植,自己管理,学习种植技术,体验丰收的喜悦.已知蔬菜种植基地ABCD的设计示意图如图②所示,其中AD∥BC,BC=CD=100m,∠C=60°,E为CD上一点,且不与C,D重合,∠AEB=60°.按设计要求,△ABE中种植叶菜类,其余种植根茎类.设CE的长为x(m),蔬菜种植基地的面积为y(m2).
①求y与x之间的函数关系式;
②当种植叶菜类的面积恰好与根茎类的面积相等时,求AB的长.
2023-2024学年上海市杨浦区七年级(上)期末数学模拟试卷(五四学制)
参考答案与试题解析
一.填空题(共14小题,满分28分,每小题2分)
1.【解答】解:根据题意可知p的7倍是7p.
故答案为:7p.
2.【解答】解:0.00302=3.02×10﹣3,
故答案为:3.02×10﹣3.
3.【解答】解:(2a2b3)2=4a4b6.
故答案为:4a4b6.
4.【解答】解:∵(x+3)(x﹣3)=x2﹣9=x2+px﹣9,
∴p=0.
故答案为:0.
5.【解答】解:原式a﹣b,
故答案为:a﹣b.
6.【解答】解:﹣x2+8x﹣16=﹣(x2﹣8x+16).
故答案为:﹣.
7.【解答】解:设②和③宽为x,长为y,根据题意得,
①的周长为:2x+2(1﹣y),
④的周长为:2y+2(1﹣x),
所以,①与④两个小长方形的周长之和为:
2x+2(1﹣y)+2y+2(1﹣x)
=2x+2﹣2y+2y+2﹣2x
=4.
故答案为:4.
8.【解答】解:∵单项式3xm+1y3与x4y1﹣n是同类项,
∴m+1=4,1﹣n=3,
∴m=3,n=﹣2,
∴nm=(﹣2)3=﹣8,
故答案为:﹣8.
9.【解答】解:根据题意得:3x﹣6=0,
解得:x=2.
故答案为:=2.
10.【解答】解:∵x2+(a﹣1)x+25是一个完全平方式,
∴(a﹣1)x=±2 x 5=±10x,
∴a﹣1=±10,解得a=11或﹣9,
故答案为:11或﹣9.
11.【解答】解:由题意得x2+5x﹣6=x2+mx﹣6,
∴m=5,
∴m2﹣4=52﹣4=21.
故答案为:21.
12.【解答】解:把图形中的每个阴影部分与相邻的一个部分当作一个部分,因而整个圆周被分成8个完全相同的部分,
每个部分对应的圆心角是45度,因而最少旋转的度数是45度.
故答案为:45°.
13.【解答】解:连接CC',交AD于N,如图所示:
∵将△ACD沿AD对折,使点C落在同一平面内的点C'处,
∴AD⊥CC',CN=C'N,CD=C′D,
∵点D为BC边上的中点,
∴CDBC16=8,CD=BD=C′D,
∴AD10,
∵S△ACDAC CDAD CN,
∴CN,
∴CC′=2CN=2,
∵CD=BD=C′D,
∴∠DCC'=∠DC'C,∠DBC'=∠DC'B,
∵∠DCC'+∠DC'C+∠DBC'+∠DC'B=180°,
∴∠CC'B=∠CC'D+∠DC'B(∠DCC'+∠DC'C+∠DBC'+∠DC'B)=90°,
∴BC′,
故答案为:.
14.【解答】解:∵m2+4mn+n2=0,且m≠0,n≠0,
∴40,
则4,
故答案为:﹣4.
二.选择题(共4小题,满分12分,每小题3分)
15.【解答】解:A、x2 x3=x5,故错误,不合题意;
B、(2x2)3=8x6,故错误,不合题意;
C、x6÷x3=x3,故正确,符合题意;
D、x2+x3不能合并,故错误,不合题意;
故选:C.
16.【解答】解:A、m4﹣1=(m2+1)(m+1)(m﹣1),选项正确,符合题意;
B、x2﹣y2﹣1=(x+y)(x﹣y)﹣1,等式右边不是整式积的形式,不符合题意;
C、15ab﹣6a+3=3(5ab﹣2a+1),分解错误,不符合题意;
D、(x﹣2y)2=x2﹣4xy+4y2,是整式的乘法,不符合题意;
故选:A.
17.【解答】解:A.不是中心对称图形,也不是轴对称图形,故此选项不合题意;
B.不是中心对称图形,也不是轴对称图形,故此选项不合题意;
C.既是中心对称图形,也是轴对称图形,故此选项符合题意;
D.不是中心对称图形,是轴对称图形,故此选项不合题意;
故选:C.
18.【解答】解:A、,故本选项不符合题意;
B、,故本选项正确;
C、(a2)2÷a﹣9=a﹣13,故本选项不符合题意;
D、,故本选项不符合题意,
故选:B.
三.解答题(共7小题,满分42分,每小题6分)
19.【解答】解:(2016﹣π)0﹣()﹣1+|2|
=1﹣3+2
=0.
20.【解答】解:(1)a a3﹣5a4+(2a2)2
=a4﹣5a4+4a4
=0;
(2)6x(x﹣3y)=6x2﹣18xy;
(3)(x﹣2)(x+3)=x2+x﹣6;
(4)(28a3﹣14a2+7a)÷7a
=4a2﹣2a+1.
21.【解答】解:a3+3a2+3a+2
=a3+a2+a+2a2+2a+2
=a(a2+a+1)+2(a2+a+1)
=(a+2)(a2+a+1).
22.【解答】解:x5+2x3﹣x﹣2
=(x5﹣x)+(2x3﹣2)
=x(x4﹣1)+2(x3﹣1)
=(x﹣1)(x+1)(x2+1)x+2(x﹣1)(x2+x+1)
=(x﹣1)[x(x+1)(x2+1)+2x2+2x+2]
=(x﹣1)(x4+x3+x2+x+2x2+2x+2)
=(x﹣1)(x4+x3+3x2+3x+2)
23.【解答】解:(1)去分母得:x+1=2x﹣14,
解得:x=15,
经检验x=15是分式方程的解;
(2)去分母得:x2+2x+1﹣4=x2﹣1,
解得:x=1,
经检验x=1是增根,分式方程无解.
24.【解答】解:(1)(﹣3m2n﹣3)﹣2 (﹣2m﹣1n2)﹣3
=(﹣3)﹣2m﹣4n6 (﹣2)﹣3m3n﹣6
(2)(2m2n﹣3)3÷(﹣mn﹣2)﹣2
=8m6n﹣9÷m﹣2n4
=8m8n﹣13
25.【解答】解:原式=()÷[],
,
,
,
当x=2时,原式.
四.解答题(共3小题,满分18分,每小题6分)
26.【解答】解:(1)由题意可得,旋转中心是②,
故答案为:②;
(2)由题意可得,三角形A2B2C2是由三角形ABC先向右平移14个单位,然后向下平移2个单位得到的;
(3)如图所示,A3B3C3即为所求.
27.【解答】解:设B品牌的呼吸机每台的进价是x万元,则A品牌的呼吸机每台的进价是(x+0.2)万元,
依题意,得:,
解得:x=1.8,
经检验:x=1.8是原方程的解,且符合题意,
∴x+0.2=2.
答:A品牌的呼吸机每台的进价是2万元,B品牌的呼吸机每台的进价是1.8万元.
28.【解答】解:(1)取AB的中点R,连接ER,如图①所示:
∵四边形ABCD是边长为4的正方形,E是BC的中点,
∴AR=BR=BE=CEAB4=2,∠B=90°,
∴△EBR是等腰直角三角形,
∴REBE2=2,∠BRE=∠BER=45°,
∴∠RAE+∠REA=45°,
∵线段AE绕点E顺时针旋转90°得到线段FE,
∴FE=AE,∠AEF=90°,∠CEF+∠REA=180°﹣∠AEF﹣∠BER=180°﹣90°﹣45°=45°,
∴∠CEF=∠RAE,
在△CEF和△RAE中,
,
∴△CEF≌△RAE(SAS),
∴CF=RE=2;
(2)①过点E作EG⊥AD交AD延长线于G,延长GE交BC于F,如图②所示:
∵AD∥BC,
∴EF⊥BC,∠EDG=∠C=60°,
∴∠EDA=120°,
∵BC=CD=100m,
∴DE=(100﹣x)m,
在Rt△EFC中,EF=CE×sin60°x(m),
在Rt△EGD中,EG=DE×sin60°=(100﹣x)(m),
∴GF=EF+EGx+(100﹣x)50(m),
在BC上截取CN=CE,连接EN,
则△ECN为等边三角形,
∴EN=CN=CE=x m,∠ENC=∠CEN=60°,
∴∠BNE=120°=∠EDA,∠EBN+∠BEN=60°,
∵∠AED+∠BEN=180°﹣∠AEB﹣∠CEN=180°﹣60°﹣60°=60°,
∴∠EBN=∠AED,
∵BC﹣CN=CD﹣CE,
∴BN=ED,
在△BNE和△EDA中,
,
∴△BNE≌△EDA(ASA),
∴AD=EN=x m,BE=AE,
∴y(AD+BC) GF(x+100)×5025x+2500,(0<x<100),
∴y与x之间的函数关系式为:y=25x+2500,(0<x<100);
②当种植叶菜类的面积恰好与根茎类的面积相等时,即S△ADE+S△BECy,
∴x(100﹣x)100x(25x+2500),
整理得:(x﹣50)(x﹣100)=0,
∴x1=50,x2=100(不合题意舍去),
∴CE=50m,
∴EF50=25(m),
在Rt△EFC中,由勾股定理得:CF25(m),
∴BF=BC﹣CF=100﹣25=75(m),
在Rt△EFB中,由勾股定理得:BE50(m),
∵AE=BE,∠AEB=60°,
∴△ABE是等边三角形,
∴AB=BE=50m.
第1页(共1页)
一.填空题(共14小题,满分28分,每小题2分)
1.(2分)列式表示:p的7倍是 .
2.(2分)把0.00302用科学记数法表示为 .
3.(2分)计算:(2a2b3)2= .
4.(2分)若(x+3)(x﹣3)=x2+px﹣9,则p的值是 .
5.(2分)化简: .
6.(2分)添上“+”或“﹣”号:﹣x2+8x﹣16= (x2﹣8x+16).
7.(2分)如图,将一个长方形ABCD分成4个小长方形,其中②与③的大小形状相同,已知BC=1,则①与④两个小长方形的周长之和为 .
8.(2分)如果单项式3xm+1y3与x4y1﹣n是同类项,则nm= .
9.(2分)当x ,分式无意义.
10.(2分)若x2+(a﹣1)x+25是一个完全平方式,则a= .
11.(2分)若(x﹣1)(x+6)=x2+mx﹣6,则m2﹣4的结果为 .
12.(2分)如图是一台水泵的叶轮平面示意图,它绕着圆心O旋转最小度数为 后可以与自身重合.
13.(2分)如图,在Rt△ABC中,∠C=90°,AC=6,BC=16,点D为BC边上的中点,将△ACD沿AD对折,使点C落在同一平面内的点C′处,连接BC′,则BC′的长为 .
14.(2分)已知m2+4mn+n2=0(m≠0,n≠0),则代数的值等于 .
二.选择题(共4小题,满分12分,每小题3分)
15.(3分)下列运算正确的是( )
A.x2 x3=x6 B.(2x2)3=6x6
C.x6÷x3=x3 D.x2+x3=x6
16.(3分)下列各式从左到右的变形中,属于因式分解且正确的是( )
A.m4﹣1=(m2+1)(m+1)(m﹣1)
B.x2﹣y2﹣1=(x+y)(x﹣y)﹣1
C.15ab﹣6a+3=3(5ab﹣2a)
D.(x﹣2y)2=x2﹣4xy+4y2
17.(3分)下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
18.(3分)下列各式中正确的是( )
A.1 B.
C.(a2)2÷a﹣9=a﹣5 D.
三.解答题(共7小题,满分42分,每小题6分)
19.(6分)计算:(2016﹣π)0﹣()﹣1+|2|.
20.(6分)计算:
(1)a a3﹣5a4+(2a2)2
(2)6x(x﹣3y)
(3)(x﹣2)(x+3)
(4)(28a3﹣14a2+7a)÷7a
21.(6分)分解因式:a3+3a2+3a+2.
22.(6分)x5+2x3﹣x﹣2.
23.(6分)解分式方程
(1)2
(2)1
24.(6分)化简下列各式,使结果只含有正整数指数幂.
(1)(﹣3m2n﹣3)﹣2 (﹣2m﹣1n2)﹣3
(2)(2m2n﹣3)3÷(﹣mn﹣2)﹣2.
25.(6分)先化简,再求值:(1)÷(x),其中x=2.
四.解答题(共3小题,满分18分,每小题6分)
26.(6分)如图,每个小方格都是边长为1个单位长度的小正方形.
(1)在方格纸中,格点三角形ABC经过旋转后得到格点三角形A1B1C1,则旋转中心是 (填序号).
(2)说明三角形A2B2C2是由三角形ABC经过每样的平移得到的?
(3)画出三角形A1B1C1关于直线MN成轴对称的三角形A3B3C3.
27.(6分)在现代医学中,呼吸机是一种能够挽救及延长病人生命的至关重要的医疗设备.某医院准备购进一批呼吸机,现有A,B两种品牌呼吸机可供选择.已知每台A品牌呼吸机比每台B品牌呼吸机的进价多0.2万元,用20万元购买A品牌呼吸机的数量和用18万元购买B品牌呼吸机的数量相同.求A,B两种品牌的呼吸机每台的进价各是多少万元?
28.(6分)问题提出
(1)如图①,已知正方形ABCD的边长为4,E是BC的中点,将线段AE绕点E顺时针旋转90°得到线段FE,连接CF,求CF的长;
问题解决
(2)为了解乡村生活、体验乡村水土风情、享受田园风光,某校计划利用空地修建蔬菜种植基地,让学生自己种植,自己管理,学习种植技术,体验丰收的喜悦.已知蔬菜种植基地ABCD的设计示意图如图②所示,其中AD∥BC,BC=CD=100m,∠C=60°,E为CD上一点,且不与C,D重合,∠AEB=60°.按设计要求,△ABE中种植叶菜类,其余种植根茎类.设CE的长为x(m),蔬菜种植基地的面积为y(m2).
①求y与x之间的函数关系式;
②当种植叶菜类的面积恰好与根茎类的面积相等时,求AB的长.
2023-2024学年上海市杨浦区七年级(上)期末数学模拟试卷(五四学制)
参考答案与试题解析
一.填空题(共14小题,满分28分,每小题2分)
1.【解答】解:根据题意可知p的7倍是7p.
故答案为:7p.
2.【解答】解:0.00302=3.02×10﹣3,
故答案为:3.02×10﹣3.
3.【解答】解:(2a2b3)2=4a4b6.
故答案为:4a4b6.
4.【解答】解:∵(x+3)(x﹣3)=x2﹣9=x2+px﹣9,
∴p=0.
故答案为:0.
5.【解答】解:原式a﹣b,
故答案为:a﹣b.
6.【解答】解:﹣x2+8x﹣16=﹣(x2﹣8x+16).
故答案为:﹣.
7.【解答】解:设②和③宽为x,长为y,根据题意得,
①的周长为:2x+2(1﹣y),
④的周长为:2y+2(1﹣x),
所以,①与④两个小长方形的周长之和为:
2x+2(1﹣y)+2y+2(1﹣x)
=2x+2﹣2y+2y+2﹣2x
=4.
故答案为:4.
8.【解答】解:∵单项式3xm+1y3与x4y1﹣n是同类项,
∴m+1=4,1﹣n=3,
∴m=3,n=﹣2,
∴nm=(﹣2)3=﹣8,
故答案为:﹣8.
9.【解答】解:根据题意得:3x﹣6=0,
解得:x=2.
故答案为:=2.
10.【解答】解:∵x2+(a﹣1)x+25是一个完全平方式,
∴(a﹣1)x=±2 x 5=±10x,
∴a﹣1=±10,解得a=11或﹣9,
故答案为:11或﹣9.
11.【解答】解:由题意得x2+5x﹣6=x2+mx﹣6,
∴m=5,
∴m2﹣4=52﹣4=21.
故答案为:21.
12.【解答】解:把图形中的每个阴影部分与相邻的一个部分当作一个部分,因而整个圆周被分成8个完全相同的部分,
每个部分对应的圆心角是45度,因而最少旋转的度数是45度.
故答案为:45°.
13.【解答】解:连接CC',交AD于N,如图所示:
∵将△ACD沿AD对折,使点C落在同一平面内的点C'处,
∴AD⊥CC',CN=C'N,CD=C′D,
∵点D为BC边上的中点,
∴CDBC16=8,CD=BD=C′D,
∴AD10,
∵S△ACDAC CDAD CN,
∴CN,
∴CC′=2CN=2,
∵CD=BD=C′D,
∴∠DCC'=∠DC'C,∠DBC'=∠DC'B,
∵∠DCC'+∠DC'C+∠DBC'+∠DC'B=180°,
∴∠CC'B=∠CC'D+∠DC'B(∠DCC'+∠DC'C+∠DBC'+∠DC'B)=90°,
∴BC′,
故答案为:.
14.【解答】解:∵m2+4mn+n2=0,且m≠0,n≠0,
∴40,
则4,
故答案为:﹣4.
二.选择题(共4小题,满分12分,每小题3分)
15.【解答】解:A、x2 x3=x5,故错误,不合题意;
B、(2x2)3=8x6,故错误,不合题意;
C、x6÷x3=x3,故正确,符合题意;
D、x2+x3不能合并,故错误,不合题意;
故选:C.
16.【解答】解:A、m4﹣1=(m2+1)(m+1)(m﹣1),选项正确,符合题意;
B、x2﹣y2﹣1=(x+y)(x﹣y)﹣1,等式右边不是整式积的形式,不符合题意;
C、15ab﹣6a+3=3(5ab﹣2a+1),分解错误,不符合题意;
D、(x﹣2y)2=x2﹣4xy+4y2,是整式的乘法,不符合题意;
故选:A.
17.【解答】解:A.不是中心对称图形,也不是轴对称图形,故此选项不合题意;
B.不是中心对称图形,也不是轴对称图形,故此选项不合题意;
C.既是中心对称图形,也是轴对称图形,故此选项符合题意;
D.不是中心对称图形,是轴对称图形,故此选项不合题意;
故选:C.
18.【解答】解:A、,故本选项不符合题意;
B、,故本选项正确;
C、(a2)2÷a﹣9=a﹣13,故本选项不符合题意;
D、,故本选项不符合题意,
故选:B.
三.解答题(共7小题,满分42分,每小题6分)
19.【解答】解:(2016﹣π)0﹣()﹣1+|2|
=1﹣3+2
=0.
20.【解答】解:(1)a a3﹣5a4+(2a2)2
=a4﹣5a4+4a4
=0;
(2)6x(x﹣3y)=6x2﹣18xy;
(3)(x﹣2)(x+3)=x2+x﹣6;
(4)(28a3﹣14a2+7a)÷7a
=4a2﹣2a+1.
21.【解答】解:a3+3a2+3a+2
=a3+a2+a+2a2+2a+2
=a(a2+a+1)+2(a2+a+1)
=(a+2)(a2+a+1).
22.【解答】解:x5+2x3﹣x﹣2
=(x5﹣x)+(2x3﹣2)
=x(x4﹣1)+2(x3﹣1)
=(x﹣1)(x+1)(x2+1)x+2(x﹣1)(x2+x+1)
=(x﹣1)[x(x+1)(x2+1)+2x2+2x+2]
=(x﹣1)(x4+x3+x2+x+2x2+2x+2)
=(x﹣1)(x4+x3+3x2+3x+2)
23.【解答】解:(1)去分母得:x+1=2x﹣14,
解得:x=15,
经检验x=15是分式方程的解;
(2)去分母得:x2+2x+1﹣4=x2﹣1,
解得:x=1,
经检验x=1是增根,分式方程无解.
24.【解答】解:(1)(﹣3m2n﹣3)﹣2 (﹣2m﹣1n2)﹣3
=(﹣3)﹣2m﹣4n6 (﹣2)﹣3m3n﹣6
(2)(2m2n﹣3)3÷(﹣mn﹣2)﹣2
=8m6n﹣9÷m﹣2n4
=8m8n﹣13
25.【解答】解:原式=()÷[],
,
,
,
当x=2时,原式.
四.解答题(共3小题,满分18分,每小题6分)
26.【解答】解:(1)由题意可得,旋转中心是②,
故答案为:②;
(2)由题意可得,三角形A2B2C2是由三角形ABC先向右平移14个单位,然后向下平移2个单位得到的;
(3)如图所示,A3B3C3即为所求.
27.【解答】解:设B品牌的呼吸机每台的进价是x万元,则A品牌的呼吸机每台的进价是(x+0.2)万元,
依题意,得:,
解得:x=1.8,
经检验:x=1.8是原方程的解,且符合题意,
∴x+0.2=2.
答:A品牌的呼吸机每台的进价是2万元,B品牌的呼吸机每台的进价是1.8万元.
28.【解答】解:(1)取AB的中点R,连接ER,如图①所示:
∵四边形ABCD是边长为4的正方形,E是BC的中点,
∴AR=BR=BE=CEAB4=2,∠B=90°,
∴△EBR是等腰直角三角形,
∴REBE2=2,∠BRE=∠BER=45°,
∴∠RAE+∠REA=45°,
∵线段AE绕点E顺时针旋转90°得到线段FE,
∴FE=AE,∠AEF=90°,∠CEF+∠REA=180°﹣∠AEF﹣∠BER=180°﹣90°﹣45°=45°,
∴∠CEF=∠RAE,
在△CEF和△RAE中,
,
∴△CEF≌△RAE(SAS),
∴CF=RE=2;
(2)①过点E作EG⊥AD交AD延长线于G,延长GE交BC于F,如图②所示:
∵AD∥BC,
∴EF⊥BC,∠EDG=∠C=60°,
∴∠EDA=120°,
∵BC=CD=100m,
∴DE=(100﹣x)m,
在Rt△EFC中,EF=CE×sin60°x(m),
在Rt△EGD中,EG=DE×sin60°=(100﹣x)(m),
∴GF=EF+EGx+(100﹣x)50(m),
在BC上截取CN=CE,连接EN,
则△ECN为等边三角形,
∴EN=CN=CE=x m,∠ENC=∠CEN=60°,
∴∠BNE=120°=∠EDA,∠EBN+∠BEN=60°,
∵∠AED+∠BEN=180°﹣∠AEB﹣∠CEN=180°﹣60°﹣60°=60°,
∴∠EBN=∠AED,
∵BC﹣CN=CD﹣CE,
∴BN=ED,
在△BNE和△EDA中,
,
∴△BNE≌△EDA(ASA),
∴AD=EN=x m,BE=AE,
∴y(AD+BC) GF(x+100)×5025x+2500,(0<x<100),
∴y与x之间的函数关系式为:y=25x+2500,(0<x<100);
②当种植叶菜类的面积恰好与根茎类的面积相等时,即S△ADE+S△BECy,
∴x(100﹣x)100x(25x+2500),
整理得:(x﹣50)(x﹣100)=0,
∴x1=50,x2=100(不合题意舍去),
∴CE=50m,
∴EF50=25(m),
在Rt△EFC中,由勾股定理得:CF25(m),
∴BF=BC﹣CF=100﹣25=75(m),
在Rt△EFB中,由勾股定理得:BE50(m),
∵AE=BE,∠AEB=60°,
∴△ABE是等边三角形,
∴AB=BE=50m.
第1页(共1页)
同课章节目录
