24.3正多边形和圆 强化练习(无答案)2023—2024学年人教版数学九年级上册
文档属性
| 名称 | 24.3正多边形和圆 强化练习(无答案)2023—2024学年人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 282.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-29 15:42:24 | ||
图片预览

文档简介
24.3正多边形和圆 强化练
选择题
1.如图,正五边形的五个内角都相等,五条边都相等,连结对角线AD,BE,CE,线段AD分别与BE和CE相交于点M,N.下列结论:①∠AME=108°;②AN=AE;③∠EBC=2∠BEC,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.0个
2.周长相等的正方形与正六边形的面积分别为S1、S2,S1和S2的关系为( )
A.S1=S2 B.S1:S2=3:16
C.S1:S2=:3 D.S1:S2=:2
3.如图,边长相等的正八边形和正方形部分重叠摆放在一起,已知正方形面积是2,那么非阴影部分面积是( )
A.6 B. C. D.8
4.如图,在正六边形ABCDEF中,M,N分别为边CD,BC的中点,AN与BM相交于点P,则∠APM的度数是( )
A.110° B.120° C.118° D.122°
5.已知是锐角的内切圆,点、、是三个切点,则的形状是( )
钝角三角形 B.直角三角形 C.锐角三角形 D.无法确定
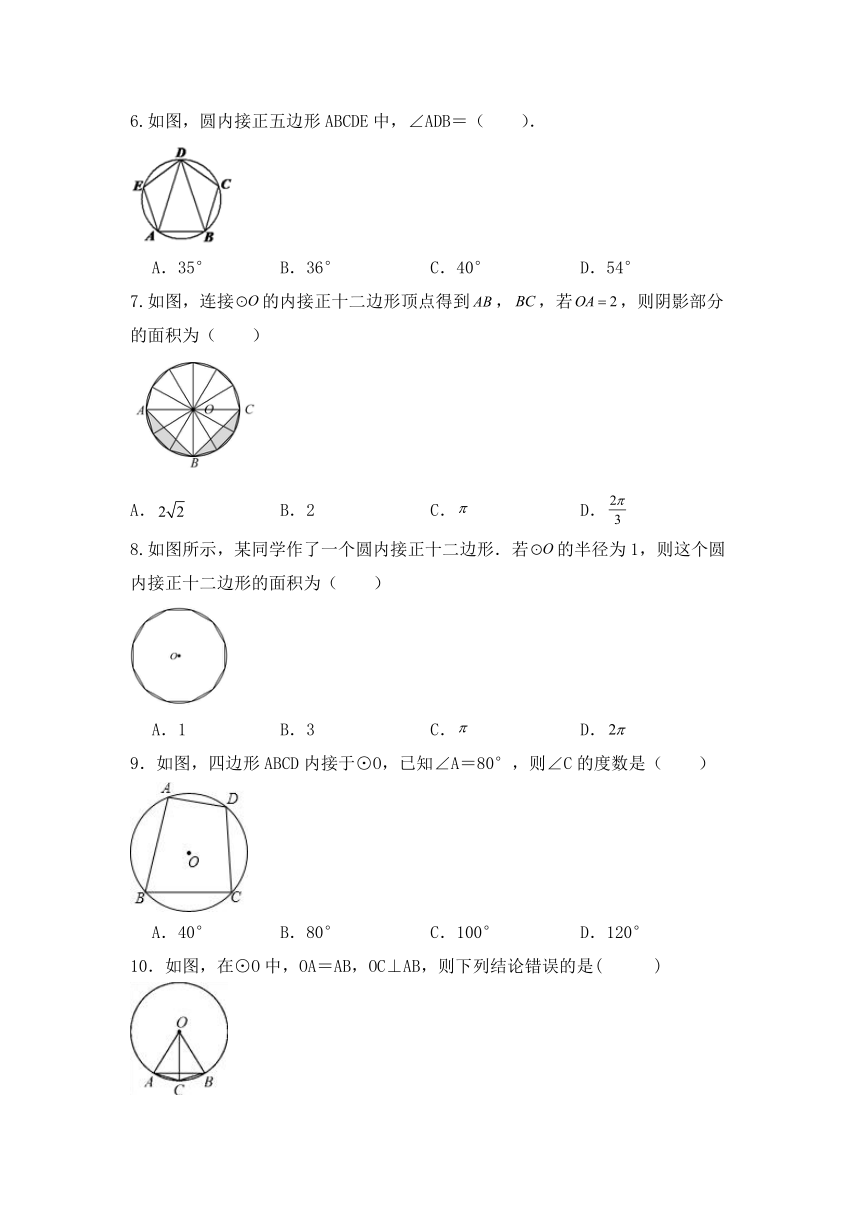
6.如图,圆内接正五边形ABCDE中,∠ADB=( ).
A.35° B.36° C.40° D.54°
7.如图,连接的内接正十二边形顶点得到,,若,则阴影部分的面积为( )
A. B.2 C. D.
8.如图所示,某同学作了一个圆内接正十二边形.若的半径为1,则这个圆内接正十二边形的面积为( )
A.1 B.3 C. D.
9.如图,四边形ABCD内接于⊙O,已知∠A=80°,则∠C的度数是( )
A.40° B.80° C.100° D.120°
10.如图,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是( )
A.△OAB是等边三角形 B.弦AC的长等于圆内接正十二边形的边长
C.OC平分弦AB D.∠BAC=30°
二、填空题
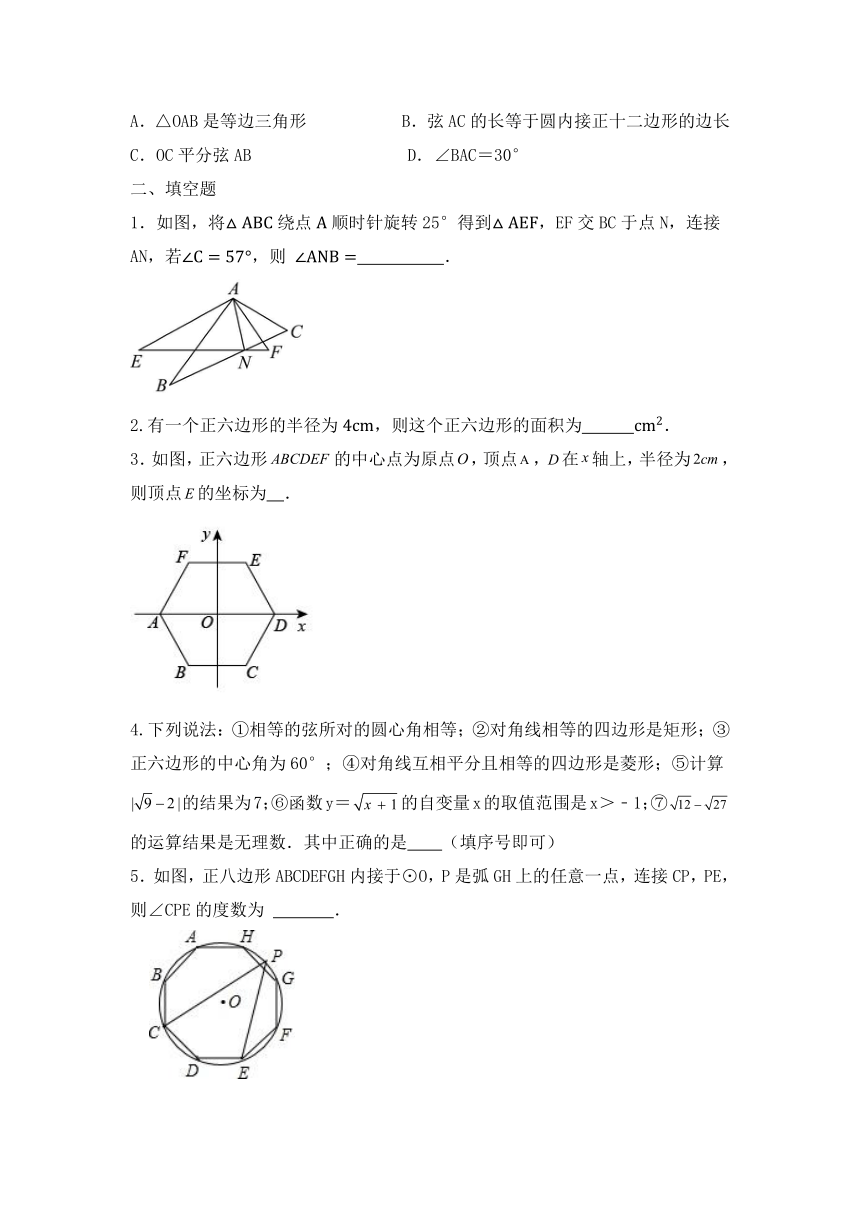
1.如图,将绕点顺时针旋转25°得到,EF交BC于点N,连接AN,若,则 .
2.有一个正六边形的半径为,则这个正六边形的面积为 .
3.如图,正六边形的中心点为原点,顶点,在轴上,半径为,则顶点的坐标为 .
4.下列说法:①相等的弦所对的圆心角相等;②对角线相等的四边形是矩形;③正六边形的中心角为60°;④对角线互相平分且相等的四边形是菱形;⑤计算的结果为7;⑥函数y=的自变量x的取值范围是x>﹣1;⑦的运算结果是无理数.其中正确的是 (填序号即可)
5.如图,正八边形ABCDEFGH内接于⊙O,P是弧GH上的任意一点,连接CP,PE,则∠CPE的度数为 .
6.如图,如果AB、AC分别是圆O的内接正三角形和内接正方形的一条边,BC一定是圆O的内接正n边形的一条边,那么n= .
7.如图,正五边形内接于,点F在劣弧上,则的度数为 °.
8.如图,四边形是的内接正方形,E是的中点,交于点F,则
度.
解答题
1.如图,已知、、是的内接正十边形的边,连接、、,求证:.
2.如图,正六边形内接于,半径为.
(1)求的长度;
(2)若G为的中点,连接,求的长度.
3.如图,正方形ABCD内接于⊙O,P为上的一点,连接DP,CP.
(1)求∠CPD的度数;
(2)当点P为的中点时,CP是⊙O的内接正n边形的一边,求n的值.
4.如图,正六边形ABCDEF中,点M在AB边上,∠FMH=120°,MH与六边形外角的平分线BQ交于点H.
(1)当点M不与点A、B重合时,求证:∠AFM=∠BMH.
(2)当点M在正六边形ABCDEF一边AB上运动(点M不与点B重合)时,猜想FM与MH的数量关系,并对猜想的结果加以证明.
5.定义:有一个角是其对角一半的圆的内接四边形叫做圆美四边形,其中这个角叫做美角.
(1)如图1,若四边形是圆美四边形,则美角______度.
(2)在(1)的条件下,若的半径为10.
①求的长.
②如图2,在四边形中,若平分,求证:.
(3)在(1)的条件下,如图3,若是的直径,用等式直接写出线段,,之间的数量关系.
选择题
1.如图,正五边形的五个内角都相等,五条边都相等,连结对角线AD,BE,CE,线段AD分别与BE和CE相交于点M,N.下列结论:①∠AME=108°;②AN=AE;③∠EBC=2∠BEC,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.0个
2.周长相等的正方形与正六边形的面积分别为S1、S2,S1和S2的关系为( )
A.S1=S2 B.S1:S2=3:16
C.S1:S2=:3 D.S1:S2=:2
3.如图,边长相等的正八边形和正方形部分重叠摆放在一起,已知正方形面积是2,那么非阴影部分面积是( )
A.6 B. C. D.8
4.如图,在正六边形ABCDEF中,M,N分别为边CD,BC的中点,AN与BM相交于点P,则∠APM的度数是( )
A.110° B.120° C.118° D.122°
5.已知是锐角的内切圆,点、、是三个切点,则的形状是( )
钝角三角形 B.直角三角形 C.锐角三角形 D.无法确定
6.如图,圆内接正五边形ABCDE中,∠ADB=( ).
A.35° B.36° C.40° D.54°
7.如图,连接的内接正十二边形顶点得到,,若,则阴影部分的面积为( )
A. B.2 C. D.
8.如图所示,某同学作了一个圆内接正十二边形.若的半径为1,则这个圆内接正十二边形的面积为( )
A.1 B.3 C. D.
9.如图,四边形ABCD内接于⊙O,已知∠A=80°,则∠C的度数是( )
A.40° B.80° C.100° D.120°
10.如图,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是( )
A.△OAB是等边三角形 B.弦AC的长等于圆内接正十二边形的边长
C.OC平分弦AB D.∠BAC=30°
二、填空题
1.如图,将绕点顺时针旋转25°得到,EF交BC于点N,连接AN,若,则 .
2.有一个正六边形的半径为,则这个正六边形的面积为 .
3.如图,正六边形的中心点为原点,顶点,在轴上,半径为,则顶点的坐标为 .
4.下列说法:①相等的弦所对的圆心角相等;②对角线相等的四边形是矩形;③正六边形的中心角为60°;④对角线互相平分且相等的四边形是菱形;⑤计算的结果为7;⑥函数y=的自变量x的取值范围是x>﹣1;⑦的运算结果是无理数.其中正确的是 (填序号即可)
5.如图,正八边形ABCDEFGH内接于⊙O,P是弧GH上的任意一点,连接CP,PE,则∠CPE的度数为 .
6.如图,如果AB、AC分别是圆O的内接正三角形和内接正方形的一条边,BC一定是圆O的内接正n边形的一条边,那么n= .
7.如图,正五边形内接于,点F在劣弧上,则的度数为 °.
8.如图,四边形是的内接正方形,E是的中点,交于点F,则
度.
解答题
1.如图,已知、、是的内接正十边形的边,连接、、,求证:.
2.如图,正六边形内接于,半径为.
(1)求的长度;
(2)若G为的中点,连接,求的长度.
3.如图,正方形ABCD内接于⊙O,P为上的一点,连接DP,CP.
(1)求∠CPD的度数;
(2)当点P为的中点时,CP是⊙O的内接正n边形的一边,求n的值.
4.如图,正六边形ABCDEF中,点M在AB边上,∠FMH=120°,MH与六边形外角的平分线BQ交于点H.
(1)当点M不与点A、B重合时,求证:∠AFM=∠BMH.
(2)当点M在正六边形ABCDEF一边AB上运动(点M不与点B重合)时,猜想FM与MH的数量关系,并对猜想的结果加以证明.
5.定义:有一个角是其对角一半的圆的内接四边形叫做圆美四边形,其中这个角叫做美角.
(1)如图1,若四边形是圆美四边形,则美角______度.
(2)在(1)的条件下,若的半径为10.
①求的长.
②如图2,在四边形中,若平分,求证:.
(3)在(1)的条件下,如图3,若是的直径,用等式直接写出线段,,之间的数量关系.
同课章节目录
