4.1.2 点、线、面、体 提升练习(无答案)2023—2024学年人教版数学七年级上册
文档属性
| 名称 | 4.1.2 点、线、面、体 提升练习(无答案)2023—2024学年人教版数学七年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 389.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-29 00:00:00 | ||
图片预览


文档简介
4.1.2 点、线、面、体 提升练习
一、选择题
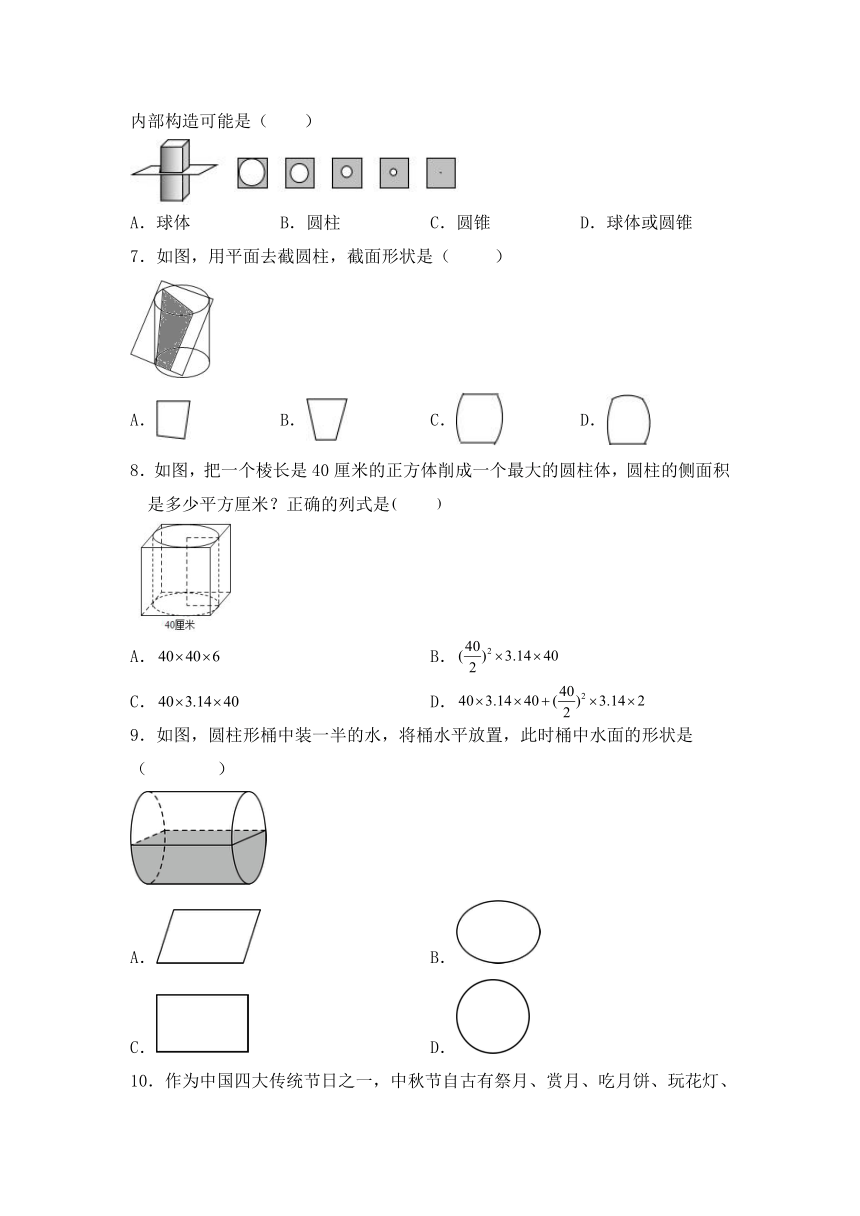
1.下面几何体中,全是由曲面围成的是( )
A.圆柱 B.圆锥 C.球 D.正方体
2.下列几何体中,不完全是由平面围成的是( )
3.下面几何体中,不能由一个平面图形通过旋转得到的是
A. B. C. D.
4.你见过一种折叠灯笼吗?它看起来是平面的,可是提起来后却变成了美丽的灯笼,这个过程可近似地用哪个数学原理来解释( )
A.点动成线 B.线动成面
C.面动成体 D.面与面相交的地方是线
5.如图,几何体的截面形状是( )
A. B. C. D.
6.一个物体的外形是长方体,其内部构造不详.用5个水平的平面纵向平均截这个物体时,得到了一组(自下而上)截面,截面形状如图所示,这个长方体的内部构造可能是( )
A.球体 B.圆柱 C.圆锥 D.球体或圆锥
7.如图,用平面去截圆柱,截面形状是( )
A. B. C. D.
8.如图,把一个棱长是40厘米的正方体削成一个最大的圆柱体,圆柱的侧面积是多少平方厘米?正确的列式是
A. B.
C. D.
9.如图,圆柱形桶中装一半的水,将桶水平放置,此时桶中水面的形状是( )
A. B.
C. D.
10.作为中国四大传统节日之一,中秋节自古有祭月、赏月、吃月饼、玩花灯、赏桂花等民俗.如图所示,某月饼可以看成一个圆柱体,用一个平面去截该圆柱体,则截面不可能是( )
A.三角形 B.椭圆 C.长方形 D.圆
二、填空题
1.航天飞机拖着“长长的火焰”,我们用数学知识可解释为点动成线.用数学知识解释下列现象:
(1)一只小蚂蚁爬行留下的路线可解释为 .
(2)电动车车辐条运动形成的图形可解释为 .
2.如图,正方形ABCD的边长为3 cm,以直线AB为轴,将正方形旋转一周,所得几何体从正面看的图形的面积是 cm2.
3.一个圆柱体,它的底面半径为,高为.用一个平面去截该圆柱体,截得的长方形面积的最大值为 .
4.如图所示,在直角三角形中,绕着以3为直角边所在的直线为轴旋转一周,得到几何体的体积为 .(结果保留π)
5.将一个直角三角形ABC绕它的一边旋转,旋转后所得的几何体可能是下面图中的哪个 .
6.如图,在长方体中,可以把面与面组成的图形看作直立于面上的合页型折纸,从而说明棱 ⊥面.
7.10个棱长为ycm的正方体摆放成如图的形状,则这个图形的表面积为 cm2.
解答题
1.我们知道将一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱.现在有一个长为4cm,宽为3cm的长方形,分别绕它的长、宽所在的直线旋转一周,得到不同的圆柱,它们的体积分别是多少?
2.如图所示,用一个平面去截掉一个正方体的一条棱.
(1)剩下的几何体的形状是什么?
(2)剩下的几何体有几个顶点?几条棱?几个面?
(3)若按此方法截掉一个n棱柱的一条棱,则剩下的几何体有几个顶点?几条棱?几个面?
3.我们知道,三棱柱的上、下底面都是三角形,那么正三棱柱的上、下底面都是等边三角形,如图,大正三棱柱的高为10,截取一个底面周长为3的小正三棱柱.
(1)请写出截面的形状;
(2)请计算截面的面积.
4.如图所示,已知直角三角形纸板ABC,直角边AB=4cm,BC=8cm.
(1)将直角三角形纸板绕三角形的边所在的直线旋转一周,能得到 种大小不同的几何体?
(2)分别计算绕三角形直角边所在的直线旋转一周,得到的几何体的体积?(圆锥的体积=πr2h,其中π取3)
5.如图,某银行大堂的旋转门内部由三块宽为2m、高为3m的玻璃隔板组成.
(1)将此旋转门旋转一周,能形成的几何体是圆柱.这能说明的事实___________(选择正确的一项填入).
A.点动成线 B.线动成面 C.面动成体
(2)求该旋转门旋转一周形成的几何体的体积.(边框及衔接处忽略不计,结果保留)
一、选择题
1.下面几何体中,全是由曲面围成的是( )
A.圆柱 B.圆锥 C.球 D.正方体
2.下列几何体中,不完全是由平面围成的是( )
3.下面几何体中,不能由一个平面图形通过旋转得到的是
A. B. C. D.
4.你见过一种折叠灯笼吗?它看起来是平面的,可是提起来后却变成了美丽的灯笼,这个过程可近似地用哪个数学原理来解释( )
A.点动成线 B.线动成面
C.面动成体 D.面与面相交的地方是线
5.如图,几何体的截面形状是( )
A. B. C. D.
6.一个物体的外形是长方体,其内部构造不详.用5个水平的平面纵向平均截这个物体时,得到了一组(自下而上)截面,截面形状如图所示,这个长方体的内部构造可能是( )
A.球体 B.圆柱 C.圆锥 D.球体或圆锥
7.如图,用平面去截圆柱,截面形状是( )
A. B. C. D.
8.如图,把一个棱长是40厘米的正方体削成一个最大的圆柱体,圆柱的侧面积是多少平方厘米?正确的列式是
A. B.
C. D.
9.如图,圆柱形桶中装一半的水,将桶水平放置,此时桶中水面的形状是( )
A. B.
C. D.
10.作为中国四大传统节日之一,中秋节自古有祭月、赏月、吃月饼、玩花灯、赏桂花等民俗.如图所示,某月饼可以看成一个圆柱体,用一个平面去截该圆柱体,则截面不可能是( )
A.三角形 B.椭圆 C.长方形 D.圆
二、填空题
1.航天飞机拖着“长长的火焰”,我们用数学知识可解释为点动成线.用数学知识解释下列现象:
(1)一只小蚂蚁爬行留下的路线可解释为 .
(2)电动车车辐条运动形成的图形可解释为 .
2.如图,正方形ABCD的边长为3 cm,以直线AB为轴,将正方形旋转一周,所得几何体从正面看的图形的面积是 cm2.
3.一个圆柱体,它的底面半径为,高为.用一个平面去截该圆柱体,截得的长方形面积的最大值为 .
4.如图所示,在直角三角形中,绕着以3为直角边所在的直线为轴旋转一周,得到几何体的体积为 .(结果保留π)
5.将一个直角三角形ABC绕它的一边旋转,旋转后所得的几何体可能是下面图中的哪个 .
6.如图,在长方体中,可以把面与面组成的图形看作直立于面上的合页型折纸,从而说明棱 ⊥面.
7.10个棱长为ycm的正方体摆放成如图的形状,则这个图形的表面积为 cm2.
解答题
1.我们知道将一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱.现在有一个长为4cm,宽为3cm的长方形,分别绕它的长、宽所在的直线旋转一周,得到不同的圆柱,它们的体积分别是多少?
2.如图所示,用一个平面去截掉一个正方体的一条棱.
(1)剩下的几何体的形状是什么?
(2)剩下的几何体有几个顶点?几条棱?几个面?
(3)若按此方法截掉一个n棱柱的一条棱,则剩下的几何体有几个顶点?几条棱?几个面?
3.我们知道,三棱柱的上、下底面都是三角形,那么正三棱柱的上、下底面都是等边三角形,如图,大正三棱柱的高为10,截取一个底面周长为3的小正三棱柱.
(1)请写出截面的形状;
(2)请计算截面的面积.
4.如图所示,已知直角三角形纸板ABC,直角边AB=4cm,BC=8cm.
(1)将直角三角形纸板绕三角形的边所在的直线旋转一周,能得到 种大小不同的几何体?
(2)分别计算绕三角形直角边所在的直线旋转一周,得到的几何体的体积?(圆锥的体积=πr2h,其中π取3)
5.如图,某银行大堂的旋转门内部由三块宽为2m、高为3m的玻璃隔板组成.
(1)将此旋转门旋转一周,能形成的几何体是圆柱.这能说明的事实___________(选择正确的一项填入).
A.点动成线 B.线动成面 C.面动成体
(2)求该旋转门旋转一周形成的几何体的体积.(边框及衔接处忽略不计,结果保留)
