【提分必刷】浙江地区九年级上学期期末数学必刷卷4(浙教版 含解析)
文档属性
| 名称 | 【提分必刷】浙江地区九年级上学期期末数学必刷卷4(浙教版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-29 09:35:15 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【提分必刷】浙江地区九年级上学期期末数学必刷卷4(浙教版)
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,将木条a,b与c钉在一起,∠1=70°,∠2=50°,要使木条a与b平行,木条a旋转的度数至少是( )
A.10° B.20° C.50° D.70°
2.已知,点为线段的黄金分割点,则的长为( )
A. B. C. D.
3.如图,平行四边形ABCD的顶点A、B、D在⊙O上,顶点C在⊙O直径BE上,连结AE,若∠E=36°,则∠ADC的度数是( )
A.44° B.53° C.72° D.54°
4.二次函数图象的顶点坐标是( )
A. B. C. D.
5.从编号为1~10的10个完全相同的球中,任取一球,其号码能被3整除的概率是( )
A. B. C. D.
6.已知二次函数y=x2﹣2x﹣4,当自变量x的取值范围是x≥﹣1时,下列关于函数y的最值说法正确的是( )
A.有最小值﹣5,有最大值﹣1
B.有最小值﹣5,无最大值
C.有最小值﹣1,无最大值
D.无最小值,有最大值﹣1
7.如图,是的弦,于点,若,,则弦的长为( )
A.4 B. C. D.
8.下列函数中,当x>0时,y值随x值增大而减小的是( ).
A.y=x-3 B.y=-3x2 C. D.
二、填空题
9.在半径为5的圆内放置正方形,E为的中点,交圆于点F,直线分别交圆于点G,H,如图所示.若,则的长为 .
10.如图是小明的健康绿码示意图,用黑白打印机打印于边长为的正方形区域内,为了估计图中黑色部分的总面积,经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,则黑色部分的面积为 .
11.如图,有8张标记数字1-8的卡片.甲、乙两人玩一个游戏,规则是:甲、乙两人轮流从中取走卡片;每次可以取1张,也可以取2张,还可以取3张卡片(取2张或3张卡片时,卡片上标记的数字必须连续);最后一个将卡片取完的人获胜.
若甲先取走标记2,3的卡片,乙又取走标记7,8的卡片,接着甲取走两张卡片,则 (填“甲”或“乙”)一定获胜;若甲首次取走标记数字1,2,3的卡片,乙要保证一定获胜,则乙首次取卡片的方案是 .(只填一种方案即可)
12.已知,,是抛物线上的点,则、、的大小关系为 .
13.工程上常用钢珠来测量零件上小孔的直径.假设钢珠的直径是12毫米,测得钢珠顶端离零件表面的距离为9毫米,如图所示,则这个小孔的直径AB是 毫米.
14.将抛物线绕它的顶点旋转后得到的抛物线解析式为 .
三、解答题
15.抛物线与x轴交于点,点,与y轴交于点C,点D是该抛物线的顶点,连接,.
(1)将抛物线化成的形式;
(2)根据题意,画出图象,标出各点;
(3)点P是抛物线上的一动点,若的面积是面积的一半,求点P的坐标.
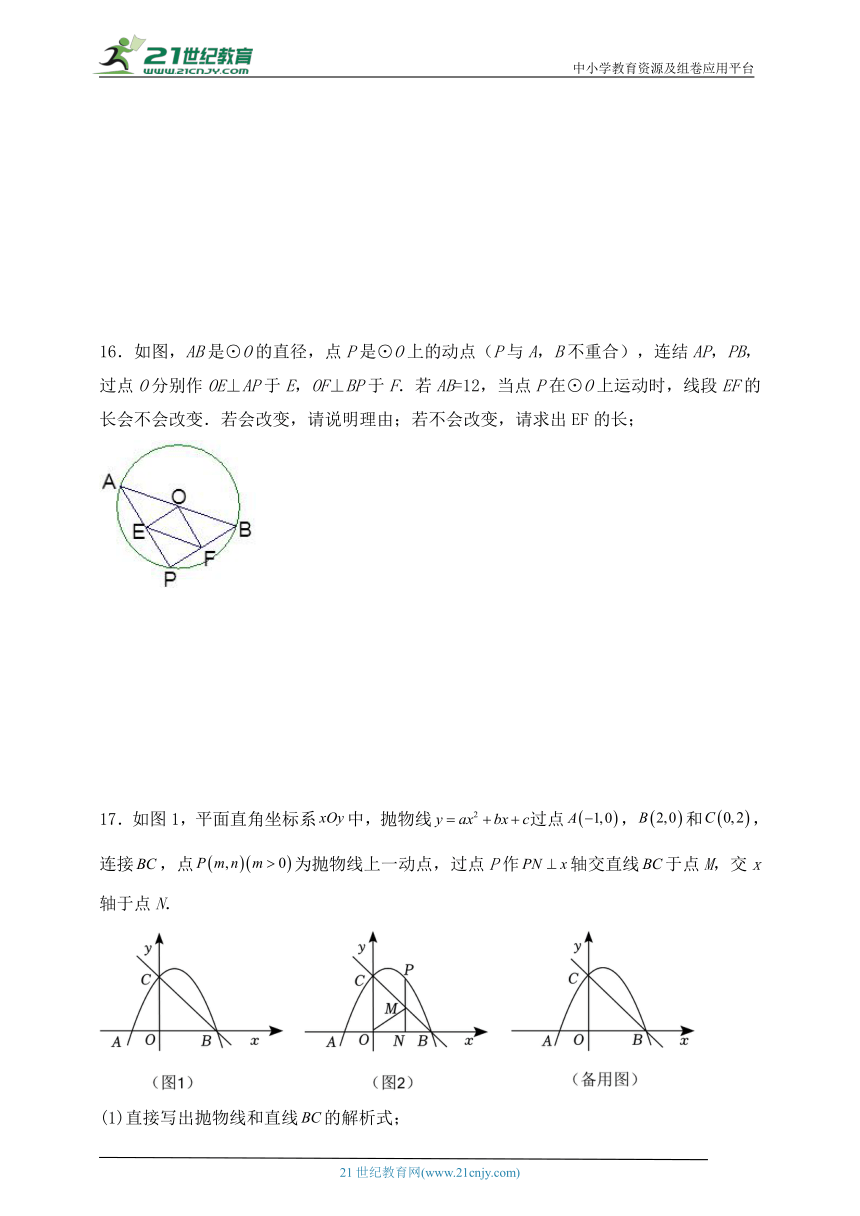
16.如图,AB是⊙O的直径,点P是⊙O上的动点(P与A,B不重合),连结AP,PB,过点O分别作OE⊥AP于E,OF⊥BP于F.若AB=12,当点P在⊙O上运动时,线段EF的长会不会改变.若会改变,请说明理由;若不会改变,请求出EF的长;
17.如图1,平面直角坐标系中,抛物线过点,和,连接,点为抛物线上一动点,过点P作轴交直线于点M,交x轴于点N.
(1)直接写出抛物线和直线的解析式;
(2)如图2,连接,当为等腰三角形时,求m的值;
(3)是否存在点这样的点P,使得以O,M,N为顶点的三角形与以O,A,C为顶点的三角形相似,若存在,直接写出点P的坐标;若不存在,请说明理由.
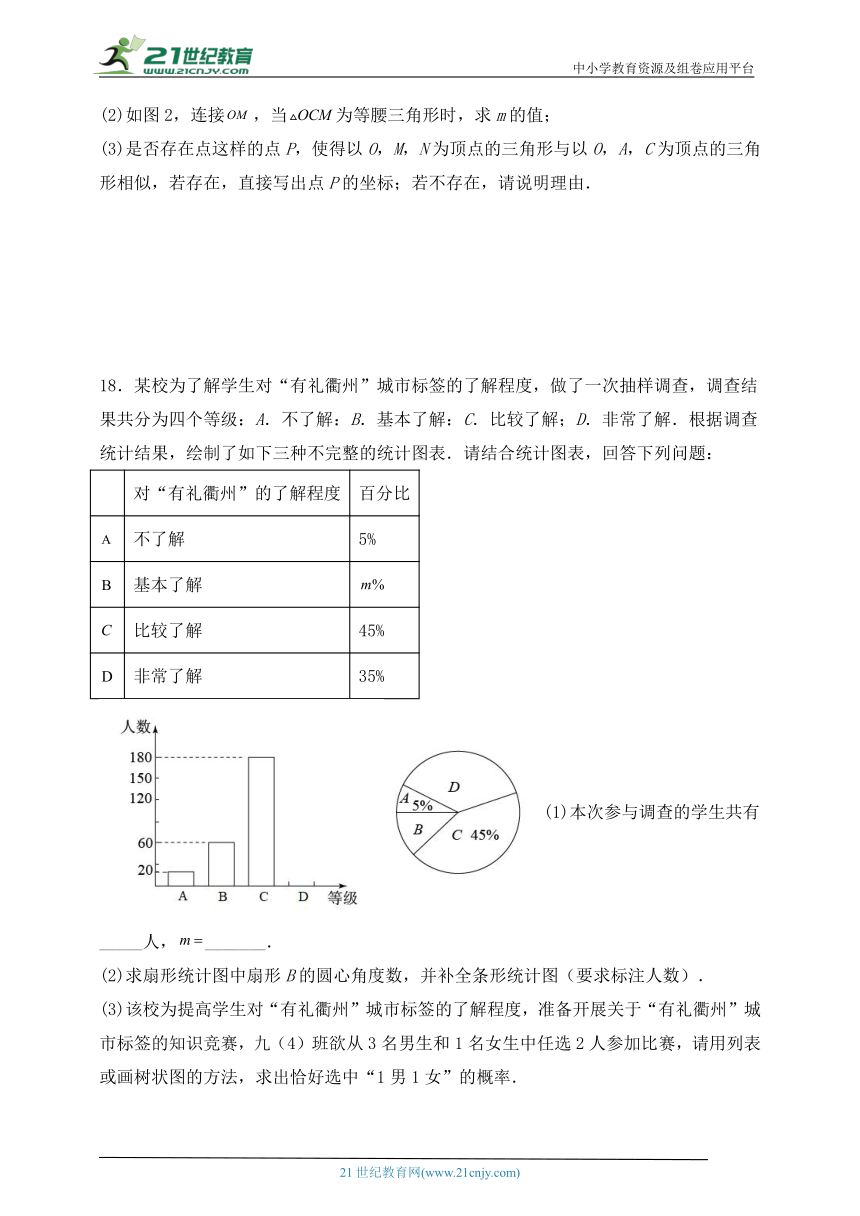
18.某校为了解学生对“有礼衢州”城市标签的了解程度,做了一次抽样调查,调查结果共分为四个等级:A.不了解:B.基本了解:C.比较了解;D.非常了解.根据调查统计结果,绘制了如下三种不完整的统计图表.请结合统计图表,回答下列问题:
对“有礼衢州”的了解程度 百分比
不了解 5%
基本了解
比较了解 45%
非常了解 35%
(1)本次参与调查的学生共有_____人,_______.
(2)求扇形统计图中扇形B的圆心角度数,并补全条形统计图(要求标注人数).
(3)该校为提高学生对“有礼衢州”城市标签的了解程度,准备开展关于“有礼衢州”城市标签的知识竞赛,九(4)班欲从3名男生和1名女生中任选2人参加比赛,请用列表或画树状图的方法,求出恰好选中“1男1女”的概率.
19.根据题意,解决下列问题.
(1)已知是等边三角形的外接圆,的半径为r,等边三角形边长为a,求r与a的比值;
(2)已知是等腰三角形的外接圆,D,E分别是的中点,,,求O到的距离;
(3)已知是等腰三角形的外接圆,D,E分别是的中点,直线交于F,G,且D,E是线段的三等分点;
①若,求的值;
②与的比值是否为定值,若是请直接写出答案,若不是请说明理由.
20.已知抛物线的顶点坐标为,且经过轴上一点.
(1)求抛物线解析式;
(2)求抛物线与轴的交点坐标;
(3)试说明:当时,函数值随着的增大而变化的情况.
21.小明和爸爸玩“石头”、“剪刀”、 “剪刀”的游戏,游戏规则:每局游戏每人用一只手可以出石头、 剪刀、布三种手势中的一种;石头赢剪刀,剪刀赢布,布赢石头;若两人出相同手势,则算平局.
(1)在一局游戏中,小明决定出“剪刀”,求他赢爸爸的概率;
(2)用列举法求一局游戏中两人出现平局的概率.
22.如图,的三个顶点的坐标分别为、、.
(1)将以点C为旋转中心旋转,画出旋转后对应的;
(2)平移,若A对应点的坐标为,画出平移后对应的;
(3)若将绕某一点旋转得到,请直接写出旋转中心的坐标为
参考答案:
1.B
【分析】要使木条a与b平行,那么∠1=∠2,从而可求出木条a至少旋转的度数.
【详解】解:∵要使木条a与b平行,
∴∠1=∠2,
∴当∠1需变为50 ,
∴木条a至少旋转:70 -50 =20 .
故选B.
【点睛】本题考查了旋转的性质及平行线的性质:①两直线平行同位角相等;②两直线平行内错角相等;③两直线平行同旁内角互补;④夹在两平行线间的平行线段相等.在运用平行线的性质定理时,一定要找准同位角,内错角和同旁内角.
2.A
【分析】根据黄金分割点的定义,代入数据即可得出的长.
【详解】解:由于为线段的黄金分割点,
且是较长线段;
则,
故选:A.
【点睛】本题考查了黄金分割的概念:把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割.
3.D
【分析】根据直径所对的圆周角为直角可得∠BAE=90°,再根据直角三角形的性质和平行四边形的性质可得解.
【详解】根据直径所对的圆周角为直角可得∠BAE=90°,
根据∠E=36°可得∠B=54°,
根据平行四边形的性质可得∠ADC=∠B=54°.
故选D
【点睛】本题考查了平行四边形的性质、圆的基本性质.
4.C
【分析】利用二次函数的性质解答.
【详解】解:二次函数,
二次函数图象的顶点坐标为.
故选:C.
【点睛】本题考查二次函数的性质,解答本题的关键是明确题意,利用二次函数的性质解答.
5.C
【分析】根据数的整除性得出连续自然数每10个有三个能整除3,即可得出卡片号能被3整除的概率.
【详解】解:∵10张已编号的球(编号为连续的自然数)有三个能整除3,为3,6,9,
∴号码能被3整除的概率为.
故选C.
【点睛】此题考查了概率公式,用到的知识点为:概率=所求情况数与总情况数之比.
6.B
【分析】函数图象开口向上,由函数解析式求出顶点的坐标,再结合x≥﹣1进行分析即可.
【详解】∵
∴二次函数图象开口向上
∵
∴函数顶点坐标为,即对称轴为
∵x≥﹣1
∴当时y随x的增大而减小,当时y随x的增大而增大
∴二次函数在顶点出取最小值,最小值-5,没有最大值
故选:B.
【点睛】本题考查二次函数的性质,时,对称轴左边y随x的增大而减小,对称轴右边y随x的增大而增大.
7.D
【分析】根据含30度角的直角三角形的性质,勾股定理可得,根据垂径定理可得,即可得出答案.
【详解】解:∵,
∴,
∵,,
∴,
∴,
∴,
∴,
故选:D.
【点睛】本题考查了根据垂径定理求值,含30度角的直角三角形的性质,勾股定理,难度不大.
8.B
【详解】试题分析:A.y=x-3中,y随x的增大而增大;B. y=-3x2中,当x<0时,y随x的增大而增大,当x>0时,y随x的增大而减小;C.中,y随x的增大而增大;D.中,在每一象限内,y随x的增大而增大.
故选B.
考点:一次函数的增减性;二次函数的增减性;反比例函数的增减性.
9.
【分析】根据正方形的性质推出,根据相似三角形的性质得出,根据线段的和差求解即可.
【详解】解:∵四边形是正方形,
∴,
∴,
∵ ,
∴,
∴,
∴,
∴,
∵,E为的中点,
∴,
∴,
∴,
∵,
∴,
∴或(舍去),
∴,
∴,
故答案为:.
【点睛】本题考查正方形的性质,以及相似三角形的判定和性质.熟练掌握正方形的性质,判定三角形相似是解题的关键.
10.2.4
【分析】经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,可得点落入黑色部分的概率为0.6,根据边长为的正方形的面积为,进而可以估计黑色部分的总面积.
【详解】解:∵经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,
∴点落入黑色部分的概率为0.6,
∵边长为的正方形的面积为,
设黑色部分的面积为S,
则,
解得.
∴估计黑色部分的总面积约为.
故答案为:2.4.
【点睛】本题考查了利用频率估计概率,解决本题的关键是掌握概率公式,知道点落入黑色部分的概率为0.6.
11. 甲 取走标记5,6,7的卡片(答案不唯一)
【分析】由游戏规则分析判断即可作出结论.
【详解】解:若甲先取走标记2,3的卡片,乙又取走标记7,8的卡片,接着甲取走两张卡片,为4,5或5,6,则剩余的卡片为1,6或1,4,然后乙只能取走一张卡片,最后甲将一张卡片取完,则甲一定获胜;
若甲首次取走标记数字1,2,3的卡片,乙要保证一定获胜,则乙首次取卡片的方案5,6,7,理由如下:
乙取走5,6,7,则甲再取走4和8中的一个,最后乙取走剩下的一个,则乙一定获胜,
故答案为:甲;5,6,7(答案不唯一).
【点睛】本题考查游戏公平性,理解游戏规则是解答的关键.
12./
【分析】求出抛物线的对称轴为直线,然后根据二次函数的增减性解答即可.
【详解】解:∵,
∴抛物线的对称轴为直线,
∵,
∴抛物线开口向下,
∴当时,y随x的增大而增大,当时,函数有最大值,
∵关于对称点为,,
∴.
故答案为:.
【点睛】本题考查了二次函数图象上点的坐标特征,熟练求出对称轴,并熟悉二次函数的增减性是解题的关键.
13.6
【分析】设钢珠的圆心为O,过O作OC⊥AB于C,交优弧AB于D,连OC,则OA=12÷2=6mm,CD=9mm,OC=9mm-6mm=3mm,根据垂径定理得到CA=CB,在Rt△AOC中,利用勾股定理可计算出AC,即可得到这个小孔的直径AB.
【详解】解:如图,
设钢珠的圆心为O,过O作OC⊥AB于C,交优弧AB于D,连OC,
则OA=12÷2=6mm,CD=9mm,OC=9mm 6mm=3mm,
∵OC⊥AB,
∴CA=CB,
在Rt△AOC中,AC=(mm).
∴AB=2AC=mm.
所以这个小孔的直径AB是毫米.
故答案为.
14.
【分析】根据题意将抛物线绕顶点坐标旋转后,顶点坐标不变,开口方向相反,开口大小不变,据此解答即可.
【详解】解:∵抛物线绕它的顶点旋转,
∴顶点坐标仍为,开口大小不变,即,开口方向相反,即,
∴旋转后的解析式为.
故答案为:.
【点睛】本题考查了二次函数的性质,根据题意得出旋转后顶点坐标不变,开口方向相反,开口大小不变是解本题的关键.
15.(1)
(2)见解析
(3)点P的坐标为点P的坐标为或或或
【分析】(1)利用配方法进行转化即可;
(2)根据五点作图法进行作图即可;
(3)利用进行计算即可.
【详解】(1)解:,
,
;
(2)解:由(1)知顶点,对称轴为直线,
∵,
∴C的对称点为,
又∵与x轴交于点,点,
根据五点法作图如下:
(3)解:∵点,点,
∴,
∴;
∵的面积是面积的一半,
∴,
∵,
∴P点纵坐标为2或,
当P点纵坐标为2,则,
解得:,
此时P点坐标为: 或,
当P点纵坐标为,则,
解得:,
此时P点坐标为:或,
综上所述:点P的坐标为或或或.
【点睛】本题考查二次函数的综合应用,熟练掌握二次函数的图像和性质是解题的关键.
16.不变,6
【详解】试题分析:由于OE、OF都经过圆心,且垂直于AP、BP,由垂径定理知E、F分别是AP、PB的中点,即EF是△APB的中位线,由此可得到EF==6,因此EF的长不会改变.
试题解析:EF的长不会改变.
∵OE⊥AP于E,OF⊥BP于F,
∴AE=EP,BF=FP,
∴EF=AB=6
17.(1),
(2)或或
(3)存在,点的坐标为或或
【分析】(1)利用待定系数法求出即可得;
(2)先根据直线的解析式求出点的坐标,再利用两点之间的距离公式分别求出,和的值,然后分三种情况:①,②,③,建立方程,解方程即可得;
(3)先分别求出的值,再分两种情况:①和②,利用相似三角形的性质求解即可得.
【详解】(1)解:将点代入得:,
解得,
则抛物线的解析式为;
设直线的解析式为,
将点代入得:,解得,
则直线的解析式为.
(2)解:,轴交直线于点,交轴于点,
,
,
,,,
①当时,为等腰三角形,
则,即,
解得或(不符合题意,舍去);
②当时,为等腰三角形,
则,即,
解得或(不符合题意,舍去);
③当时,为等腰三角形,
则,即,
解得,
综上,或或.
(3)解:,
,
①当时,
则,即,
解得或(不符合题意,舍去),
将代入得:,
则此时点的坐标为;
②当时,
则,即,
解得或,
将代入得:,
将代入得:,
则此时点的坐标为或;
综上,存在这样的点,此时点的坐标为或或.
【点睛】本题考查了二次函数的几何应用、一次函数的几何应用、相似三角形的性质、等腰三角形等知识点,较难的是题(3),正确分情况讨论是解题关键.
18.(1)400,15
(2)54°,图见解析
(3)
【分析】(1)根据的人数以及百分比即可求得总人数,根据统计表即可求得的值;
(2)根据的百分比乘以360°即可求解,根据D的百分比求得人数,然后补全统计图即可;
(3)根据列表法求概率即可求解.
【详解】(1)本次参与调查的学生共有(人),
;
(2)扇形统计图中扇形B的圆心角度数为,
人数为140,条形统计图如图;
(3)列表如图,用A表示男生,B表示女生,
A1 A2 A3 B
A1 A1A2 A1A3 A1B
A2 A2A1 A2A3 A2B
A3 A3A1 A3A2 A3B
B BA1 BA2 BA3
所以,恰好选中“1男1女”的概率为.
【点睛】本题考查的是条形统计图和扇形统计图的综合运用,列表法求概率,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
19.(1)
(2)
(3)①;②为定值,,理由见解析
【分析】(1)如图所示,过点O作于D,连接,理由等边三角形的性质和圆周角定理以及垂径定理求出,,再根据勾股定理和含30度角的直角三角形的性质得到,据此求解即可;
(2)如图所示,延长交于F,连接,根据三角形中位线定理得到,再证明,,则,理由勾股定理求出,设,则,在中,,即可求出,在中,;
(3)①如图所示,如图所示,连接, 同理可得,由D,E是线段的三等分点,得到,证明,得到,则;②由,得到,再由,,得到,即可证明,则.
【详解】(1)解:如图所示,过点O作于D,连接,
∵是等边三角形,
∴,
∴,
∵,
∴,,
∴,
∴,
∴,
∴,
∴;
(2)解:如图所示,延长交于F,连接,
∵D,E分别是的中点,
∴是的中位线,
∴,,
∵点O是等腰三角形的外接圆圆心,
∴,,
∴,
∴,
设,则,
在中,,
∴,
∴,
在中,;
(3)解:①如图所示,如图所示,连接,
同理可得,
∵D,E是线段的三等分点,
∴,
∵,
∴,
∴,
∵D是的中点,
∴,
∴,
∴;
②,理由如下:
由①得,
∴,
∵D是的中点,
∴,
∴,
∵D,E是线段的三等分点,
∴,,
∴,
∵,
∴,
∴.
【点睛】本题主要考查了垂径定理,勾股定理,圆周角定理,三角形外接圆,相似三角形的性质与判定,三角形中位线定理等等,灵活运用所学知识是解题的关键.
20.(1)抛物线的解析式为
(2)抛物线与轴的交点坐标为
(3)时,函数值随着的增大而减小
【分析】(1)设顶点式,然后把代入求出的值即可;
(2)计算自变量的值为所对应的函数值即可;
(3)根据二次函数的性质解决问题.
【详解】(1)设抛物线的解析式为,
把代入得,
解得,
抛物线的解析式为;
(2)当时,,
抛物线与轴的交点坐标为;
(3)抛物线的对称轴为直线,抛物线开口向下,
当时,函数值随着的增大而减小.
【点睛】本题考查了待定系数法求二次函数的解析式;解题的关键是在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解,数量掌握二次函数的性质.
21.(1);
(2)
【分析】(1)直接由概率公式求解即可;
(2)用列表法列举出9种可能结果,其中一局游戏中两人出现平局的结果有3种,再由概率公式求解.
【详解】(1)解:在一局游戏中,小明决定出“剪刀”, 他赢爸爸的概率是;
(2)解:列表如下:
石头 剪刀 布
石头 (石头,石头) (石头,剪刀) (石头,布)
剪刀 (剪刀,石头) (剪刀,剪刀) (剪刀,布)
布 (布,石头) (布,剪刀) (布,布)
总共有9种可能,其中一局游戏中出现平局的有3种(剪刀,剪刀)(石头,石头)(布,布),
所以一局游戏中两人出现平局的概率为P=.
【点睛】本题考查了列表法求概率,概率=所求情况数÷总情况数,数据概率公式是解题的关键.
22.(1)见解析
(2)见解析
(3)
【分析】(1)根据网格结构找出点A、B绕点C旋转后的对应点、的位置,然后顺次连接即可;
(2)根据A对应点的坐标为,得出先向右平移3个单位再向下平移6个单位到,找出平移后的对应点、、的位置,然后顺次连接即可;
(3)根据旋转的定义结合图形,连接两对对应点,交点即为旋转中心.
【详解】(1)解:即为所求作的三角形,如图所示:
(2)解:即为所求,如图所示:
(3)解:如图,旋转中心P为;
故答案为:.
【点睛】本题主要考查平移作图和旋转作图,解题的关键是作出平移或旋转后对应点的位置
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【提分必刷】浙江地区九年级上学期期末数学必刷卷4(浙教版)
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,将木条a,b与c钉在一起,∠1=70°,∠2=50°,要使木条a与b平行,木条a旋转的度数至少是( )
A.10° B.20° C.50° D.70°
2.已知,点为线段的黄金分割点,则的长为( )
A. B. C. D.
3.如图,平行四边形ABCD的顶点A、B、D在⊙O上,顶点C在⊙O直径BE上,连结AE,若∠E=36°,则∠ADC的度数是( )
A.44° B.53° C.72° D.54°
4.二次函数图象的顶点坐标是( )
A. B. C. D.
5.从编号为1~10的10个完全相同的球中,任取一球,其号码能被3整除的概率是( )
A. B. C. D.
6.已知二次函数y=x2﹣2x﹣4,当自变量x的取值范围是x≥﹣1时,下列关于函数y的最值说法正确的是( )
A.有最小值﹣5,有最大值﹣1
B.有最小值﹣5,无最大值
C.有最小值﹣1,无最大值
D.无最小值,有最大值﹣1
7.如图,是的弦,于点,若,,则弦的长为( )
A.4 B. C. D.
8.下列函数中,当x>0时,y值随x值增大而减小的是( ).
A.y=x-3 B.y=-3x2 C. D.
二、填空题
9.在半径为5的圆内放置正方形,E为的中点,交圆于点F,直线分别交圆于点G,H,如图所示.若,则的长为 .
10.如图是小明的健康绿码示意图,用黑白打印机打印于边长为的正方形区域内,为了估计图中黑色部分的总面积,经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,则黑色部分的面积为 .
11.如图,有8张标记数字1-8的卡片.甲、乙两人玩一个游戏,规则是:甲、乙两人轮流从中取走卡片;每次可以取1张,也可以取2张,还可以取3张卡片(取2张或3张卡片时,卡片上标记的数字必须连续);最后一个将卡片取完的人获胜.
若甲先取走标记2,3的卡片,乙又取走标记7,8的卡片,接着甲取走两张卡片,则 (填“甲”或“乙”)一定获胜;若甲首次取走标记数字1,2,3的卡片,乙要保证一定获胜,则乙首次取卡片的方案是 .(只填一种方案即可)
12.已知,,是抛物线上的点,则、、的大小关系为 .
13.工程上常用钢珠来测量零件上小孔的直径.假设钢珠的直径是12毫米,测得钢珠顶端离零件表面的距离为9毫米,如图所示,则这个小孔的直径AB是 毫米.
14.将抛物线绕它的顶点旋转后得到的抛物线解析式为 .
三、解答题
15.抛物线与x轴交于点,点,与y轴交于点C,点D是该抛物线的顶点,连接,.
(1)将抛物线化成的形式;
(2)根据题意,画出图象,标出各点;
(3)点P是抛物线上的一动点,若的面积是面积的一半,求点P的坐标.
16.如图,AB是⊙O的直径,点P是⊙O上的动点(P与A,B不重合),连结AP,PB,过点O分别作OE⊥AP于E,OF⊥BP于F.若AB=12,当点P在⊙O上运动时,线段EF的长会不会改变.若会改变,请说明理由;若不会改变,请求出EF的长;
17.如图1,平面直角坐标系中,抛物线过点,和,连接,点为抛物线上一动点,过点P作轴交直线于点M,交x轴于点N.
(1)直接写出抛物线和直线的解析式;
(2)如图2,连接,当为等腰三角形时,求m的值;
(3)是否存在点这样的点P,使得以O,M,N为顶点的三角形与以O,A,C为顶点的三角形相似,若存在,直接写出点P的坐标;若不存在,请说明理由.
18.某校为了解学生对“有礼衢州”城市标签的了解程度,做了一次抽样调查,调查结果共分为四个等级:A.不了解:B.基本了解:C.比较了解;D.非常了解.根据调查统计结果,绘制了如下三种不完整的统计图表.请结合统计图表,回答下列问题:
对“有礼衢州”的了解程度 百分比
不了解 5%
基本了解
比较了解 45%
非常了解 35%
(1)本次参与调查的学生共有_____人,_______.
(2)求扇形统计图中扇形B的圆心角度数,并补全条形统计图(要求标注人数).
(3)该校为提高学生对“有礼衢州”城市标签的了解程度,准备开展关于“有礼衢州”城市标签的知识竞赛,九(4)班欲从3名男生和1名女生中任选2人参加比赛,请用列表或画树状图的方法,求出恰好选中“1男1女”的概率.
19.根据题意,解决下列问题.
(1)已知是等边三角形的外接圆,的半径为r,等边三角形边长为a,求r与a的比值;
(2)已知是等腰三角形的外接圆,D,E分别是的中点,,,求O到的距离;
(3)已知是等腰三角形的外接圆,D,E分别是的中点,直线交于F,G,且D,E是线段的三等分点;
①若,求的值;
②与的比值是否为定值,若是请直接写出答案,若不是请说明理由.
20.已知抛物线的顶点坐标为,且经过轴上一点.
(1)求抛物线解析式;
(2)求抛物线与轴的交点坐标;
(3)试说明:当时,函数值随着的增大而变化的情况.
21.小明和爸爸玩“石头”、“剪刀”、 “剪刀”的游戏,游戏规则:每局游戏每人用一只手可以出石头、 剪刀、布三种手势中的一种;石头赢剪刀,剪刀赢布,布赢石头;若两人出相同手势,则算平局.
(1)在一局游戏中,小明决定出“剪刀”,求他赢爸爸的概率;
(2)用列举法求一局游戏中两人出现平局的概率.
22.如图,的三个顶点的坐标分别为、、.
(1)将以点C为旋转中心旋转,画出旋转后对应的;
(2)平移,若A对应点的坐标为,画出平移后对应的;
(3)若将绕某一点旋转得到,请直接写出旋转中心的坐标为
参考答案:
1.B
【分析】要使木条a与b平行,那么∠1=∠2,从而可求出木条a至少旋转的度数.
【详解】解:∵要使木条a与b平行,
∴∠1=∠2,
∴当∠1需变为50 ,
∴木条a至少旋转:70 -50 =20 .
故选B.
【点睛】本题考查了旋转的性质及平行线的性质:①两直线平行同位角相等;②两直线平行内错角相等;③两直线平行同旁内角互补;④夹在两平行线间的平行线段相等.在运用平行线的性质定理时,一定要找准同位角,内错角和同旁内角.
2.A
【分析】根据黄金分割点的定义,代入数据即可得出的长.
【详解】解:由于为线段的黄金分割点,
且是较长线段;
则,
故选:A.
【点睛】本题考查了黄金分割的概念:把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割.
3.D
【分析】根据直径所对的圆周角为直角可得∠BAE=90°,再根据直角三角形的性质和平行四边形的性质可得解.
【详解】根据直径所对的圆周角为直角可得∠BAE=90°,
根据∠E=36°可得∠B=54°,
根据平行四边形的性质可得∠ADC=∠B=54°.
故选D
【点睛】本题考查了平行四边形的性质、圆的基本性质.
4.C
【分析】利用二次函数的性质解答.
【详解】解:二次函数,
二次函数图象的顶点坐标为.
故选:C.
【点睛】本题考查二次函数的性质,解答本题的关键是明确题意,利用二次函数的性质解答.
5.C
【分析】根据数的整除性得出连续自然数每10个有三个能整除3,即可得出卡片号能被3整除的概率.
【详解】解:∵10张已编号的球(编号为连续的自然数)有三个能整除3,为3,6,9,
∴号码能被3整除的概率为.
故选C.
【点睛】此题考查了概率公式,用到的知识点为:概率=所求情况数与总情况数之比.
6.B
【分析】函数图象开口向上,由函数解析式求出顶点的坐标,再结合x≥﹣1进行分析即可.
【详解】∵
∴二次函数图象开口向上
∵
∴函数顶点坐标为,即对称轴为
∵x≥﹣1
∴当时y随x的增大而减小,当时y随x的增大而增大
∴二次函数在顶点出取最小值,最小值-5,没有最大值
故选:B.
【点睛】本题考查二次函数的性质,时,对称轴左边y随x的增大而减小,对称轴右边y随x的增大而增大.
7.D
【分析】根据含30度角的直角三角形的性质,勾股定理可得,根据垂径定理可得,即可得出答案.
【详解】解:∵,
∴,
∵,,
∴,
∴,
∴,
∴,
故选:D.
【点睛】本题考查了根据垂径定理求值,含30度角的直角三角形的性质,勾股定理,难度不大.
8.B
【详解】试题分析:A.y=x-3中,y随x的增大而增大;B. y=-3x2中,当x<0时,y随x的增大而增大,当x>0时,y随x的增大而减小;C.中,y随x的增大而增大;D.中,在每一象限内,y随x的增大而增大.
故选B.
考点:一次函数的增减性;二次函数的增减性;反比例函数的增减性.
9.
【分析】根据正方形的性质推出,根据相似三角形的性质得出,根据线段的和差求解即可.
【详解】解:∵四边形是正方形,
∴,
∴,
∵ ,
∴,
∴,
∴,
∴,
∵,E为的中点,
∴,
∴,
∴,
∵,
∴,
∴或(舍去),
∴,
∴,
故答案为:.
【点睛】本题考查正方形的性质,以及相似三角形的判定和性质.熟练掌握正方形的性质,判定三角形相似是解题的关键.
10.2.4
【分析】经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,可得点落入黑色部分的概率为0.6,根据边长为的正方形的面积为,进而可以估计黑色部分的总面积.
【详解】解:∵经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,
∴点落入黑色部分的概率为0.6,
∵边长为的正方形的面积为,
设黑色部分的面积为S,
则,
解得.
∴估计黑色部分的总面积约为.
故答案为:2.4.
【点睛】本题考查了利用频率估计概率,解决本题的关键是掌握概率公式,知道点落入黑色部分的概率为0.6.
11. 甲 取走标记5,6,7的卡片(答案不唯一)
【分析】由游戏规则分析判断即可作出结论.
【详解】解:若甲先取走标记2,3的卡片,乙又取走标记7,8的卡片,接着甲取走两张卡片,为4,5或5,6,则剩余的卡片为1,6或1,4,然后乙只能取走一张卡片,最后甲将一张卡片取完,则甲一定获胜;
若甲首次取走标记数字1,2,3的卡片,乙要保证一定获胜,则乙首次取卡片的方案5,6,7,理由如下:
乙取走5,6,7,则甲再取走4和8中的一个,最后乙取走剩下的一个,则乙一定获胜,
故答案为:甲;5,6,7(答案不唯一).
【点睛】本题考查游戏公平性,理解游戏规则是解答的关键.
12./
【分析】求出抛物线的对称轴为直线,然后根据二次函数的增减性解答即可.
【详解】解:∵,
∴抛物线的对称轴为直线,
∵,
∴抛物线开口向下,
∴当时,y随x的增大而增大,当时,函数有最大值,
∵关于对称点为,,
∴.
故答案为:.
【点睛】本题考查了二次函数图象上点的坐标特征,熟练求出对称轴,并熟悉二次函数的增减性是解题的关键.
13.6
【分析】设钢珠的圆心为O,过O作OC⊥AB于C,交优弧AB于D,连OC,则OA=12÷2=6mm,CD=9mm,OC=9mm-6mm=3mm,根据垂径定理得到CA=CB,在Rt△AOC中,利用勾股定理可计算出AC,即可得到这个小孔的直径AB.
【详解】解:如图,
设钢珠的圆心为O,过O作OC⊥AB于C,交优弧AB于D,连OC,
则OA=12÷2=6mm,CD=9mm,OC=9mm 6mm=3mm,
∵OC⊥AB,
∴CA=CB,
在Rt△AOC中,AC=(mm).
∴AB=2AC=mm.
所以这个小孔的直径AB是毫米.
故答案为.
14.
【分析】根据题意将抛物线绕顶点坐标旋转后,顶点坐标不变,开口方向相反,开口大小不变,据此解答即可.
【详解】解:∵抛物线绕它的顶点旋转,
∴顶点坐标仍为,开口大小不变,即,开口方向相反,即,
∴旋转后的解析式为.
故答案为:.
【点睛】本题考查了二次函数的性质,根据题意得出旋转后顶点坐标不变,开口方向相反,开口大小不变是解本题的关键.
15.(1)
(2)见解析
(3)点P的坐标为点P的坐标为或或或
【分析】(1)利用配方法进行转化即可;
(2)根据五点作图法进行作图即可;
(3)利用进行计算即可.
【详解】(1)解:,
,
;
(2)解:由(1)知顶点,对称轴为直线,
∵,
∴C的对称点为,
又∵与x轴交于点,点,
根据五点法作图如下:
(3)解:∵点,点,
∴,
∴;
∵的面积是面积的一半,
∴,
∵,
∴P点纵坐标为2或,
当P点纵坐标为2,则,
解得:,
此时P点坐标为: 或,
当P点纵坐标为,则,
解得:,
此时P点坐标为:或,
综上所述:点P的坐标为或或或.
【点睛】本题考查二次函数的综合应用,熟练掌握二次函数的图像和性质是解题的关键.
16.不变,6
【详解】试题分析:由于OE、OF都经过圆心,且垂直于AP、BP,由垂径定理知E、F分别是AP、PB的中点,即EF是△APB的中位线,由此可得到EF==6,因此EF的长不会改变.
试题解析:EF的长不会改变.
∵OE⊥AP于E,OF⊥BP于F,
∴AE=EP,BF=FP,
∴EF=AB=6
17.(1),
(2)或或
(3)存在,点的坐标为或或
【分析】(1)利用待定系数法求出即可得;
(2)先根据直线的解析式求出点的坐标,再利用两点之间的距离公式分别求出,和的值,然后分三种情况:①,②,③,建立方程,解方程即可得;
(3)先分别求出的值,再分两种情况:①和②,利用相似三角形的性质求解即可得.
【详解】(1)解:将点代入得:,
解得,
则抛物线的解析式为;
设直线的解析式为,
将点代入得:,解得,
则直线的解析式为.
(2)解:,轴交直线于点,交轴于点,
,
,
,,,
①当时,为等腰三角形,
则,即,
解得或(不符合题意,舍去);
②当时,为等腰三角形,
则,即,
解得或(不符合题意,舍去);
③当时,为等腰三角形,
则,即,
解得,
综上,或或.
(3)解:,
,
①当时,
则,即,
解得或(不符合题意,舍去),
将代入得:,
则此时点的坐标为;
②当时,
则,即,
解得或,
将代入得:,
将代入得:,
则此时点的坐标为或;
综上,存在这样的点,此时点的坐标为或或.
【点睛】本题考查了二次函数的几何应用、一次函数的几何应用、相似三角形的性质、等腰三角形等知识点,较难的是题(3),正确分情况讨论是解题关键.
18.(1)400,15
(2)54°,图见解析
(3)
【分析】(1)根据的人数以及百分比即可求得总人数,根据统计表即可求得的值;
(2)根据的百分比乘以360°即可求解,根据D的百分比求得人数,然后补全统计图即可;
(3)根据列表法求概率即可求解.
【详解】(1)本次参与调查的学生共有(人),
;
(2)扇形统计图中扇形B的圆心角度数为,
人数为140,条形统计图如图;
(3)列表如图,用A表示男生,B表示女生,
A1 A2 A3 B
A1 A1A2 A1A3 A1B
A2 A2A1 A2A3 A2B
A3 A3A1 A3A2 A3B
B BA1 BA2 BA3
所以,恰好选中“1男1女”的概率为.
【点睛】本题考查的是条形统计图和扇形统计图的综合运用,列表法求概率,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
19.(1)
(2)
(3)①;②为定值,,理由见解析
【分析】(1)如图所示,过点O作于D,连接,理由等边三角形的性质和圆周角定理以及垂径定理求出,,再根据勾股定理和含30度角的直角三角形的性质得到,据此求解即可;
(2)如图所示,延长交于F,连接,根据三角形中位线定理得到,再证明,,则,理由勾股定理求出,设,则,在中,,即可求出,在中,;
(3)①如图所示,如图所示,连接, 同理可得,由D,E是线段的三等分点,得到,证明,得到,则;②由,得到,再由,,得到,即可证明,则.
【详解】(1)解:如图所示,过点O作于D,连接,
∵是等边三角形,
∴,
∴,
∵,
∴,,
∴,
∴,
∴,
∴,
∴;
(2)解:如图所示,延长交于F,连接,
∵D,E分别是的中点,
∴是的中位线,
∴,,
∵点O是等腰三角形的外接圆圆心,
∴,,
∴,
∴,
设,则,
在中,,
∴,
∴,
在中,;
(3)解:①如图所示,如图所示,连接,
同理可得,
∵D,E是线段的三等分点,
∴,
∵,
∴,
∴,
∵D是的中点,
∴,
∴,
∴;
②,理由如下:
由①得,
∴,
∵D是的中点,
∴,
∴,
∵D,E是线段的三等分点,
∴,,
∴,
∵,
∴,
∴.
【点睛】本题主要考查了垂径定理,勾股定理,圆周角定理,三角形外接圆,相似三角形的性质与判定,三角形中位线定理等等,灵活运用所学知识是解题的关键.
20.(1)抛物线的解析式为
(2)抛物线与轴的交点坐标为
(3)时,函数值随着的增大而减小
【分析】(1)设顶点式,然后把代入求出的值即可;
(2)计算自变量的值为所对应的函数值即可;
(3)根据二次函数的性质解决问题.
【详解】(1)设抛物线的解析式为,
把代入得,
解得,
抛物线的解析式为;
(2)当时,,
抛物线与轴的交点坐标为;
(3)抛物线的对称轴为直线,抛物线开口向下,
当时,函数值随着的增大而减小.
【点睛】本题考查了待定系数法求二次函数的解析式;解题的关键是在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解,数量掌握二次函数的性质.
21.(1);
(2)
【分析】(1)直接由概率公式求解即可;
(2)用列表法列举出9种可能结果,其中一局游戏中两人出现平局的结果有3种,再由概率公式求解.
【详解】(1)解:在一局游戏中,小明决定出“剪刀”, 他赢爸爸的概率是;
(2)解:列表如下:
石头 剪刀 布
石头 (石头,石头) (石头,剪刀) (石头,布)
剪刀 (剪刀,石头) (剪刀,剪刀) (剪刀,布)
布 (布,石头) (布,剪刀) (布,布)
总共有9种可能,其中一局游戏中出现平局的有3种(剪刀,剪刀)(石头,石头)(布,布),
所以一局游戏中两人出现平局的概率为P=.
【点睛】本题考查了列表法求概率,概率=所求情况数÷总情况数,数据概率公式是解题的关键.
22.(1)见解析
(2)见解析
(3)
【分析】(1)根据网格结构找出点A、B绕点C旋转后的对应点、的位置,然后顺次连接即可;
(2)根据A对应点的坐标为,得出先向右平移3个单位再向下平移6个单位到,找出平移后的对应点、、的位置,然后顺次连接即可;
(3)根据旋转的定义结合图形,连接两对对应点,交点即为旋转中心.
【详解】(1)解:即为所求作的三角形,如图所示:
(2)解:即为所求,如图所示:
(3)解:如图,旋转中心P为;
故答案为:.
【点睛】本题主要考查平移作图和旋转作图,解题的关键是作出平移或旋转后对应点的位置
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
