2023-2024学年河南省驻马店市泌阳县八年级(上)期末数学模拟试卷(含解析)
文档属性
| 名称 | 2023-2024学年河南省驻马店市泌阳县八年级(上)期末数学模拟试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 311.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-30 01:32:36 | ||
图片预览

文档简介
2023-2024学年河南省驻马店市泌阳县八年级(上)期末数学模拟试卷
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)下列统计图中,最宜反映人体体温变化的是( )
A.折线统计图 B.条形统计图
C.扇形统计图 D.频数分布直方图
2.(3分)下列说法中正确的是( )
A.81的平方根是9 B.的算术平方根是4
C.与相等 D.64的立方根是±4
3.(3分)在△ABC中,已知D为直线BC上一点,若∠ABC=α,∠BAD=β,且AB=AC=CD,则β与α之间不可能存在的关系式是( )
A.β=90°α B.β=180°α
C.β D.β=120°α
4.(3分)下列各式计算正确的是( )
A.a+3a2=3a3 B.(a﹣b)2=a2﹣ab+b2
C.2(a﹣b)=2a﹣2b D.(2ab)2÷ab=2ab
5.(3分)如图,Rt△ABC,∠ACB=90°,∠ABC的角平分线和∠ACN的角平分线相交于点D,过D点作DE⊥BC于E.若AC=5,BC=12,AB=13,则DE=( )
A.2 B.3 C.3.5 D.4
6.(3分)《九章算术》是我国古代一部著名的数学专著,其中记载了一个“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺,问折者高几何?其意思是:有一根与地面垂直且高一丈的竹子(1丈=10尺),现被大风折断成两截,尖端落在地面上,竹尖与竹根的距离为三尺.问折断处高地面的距离为( )
A.5.45尺 B.4.55尺 C.5.8尺 D.4.2尺
7.(3分)用反证法证明“是无理数”时,最恰当的证法是先假设( )
A.是分数 B.是整数 C.是有理数 D.是实数
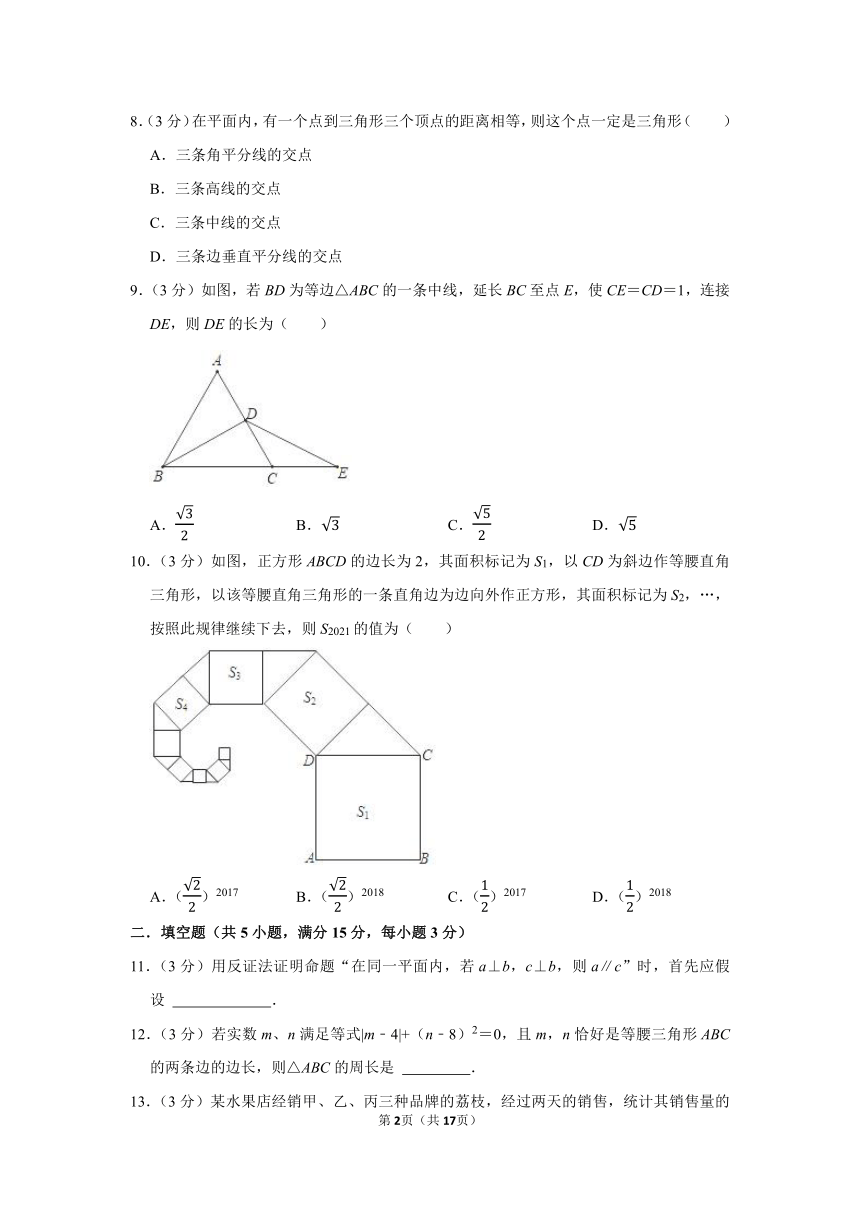
8.(3分)在平面内,有一个点到三角形三个顶点的距离相等,则这个点一定是三角形( )
A.三条角平分线的交点
B.三条高线的交点
C.三条中线的交点
D.三条边垂直平分线的交点
9.(3分)如图,若BD为等边△ABC的一条中线,延长BC至点E,使CE=CD=1,连接DE,则DE的长为( )
A. B. C. D.
10.(3分)如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…,按照此规律继续下去,则S2021的值为( )
A.()2017 B.()2018 C.()2017 D.()2018
二.填空题(共5小题,满分15分,每小题3分)
11.(3分)用反证法证明命题“在同一平面内,若a⊥b,c⊥b,则a∥c”时,首先应假设 .
12.(3分)若实数m、n满足等式|m﹣4|+(n﹣8)2=0,且m,n恰好是等腰三角形ABC的两条边的边长,则△ABC的周长是 .
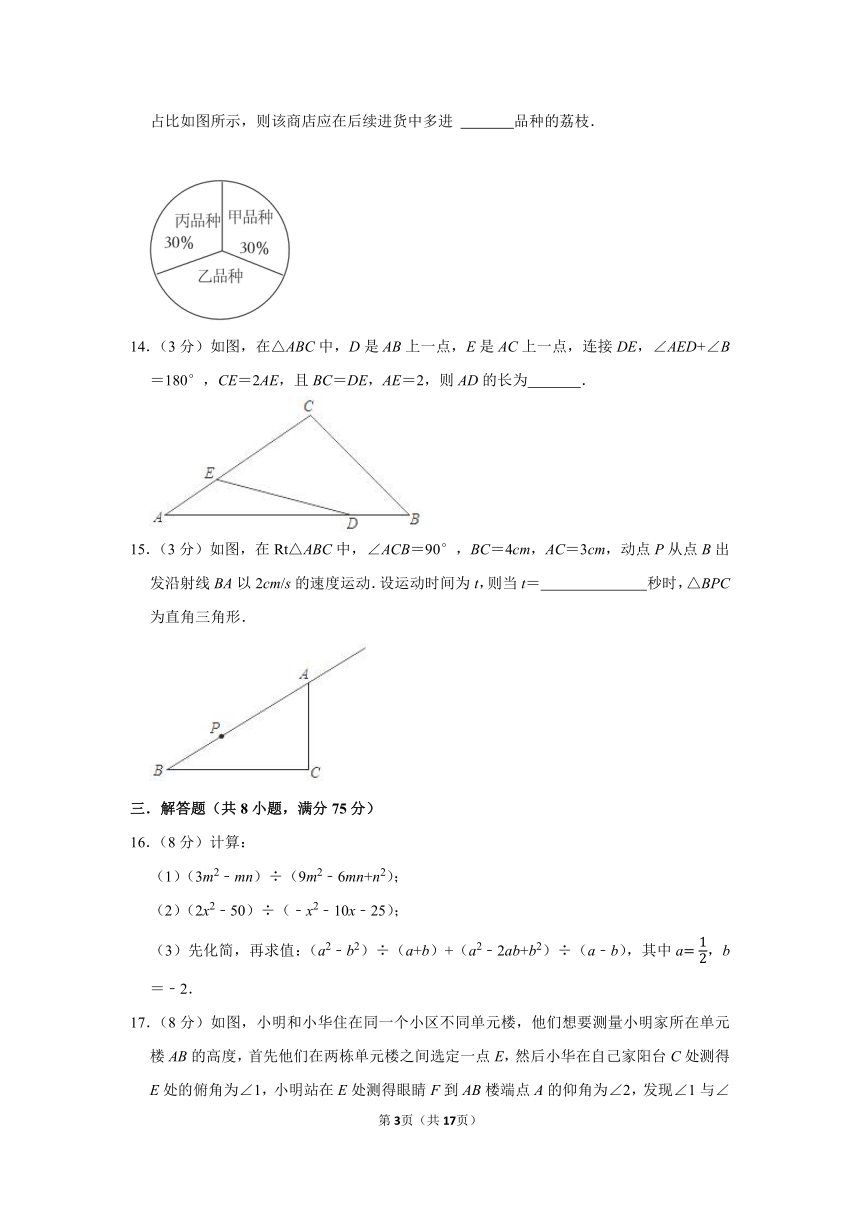
13.(3分)某水果店经销甲、乙、丙三种品牌的荔枝,经过两天的销售,统计其销售量的占比如图所示,则该商店应在后续进货中多进 品种的荔枝.
14.(3分)如图,在△ABC中,D是AB上一点,E是AC上一点,连接DE,∠AED+∠B=180°,CE=2AE,且BC=DE,AE=2,则AD的长为 .
15.(3分)如图,在Rt△ABC中,∠ACB=90°,BC=4cm,AC=3cm,动点P从点B出发沿射线BA以2cm/s的速度运动.设运动时间为t,则当t= 秒时,△BPC为直角三角形.
三.解答题(共8小题,满分75分)
16.(8分)计算:
(1)(3m2﹣mn)÷(9m2﹣6mn+n2);
(2)(2x2﹣50)÷(﹣x2﹣10x﹣25);
(3)先化简,再求值:(a2﹣b2)÷(a+b)+(a2﹣2ab+b2)÷(a﹣b),其中a,b=﹣2.
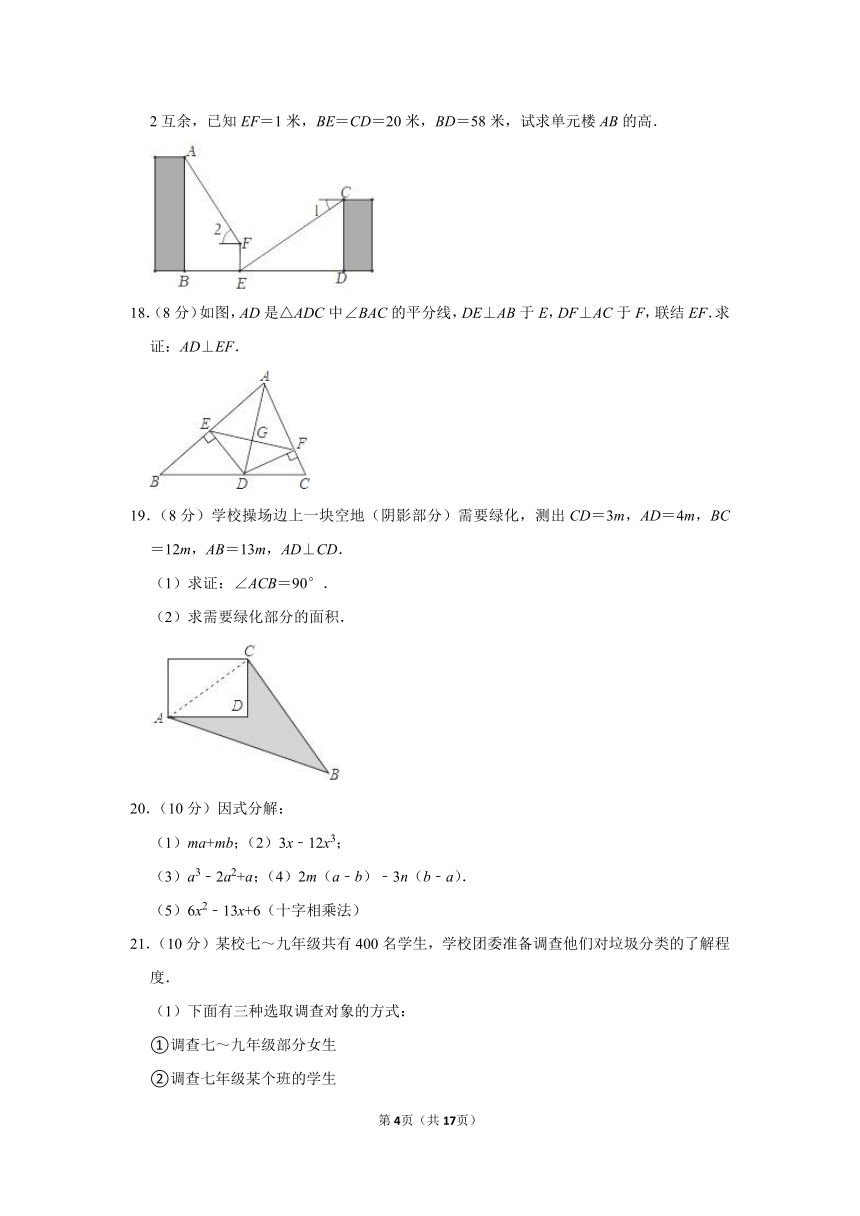
17.(8分)如图,小明和小华住在同一个小区不同单元楼,他们想要测量小明家所在单元楼AB的高度,首先他们在两栋单元楼之间选定一点E,然后小华在自己家阳台C处测得E处的俯角为∠1,小明站在E处测得眼睛F到AB楼端点A的仰角为∠2,发现∠1与∠2互余,已知EF=1米,BE=CD=20米,BD=58米,试求单元楼AB的高.
18.(8分)如图,AD是△ADC中∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,联结EF.求证:AD⊥EF.
19.(8分)学校操场边上一块空地(阴影部分)需要绿化,测出CD=3m,AD=4m,BC=12m,AB=13m,AD⊥CD.
(1)求证:∠ACB=90°.
(2)求需要绿化部分的面积.
20.(10分)因式分解:
(1)ma+mb;(2)3x﹣12x3;
(3)a3﹣2a2+a;(4)2m(a﹣b)﹣3n(b﹣a).
(5)6x2﹣13x+6(十字相乘法)
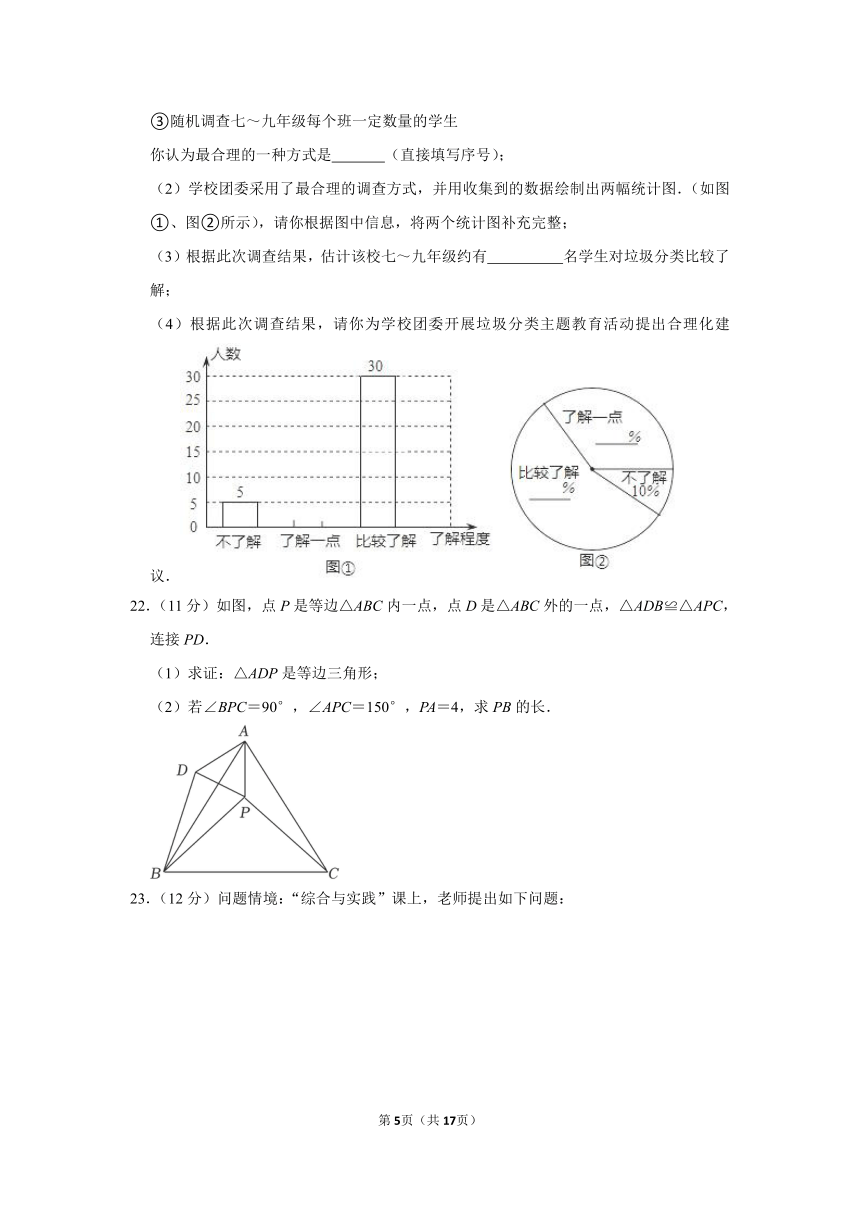
21.(10分)某校七~九年级共有400名学生,学校团委准备调查他们对垃圾分类的了解程度.
(1)下面有三种选取调查对象的方式:
①调查七~九年级部分女生
②调查七年级某个班的学生
③随机调查七~九年级每个班一定数量的学生
你认为最合理的一种方式是 (直接填写序号);
(2)学校团委采用了最合理的调查方式,并用收集到的数据绘制出两幅统计图.(如图①、图②所示),请你根据图中信息,将两个统计图补充完整;
(3)根据此次调查结果,估计该校七~九年级约有 名学生对垃圾分类比较了解;
(4)根据此次调查结果,请你为学校团委开展垃圾分类主题教育活动提出合理化建议.
22.(11分)如图,点P是等边△ABC内一点,点D是△ABC外的一点,△ADB≌△APC,连接PD.
(1)求证:△ADP是等边三角形;
(2)若∠BPC=90°,∠APC=150°,PA=4,求PB的长.
23.(12分)问题情境:“综合与实践”课上,老师提出如下问题:
将图1中的矩形纸片沿对角线剪开,得到两个全等的三角形纸片,表示为△ABC和△DFE,其中∠ACB=∠DEF=90°,∠A=∠D.将△ABC和△DFE按图2所示方式摆放,其中点B与点F重合(标记为点B).当∠ABE=∠A时,延长DE交AC于点G.
(1)试判断四边形BCGE的形状,并说明理由;
(2)深入探究:老师将图2中的△DBE绕点B逆时针方向旋转,使点E落在△ABC内部.
①“善思小组”提出问题:如图3,当∠ABE=∠BAC时,过点A作AM⊥BE交BE的延长线于点M,BM与AC交于点N.试猜想线段AM和BE的数量关系,并加以证明;
②“智慧小组”提出问题:如图4,当∠CBE=∠BAC时,过点A作AH⊥DE于点H,若BC=9,AC=12,求AH的长.
2023-2024学年河南省驻马店市泌阳县八年级(上)期末数学模拟试卷
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.【解答】解:最宜反映人体体温变化的是:折线统计图,
故选:A.
2.【解答】解:A:81的平方根是±9,∴不符合题意;
B:的算术平方根是2,∴不符合题意;
C:与相等,∴符合题意;
D:64的立方根是4,∴不符合题意;
故选:C.
3.【解答】解:当点D在线段BC上,
∵∠ABC=α,CA=AB,
∴∠C=∠ABC=α,
∵CD=CA,
∴∠ADC=∠CAD90°α,
∵∠ADC=∠B+∠BAD,
∴90°α=α+β,
即β=90°α;
当点D在线段BC的延长线上,
同理可得:β=180°α;
当点D在线段CB的延长线上,
同理可得:βα﹣90°.
故选:D.
4.【解答】解:A、原式不能合并,不符合题意;
B、原式=a2﹣2ab+b2,不符合题意;
C、原式=2a﹣2b,符合题意;
D、原式=4a2b2÷ab=4ab,不符合题意,
故选:C.
5.【解答】解:如图,连接AD,过点D作DK⊥AC于K,DJ⊥BA于J.
∵∠ABC的角平分线和∠ACN的角平分线相交于点D,
∴DJ=DE=DK,
∵∠ACB=90°,AC=5,BC=12,AB=13,S△ABC=S△DCB+S△ABD﹣S△ADC,
∴5×1212×DE13×DE5×DE,
解得DE=3,
故选:B.
6.【解答】解:设折断后的竹子高AC为x尺,则AB长为(10﹣x)尺,根据勾股定理得:
AC2+BC2=AB2,
即:x2+32=(10﹣x)2,
解得:x=4.55,
故选:B.
7.【解答】解:反证法证明“是无理数”时,先假设是有理数,
故选:C.
8.【解答】解:∵点到三角形三个顶点的距离相等,
∴这个点一定是三角形三条边的垂直平分线的交点,
故选:D.
9.【解答】解:∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,AB=BC,
∵BD为中线,
∴∠DBC∠ABC=30°,
∵CD=CE,
∴∠E=∠CDE,
∵∠E+∠CDE=∠ACB,
∴∠E=30°=∠DBC,
∴BD=DE,
∵BD是AC中线,CD=1,
∴AD=DC=1,
∵△ABC是等边三角形,
∴BC=AC=1+1=2,BD⊥AC,
在Rt△BDC中,由勾股定理得:BD,
即DE=BD,
故选:B.
10.【解答】解:如图所示,
∵△CDE是等腰直角三角形,
∴DE=CE,∠CED=90°,
∴CD2=DE2+CE2=2DE2,
∴DECD,
即等腰直角三角形的直角边为斜边的倍,
∴S1=22=4=4×()0,
S2=(2)2=2=4×()1,
S3=()2=1=4×()2,
S4=(1)24×()3,
…,
∴Sn=4×()n﹣1,
∴S2021=4×()2020=()2018.
故选:D.
二.填空题(共5小题,满分15分,每小题3分)
11.【解答】解:反证法证明命题“在同一平面内,若a⊥b,c⊥b,则a∥c”时,
首先应假设a与c不平行,
故答案为:a与c不平行.
12.【解答】解:∵|m﹣4|+(n﹣8)2=0,
∴m﹣4=0,n﹣8=0,
解得m=4,n=8,
当m=4作腰时,三边为4,4,8,不符合三边关系定理;
当n=8作腰时,三边为4,8,8,符合三边关系定理,周长为:4+8+8=20.
故答案为:20.
13.【解答】解:由扇形统计图可知:乙品种的百分比为:1﹣30%﹣30%=40%,
40%>30%,
说明乙品种荔枝销售较好,因此后续进货中多进乙品种的荔枝.
14.【解答】解:如图,作∠CHB=∠B,
∴CH=BC,BC=DE,
∴DE=CH,
∵AE=2,CE=2AE,
∴CE=4,AC=6,
∵∠AED+∠B=180°,∠CHB+∠AHC=180°,
∴∠AED=∠AHC,且∠A=∠A,DE=CH,
∴△ADE≌△ACH(AAS)
∴AD=AC=6,
故答案为:6.
15.【解答】解:在Rt△ABC中,∠ACB=90°,BC=4cm,AC=3cm,
∴AB5(cm).
如图,作AB边上的高CD.
∵S△ABCAB CDAC BC,
∴CD(cm).
①当∠BCP为直角时,点P与点A重合,BP=BA=5cm,
∴t=5÷2=2.5(秒).
②当∠BPC为直角时,P与D重合,BP=2t cm,CPcm,BC=4cm,
在Rt△BCP中,∵BP2+CP2=BC2,
∴(2t)2+()2=42,
解得t=1.6.
综上,当t=2.5或1.6秒时,△BPC为直角三角形.
故答案为:2.5或1.6.
三.解答题(共8小题,满分75分)
16.【解答】解:(1)(3m2﹣mn)÷(9m2﹣6mn+n2)
;
(2)(2x2﹣50)÷(﹣x2﹣10x﹣25)
;
(3)(a2﹣b2)÷(a+b)+(a2﹣2ab+b2)÷(a﹣b)
=(a+b)(a﹣b)÷(a+b)+(a﹣b)2÷(a﹣b)
=a﹣b+a﹣b
=2a﹣2b,
当a,b=﹣2时,原式=22×(﹣2)=5.
17.【解答】解:过F作FG⊥AB于G,
则四边形BEFG是矩形,
∴FG=BE=20米,BG=EF=1米,
∵∠1+∠2=90°,∠1+∠3=90°,
∴∠2=∠3,
在△AFG与△ECD中,
,
∴△AFG≌△ECD(ASA),
∴AG=DE=BD﹣BE=38(米),
∴AB=AG+BG=38+1=39(米),
答:单元楼AB的高为39米.
18.【解答】证明:如图所示:
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°,
又∵AD是△ADC中∠BAC的平分线,
∴DE=DF,
在Rt△AED和Rt△AFD中
,
∴Rt△AED≌Rt△AFD(HL),
∴Rt△AED与Rt△AFD关于直线AD成轴对称,
∴EF⊥AD.
19.【解答】(1)证明:∵AD⊥CD,
∴△ACD为直角三角形,
由勾股定理得:AC2=CD2+AD2,
∵CD=3m,AD=4m,
∴AC=5m,
在△ABC中,AB2=132=169,BC2=122=144,AC2=52=25,
∴AB2=BC2+AC2,
∴△ACB为直角三角形,
∴∠ACB=90°.
(2)解:S阴=S△ABC﹣S△ACD
AC BCCD AD
=30﹣6
=24(m2);
故需要绿化的面积为24m2.
20.【解答】解:(1)ma+mb=m(a+b)
(2)3x﹣12x3
=3x(1﹣4x2)
=3x(1+2x)(1﹣2x)
(3)a3﹣2a2+a
=a(a2﹣2a+1)
=a(a﹣1)2
(4)2m(a﹣b)﹣3n(b﹣a)
=2m(a﹣b)+3n(a﹣b)
=(2m+3n)(a﹣b)
(5)6x2﹣13x+6
=(2x﹣3)(3x﹣2)
21.【解答】解:(1)根据选择“样本”的广泛性、代表性和可操作性可得,最合理的调查方式是③,
故答案为:③;
(2)5÷10%=50(人),50﹣5﹣30=15(人),15÷50=30%,30÷50=60%,补全统计图如图所示;
(3)400×60%=240(人),
故答案为:240;
(4)“了解一点”所占的比为60%,应该加强宣传和培训,增强对垃圾分类的了解程度.
22.【解答】(1)证明:∵△ADB≌△APC,
∴AD=AP,∠CAP=∠BAD,
∴∠DAP=∠DAB+∠BAP=∠BAP+∠CAP=60°,
∴△ADP是等边三角形;
(2)解:由(1)知,△ADP是等边三角形,
∴∠APD=∠ADP=60°,PD=PA=4,
∵∠BPC=90°,∠APC=150°,
∴∠DPB=360°﹣∠APD﹣∠APC﹣∠BPC=60°,
∵△ADB≌△APC,
∴∠ADB=∠APC=150°,
∴∠BDP=90°,
∴PB=2PD=8.
23.【解答】解:(1)四边形BCGE为正方形.理由如下:
∵∠BED=90°,
∴∠BEG=180°﹣∠BED=90°,
∵∠ABE=∠A,
∴AC∥BE,
∴∠CGE=∠BED=90°,
∵∠C=90°,
∴四边形BCGE为矩形,
∵△ACB≌△DEB,
∴BC=BE,
∴矩形BCGE为正方形;
(2)①AM=BE,理由如下:
∵∠ABE=∠BAC,
∴AN=BN,
∵∠C=90°,
∴BC⊥AN,
∵AM⊥BE,即AM⊥BN,
∴S△ABNAN BCBN AM,
∵AN=BN,
∴BC=AM,
由(1)得BE=BC,
∴AM=BE;
②如图4,设AB,DE的交点为M,过M作MG⊥BD于G,
∵△ACB≌△DEB,
∴BE=BC=9,DE=AC=12,∠BAC=∠D,∠ABC=∠DBE,
∴∠CBE=∠DBM;
∵∠CBE=∠BAC,
∴∠DBM=∠BAC,
∴∠DBM=∠D,
∴MD=MB,
∵MG⊥BD,
∴点G是BD的中点;
由勾股定理得AB15,
∴DGBD;
∵cosD,
∴DM,即BM=DM;
∴AM=AB﹣BM=15;
∵AH⊥DE,BE⊥DE,
∴∠AHM=∠BEM=90°,
∵∠AMH=∠BME,
∴△AMH∽△BME,
∴,
∴AHBE9,即AH的长为.
第1页(共1页)
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)下列统计图中,最宜反映人体体温变化的是( )
A.折线统计图 B.条形统计图
C.扇形统计图 D.频数分布直方图
2.(3分)下列说法中正确的是( )
A.81的平方根是9 B.的算术平方根是4
C.与相等 D.64的立方根是±4
3.(3分)在△ABC中,已知D为直线BC上一点,若∠ABC=α,∠BAD=β,且AB=AC=CD,则β与α之间不可能存在的关系式是( )
A.β=90°α B.β=180°α
C.β D.β=120°α
4.(3分)下列各式计算正确的是( )
A.a+3a2=3a3 B.(a﹣b)2=a2﹣ab+b2
C.2(a﹣b)=2a﹣2b D.(2ab)2÷ab=2ab
5.(3分)如图,Rt△ABC,∠ACB=90°,∠ABC的角平分线和∠ACN的角平分线相交于点D,过D点作DE⊥BC于E.若AC=5,BC=12,AB=13,则DE=( )
A.2 B.3 C.3.5 D.4
6.(3分)《九章算术》是我国古代一部著名的数学专著,其中记载了一个“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺,问折者高几何?其意思是:有一根与地面垂直且高一丈的竹子(1丈=10尺),现被大风折断成两截,尖端落在地面上,竹尖与竹根的距离为三尺.问折断处高地面的距离为( )
A.5.45尺 B.4.55尺 C.5.8尺 D.4.2尺
7.(3分)用反证法证明“是无理数”时,最恰当的证法是先假设( )
A.是分数 B.是整数 C.是有理数 D.是实数
8.(3分)在平面内,有一个点到三角形三个顶点的距离相等,则这个点一定是三角形( )
A.三条角平分线的交点
B.三条高线的交点
C.三条中线的交点
D.三条边垂直平分线的交点
9.(3分)如图,若BD为等边△ABC的一条中线,延长BC至点E,使CE=CD=1,连接DE,则DE的长为( )
A. B. C. D.
10.(3分)如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…,按照此规律继续下去,则S2021的值为( )
A.()2017 B.()2018 C.()2017 D.()2018
二.填空题(共5小题,满分15分,每小题3分)
11.(3分)用反证法证明命题“在同一平面内,若a⊥b,c⊥b,则a∥c”时,首先应假设 .
12.(3分)若实数m、n满足等式|m﹣4|+(n﹣8)2=0,且m,n恰好是等腰三角形ABC的两条边的边长,则△ABC的周长是 .
13.(3分)某水果店经销甲、乙、丙三种品牌的荔枝,经过两天的销售,统计其销售量的占比如图所示,则该商店应在后续进货中多进 品种的荔枝.
14.(3分)如图,在△ABC中,D是AB上一点,E是AC上一点,连接DE,∠AED+∠B=180°,CE=2AE,且BC=DE,AE=2,则AD的长为 .
15.(3分)如图,在Rt△ABC中,∠ACB=90°,BC=4cm,AC=3cm,动点P从点B出发沿射线BA以2cm/s的速度运动.设运动时间为t,则当t= 秒时,△BPC为直角三角形.
三.解答题(共8小题,满分75分)
16.(8分)计算:
(1)(3m2﹣mn)÷(9m2﹣6mn+n2);
(2)(2x2﹣50)÷(﹣x2﹣10x﹣25);
(3)先化简,再求值:(a2﹣b2)÷(a+b)+(a2﹣2ab+b2)÷(a﹣b),其中a,b=﹣2.
17.(8分)如图,小明和小华住在同一个小区不同单元楼,他们想要测量小明家所在单元楼AB的高度,首先他们在两栋单元楼之间选定一点E,然后小华在自己家阳台C处测得E处的俯角为∠1,小明站在E处测得眼睛F到AB楼端点A的仰角为∠2,发现∠1与∠2互余,已知EF=1米,BE=CD=20米,BD=58米,试求单元楼AB的高.
18.(8分)如图,AD是△ADC中∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,联结EF.求证:AD⊥EF.
19.(8分)学校操场边上一块空地(阴影部分)需要绿化,测出CD=3m,AD=4m,BC=12m,AB=13m,AD⊥CD.
(1)求证:∠ACB=90°.
(2)求需要绿化部分的面积.
20.(10分)因式分解:
(1)ma+mb;(2)3x﹣12x3;
(3)a3﹣2a2+a;(4)2m(a﹣b)﹣3n(b﹣a).
(5)6x2﹣13x+6(十字相乘法)
21.(10分)某校七~九年级共有400名学生,学校团委准备调查他们对垃圾分类的了解程度.
(1)下面有三种选取调查对象的方式:
①调查七~九年级部分女生
②调查七年级某个班的学生
③随机调查七~九年级每个班一定数量的学生
你认为最合理的一种方式是 (直接填写序号);
(2)学校团委采用了最合理的调查方式,并用收集到的数据绘制出两幅统计图.(如图①、图②所示),请你根据图中信息,将两个统计图补充完整;
(3)根据此次调查结果,估计该校七~九年级约有 名学生对垃圾分类比较了解;
(4)根据此次调查结果,请你为学校团委开展垃圾分类主题教育活动提出合理化建议.
22.(11分)如图,点P是等边△ABC内一点,点D是△ABC外的一点,△ADB≌△APC,连接PD.
(1)求证:△ADP是等边三角形;
(2)若∠BPC=90°,∠APC=150°,PA=4,求PB的长.
23.(12分)问题情境:“综合与实践”课上,老师提出如下问题:
将图1中的矩形纸片沿对角线剪开,得到两个全等的三角形纸片,表示为△ABC和△DFE,其中∠ACB=∠DEF=90°,∠A=∠D.将△ABC和△DFE按图2所示方式摆放,其中点B与点F重合(标记为点B).当∠ABE=∠A时,延长DE交AC于点G.
(1)试判断四边形BCGE的形状,并说明理由;
(2)深入探究:老师将图2中的△DBE绕点B逆时针方向旋转,使点E落在△ABC内部.
①“善思小组”提出问题:如图3,当∠ABE=∠BAC时,过点A作AM⊥BE交BE的延长线于点M,BM与AC交于点N.试猜想线段AM和BE的数量关系,并加以证明;
②“智慧小组”提出问题:如图4,当∠CBE=∠BAC时,过点A作AH⊥DE于点H,若BC=9,AC=12,求AH的长.
2023-2024学年河南省驻马店市泌阳县八年级(上)期末数学模拟试卷
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.【解答】解:最宜反映人体体温变化的是:折线统计图,
故选:A.
2.【解答】解:A:81的平方根是±9,∴不符合题意;
B:的算术平方根是2,∴不符合题意;
C:与相等,∴符合题意;
D:64的立方根是4,∴不符合题意;
故选:C.
3.【解答】解:当点D在线段BC上,
∵∠ABC=α,CA=AB,
∴∠C=∠ABC=α,
∵CD=CA,
∴∠ADC=∠CAD90°α,
∵∠ADC=∠B+∠BAD,
∴90°α=α+β,
即β=90°α;
当点D在线段BC的延长线上,
同理可得:β=180°α;
当点D在线段CB的延长线上,
同理可得:βα﹣90°.
故选:D.
4.【解答】解:A、原式不能合并,不符合题意;
B、原式=a2﹣2ab+b2,不符合题意;
C、原式=2a﹣2b,符合题意;
D、原式=4a2b2÷ab=4ab,不符合题意,
故选:C.
5.【解答】解:如图,连接AD,过点D作DK⊥AC于K,DJ⊥BA于J.
∵∠ABC的角平分线和∠ACN的角平分线相交于点D,
∴DJ=DE=DK,
∵∠ACB=90°,AC=5,BC=12,AB=13,S△ABC=S△DCB+S△ABD﹣S△ADC,
∴5×1212×DE13×DE5×DE,
解得DE=3,
故选:B.
6.【解答】解:设折断后的竹子高AC为x尺,则AB长为(10﹣x)尺,根据勾股定理得:
AC2+BC2=AB2,
即:x2+32=(10﹣x)2,
解得:x=4.55,
故选:B.
7.【解答】解:反证法证明“是无理数”时,先假设是有理数,
故选:C.
8.【解答】解:∵点到三角形三个顶点的距离相等,
∴这个点一定是三角形三条边的垂直平分线的交点,
故选:D.
9.【解答】解:∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,AB=BC,
∵BD为中线,
∴∠DBC∠ABC=30°,
∵CD=CE,
∴∠E=∠CDE,
∵∠E+∠CDE=∠ACB,
∴∠E=30°=∠DBC,
∴BD=DE,
∵BD是AC中线,CD=1,
∴AD=DC=1,
∵△ABC是等边三角形,
∴BC=AC=1+1=2,BD⊥AC,
在Rt△BDC中,由勾股定理得:BD,
即DE=BD,
故选:B.
10.【解答】解:如图所示,
∵△CDE是等腰直角三角形,
∴DE=CE,∠CED=90°,
∴CD2=DE2+CE2=2DE2,
∴DECD,
即等腰直角三角形的直角边为斜边的倍,
∴S1=22=4=4×()0,
S2=(2)2=2=4×()1,
S3=()2=1=4×()2,
S4=(1)24×()3,
…,
∴Sn=4×()n﹣1,
∴S2021=4×()2020=()2018.
故选:D.
二.填空题(共5小题,满分15分,每小题3分)
11.【解答】解:反证法证明命题“在同一平面内,若a⊥b,c⊥b,则a∥c”时,
首先应假设a与c不平行,
故答案为:a与c不平行.
12.【解答】解:∵|m﹣4|+(n﹣8)2=0,
∴m﹣4=0,n﹣8=0,
解得m=4,n=8,
当m=4作腰时,三边为4,4,8,不符合三边关系定理;
当n=8作腰时,三边为4,8,8,符合三边关系定理,周长为:4+8+8=20.
故答案为:20.
13.【解答】解:由扇形统计图可知:乙品种的百分比为:1﹣30%﹣30%=40%,
40%>30%,
说明乙品种荔枝销售较好,因此后续进货中多进乙品种的荔枝.
14.【解答】解:如图,作∠CHB=∠B,
∴CH=BC,BC=DE,
∴DE=CH,
∵AE=2,CE=2AE,
∴CE=4,AC=6,
∵∠AED+∠B=180°,∠CHB+∠AHC=180°,
∴∠AED=∠AHC,且∠A=∠A,DE=CH,
∴△ADE≌△ACH(AAS)
∴AD=AC=6,
故答案为:6.
15.【解答】解:在Rt△ABC中,∠ACB=90°,BC=4cm,AC=3cm,
∴AB5(cm).
如图,作AB边上的高CD.
∵S△ABCAB CDAC BC,
∴CD(cm).
①当∠BCP为直角时,点P与点A重合,BP=BA=5cm,
∴t=5÷2=2.5(秒).
②当∠BPC为直角时,P与D重合,BP=2t cm,CPcm,BC=4cm,
在Rt△BCP中,∵BP2+CP2=BC2,
∴(2t)2+()2=42,
解得t=1.6.
综上,当t=2.5或1.6秒时,△BPC为直角三角形.
故答案为:2.5或1.6.
三.解答题(共8小题,满分75分)
16.【解答】解:(1)(3m2﹣mn)÷(9m2﹣6mn+n2)
;
(2)(2x2﹣50)÷(﹣x2﹣10x﹣25)
;
(3)(a2﹣b2)÷(a+b)+(a2﹣2ab+b2)÷(a﹣b)
=(a+b)(a﹣b)÷(a+b)+(a﹣b)2÷(a﹣b)
=a﹣b+a﹣b
=2a﹣2b,
当a,b=﹣2时,原式=22×(﹣2)=5.
17.【解答】解:过F作FG⊥AB于G,
则四边形BEFG是矩形,
∴FG=BE=20米,BG=EF=1米,
∵∠1+∠2=90°,∠1+∠3=90°,
∴∠2=∠3,
在△AFG与△ECD中,
,
∴△AFG≌△ECD(ASA),
∴AG=DE=BD﹣BE=38(米),
∴AB=AG+BG=38+1=39(米),
答:单元楼AB的高为39米.
18.【解答】证明:如图所示:
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°,
又∵AD是△ADC中∠BAC的平分线,
∴DE=DF,
在Rt△AED和Rt△AFD中
,
∴Rt△AED≌Rt△AFD(HL),
∴Rt△AED与Rt△AFD关于直线AD成轴对称,
∴EF⊥AD.
19.【解答】(1)证明:∵AD⊥CD,
∴△ACD为直角三角形,
由勾股定理得:AC2=CD2+AD2,
∵CD=3m,AD=4m,
∴AC=5m,
在△ABC中,AB2=132=169,BC2=122=144,AC2=52=25,
∴AB2=BC2+AC2,
∴△ACB为直角三角形,
∴∠ACB=90°.
(2)解:S阴=S△ABC﹣S△ACD
AC BCCD AD
=30﹣6
=24(m2);
故需要绿化的面积为24m2.
20.【解答】解:(1)ma+mb=m(a+b)
(2)3x﹣12x3
=3x(1﹣4x2)
=3x(1+2x)(1﹣2x)
(3)a3﹣2a2+a
=a(a2﹣2a+1)
=a(a﹣1)2
(4)2m(a﹣b)﹣3n(b﹣a)
=2m(a﹣b)+3n(a﹣b)
=(2m+3n)(a﹣b)
(5)6x2﹣13x+6
=(2x﹣3)(3x﹣2)
21.【解答】解:(1)根据选择“样本”的广泛性、代表性和可操作性可得,最合理的调查方式是③,
故答案为:③;
(2)5÷10%=50(人),50﹣5﹣30=15(人),15÷50=30%,30÷50=60%,补全统计图如图所示;
(3)400×60%=240(人),
故答案为:240;
(4)“了解一点”所占的比为60%,应该加强宣传和培训,增强对垃圾分类的了解程度.
22.【解答】(1)证明:∵△ADB≌△APC,
∴AD=AP,∠CAP=∠BAD,
∴∠DAP=∠DAB+∠BAP=∠BAP+∠CAP=60°,
∴△ADP是等边三角形;
(2)解:由(1)知,△ADP是等边三角形,
∴∠APD=∠ADP=60°,PD=PA=4,
∵∠BPC=90°,∠APC=150°,
∴∠DPB=360°﹣∠APD﹣∠APC﹣∠BPC=60°,
∵△ADB≌△APC,
∴∠ADB=∠APC=150°,
∴∠BDP=90°,
∴PB=2PD=8.
23.【解答】解:(1)四边形BCGE为正方形.理由如下:
∵∠BED=90°,
∴∠BEG=180°﹣∠BED=90°,
∵∠ABE=∠A,
∴AC∥BE,
∴∠CGE=∠BED=90°,
∵∠C=90°,
∴四边形BCGE为矩形,
∵△ACB≌△DEB,
∴BC=BE,
∴矩形BCGE为正方形;
(2)①AM=BE,理由如下:
∵∠ABE=∠BAC,
∴AN=BN,
∵∠C=90°,
∴BC⊥AN,
∵AM⊥BE,即AM⊥BN,
∴S△ABNAN BCBN AM,
∵AN=BN,
∴BC=AM,
由(1)得BE=BC,
∴AM=BE;
②如图4,设AB,DE的交点为M,过M作MG⊥BD于G,
∵△ACB≌△DEB,
∴BE=BC=9,DE=AC=12,∠BAC=∠D,∠ABC=∠DBE,
∴∠CBE=∠DBM;
∵∠CBE=∠BAC,
∴∠DBM=∠BAC,
∴∠DBM=∠D,
∴MD=MB,
∵MG⊥BD,
∴点G是BD的中点;
由勾股定理得AB15,
∴DGBD;
∵cosD,
∴DM,即BM=DM;
∴AM=AB﹣BM=15;
∵AH⊥DE,BE⊥DE,
∴∠AHM=∠BEM=90°,
∵∠AMH=∠BME,
∴△AMH∽△BME,
∴,
∴AHBE9,即AH的长为.
第1页(共1页)
