2023-2024学年西藏昌都第二高级中学八年级(上)期末数学模拟试卷(含解析)
文档属性
| 名称 | 2023-2024学年西藏昌都第二高级中学八年级(上)期末数学模拟试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 168.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-30 01:34:22 | ||
图片预览




文档简介
2023-2024学年西藏昌都第二高级中学八年级(上)期末数学模拟试卷
一.选择题(共12小题,满分36分,每小题3分)
1.(3分)下面四个手机APP图标中为轴对称图形的是( )
A. B. C. D.
2.(3分)要使分式有意义,则x的取值应该满足( )
A.x≠﹣5 B.x≠5 C.x=3 D.x≠0
3.(3分)下列计算正确的是( )
A.a2 a4=a6 B.(x﹣1)2=x2﹣1
C.3a2b﹣3ab2=0 D.(a2)5=a7
4.(3分)下列各数中,属于无理数的是( )
A. B.1.4141414 C. D.
5.(3分)不等式组的解集在数轴上表示正确的是( )
A.
B.
C.
D.
6.(3分)已知:等腰三角形两边长分别为9cm,5cm,则周长是( )
A.19cm B.23cm
C.19cm或23cm D.不能确定
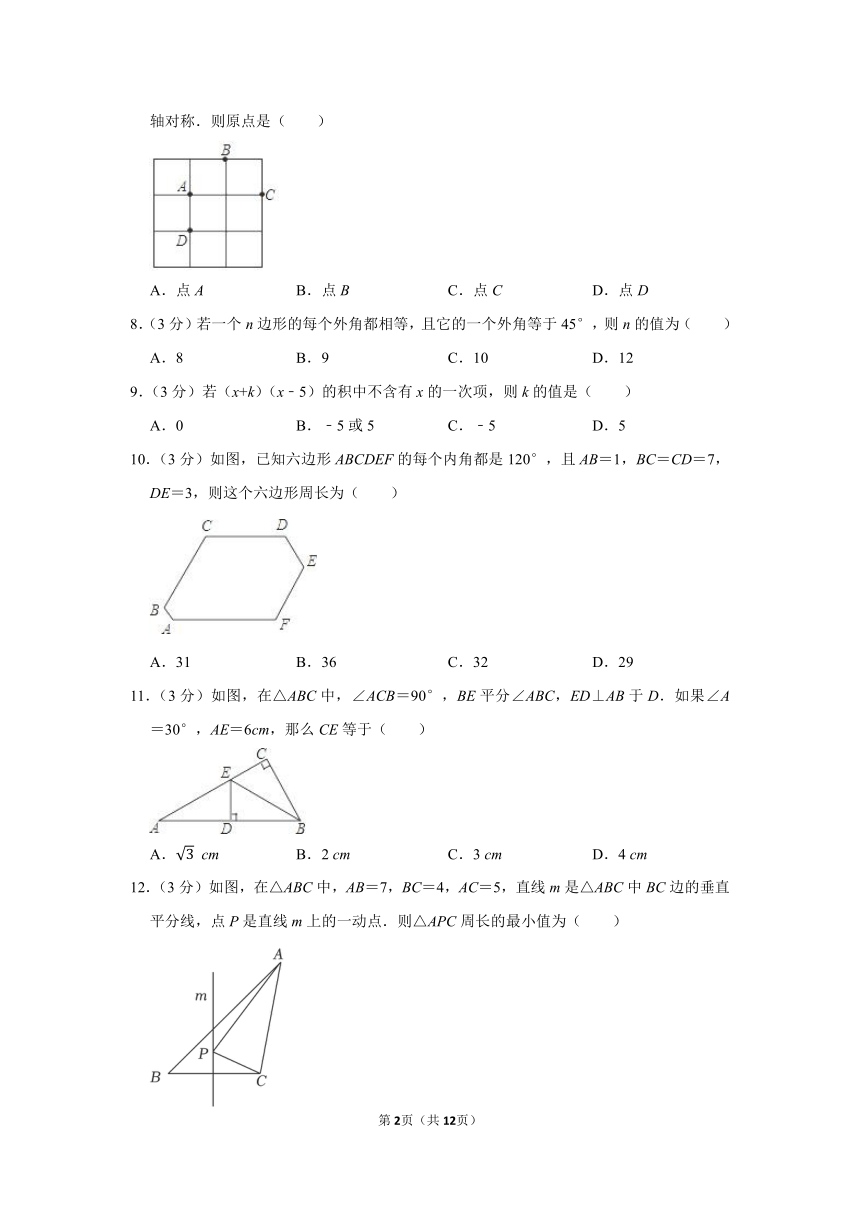
7.(3分)如图,在3×3的正方形网格中有4个格点A,B,C,D,以其中一点为原点,网格线所在直线为坐标轴,建立直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称.则原点是( )
A.点A B.点B C.点C D.点D
8.(3分)若一个n边形的每个外角都相等,且它的一个外角等于45°,则n的值为( )
A.8 B.9 C.10 D.12
9.(3分)若(x+k)(x﹣5)的积中不含有x的一次项,则k的值是( )
A.0 B.﹣5或5 C.﹣5 D.5
10.(3分)如图,已知六边形ABCDEF的每个内角都是120°,且AB=1,BC=CD=7,DE=3,则这个六边形周长为( )
A.31 B.36 C.32 D.29
11.(3分)如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于D.如果∠A=30°,AE=6cm,那么CE等于( )
A. cm B.2 cm C.3 cm D.4 cm
12.(3分)如图,在△ABC中,AB=7,BC=4,AC=5,直线m是△ABC中BC边的垂直平分线,点P是直线m上的一动点.则△APC周长的最小值为( )
A.9 B.11 C.12 D.13
二.填空题(共6小题,满分18分,每小题3分)
13.(3分)已知1+x+x2=0,那么1+x+x2+x3+…+x2008+x2009+x2010的值是 .
14.(3分)从10边形的一个顶点出发可以引 条对角线.
15.(3分)重庆市作为“网红城市”,在2019年国庆节期间接待游客数量高达38590000人次,请将数字38590000用科学记数法表示为 .
16.(3分)若x,y为有理数,且|x+2|+(y﹣2)2=0,则()2021的值为 .
17.(3分)若x xa xb xc=x2015,则a+b+c= .
18.(3分)若按一定规律排列的数据如下:x,x2,x3,x4,x5,…,则第n个数可用代数式表示为 .(n为正整数)
三.(共8小题,满分61分)
19.(6分)化简求值:2a(a+b)﹣(a+b)2,其中a=3,b.
20.(7分)解分式方程:1.
21.(8分)如图,△ABC的三个顶点的坐标分别为A(﹣5,5)、B(﹣6,1)、C(﹣1,4),△ABC与△A1B1C1关于x轴对称,△A1B1C1与△A2B2C2关于y轴对称,点A1、B1、C1分别是点A、B、C的对应点,点A2、B2、C2分别是点A1、B1、C1的对应点.
(1)画出△A1B1C1与△A2B2C2;
(2)连接AC2、B1C2、AB1,求△AB1C2的面积.
22.(10分)现在购物时常用的支付方式有:A微信、B支付宝、C现金、D其他.某数学兴趣小组随机调查了某社区部分居民的常用支付方式,得到两幅不完整的统计图.
请你根据统计图提供的信息,解答下列问题:
(1)本次调查的居民总人数是 人,扇形统计图中“方式A”所对应的圆心角是 度,并补全条形统计图;
(2)若该社区有2600名居民,请估计使用A和B两种支付方式的居民共有多少名?
23.(8分)如图,在四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD∥BC.
(1)求证:四边形ABCD是平行四边形.
(2)若AC⊥BD,且AB=3,则平行四边形ABCD的周长为 .
24.(6分)如图,△ABC中,AD是高,CE是角平分线,AD交CE于点P,已知,∠APE=55°,∠AEP=100°,
求△ABC的各个内角的度数.
25.(8分)为了保护环境,某市公交公司决定购买一批共10台全新的混合动力公交车,现有A、B两种型号,其中每台的价格,年省油量如表:
A B
价格(万元/台) a b
节省的油量(万升/年 台) 2.4 2
经调查,购买一台A型车比购买一台B型车多20万元,购买2台A型车比购买3台B型车少60万元
(1)请求出a和b的值;
(2)若购买这批混合动力公交车每年能节省22.4万升汽油,求购买这批混合动力公交车需要多少万元?
26.(8分)某校准备购进21套桌椅来筹建一间多功能教学实验室,现有两类桌椅可供选择:甲类桌椅是三角形桌,每桌可坐3人,乙类桌椅是五边形桌,每桌可坐5人.学校分两次进行采购,第一次采购甲、乙两类桌椅均是原价;第二次采购时,甲因原材料上涨提价了20%,乙因促销活动降价20%.两次采购的数量和费用如下表:
购买甲类桌椅/套 购买乙类桌椅/套 购买总费用/元
第一次采购 6 5 1950
第二次采购 3 7 1716
(1)求第一次采购时,甲、乙类桌椅每套的购买价格.
(2)若该校每班有学生42人,问:该多功能教学实验室最多能同时容纳几个班级开展活动?
(3)某班42位同学需使用该实验室,管理员要求使用的桌椅每套必须坐满,请你计算桌椅的使用数量最少时,使用甲、乙类桌椅分别多少套.
2023-2024学年西藏昌都第二高级中学八年级(上)期末数学模拟试卷
参考答案与试题解析
一.选择题(共12小题,满分36分,每小题3分)
1.【解答】解:A、不是轴对称图形,不符合题意;
B、不是轴对称图形,是中心对称图形,不符合题意;
C、是轴对称图形,符合题意;
D、不是轴对称图形,不符合题意.
故选:C.
2.【解答】解:∵分式有意义,
∴x+5≠0,
解得x≠﹣5.
故选:A.
3.【解答】解:A、原式=a6,符合题意;
B、原式=x2﹣2x+1,不符合题意;
C、原式不能合并,不符合题意;
D、原式=a10,不符合题意.
故选:A.
4.【解答】解:A、是分数,属于有理数;
B、1.4141414是有限小数,属于有理数;
C、是无理数;
D、,是整数,属于有理数.
故选:C.
5.【解答】解:由3x﹣9<0,得:x<3,
由4x+6≤22,得:x≤4,
则不等式组的解集为x<3,
故选:A.
6.【解答】解:①若9cm是腰长,则三角形的三边分别为9cm、9cm、5cm,
能组成三角形,
周长=9+9+5=23cm,
②若9cm是底边长,则三角形的三边分别为9cm、5cm、5cm,
能组成三角形,
周长=9+5+5=19cm,
综上所述,三角形的周长为23cm或19cm.
故选:C.
7.【解答】解:如图:
以B为坐标原点建立坐标系,点A和点C关于y轴对称,
故选:B.
8.【解答】解:∵多边形的外角和为360°,一个外角45°,
∴多边形得到边数360÷45=8,所以是八边形.
故选:A.
9.【解答】解:(x+k)(x﹣5)=x2﹣5x+kx﹣5k=x2+(k﹣5)x﹣5k,
由积中不含x的一次项,得到k﹣5=0,
解得:k=5.
故选:D.
10.【解答】解:如图,延长并反向延长AB,CD,EF,
∵六边形ABCDEF的每个内角都是120°,
∴∠G=∠H=∠N=60°,
∴△GHN,△GBC,△AFH、△DEN都是等边三角形,
∴GN=CG+CD+DN=BC+CD+DE=7+7+3=17,
∴六边形ABCDEF的周长=GH+HN+NG﹣EN﹣AH﹣BG=3×17﹣3﹣9﹣7=32.
故选:C.
11.【解答】解:∵ED⊥AB,∠A=30°,
∴DEAE=3cm,
∵BE平分∠ABC,ED⊥AB,∠ACB=90°,
∴CE=DE=3cm,
故选:C.
12.【解答】解:∵直线m垂直平分BC,
∴B、C关于直线m对称,
设直线m交AB于D,
∴当P和D重合时,AP+CP的值最小,最小值等于AB的长,
∴△APC周长的最小值是7+5=12.
故选:C.
二.填空题(共6小题,满分18分,每小题3分)
13.【解答】解:1+x+x2+x3+…+x2010=1+(x+x2+x3)+(x4+x5+x6)+ +(x2008+x2009+x2010)
=1+x(1+x+x2)+x4(1+x+x2)+…+x2005(1+x+x2)+x2008(1+x+x2)
=1+x×0+…+x2008×0
=1+0+…+0
=1.
故答案为:1.
14.【解答】解:从10边形的一个顶点出发可引10﹣3=7条对角线,
故答案为:7.
15.【解答】解:3859 0000=3.859×107.
故答案为:3.859×107.
16.【解答】解:∵|x+2|+(y﹣2)2=0,|x+2|≥0,(y﹣2)2≥0,
∴x+2=0,y﹣2=0,
解得x=﹣2,y=2,
∴()2021=(﹣1)2021=﹣1.
故答案为:﹣1.
17.【解答】解:由x xa xb xc=1+a+b+c=x2015,得
a+b+c=2015﹣1=2014,
故答案为:2014.
18.【解答】解:∵一列数为:x,x2,x3,x4,x5,…,
∴第n个数可以表示为:(﹣1)n+1xn,
故答案为:(﹣1)n+1xn.
三.(共8小题,满分61分)
19.【解答】解:原式=2a2+2ab﹣(a2+2ab+b2)
=2a2+2ab﹣a2﹣2ab﹣b2
=a2﹣b2,
当a=3,b时,
原式=32﹣()2
=9
.
20.【解答】解:1,
方程两边都乘(x+2)(x﹣2),得3(x﹣2)+(x+2)(x﹣2)=(x+2)2,
解得:x=﹣14,
检验:当x=﹣14时,(x+2)(x﹣2)≠0,
所以x=﹣14是原方程的解,
即原方程的解是x=﹣14.
21.【解答】解:(1)如图所示,△A1B1C1和△A2B2C2即为所求,
(2)∵,
∴△AB1C2的面积是22.5.
22.【解答】解:(1)调查总人数:56÷28%=200(人),
使用“方式D”的人数:200×20%=40(人),
使用“方式A”的人数:200﹣40﹣56﹣44=60(人),
使用“方式A”所对应的圆心角为:360°108°,
故答案为:200,108,补全条形统计图如下:
(2)26001508(名),
答:该社区有2600名居民中使用A和B两种支付方式的大约有1508名.
23.【解答】(1)证明:∵AD∥BC,
∴∠ADO=∠CBO,
∵O是AC的中点,
∴OA=OC.
在△AOD和△COB中,,
∴△AOD≌△COB(AAS),
∴OD=OB.
∵OA=OC,
∴四边形ABCD是平行四边形;
(2)解:∵四边形ABCD是平行四边形,
又∵AC⊥BD,
∴四边形ABCD是菱形,
∴BC=CD=AD=AB=3,
∴四边形ABCD的周长=4AB=12;
故答案为:12.
24.【解答】解:在△AEP中,∠BAD=180°﹣∠APE﹣∠AEP=180°﹣55°﹣100°=25°,
∵AD是高,
∴∠ADB=∠ADC=90°,
∴∠B=180°﹣∠BAD﹣∠ADB=65°,
∴∠BCE=∠AEP﹣∠B=35°.
∵CE是角平分线,
∴∠ACB=2∠BCE=70°,
∴在△ABC中,∠BAC=180°﹣∠B﹣∠ACB=45°.
25.【解答】解:(1)根据题意得:
解得:.
(2)设购买A型车x台,B型车y台,根据题意得:
解得:
∴120×6+100×4=1120(万元)
答:购买这批混合动力公交车需要1120万元.
26.【解答】解:(1)设第一次购买时,甲类桌椅每套的购买价格为x元,乙类桌椅每套的购买价格为y元,
根据题意得:,
解得:,
答:第一次购买时,甲类桌椅每套的购买价格为150元,乙类桌椅每套的购买价格为210元;
(2)由题意得:甲类桌椅两次采购了9套,乙类采购了12套,
可容纳的总人数为3×9+5×12=87(人),
2,
答:该多功能数学实验室最多能同时容纳2个班级开展活动;
(3)若使用8张乙类桌子,则剩2名学生,甲类桌子坐不满,不合题意,
若使用7张乙类桌子,则剩7名学生,甲类桌子坐不满,不合题意,
若使用6张乙类桌子,则剩12名学生,甲类桌子正好坐满4张,符合题意,
答:应使用4张甲类桌子,6张乙类桌子.
第1页(共1页)
一.选择题(共12小题,满分36分,每小题3分)
1.(3分)下面四个手机APP图标中为轴对称图形的是( )
A. B. C. D.
2.(3分)要使分式有意义,则x的取值应该满足( )
A.x≠﹣5 B.x≠5 C.x=3 D.x≠0
3.(3分)下列计算正确的是( )
A.a2 a4=a6 B.(x﹣1)2=x2﹣1
C.3a2b﹣3ab2=0 D.(a2)5=a7
4.(3分)下列各数中,属于无理数的是( )
A. B.1.4141414 C. D.
5.(3分)不等式组的解集在数轴上表示正确的是( )
A.
B.
C.
D.
6.(3分)已知:等腰三角形两边长分别为9cm,5cm,则周长是( )
A.19cm B.23cm
C.19cm或23cm D.不能确定
7.(3分)如图,在3×3的正方形网格中有4个格点A,B,C,D,以其中一点为原点,网格线所在直线为坐标轴,建立直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称.则原点是( )
A.点A B.点B C.点C D.点D
8.(3分)若一个n边形的每个外角都相等,且它的一个外角等于45°,则n的值为( )
A.8 B.9 C.10 D.12
9.(3分)若(x+k)(x﹣5)的积中不含有x的一次项,则k的值是( )
A.0 B.﹣5或5 C.﹣5 D.5
10.(3分)如图,已知六边形ABCDEF的每个内角都是120°,且AB=1,BC=CD=7,DE=3,则这个六边形周长为( )
A.31 B.36 C.32 D.29
11.(3分)如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于D.如果∠A=30°,AE=6cm,那么CE等于( )
A. cm B.2 cm C.3 cm D.4 cm
12.(3分)如图,在△ABC中,AB=7,BC=4,AC=5,直线m是△ABC中BC边的垂直平分线,点P是直线m上的一动点.则△APC周长的最小值为( )
A.9 B.11 C.12 D.13
二.填空题(共6小题,满分18分,每小题3分)
13.(3分)已知1+x+x2=0,那么1+x+x2+x3+…+x2008+x2009+x2010的值是 .
14.(3分)从10边形的一个顶点出发可以引 条对角线.
15.(3分)重庆市作为“网红城市”,在2019年国庆节期间接待游客数量高达38590000人次,请将数字38590000用科学记数法表示为 .
16.(3分)若x,y为有理数,且|x+2|+(y﹣2)2=0,则()2021的值为 .
17.(3分)若x xa xb xc=x2015,则a+b+c= .
18.(3分)若按一定规律排列的数据如下:x,x2,x3,x4,x5,…,则第n个数可用代数式表示为 .(n为正整数)
三.(共8小题,满分61分)
19.(6分)化简求值:2a(a+b)﹣(a+b)2,其中a=3,b.
20.(7分)解分式方程:1.
21.(8分)如图,△ABC的三个顶点的坐标分别为A(﹣5,5)、B(﹣6,1)、C(﹣1,4),△ABC与△A1B1C1关于x轴对称,△A1B1C1与△A2B2C2关于y轴对称,点A1、B1、C1分别是点A、B、C的对应点,点A2、B2、C2分别是点A1、B1、C1的对应点.
(1)画出△A1B1C1与△A2B2C2;
(2)连接AC2、B1C2、AB1,求△AB1C2的面积.
22.(10分)现在购物时常用的支付方式有:A微信、B支付宝、C现金、D其他.某数学兴趣小组随机调查了某社区部分居民的常用支付方式,得到两幅不完整的统计图.
请你根据统计图提供的信息,解答下列问题:
(1)本次调查的居民总人数是 人,扇形统计图中“方式A”所对应的圆心角是 度,并补全条形统计图;
(2)若该社区有2600名居民,请估计使用A和B两种支付方式的居民共有多少名?
23.(8分)如图,在四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD∥BC.
(1)求证:四边形ABCD是平行四边形.
(2)若AC⊥BD,且AB=3,则平行四边形ABCD的周长为 .
24.(6分)如图,△ABC中,AD是高,CE是角平分线,AD交CE于点P,已知,∠APE=55°,∠AEP=100°,
求△ABC的各个内角的度数.
25.(8分)为了保护环境,某市公交公司决定购买一批共10台全新的混合动力公交车,现有A、B两种型号,其中每台的价格,年省油量如表:
A B
价格(万元/台) a b
节省的油量(万升/年 台) 2.4 2
经调查,购买一台A型车比购买一台B型车多20万元,购买2台A型车比购买3台B型车少60万元
(1)请求出a和b的值;
(2)若购买这批混合动力公交车每年能节省22.4万升汽油,求购买这批混合动力公交车需要多少万元?
26.(8分)某校准备购进21套桌椅来筹建一间多功能教学实验室,现有两类桌椅可供选择:甲类桌椅是三角形桌,每桌可坐3人,乙类桌椅是五边形桌,每桌可坐5人.学校分两次进行采购,第一次采购甲、乙两类桌椅均是原价;第二次采购时,甲因原材料上涨提价了20%,乙因促销活动降价20%.两次采购的数量和费用如下表:
购买甲类桌椅/套 购买乙类桌椅/套 购买总费用/元
第一次采购 6 5 1950
第二次采购 3 7 1716
(1)求第一次采购时,甲、乙类桌椅每套的购买价格.
(2)若该校每班有学生42人,问:该多功能教学实验室最多能同时容纳几个班级开展活动?
(3)某班42位同学需使用该实验室,管理员要求使用的桌椅每套必须坐满,请你计算桌椅的使用数量最少时,使用甲、乙类桌椅分别多少套.
2023-2024学年西藏昌都第二高级中学八年级(上)期末数学模拟试卷
参考答案与试题解析
一.选择题(共12小题,满分36分,每小题3分)
1.【解答】解:A、不是轴对称图形,不符合题意;
B、不是轴对称图形,是中心对称图形,不符合题意;
C、是轴对称图形,符合题意;
D、不是轴对称图形,不符合题意.
故选:C.
2.【解答】解:∵分式有意义,
∴x+5≠0,
解得x≠﹣5.
故选:A.
3.【解答】解:A、原式=a6,符合题意;
B、原式=x2﹣2x+1,不符合题意;
C、原式不能合并,不符合题意;
D、原式=a10,不符合题意.
故选:A.
4.【解答】解:A、是分数,属于有理数;
B、1.4141414是有限小数,属于有理数;
C、是无理数;
D、,是整数,属于有理数.
故选:C.
5.【解答】解:由3x﹣9<0,得:x<3,
由4x+6≤22,得:x≤4,
则不等式组的解集为x<3,
故选:A.
6.【解答】解:①若9cm是腰长,则三角形的三边分别为9cm、9cm、5cm,
能组成三角形,
周长=9+9+5=23cm,
②若9cm是底边长,则三角形的三边分别为9cm、5cm、5cm,
能组成三角形,
周长=9+5+5=19cm,
综上所述,三角形的周长为23cm或19cm.
故选:C.
7.【解答】解:如图:
以B为坐标原点建立坐标系,点A和点C关于y轴对称,
故选:B.
8.【解答】解:∵多边形的外角和为360°,一个外角45°,
∴多边形得到边数360÷45=8,所以是八边形.
故选:A.
9.【解答】解:(x+k)(x﹣5)=x2﹣5x+kx﹣5k=x2+(k﹣5)x﹣5k,
由积中不含x的一次项,得到k﹣5=0,
解得:k=5.
故选:D.
10.【解答】解:如图,延长并反向延长AB,CD,EF,
∵六边形ABCDEF的每个内角都是120°,
∴∠G=∠H=∠N=60°,
∴△GHN,△GBC,△AFH、△DEN都是等边三角形,
∴GN=CG+CD+DN=BC+CD+DE=7+7+3=17,
∴六边形ABCDEF的周长=GH+HN+NG﹣EN﹣AH﹣BG=3×17﹣3﹣9﹣7=32.
故选:C.
11.【解答】解:∵ED⊥AB,∠A=30°,
∴DEAE=3cm,
∵BE平分∠ABC,ED⊥AB,∠ACB=90°,
∴CE=DE=3cm,
故选:C.
12.【解答】解:∵直线m垂直平分BC,
∴B、C关于直线m对称,
设直线m交AB于D,
∴当P和D重合时,AP+CP的值最小,最小值等于AB的长,
∴△APC周长的最小值是7+5=12.
故选:C.
二.填空题(共6小题,满分18分,每小题3分)
13.【解答】解:1+x+x2+x3+…+x2010=1+(x+x2+x3)+(x4+x5+x6)+ +(x2008+x2009+x2010)
=1+x(1+x+x2)+x4(1+x+x2)+…+x2005(1+x+x2)+x2008(1+x+x2)
=1+x×0+…+x2008×0
=1+0+…+0
=1.
故答案为:1.
14.【解答】解:从10边形的一个顶点出发可引10﹣3=7条对角线,
故答案为:7.
15.【解答】解:3859 0000=3.859×107.
故答案为:3.859×107.
16.【解答】解:∵|x+2|+(y﹣2)2=0,|x+2|≥0,(y﹣2)2≥0,
∴x+2=0,y﹣2=0,
解得x=﹣2,y=2,
∴()2021=(﹣1)2021=﹣1.
故答案为:﹣1.
17.【解答】解:由x xa xb xc=1+a+b+c=x2015,得
a+b+c=2015﹣1=2014,
故答案为:2014.
18.【解答】解:∵一列数为:x,x2,x3,x4,x5,…,
∴第n个数可以表示为:(﹣1)n+1xn,
故答案为:(﹣1)n+1xn.
三.(共8小题,满分61分)
19.【解答】解:原式=2a2+2ab﹣(a2+2ab+b2)
=2a2+2ab﹣a2﹣2ab﹣b2
=a2﹣b2,
当a=3,b时,
原式=32﹣()2
=9
.
20.【解答】解:1,
方程两边都乘(x+2)(x﹣2),得3(x﹣2)+(x+2)(x﹣2)=(x+2)2,
解得:x=﹣14,
检验:当x=﹣14时,(x+2)(x﹣2)≠0,
所以x=﹣14是原方程的解,
即原方程的解是x=﹣14.
21.【解答】解:(1)如图所示,△A1B1C1和△A2B2C2即为所求,
(2)∵,
∴△AB1C2的面积是22.5.
22.【解答】解:(1)调查总人数:56÷28%=200(人),
使用“方式D”的人数:200×20%=40(人),
使用“方式A”的人数:200﹣40﹣56﹣44=60(人),
使用“方式A”所对应的圆心角为:360°108°,
故答案为:200,108,补全条形统计图如下:
(2)26001508(名),
答:该社区有2600名居民中使用A和B两种支付方式的大约有1508名.
23.【解答】(1)证明:∵AD∥BC,
∴∠ADO=∠CBO,
∵O是AC的中点,
∴OA=OC.
在△AOD和△COB中,,
∴△AOD≌△COB(AAS),
∴OD=OB.
∵OA=OC,
∴四边形ABCD是平行四边形;
(2)解:∵四边形ABCD是平行四边形,
又∵AC⊥BD,
∴四边形ABCD是菱形,
∴BC=CD=AD=AB=3,
∴四边形ABCD的周长=4AB=12;
故答案为:12.
24.【解答】解:在△AEP中,∠BAD=180°﹣∠APE﹣∠AEP=180°﹣55°﹣100°=25°,
∵AD是高,
∴∠ADB=∠ADC=90°,
∴∠B=180°﹣∠BAD﹣∠ADB=65°,
∴∠BCE=∠AEP﹣∠B=35°.
∵CE是角平分线,
∴∠ACB=2∠BCE=70°,
∴在△ABC中,∠BAC=180°﹣∠B﹣∠ACB=45°.
25.【解答】解:(1)根据题意得:
解得:.
(2)设购买A型车x台,B型车y台,根据题意得:
解得:
∴120×6+100×4=1120(万元)
答:购买这批混合动力公交车需要1120万元.
26.【解答】解:(1)设第一次购买时,甲类桌椅每套的购买价格为x元,乙类桌椅每套的购买价格为y元,
根据题意得:,
解得:,
答:第一次购买时,甲类桌椅每套的购买价格为150元,乙类桌椅每套的购买价格为210元;
(2)由题意得:甲类桌椅两次采购了9套,乙类采购了12套,
可容纳的总人数为3×9+5×12=87(人),
2,
答:该多功能数学实验室最多能同时容纳2个班级开展活动;
(3)若使用8张乙类桌子,则剩2名学生,甲类桌子坐不满,不合题意,
若使用7张乙类桌子,则剩7名学生,甲类桌子坐不满,不合题意,
若使用6张乙类桌子,则剩12名学生,甲类桌子正好坐满4张,符合题意,
答:应使用4张甲类桌子,6张乙类桌子.
第1页(共1页)
