2023-2024学年河南省驻马店市西平县九年级(上)期末数学模拟试卷(含解析)
文档属性
| 名称 | 2023-2024学年河南省驻马店市西平县九年级(上)期末数学模拟试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 361.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-30 01:40:40 | ||
图片预览

文档简介
2023-2024学年河南省驻马店市西平县九年级(上)期末数学模拟试卷
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
2.(3分)抛物线2的顶点坐标是( )
A. B. C. D.
3.(3分)关于抛物线y=﹣x2+2x﹣3的判断,下列说法正确的是( )
A.抛物线的开口方向向上
B.抛物线的对称轴是直线x=﹣1
C.当x<1时,y随x的增大而减小
D.抛物线与y轴的交点坐标为(0,﹣3)
4.(3分)一个不透明的袋子中装有30个红球和若干个白球,这些球除了颜色外都相同.若小明每次从袋子中随机摸出一个球,记下颜色后再放回,经过多次重复试验,小明发现摸到白球的频率逐渐稳定于0.4,则小明估计袋子中白球的个数约为( )
A.50个 B.30个 C.20个 D.12个
5.(3分)如图,△ABC中,DE∥BC,若AD:DB=2:3,则下列结论中正确的( )
A. B. C. D.
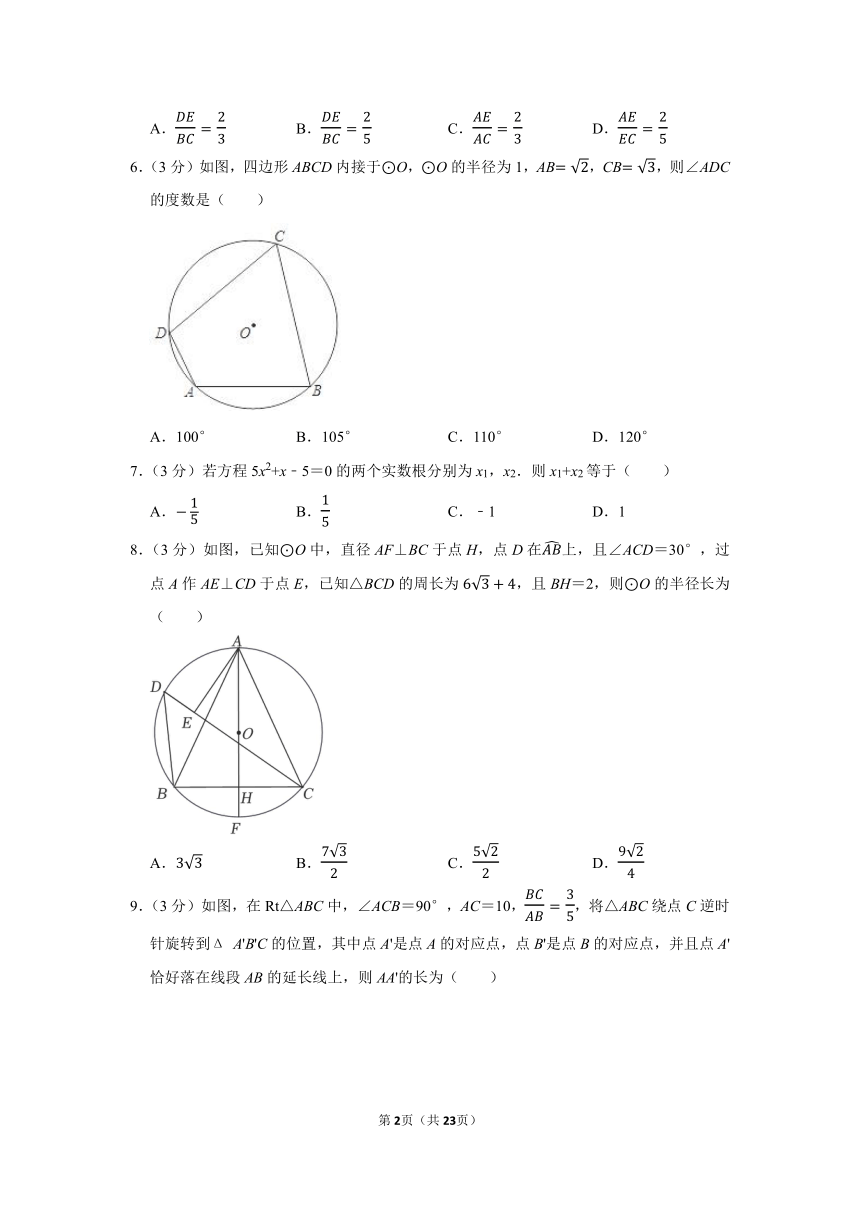
6.(3分)如图,四边形ABCD内接于⊙O,⊙O的半径为1,AB,CB,则∠ADC的度数是( )
A.100° B.105° C.110° D.120°
7.(3分)若方程5x2+x﹣5=0的两个实数根分别为x1,x2.则x1+x2等于( )
A. B. C.﹣1 D.1
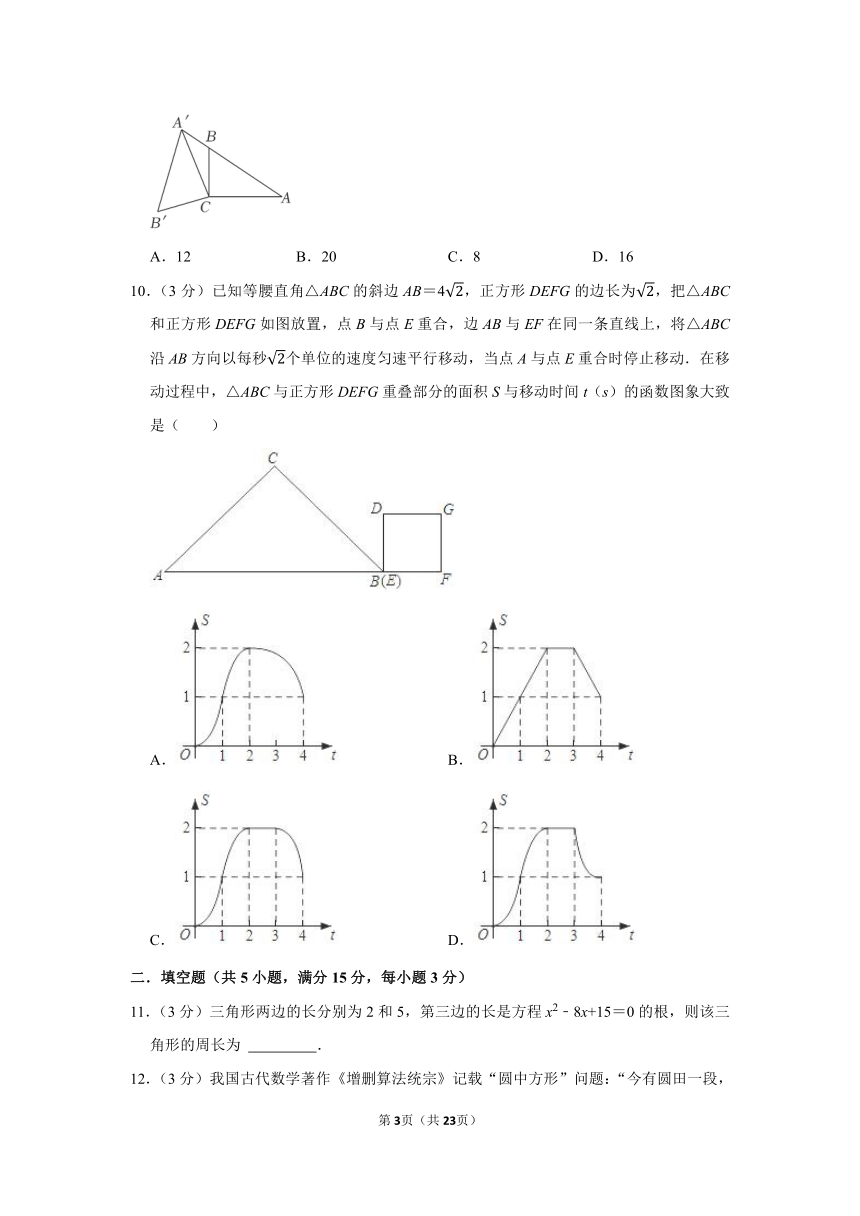
8.(3分)如图,已知⊙O中,直径AF⊥BC于点H,点D在上,且∠ACD=30°,过点A作AE⊥CD于点E,已知△BCD的周长为,且BH=2,则⊙O的半径长为( )
A. B. C. D.
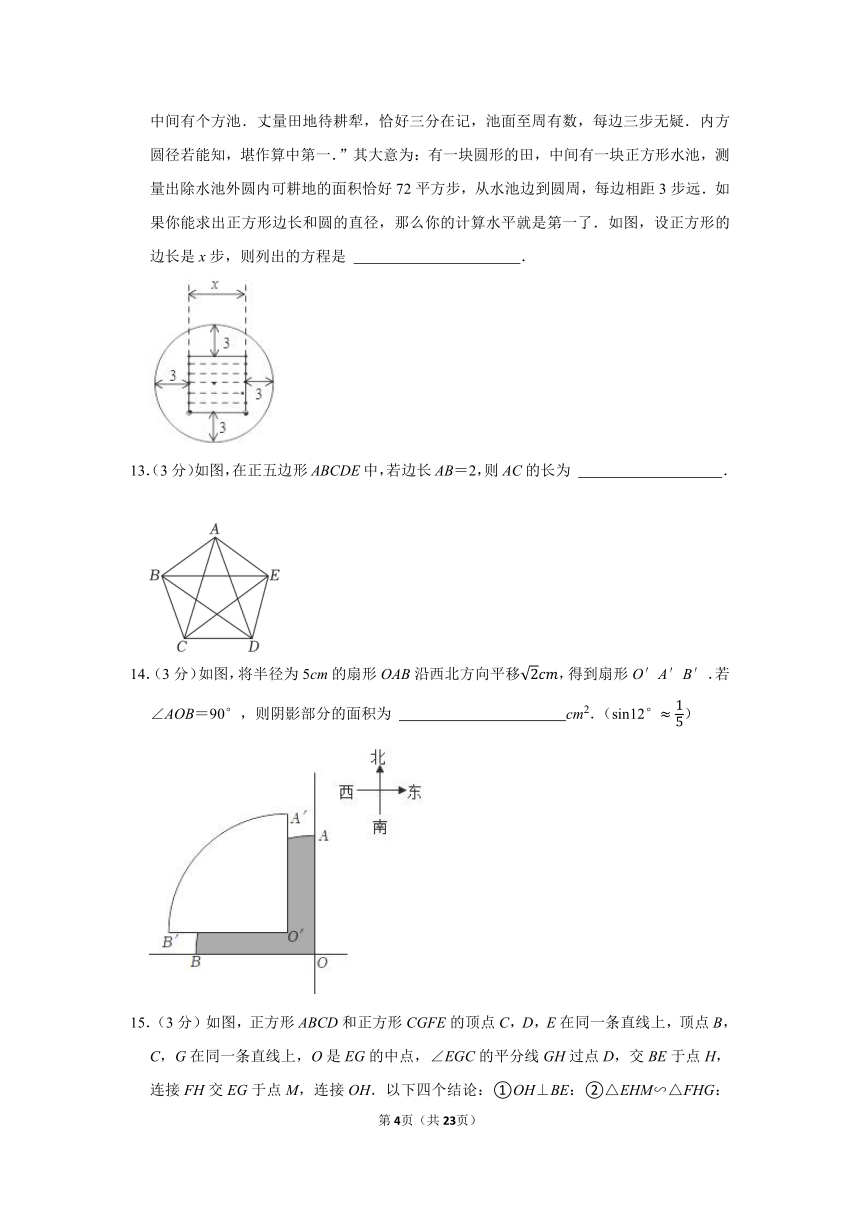
9.(3分)如图,在Rt△ABC中,∠ACB=90°,AC=10,,将△ABC绕点C逆时针旋转到Δ A'B'C的位置,其中点A'是点A的对应点,点B'是点B的对应点,并且点A'恰好落在线段AB的延长线上,则AA'的长为( )
A.12 B.20 C.8 D.16
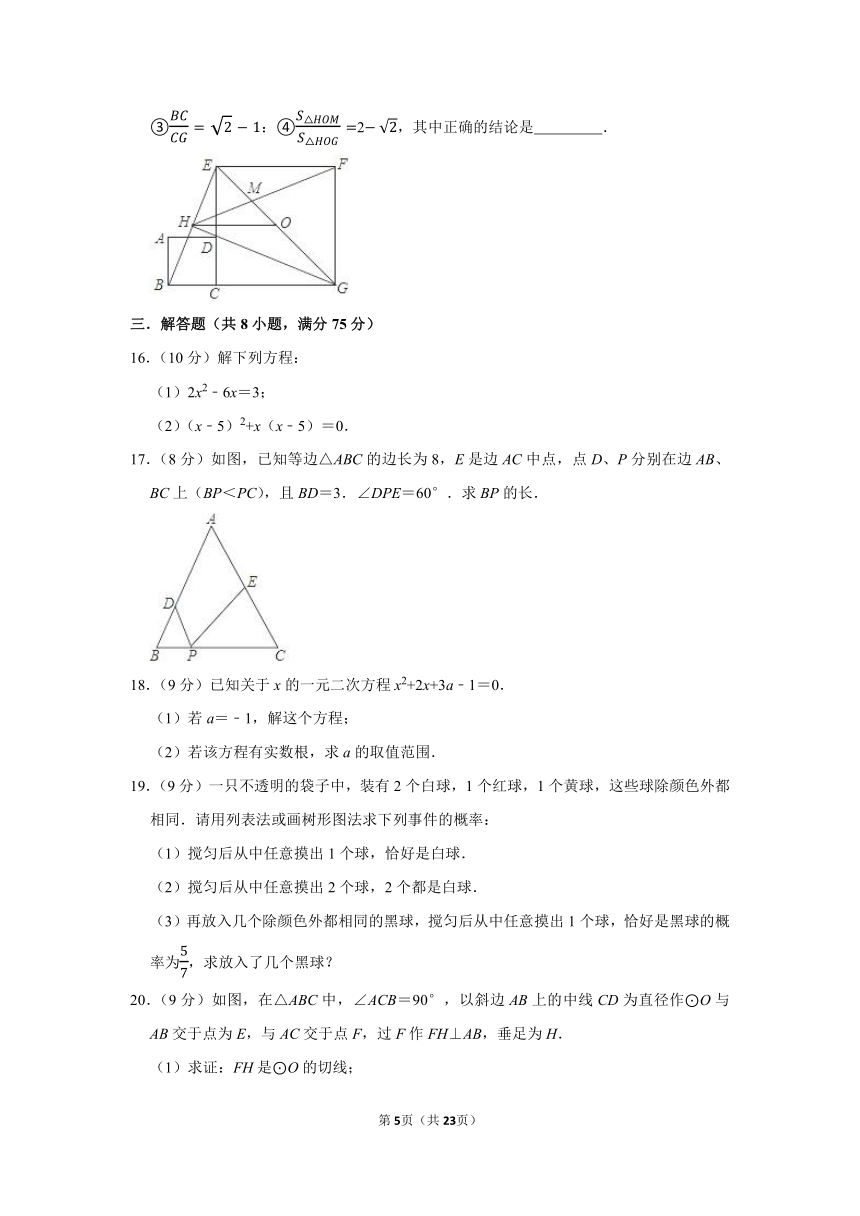
10.(3分)已知等腰直角△ABC的斜边AB=4,正方形DEFG的边长为,把△ABC和正方形DEFG如图放置,点B与点E重合,边AB与EF在同一条直线上,将△ABC沿AB方向以每秒个单位的速度匀速平行移动,当点A与点E重合时停止移动.在移动过程中,△ABC与正方形DEFG重叠部分的面积S与移动时间t(s)的函数图象大致是( )
A. B.
C. D.
二.填空题(共5小题,满分15分,每小题3分)
11.(3分)三角形两边的长分别为2和5,第三边的长是方程x2﹣8x+15=0的根,则该三角形的周长为 .
12.(3分)我国古代数学著作《增删算法统宗》记载“圆中方形”问题:“今有圆田一段,中间有个方池.丈量田地待耕犁,恰好三分在记,池面至周有数,每边三步无疑.内方圆径若能知,堪作算中第一.”其大意为:有一块圆形的田,中间有一块正方形水池,测量出除水池外圆内可耕地的面积恰好72平方步,从水池边到圆周,每边相距3步远.如果你能求出正方形边长和圆的直径,那么你的计算水平就是第一了.如图,设正方形的边长是x步,则列出的方程是 .
13.(3分)如图,在正五边形ABCDE中,若边长AB=2,则AC的长为 .
14.(3分)如图,将半径为5cm的扇形OAB沿西北方向平移,得到扇形O′A′B′.若∠AOB=90°,则阴影部分的面积为 cm2.(sin12°)
15.(3分)如图,正方形ABCD和正方形CGFE的顶点C,D,E在同一条直线上,顶点B,C,G在同一条直线上,O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接FH交EG于点M,连接OH.以下四个结论:①OH⊥BE:②△EHM∽△FHG:③:④2,其中正确的结论是 .
三.解答题(共8小题,满分75分)
16.(10分)解下列方程:
(1)2x2﹣6x=3;
(2)(x﹣5)2+x(x﹣5)=0.
17.(8分)如图,已知等边△ABC的边长为8,E是边AC中点,点D、P分别在边AB、BC上(BP<PC),且BD=3.∠DPE=60°.求BP的长.
18.(9分)已知关于x的一元二次方程x2+2x+3a﹣1=0.
(1)若a=﹣1,解这个方程;
(2)若该方程有实数根,求a的取值范围.
19.(9分)一只不透明的袋子中,装有2个白球,1个红球,1个黄球,这些球除颜色外都相同.请用列表法或画树形图法求下列事件的概率:
(1)搅匀后从中任意摸出1个球,恰好是白球.
(2)搅匀后从中任意摸出2个球,2个都是白球.
(3)再放入几个除颜色外都相同的黑球,搅匀后从中任意摸出1个球,恰好是黑球的概率为,求放入了几个黑球?
20.(9分)如图,在△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作⊙O与AB交于点为E,与AC交于点F,过F作FH⊥AB,垂足为H.
(1)求证:FH是⊙O的切线;
(2)若⊙O的半径为2.5,cosA,求AE的长.
21.(10分)某超市销售一款洗手液,这款洗手液成本价为每瓶16元,当销售单价定为每瓶20元时,每天可售出60瓶.市场调查反应:销售单价每上涨1元,则每天少售出5瓶.若设这款洗手液的销售单价上涨x元,每天的销售量利润为y元.
(1)每天的销售量为 瓶,每瓶洗手液的利润是 元;(用含x的代数式表示)
(2)若这款洗手液的日销售利润y达到300元,则销售单价应上涨多少元?
(3)当销售单价上涨多少元时,这款洗手液每天的销售利润y最大,最大利润为多少元?
22.(10分)如图,在平面直角坐标系xOy中,已知抛物线y=ax2﹣2ax+c(a>0)与x轴交于点A(﹣2,0)、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,直线经过点A,交抛物线的对称轴于点E.
(1)求△ABE的面积;
(2)联结EC,交x轴于点F,联结AC,若,求抛物线的表达式;
(3)在(2)的条件下,点P是直线AE上一点,且∠EPB=∠ECB,求点P的坐标.
23.(10分)如图,在△ABC中,AB=AC,∠BAC=α,点D在BC边上,以点A为中心,将线段AD顺时针旋转α得到线段AE,连接BE.
(1)求证:BA平分∠EBC;
(2)连接DE交AB于点F,过点C作CG∥AB,交ED的延长线于点G.补全图形,用等式表示线段EF与DG之间的数量关系,并证明.
2023-2024学年河南省驻马店市西平县九年级(上)期末数学模拟试卷
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.【解答】解:A.该图形是轴对称图形,不是中心对称图形,故本选项不符合题意;
B.该图形既是轴对称图形又是中心对称图形,故选项符合题意;
C.该图形是轴对称图形,不是中心对称图形,故本选项不符合题意;
D.该图形不是轴对称图形,是中心对称图形,故本选项不符合题意.
故选:B.
2.【解答】解:∵抛物线2,
∴抛物线2的顶点坐标是:(,2),
故选:A.
3.【解答】解:∵抛物线y=﹣x2+2x﹣3=﹣(x﹣1)2﹣2,
∴该抛物线的开口向下,抛物线的对称轴是直线x=1,当x<1时,y随x的增大而增大,故选项A、B、C不符合题意;
∵当x=0时,y=﹣3,
∴抛物线与y轴的交点坐标为(0,﹣3),故选项D符合题意.
故选:D.
4.【解答】解:设袋中白球有x个,
根据题意,得:0.4,
解得:x=32,
经检验:x=20是分式方程的解,
所以估计袋子中白球的个数约为20个,
故选:C.
5.【解答】解:∵AD:DB=2:3,
∴,
∵DE∥BC,
∴,A错误,B正确;
,C错误;
,D错误.
故选:B.
6.【解答】解:过O分别作OE⊥AB于E,OF⊥BC于F,连接OB,
则AE=BEAB,BF=CFBC,OB=1
∴cos∠OBE,cos∠OBF,
∴∠OBE=45°,∠OBF=30°,
∴∠ABC=∠OBE+∠OBF=75°,
∵四边形ABCD内接于⊙O,
∴∠ADC+∠ABC=180°,
∴∠ADC=180°﹣75°=105°,
故选:B.
7.【解答】解:根据根与系数的关系得,x1+x2.
故选:A.
8.【解答】解:如图,
设AF与CD交于点G,延长CD至T,使DT=BD,连接BG,AT,BT,OC,
∴∠DBT=∠DTB,
∵,
∴∠BDC=∠BAC,
∵直径AF⊥BC,
∴CH=BH=2,
∴AB=AC,GB=GC,
∴∠BAH=∠CAH∠BAC,∠ABC=∠ACB,∠GBC=∠GCB,
∴∠ABC﹣∠GBC=∠ACB﹣∠GCB,
∴∠ABG=∠ACG=30°,
∵∠BDC=∠DTB+∠DBT=2∠BTD,
∴∠BTD=∠BAH,
∴点T、B、G、A共圆,
∴∠ATG=∠ABG=30°,
∴∠ATG=∠ABE=30°,
∴AC=AT,
∵AE⊥CD,
∴CE=ETCT,
∵△BCD的周长为,BC=4,
∴CD+BD=6,
∴CT=TD+CD=6,
∴CE=3,
在Rt△ACE中,∠ABE=30°,CE=3,
∴AC6,
∴AH4,
设OA=OC=r,则OH=AH﹣OA=4r,
∵OC2﹣OH2=CH2,
∴r2﹣(4r)2=22,
∴r,
故选:D.
9.【解答】解:过点C作CD⊥AB于点D,
∵AC=10,,
设BC=3x,AB=5x,
∴AC=4x=10,
∴x,
∴BC,AB,
∵S△ABCAB CD,
∴CD6,
∴AD8,
∵将△ABC绕点C逆时针旋转到Δ A'B'C的位置,
∴CA=CA',
∵CD⊥AA',
∴AA'=2AD=16.
故选:D.
10.【解答】解:①当0<t≤1时,St2,函数为开口方向向上的抛物线;
②当1<t≤2时,如图2,
设BC交FG于H,则FH=BF,
则GHBF,
S=S正方形DEFG﹣S△HMGt2+4t﹣2,函数为开口方向向下的抛物线;
③当2<t≤3时,S=2;
④当3<t≤4时,同理可得St2+6t﹣7,函数为开口方向向下的抛物线;
故只有选项C符合题意.
故选:C.
二.填空题(共5小题,满分15分,每小题3分)
11.【解答】解:解方程x2﹣8x+15=0得:x=3或5,
当第三边为3时,2+3=5,不符合三角形三边关系定理,不能组成三角形,舍去;
当第三边为5时,符合三角形三边关系定理,能组成三角形,此时三角形的周长是2+5+5=12,
故答案为:12.
12.【解答】解:设正方形的边长是x步,则列出的方程是:π(3)2﹣x2=72.
故答案为:π(3)2﹣x2=72.
13.【解答】解:如图,∵五边形ABCDE是正五边形,
∴∠ABC=∠BCD108°,AB=BC=CD=2,
∴∠BCA=∠BAC36°,
∴∠ABF=108°﹣36°=72°,
∵∠AFB=∠CBD+∠BCA=36°+36°=72°,
∴∠ABF=∠AFB,
∴AF=AB=2,
∵∠BCF=∠ACB,∠BAC∠CBF,
∴△BCF∽△ACB,
∴,
即,
解得CF1(取正值),
∴AC=CF+AF1+21,
故答案为:1.
14.【解答】解:如图,设O′A′交于点D,O′B′交于点E,连接OE,OD,过点D作DJ⊥OA于点J.
将半径为5cm的扇形OAB沿西北方向平移,即将半径为5cm的扇形OAB向西平移1cm,再向上平移1cm,
∴O′E=EC﹣O′C1=21,
∵sin∠AOD,
∴∠AOD=∠BOE=12°,
∴S阴=S扇形BOE+S扇形AOD+S△OO′E+S△OO′D
=221×(21)
=(21)(cm2).
故答案为:(21).
15.【解答】解:如图,∵四边形ABCD和四边形CGFE是正方形,
∴BC=CD,CE=CG,∠BCE=∠DCG,
在△BCE和△DCG中,
,
∴△BCE≌△DCG(SAS),
∴∠BEC=∠BGH,
∵∠BGH+∠CDG=90°,∠CDG=∠HDE,
∴∠BEC+∠HDE=90°,
∴GH⊥BE.
故①错误;
∵△EHG是直角三角形,O为EG的中点,
∴OH=OG=OE,
∴点H在正方形CGFE的外接圆上,
∵EF=FG,
∴∠FHG=∠EHF=∠EGF=45°,∠HEG=∠HFG,
∴△EHM∽△FHG,
故②正确;
∵△BGH≌△EGH,
∴BH=EH,
又∵O是EG的中点,
∴HO∥BG,
∴△DHN∽△DGC,
∴,
设EC和OH相交于点N.
设HN=a,则BC=2a,设正方形ECGF的边长是2b,则NC=b,CD=2a,
∴,即a2+2ab﹣b2=0,
解得:a=(﹣1)b,或a=(﹣1)b(舍去),
则1,
∴1,
故③正确;
∵△BGH≌△EGH,
∴EG=BG,
∵HO是△EBG的中位线,
∴HOBG,
∴HOEG,
设正方形ECGF的边长是2b,
∴EG=2b,
∴HOb,
∵OH∥BG,CG∥EF,
∴OH∥EF,
∴△MHO∽△MFE,
∴,
∴EMOM,
∴1,
∴1,
∵EO=GO,
∴S△HOE=S△HOG,
∴1.
故④错误.
故其中正确的结论是②③.
故答案为:②③.
三.解答题(共8小题,满分75分)
16.【解答】解:(1)∵2x2﹣6x=3,
∴x2﹣3x,
则x2﹣3x,即(x)2,
∴x±,
∴x1,x2;
(2)∵(x﹣5)2+x(x﹣5)=0,
∴(x﹣5)(2x﹣5)=0,
则x﹣5=0或2x﹣5=0,
解得x1=5,x2.
17.【解答】解:∵△ABC是等边三角形,
∴AB=BC=AC=8,∠B=∠C=60°,
∵E是边AC中点,
∴CE=4,
∵∠DPC=∠B+∠BDP=∠DPE+∠EPC,且∠DPE=60°,
∴∠BDP=∠EPC,且∠B=∠C,
∴△BDP∽△CPE,
∴,
∴3×4=BP(8﹣BP)
∴BP=2或6,
∵BP<PC,
∴BP=2.
18.【解答】解:(1)当a=﹣1时,方程为x2+2x﹣4=0,
解得x1=﹣1,x2=﹣1;
(2)由题意得,Δ=22﹣4(3a﹣1)=﹣12a+8≥0,
∴a.
故a的取值范围为a.
19.【解答】解:(1)将“恰好是白球”记为事件A,
则P(A).
(2)画树状图如图所示:共有12个等可能的结果,
从中任意摸出2个球,“2个都是白球”记为事件B,
则P(B).
(3)设放入n个黑球,由题意得,
解得n=10,即放入了10个黑球.
20.【解答】(1)证明:连接OF,DF,
∵∠ACB=90°,CD是斜边AB上的中线,FH⊥AB,
∴CD=ADAB,∠AHF=90°,
∵CD是⊙O直径,
∴DF⊥AC,
∴F是AC的中点,
∴OF是△ADC的中位线,
∴OF∥AD,
∴∠OFH=∠AHF=90°,
∴OF⊥FH,
∵OF是⊙O的半径,
∴FH是⊙O的切线;
(2)解:连接CE,则∠AEC=90°,
由⊙O的半径为2.5,知CD=AD=5,
由(1)知,DF⊥AC,F是AC的中点,
在Rt△AFD中,cosA,
∴AF=4,
∴AC=8,
在Rt△AEC中,cosA,
∴AE.
21.【解答】解:(1)每天的销售量为(60﹣5x)瓶,每瓶洗手液的利润是(4+x)元;
故答案为:(60﹣5x);(4+x);
(2)根据题意得,(60﹣5x)(4+x)=300,
解得:x1=6,x2=2,
答:销售单价应上涨2元或6元;
(3)根据题意得,y=(60﹣5x)(4+x)=﹣5(x﹣12)(x+4)=﹣5(x﹣4)2+320,
答:当销售单价上涨4元时,这款洗手液每天的销售利润y最大,最大利润为320元.
22.【解答】解:(1)将A(﹣2,0)代入yx+b得:
﹣1+b=0,
解得b=1,
∴yx+1,
抛物线y=ax2﹣2ax+c的对称轴为直线x1,
在yx+1中,令x=1得y,
∴E(1,),
∵抛物线y=ax2﹣2ax+c(a>0)与x轴交于点A(﹣2,0)、B两点,
∴A(﹣2,0),B关于对称轴直线x=1对称,
∴B(4,0),
∴AB=6,
∴S△ABEAB |yE|6,
答:△ABE的面积是;
(2)过E作EK⊥y轴于K,如图:
∵,
∴,
∵OF∥EK,
∴,
由(1)知E(1,),
∴OK,
∴OC=2,
∴C(0,﹣2),
把A(﹣2,0),C(0,﹣2)代入y=ax2﹣2ax+c得:
,
解得,
∴抛物线的表达式为yx2x﹣2;
(3)过B作BP∥CE交直线AE于P,以B为圆心,BP为半径作圆与直线AE另一交点为P',如图:
由(1)(2)知直线AE为yx+1,C(0,﹣2),B(4,0),
设直线BC为y=tx﹣2,将B(4,0)代入得:
4t﹣2=0,
解得t,
∴直线BC为yx﹣2,
∴AE∥BC,
∵BP∥CE,
∴四边形ECBP是平行四边形,
∴∠ECB=∠EPB,
∴P是满足题意的点,
由C(0,﹣2)平移至B(4,0)与E(1,)平移至P方式相同,可得P(5,),
∵BP=BP',
∴∠EP'B=∠EPB=∠ECB,
∴P'是满足题意的点,
设P'(m,m+1),
∵BP=BP',
∴(5﹣4)2+(0)2=(m﹣4)2+(m+1)2,
解得m=5(与P重合,舍去)或m,
∴P'(,),
综上所述,点P的坐标为(5,)或(,).
23.【解答】(1)证明:∵∠DAE=∠BAC=α,
∴∠DAE﹣∠BAD=∠BAC﹣∠BAD,
即∠BAE=∠CAD,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(SAS),
∴∠ABE=∠ACD,
∵AB=AC,
∴∠ABC=∠ACD,
∴∠ABC=∠ABE,
∴BA平分∠EBC;
(2)解:EF=DG,
证明:如图,在AC上截取AH=AF,连接DH,在CG延长线时取点I,使CI=CH,连接DI,
在△AEF和△ADH中,
,
∴△AEF≌△ADH(SAS),
∴EF=DH,∠AFE=∠AHD,
∴∠AFD=∠CHD,
∵CG∥AB,
∴∠AFD=∠DGI,
∴∠DGI=∠CHD,
∵AB=AC,
∴∠ABC=∠ACD,
∵CG∥AB,
∴∠ABC=∠ICD,
∴∠ACD=∠ICD,
在△HCD和△ICD中,
,
∴△HCD≌△ICD(SAS),
∴∠CID=∠CHD,DI=DH,
∵∠DGI=∠CHD,
∴∠CID=∠DGI,
∴DI=DG,
∴DG=DH,
∵EF=DH,
∴EF=DG.
第1页(共1页)
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
2.(3分)抛物线2的顶点坐标是( )
A. B. C. D.
3.(3分)关于抛物线y=﹣x2+2x﹣3的判断,下列说法正确的是( )
A.抛物线的开口方向向上
B.抛物线的对称轴是直线x=﹣1
C.当x<1时,y随x的增大而减小
D.抛物线与y轴的交点坐标为(0,﹣3)
4.(3分)一个不透明的袋子中装有30个红球和若干个白球,这些球除了颜色外都相同.若小明每次从袋子中随机摸出一个球,记下颜色后再放回,经过多次重复试验,小明发现摸到白球的频率逐渐稳定于0.4,则小明估计袋子中白球的个数约为( )
A.50个 B.30个 C.20个 D.12个
5.(3分)如图,△ABC中,DE∥BC,若AD:DB=2:3,则下列结论中正确的( )
A. B. C. D.
6.(3分)如图,四边形ABCD内接于⊙O,⊙O的半径为1,AB,CB,则∠ADC的度数是( )
A.100° B.105° C.110° D.120°
7.(3分)若方程5x2+x﹣5=0的两个实数根分别为x1,x2.则x1+x2等于( )
A. B. C.﹣1 D.1
8.(3分)如图,已知⊙O中,直径AF⊥BC于点H,点D在上,且∠ACD=30°,过点A作AE⊥CD于点E,已知△BCD的周长为,且BH=2,则⊙O的半径长为( )
A. B. C. D.
9.(3分)如图,在Rt△ABC中,∠ACB=90°,AC=10,,将△ABC绕点C逆时针旋转到Δ A'B'C的位置,其中点A'是点A的对应点,点B'是点B的对应点,并且点A'恰好落在线段AB的延长线上,则AA'的长为( )
A.12 B.20 C.8 D.16
10.(3分)已知等腰直角△ABC的斜边AB=4,正方形DEFG的边长为,把△ABC和正方形DEFG如图放置,点B与点E重合,边AB与EF在同一条直线上,将△ABC沿AB方向以每秒个单位的速度匀速平行移动,当点A与点E重合时停止移动.在移动过程中,△ABC与正方形DEFG重叠部分的面积S与移动时间t(s)的函数图象大致是( )
A. B.
C. D.
二.填空题(共5小题,满分15分,每小题3分)
11.(3分)三角形两边的长分别为2和5,第三边的长是方程x2﹣8x+15=0的根,则该三角形的周长为 .
12.(3分)我国古代数学著作《增删算法统宗》记载“圆中方形”问题:“今有圆田一段,中间有个方池.丈量田地待耕犁,恰好三分在记,池面至周有数,每边三步无疑.内方圆径若能知,堪作算中第一.”其大意为:有一块圆形的田,中间有一块正方形水池,测量出除水池外圆内可耕地的面积恰好72平方步,从水池边到圆周,每边相距3步远.如果你能求出正方形边长和圆的直径,那么你的计算水平就是第一了.如图,设正方形的边长是x步,则列出的方程是 .
13.(3分)如图,在正五边形ABCDE中,若边长AB=2,则AC的长为 .
14.(3分)如图,将半径为5cm的扇形OAB沿西北方向平移,得到扇形O′A′B′.若∠AOB=90°,则阴影部分的面积为 cm2.(sin12°)
15.(3分)如图,正方形ABCD和正方形CGFE的顶点C,D,E在同一条直线上,顶点B,C,G在同一条直线上,O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接FH交EG于点M,连接OH.以下四个结论:①OH⊥BE:②△EHM∽△FHG:③:④2,其中正确的结论是 .
三.解答题(共8小题,满分75分)
16.(10分)解下列方程:
(1)2x2﹣6x=3;
(2)(x﹣5)2+x(x﹣5)=0.
17.(8分)如图,已知等边△ABC的边长为8,E是边AC中点,点D、P分别在边AB、BC上(BP<PC),且BD=3.∠DPE=60°.求BP的长.
18.(9分)已知关于x的一元二次方程x2+2x+3a﹣1=0.
(1)若a=﹣1,解这个方程;
(2)若该方程有实数根,求a的取值范围.
19.(9分)一只不透明的袋子中,装有2个白球,1个红球,1个黄球,这些球除颜色外都相同.请用列表法或画树形图法求下列事件的概率:
(1)搅匀后从中任意摸出1个球,恰好是白球.
(2)搅匀后从中任意摸出2个球,2个都是白球.
(3)再放入几个除颜色外都相同的黑球,搅匀后从中任意摸出1个球,恰好是黑球的概率为,求放入了几个黑球?
20.(9分)如图,在△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作⊙O与AB交于点为E,与AC交于点F,过F作FH⊥AB,垂足为H.
(1)求证:FH是⊙O的切线;
(2)若⊙O的半径为2.5,cosA,求AE的长.
21.(10分)某超市销售一款洗手液,这款洗手液成本价为每瓶16元,当销售单价定为每瓶20元时,每天可售出60瓶.市场调查反应:销售单价每上涨1元,则每天少售出5瓶.若设这款洗手液的销售单价上涨x元,每天的销售量利润为y元.
(1)每天的销售量为 瓶,每瓶洗手液的利润是 元;(用含x的代数式表示)
(2)若这款洗手液的日销售利润y达到300元,则销售单价应上涨多少元?
(3)当销售单价上涨多少元时,这款洗手液每天的销售利润y最大,最大利润为多少元?
22.(10分)如图,在平面直角坐标系xOy中,已知抛物线y=ax2﹣2ax+c(a>0)与x轴交于点A(﹣2,0)、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,直线经过点A,交抛物线的对称轴于点E.
(1)求△ABE的面积;
(2)联结EC,交x轴于点F,联结AC,若,求抛物线的表达式;
(3)在(2)的条件下,点P是直线AE上一点,且∠EPB=∠ECB,求点P的坐标.
23.(10分)如图,在△ABC中,AB=AC,∠BAC=α,点D在BC边上,以点A为中心,将线段AD顺时针旋转α得到线段AE,连接BE.
(1)求证:BA平分∠EBC;
(2)连接DE交AB于点F,过点C作CG∥AB,交ED的延长线于点G.补全图形,用等式表示线段EF与DG之间的数量关系,并证明.
2023-2024学年河南省驻马店市西平县九年级(上)期末数学模拟试卷
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.【解答】解:A.该图形是轴对称图形,不是中心对称图形,故本选项不符合题意;
B.该图形既是轴对称图形又是中心对称图形,故选项符合题意;
C.该图形是轴对称图形,不是中心对称图形,故本选项不符合题意;
D.该图形不是轴对称图形,是中心对称图形,故本选项不符合题意.
故选:B.
2.【解答】解:∵抛物线2,
∴抛物线2的顶点坐标是:(,2),
故选:A.
3.【解答】解:∵抛物线y=﹣x2+2x﹣3=﹣(x﹣1)2﹣2,
∴该抛物线的开口向下,抛物线的对称轴是直线x=1,当x<1时,y随x的增大而增大,故选项A、B、C不符合题意;
∵当x=0时,y=﹣3,
∴抛物线与y轴的交点坐标为(0,﹣3),故选项D符合题意.
故选:D.
4.【解答】解:设袋中白球有x个,
根据题意,得:0.4,
解得:x=32,
经检验:x=20是分式方程的解,
所以估计袋子中白球的个数约为20个,
故选:C.
5.【解答】解:∵AD:DB=2:3,
∴,
∵DE∥BC,
∴,A错误,B正确;
,C错误;
,D错误.
故选:B.
6.【解答】解:过O分别作OE⊥AB于E,OF⊥BC于F,连接OB,
则AE=BEAB,BF=CFBC,OB=1
∴cos∠OBE,cos∠OBF,
∴∠OBE=45°,∠OBF=30°,
∴∠ABC=∠OBE+∠OBF=75°,
∵四边形ABCD内接于⊙O,
∴∠ADC+∠ABC=180°,
∴∠ADC=180°﹣75°=105°,
故选:B.
7.【解答】解:根据根与系数的关系得,x1+x2.
故选:A.
8.【解答】解:如图,
设AF与CD交于点G,延长CD至T,使DT=BD,连接BG,AT,BT,OC,
∴∠DBT=∠DTB,
∵,
∴∠BDC=∠BAC,
∵直径AF⊥BC,
∴CH=BH=2,
∴AB=AC,GB=GC,
∴∠BAH=∠CAH∠BAC,∠ABC=∠ACB,∠GBC=∠GCB,
∴∠ABC﹣∠GBC=∠ACB﹣∠GCB,
∴∠ABG=∠ACG=30°,
∵∠BDC=∠DTB+∠DBT=2∠BTD,
∴∠BTD=∠BAH,
∴点T、B、G、A共圆,
∴∠ATG=∠ABG=30°,
∴∠ATG=∠ABE=30°,
∴AC=AT,
∵AE⊥CD,
∴CE=ETCT,
∵△BCD的周长为,BC=4,
∴CD+BD=6,
∴CT=TD+CD=6,
∴CE=3,
在Rt△ACE中,∠ABE=30°,CE=3,
∴AC6,
∴AH4,
设OA=OC=r,则OH=AH﹣OA=4r,
∵OC2﹣OH2=CH2,
∴r2﹣(4r)2=22,
∴r,
故选:D.
9.【解答】解:过点C作CD⊥AB于点D,
∵AC=10,,
设BC=3x,AB=5x,
∴AC=4x=10,
∴x,
∴BC,AB,
∵S△ABCAB CD,
∴CD6,
∴AD8,
∵将△ABC绕点C逆时针旋转到Δ A'B'C的位置,
∴CA=CA',
∵CD⊥AA',
∴AA'=2AD=16.
故选:D.
10.【解答】解:①当0<t≤1时,St2,函数为开口方向向上的抛物线;
②当1<t≤2时,如图2,
设BC交FG于H,则FH=BF,
则GHBF,
S=S正方形DEFG﹣S△HMGt2+4t﹣2,函数为开口方向向下的抛物线;
③当2<t≤3时,S=2;
④当3<t≤4时,同理可得St2+6t﹣7,函数为开口方向向下的抛物线;
故只有选项C符合题意.
故选:C.
二.填空题(共5小题,满分15分,每小题3分)
11.【解答】解:解方程x2﹣8x+15=0得:x=3或5,
当第三边为3时,2+3=5,不符合三角形三边关系定理,不能组成三角形,舍去;
当第三边为5时,符合三角形三边关系定理,能组成三角形,此时三角形的周长是2+5+5=12,
故答案为:12.
12.【解答】解:设正方形的边长是x步,则列出的方程是:π(3)2﹣x2=72.
故答案为:π(3)2﹣x2=72.
13.【解答】解:如图,∵五边形ABCDE是正五边形,
∴∠ABC=∠BCD108°,AB=BC=CD=2,
∴∠BCA=∠BAC36°,
∴∠ABF=108°﹣36°=72°,
∵∠AFB=∠CBD+∠BCA=36°+36°=72°,
∴∠ABF=∠AFB,
∴AF=AB=2,
∵∠BCF=∠ACB,∠BAC∠CBF,
∴△BCF∽△ACB,
∴,
即,
解得CF1(取正值),
∴AC=CF+AF1+21,
故答案为:1.
14.【解答】解:如图,设O′A′交于点D,O′B′交于点E,连接OE,OD,过点D作DJ⊥OA于点J.
将半径为5cm的扇形OAB沿西北方向平移,即将半径为5cm的扇形OAB向西平移1cm,再向上平移1cm,
∴O′E=EC﹣O′C1=21,
∵sin∠AOD,
∴∠AOD=∠BOE=12°,
∴S阴=S扇形BOE+S扇形AOD+S△OO′E+S△OO′D
=221×(21)
=(21)(cm2).
故答案为:(21).
15.【解答】解:如图,∵四边形ABCD和四边形CGFE是正方形,
∴BC=CD,CE=CG,∠BCE=∠DCG,
在△BCE和△DCG中,
,
∴△BCE≌△DCG(SAS),
∴∠BEC=∠BGH,
∵∠BGH+∠CDG=90°,∠CDG=∠HDE,
∴∠BEC+∠HDE=90°,
∴GH⊥BE.
故①错误;
∵△EHG是直角三角形,O为EG的中点,
∴OH=OG=OE,
∴点H在正方形CGFE的外接圆上,
∵EF=FG,
∴∠FHG=∠EHF=∠EGF=45°,∠HEG=∠HFG,
∴△EHM∽△FHG,
故②正确;
∵△BGH≌△EGH,
∴BH=EH,
又∵O是EG的中点,
∴HO∥BG,
∴△DHN∽△DGC,
∴,
设EC和OH相交于点N.
设HN=a,则BC=2a,设正方形ECGF的边长是2b,则NC=b,CD=2a,
∴,即a2+2ab﹣b2=0,
解得:a=(﹣1)b,或a=(﹣1)b(舍去),
则1,
∴1,
故③正确;
∵△BGH≌△EGH,
∴EG=BG,
∵HO是△EBG的中位线,
∴HOBG,
∴HOEG,
设正方形ECGF的边长是2b,
∴EG=2b,
∴HOb,
∵OH∥BG,CG∥EF,
∴OH∥EF,
∴△MHO∽△MFE,
∴,
∴EMOM,
∴1,
∴1,
∵EO=GO,
∴S△HOE=S△HOG,
∴1.
故④错误.
故其中正确的结论是②③.
故答案为:②③.
三.解答题(共8小题,满分75分)
16.【解答】解:(1)∵2x2﹣6x=3,
∴x2﹣3x,
则x2﹣3x,即(x)2,
∴x±,
∴x1,x2;
(2)∵(x﹣5)2+x(x﹣5)=0,
∴(x﹣5)(2x﹣5)=0,
则x﹣5=0或2x﹣5=0,
解得x1=5,x2.
17.【解答】解:∵△ABC是等边三角形,
∴AB=BC=AC=8,∠B=∠C=60°,
∵E是边AC中点,
∴CE=4,
∵∠DPC=∠B+∠BDP=∠DPE+∠EPC,且∠DPE=60°,
∴∠BDP=∠EPC,且∠B=∠C,
∴△BDP∽△CPE,
∴,
∴3×4=BP(8﹣BP)
∴BP=2或6,
∵BP<PC,
∴BP=2.
18.【解答】解:(1)当a=﹣1时,方程为x2+2x﹣4=0,
解得x1=﹣1,x2=﹣1;
(2)由题意得,Δ=22﹣4(3a﹣1)=﹣12a+8≥0,
∴a.
故a的取值范围为a.
19.【解答】解:(1)将“恰好是白球”记为事件A,
则P(A).
(2)画树状图如图所示:共有12个等可能的结果,
从中任意摸出2个球,“2个都是白球”记为事件B,
则P(B).
(3)设放入n个黑球,由题意得,
解得n=10,即放入了10个黑球.
20.【解答】(1)证明:连接OF,DF,
∵∠ACB=90°,CD是斜边AB上的中线,FH⊥AB,
∴CD=ADAB,∠AHF=90°,
∵CD是⊙O直径,
∴DF⊥AC,
∴F是AC的中点,
∴OF是△ADC的中位线,
∴OF∥AD,
∴∠OFH=∠AHF=90°,
∴OF⊥FH,
∵OF是⊙O的半径,
∴FH是⊙O的切线;
(2)解:连接CE,则∠AEC=90°,
由⊙O的半径为2.5,知CD=AD=5,
由(1)知,DF⊥AC,F是AC的中点,
在Rt△AFD中,cosA,
∴AF=4,
∴AC=8,
在Rt△AEC中,cosA,
∴AE.
21.【解答】解:(1)每天的销售量为(60﹣5x)瓶,每瓶洗手液的利润是(4+x)元;
故答案为:(60﹣5x);(4+x);
(2)根据题意得,(60﹣5x)(4+x)=300,
解得:x1=6,x2=2,
答:销售单价应上涨2元或6元;
(3)根据题意得,y=(60﹣5x)(4+x)=﹣5(x﹣12)(x+4)=﹣5(x﹣4)2+320,
答:当销售单价上涨4元时,这款洗手液每天的销售利润y最大,最大利润为320元.
22.【解答】解:(1)将A(﹣2,0)代入yx+b得:
﹣1+b=0,
解得b=1,
∴yx+1,
抛物线y=ax2﹣2ax+c的对称轴为直线x1,
在yx+1中,令x=1得y,
∴E(1,),
∵抛物线y=ax2﹣2ax+c(a>0)与x轴交于点A(﹣2,0)、B两点,
∴A(﹣2,0),B关于对称轴直线x=1对称,
∴B(4,0),
∴AB=6,
∴S△ABEAB |yE|6,
答:△ABE的面积是;
(2)过E作EK⊥y轴于K,如图:
∵,
∴,
∵OF∥EK,
∴,
由(1)知E(1,),
∴OK,
∴OC=2,
∴C(0,﹣2),
把A(﹣2,0),C(0,﹣2)代入y=ax2﹣2ax+c得:
,
解得,
∴抛物线的表达式为yx2x﹣2;
(3)过B作BP∥CE交直线AE于P,以B为圆心,BP为半径作圆与直线AE另一交点为P',如图:
由(1)(2)知直线AE为yx+1,C(0,﹣2),B(4,0),
设直线BC为y=tx﹣2,将B(4,0)代入得:
4t﹣2=0,
解得t,
∴直线BC为yx﹣2,
∴AE∥BC,
∵BP∥CE,
∴四边形ECBP是平行四边形,
∴∠ECB=∠EPB,
∴P是满足题意的点,
由C(0,﹣2)平移至B(4,0)与E(1,)平移至P方式相同,可得P(5,),
∵BP=BP',
∴∠EP'B=∠EPB=∠ECB,
∴P'是满足题意的点,
设P'(m,m+1),
∵BP=BP',
∴(5﹣4)2+(0)2=(m﹣4)2+(m+1)2,
解得m=5(与P重合,舍去)或m,
∴P'(,),
综上所述,点P的坐标为(5,)或(,).
23.【解答】(1)证明:∵∠DAE=∠BAC=α,
∴∠DAE﹣∠BAD=∠BAC﹣∠BAD,
即∠BAE=∠CAD,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(SAS),
∴∠ABE=∠ACD,
∵AB=AC,
∴∠ABC=∠ACD,
∴∠ABC=∠ABE,
∴BA平分∠EBC;
(2)解:EF=DG,
证明:如图,在AC上截取AH=AF,连接DH,在CG延长线时取点I,使CI=CH,连接DI,
在△AEF和△ADH中,
,
∴△AEF≌△ADH(SAS),
∴EF=DH,∠AFE=∠AHD,
∴∠AFD=∠CHD,
∵CG∥AB,
∴∠AFD=∠DGI,
∴∠DGI=∠CHD,
∵AB=AC,
∴∠ABC=∠ACD,
∵CG∥AB,
∴∠ABC=∠ICD,
∴∠ACD=∠ICD,
在△HCD和△ICD中,
,
∴△HCD≌△ICD(SAS),
∴∠CID=∠CHD,DI=DH,
∵∠DGI=∠CHD,
∴∠CID=∠DGI,
∴DI=DG,
∴DG=DH,
∵EF=DH,
∴EF=DG.
第1页(共1页)
