第23章《中心对称》教学课件(共26张PPT) 人教版数学九年级上册
文档属性
| 名称 | 第23章《中心对称》教学课件(共26张PPT) 人教版数学九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-30 00:00:00 | ||
图片预览



文档简介
(共26张PPT)
23.2.1 中心对称
配套人教版
学习目标
1.正确认识什么是中心对称、对称中心,理解关于中心对称的图形的性质特点.
2.能根据中心对称的性质,作出一个图形关于某点成中心对称的对称图形.
3.经历中心对称的探索过程,通过观察、操作、发现,探究中心对称的有关概念和基本性质,培养学生的观察能力和动手操作能力.
4. 通过对中心对称的学习,感受对称、匀称、均衡的美感,体验图形变化的规律,感受图形变换和图形的美丽,感受生活中的数学,培养热爱数学的情怀.
中心对称
应用新知
巩固新知
课堂小结
布置作业
A
B
C
A′
B′
C′
O
创设情境
探究新知
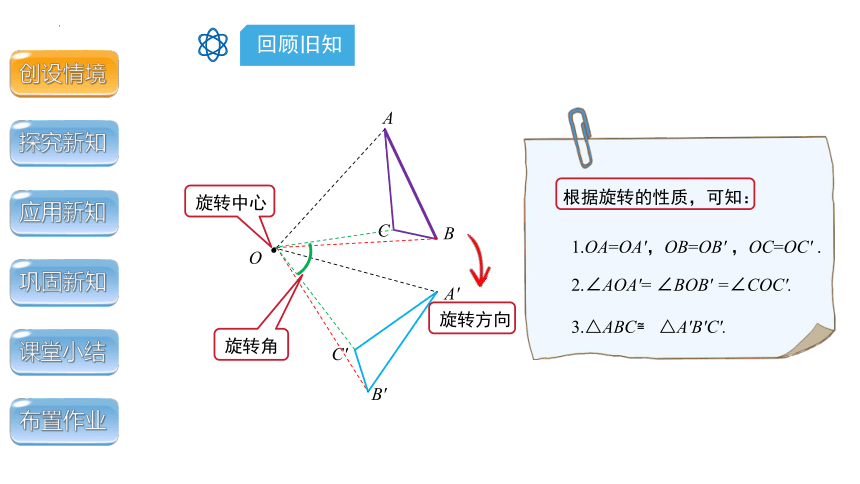
回顾旧知
旋转中心
旋转角
根据旋转的性质,可知:
1.OA=OA′,OB=OB′ ,OC=OC′ .
2.∠AOA′= ∠BOB′ =∠COC′.
3.△ABC≌ △A′B′C′.
旋转方向
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
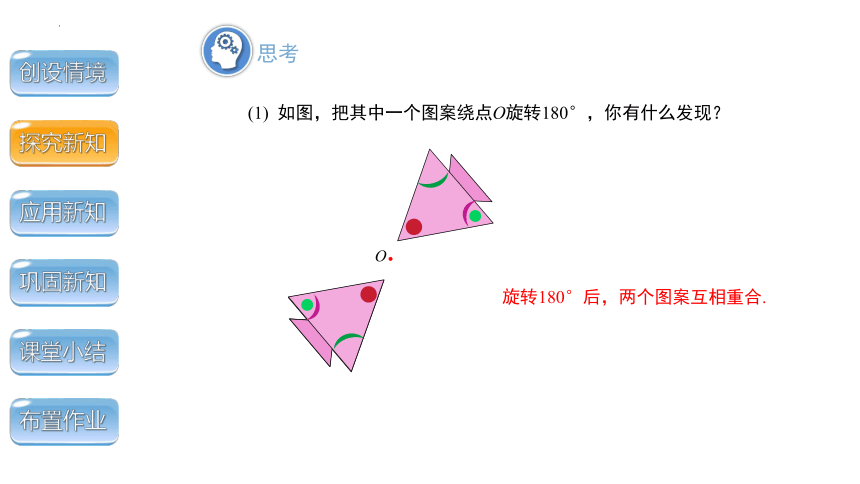
(1) 如图,把其中一个图案绕点O旋转180°,你有什么发现?
O
旋转180°后,两个图案互相重合.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
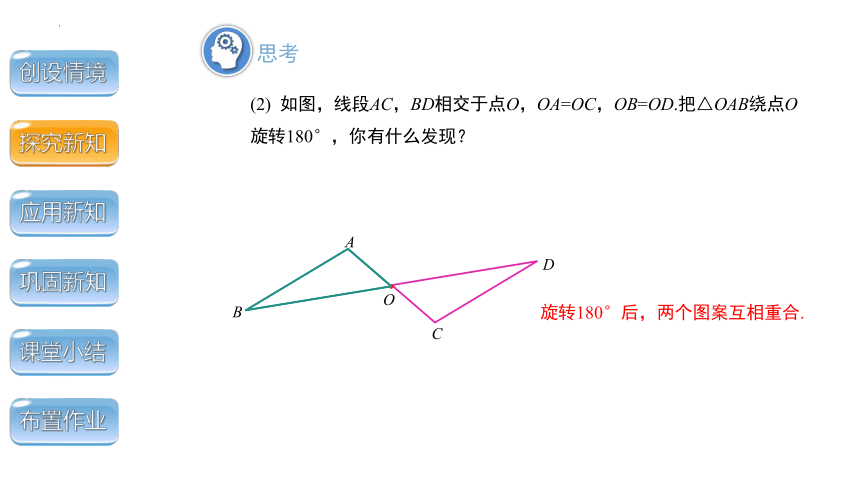
(2) 如图,线段AC,BD相交于点O,OA=OC,OB=OD.把△OAB绕点O旋转180°,你有什么发现?
O
A
B
D
C
旋转180°后,两个图案互相重合.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
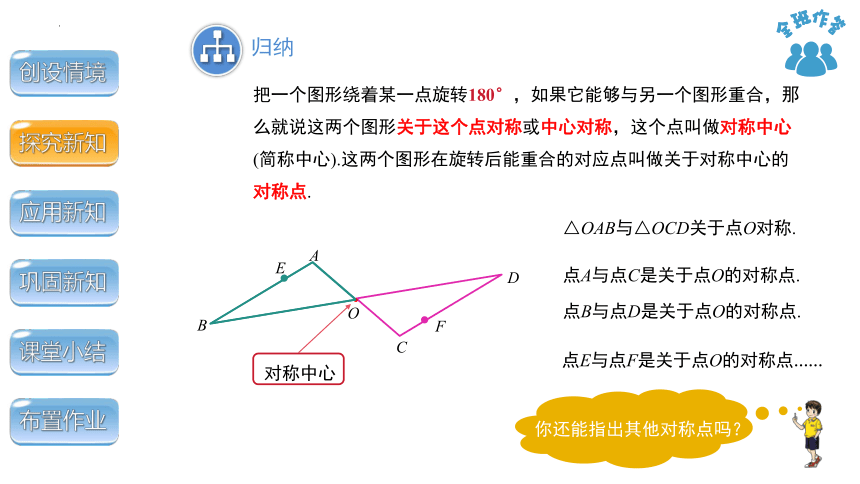
把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心(简称中心).这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点.
O
A
B
D
C
△OAB与△OCD关于点O对称.
对称中心
点A与点C是关于点O的对称点.
点B与点D是关于点O的对称点.
E
F
你还能指出其他对称点吗?
点E与点F是关于点O的对称点……
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
注意:
1. 中心对称是指两个图形间的位置关系,必须涉及两个图形.
2. 中心对称是特殊的旋转,旋转角为180°.
3. 成中心对称的两个图形,只有一个对称中心,这个对称中心可能在两个图形的外部,也可能在图形的内部或图形上,但对称点一定在对称中心的两侧或与对称中心重合.
归纳
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
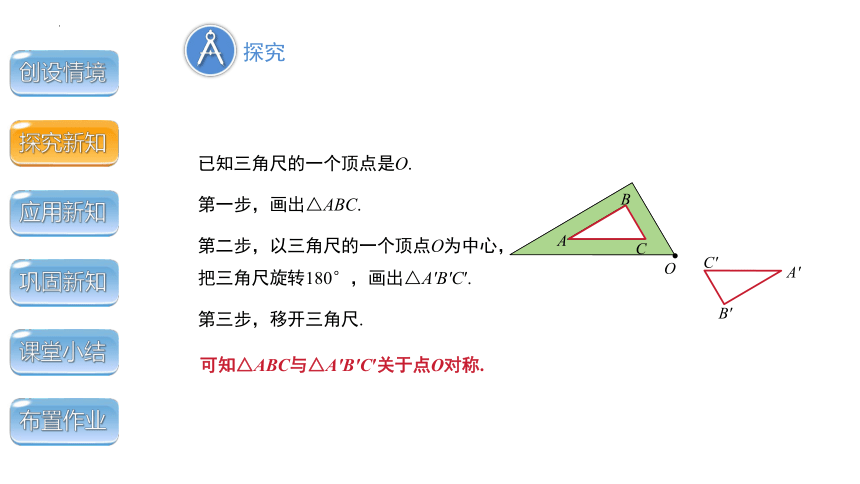
已知三角尺的一个顶点是O.
探究
A
B
C
A′
B′
C′
第一步,画出△ABC.
第二步,以三角尺的一个顶点O为中心,把三角尺旋转180°,画出△A′B′C′.
第三步,移开三角尺.
O
可知△ABC与△A′B′C′关于点O对称.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
A
B
C
A′
B′
C′
O
思考
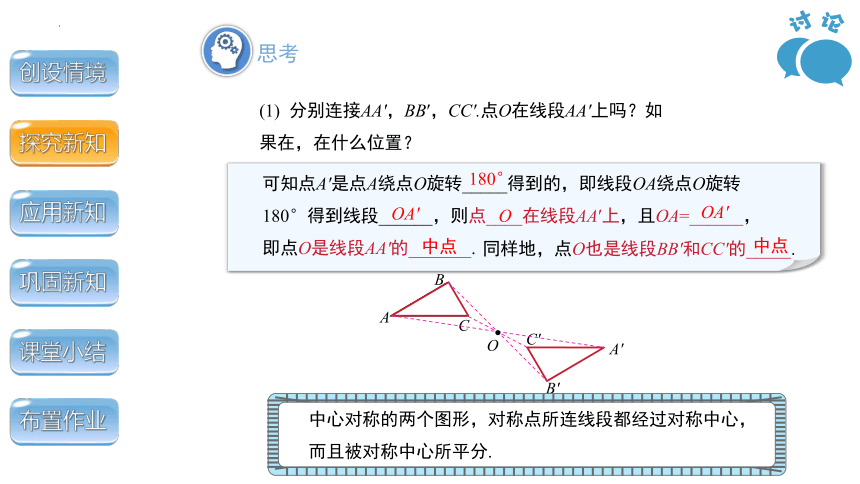
(1) 分别连接AA′,BB′,CC′.点O在线段AA′上吗?如果在,在什么位置?
可知点A′是点A绕点O旋转_____得到的,即线段OA绕点O旋转180°得到线段______,则点____在线段AA′上,且OA=______,即点O是线段AA′的_______.
180°
OA′
O
OA′
中点
同样地,点O也是线段BB′和CC′的_____.
中点
中心对称的两个图形,对称点所连线段都经过对称中心,
而且被对称中心所平分.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
A
B
C
A′
B′
C′
O
△ABC≌△A′B′C′.
思考
(2) △ABC与△A′B′C′有什么关系?
中心对称的两个图形是全等的.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
中心对称的性质:
1. 中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分.
2. 中心对称的两个图形是全等的.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
做一做
如图,△ABC与△A′B′C′关于点O中心对称,则:
A
B
C
A′
B′
C′
(1) △ABC_______△A′B′C′.
(2) OA=____,OB=____, OC=____.
(3) AA′,BB′, CC′都经过点_____.
(4) 点O是线段_____、_____、______的中点.
≌
OA′
OB′
OC′
O
AA′
BB′
CC′
O
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
旋转和中心对称的联系和区别.
联系
区别
中心对称
一般旋转
都是绕着_____________
旋转角度都是______
旋转角度________
归纳
某一点进行旋转
180°
不固定
中心对称是一种特殊的旋转.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
轴对称
中心对称
有一条对称轴——直线
图形绕中心旋转(旋转180°)
有一个对称中心——点
图形沿轴对折(翻转180°)
对称点连线的垂直平分线是对称轴
对称点连线的中点是对称中心
翻转后与另一个图形重合
旋转后与另一个图形重合
A
B
C
A′
B′
C′
A
B
C
A′
B′
C′
中心对称与轴对称的对比
归纳
巩固新知
课堂小结
布置作业
探究新知
典型例题
创设情境
应用新知
(1) 如图,选择点O为对称中心,画出点A关于点O的对称点A′.
O
A
A′
第一步:连接AO.
第二步:延长AO至A′,使OA=OA′,即可以求得点A关于点O的对称点为A′.
巩固新知
课堂小结
布置作业
探究新知
典型例题
创设情境
应用新知
(2) 如图,线段AB和点O,画出线段AB关于点O的对称线段A′B′ .
O
A
A′
第一步:连接AO并延长到A′,使OA′=OA,则得A的对称点A′.
第三步:连接A′B′,即可以求得线段AB关于点O的对称线段A′B′.
B
第二步:连接BO并延长到B′,使OB′=OB,则得B的对称点B′.
B′
巩固新知
课堂小结
布置作业
探究新知
典型例题
创设情境
应用新知
(3) 如图,选择点O为对称中心,画出与△ABC关于点O对称的△A′B′C′.
O
A
B
C
A′
B′
C′
作出A,B,C三点关于点O的对称点A′,B′,C′,依次连接A′B′ , B′C′ , C′A′ ,就可得到与△ABC关于点O对称的△A′B′C′.
巩固新知
课堂小结
布置作业
创设情境
归纳
画出一个图形关于某点对称的图形的一般步骤:
探究新知
应用新知
1. 确定关键点(通常为图形顶点等特殊点).
2. 做关键点关于旋转中心的对称点.
3. 顺次连接对应点,组成的图形为所求.
应用新知
课堂小结
布置作业
创设情境
练习1
随堂练习
探究新知
巩固新知
以下说法中,关于中心对称的描述不正确的是( )
A.把一个图形绕着某一点旋转,如果它能与另一个图形重合,那么就说这两个图形中心对称.
B.关于中心对称的两个图形是全等的.
C.关于中心对称的两个图形,对称点的连线必过对称中心.
D.如果两个图形关于点O对称,点A与点A'是对称点,那么OA=OA'.
A
应用新知
课堂小结
布置作业
创设情境
练习2
随堂练习
探究新知
巩固新知
如图已知△ABC与△A′B′C′关于点O成中心对称,则下列判断不正确的是( ).
A. ∠ABC=∠A′B′C′
B. ∠BOC=∠B′A′C′
C. AB=A′B′
D. OA=OA′
O
A
B
A′
B′
C′
C
B
应用新知
课堂小结
布置作业
创设情境
练习3
随堂练习
探究新知
巩固新知
如图,已知△ABC与△A′B′C′关于某点成中心对称,求出它们的对称中心O.
O
A
B
A′
B′
C′
C
方法1:连接一组对应点(例BB′),用刻度尺找出BB′的中点O,则点O即为所求.
方法2:连接两组对应点(例CC′ ,BB′),两个线段的交点为O,则点O即为所求.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
中心对称
中心对称的性质:
1. 中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分.
2. 中心对称的两个图形是全等的.
注意:
1. 中心对称是指两个图形间的位置关系,必须涉及两个图形.
2. 中心对称是特殊的旋转,旋转角为180°.
3. 成中心对称的两个图形,只有一个对称中心,这个对称中心可能在两个图形的外部,也可能在图形的内部或图形上,但对称点一定在对称中心的两侧或与对称中心重合.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
中心对称
画出一个图形关于某点对称的图形的一般步骤:
1. 确定关键点(通常为图形顶点等特殊点).
2. 做关键点关于旋转中心的对称点.
3. 顺次连接对应点,组成的图形为所求.
旋转和中心对称的联系和区别.
联系
区别
中心对称
一般旋转
都是绕着_____________
旋转角度都是______
旋转角度________
某一点进行旋转
180°
不固定
中心对称是一种特殊的旋转.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
中心对称
轴对称
中心对称
有一条对称轴——直线
图形绕中心旋转(旋转180°)
有一个对称中心——点
图形沿轴对折(翻转180°)
对称点连线的垂直平分线是对称轴
对称点连线的中点是对称中心
翻转后与另一个图形重合
旋转后与另一个图形重合
A
B
C
A′
B′
C′
A
B
C
A′
B′
C′
中心对称与轴对称的对比
布置作业
教科书第66页,练习1、2.
教科书第69页,习题1.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
23.2.1 中心对称
配套人教版
学习目标
1.正确认识什么是中心对称、对称中心,理解关于中心对称的图形的性质特点.
2.能根据中心对称的性质,作出一个图形关于某点成中心对称的对称图形.
3.经历中心对称的探索过程,通过观察、操作、发现,探究中心对称的有关概念和基本性质,培养学生的观察能力和动手操作能力.
4. 通过对中心对称的学习,感受对称、匀称、均衡的美感,体验图形变化的规律,感受图形变换和图形的美丽,感受生活中的数学,培养热爱数学的情怀.
中心对称
应用新知
巩固新知
课堂小结
布置作业
A
B
C
A′
B′
C′
O
创设情境
探究新知
回顾旧知
旋转中心
旋转角
根据旋转的性质,可知:
1.OA=OA′,OB=OB′ ,OC=OC′ .
2.∠AOA′= ∠BOB′ =∠COC′.
3.△ABC≌ △A′B′C′.
旋转方向
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
(1) 如图,把其中一个图案绕点O旋转180°,你有什么发现?
O
旋转180°后,两个图案互相重合.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
(2) 如图,线段AC,BD相交于点O,OA=OC,OB=OD.把△OAB绕点O旋转180°,你有什么发现?
O
A
B
D
C
旋转180°后,两个图案互相重合.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心(简称中心).这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点.
O
A
B
D
C
△OAB与△OCD关于点O对称.
对称中心
点A与点C是关于点O的对称点.
点B与点D是关于点O的对称点.
E
F
你还能指出其他对称点吗?
点E与点F是关于点O的对称点……
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
注意:
1. 中心对称是指两个图形间的位置关系,必须涉及两个图形.
2. 中心对称是特殊的旋转,旋转角为180°.
3. 成中心对称的两个图形,只有一个对称中心,这个对称中心可能在两个图形的外部,也可能在图形的内部或图形上,但对称点一定在对称中心的两侧或与对称中心重合.
归纳
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
已知三角尺的一个顶点是O.
探究
A
B
C
A′
B′
C′
第一步,画出△ABC.
第二步,以三角尺的一个顶点O为中心,把三角尺旋转180°,画出△A′B′C′.
第三步,移开三角尺.
O
可知△ABC与△A′B′C′关于点O对称.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
A
B
C
A′
B′
C′
O
思考
(1) 分别连接AA′,BB′,CC′.点O在线段AA′上吗?如果在,在什么位置?
可知点A′是点A绕点O旋转_____得到的,即线段OA绕点O旋转180°得到线段______,则点____在线段AA′上,且OA=______,即点O是线段AA′的_______.
180°
OA′
O
OA′
中点
同样地,点O也是线段BB′和CC′的_____.
中点
中心对称的两个图形,对称点所连线段都经过对称中心,
而且被对称中心所平分.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
A
B
C
A′
B′
C′
O
△ABC≌△A′B′C′.
思考
(2) △ABC与△A′B′C′有什么关系?
中心对称的两个图形是全等的.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
中心对称的性质:
1. 中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分.
2. 中心对称的两个图形是全等的.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
做一做
如图,△ABC与△A′B′C′关于点O中心对称,则:
A
B
C
A′
B′
C′
(1) △ABC_______△A′B′C′.
(2) OA=____,OB=____, OC=____.
(3) AA′,BB′, CC′都经过点_____.
(4) 点O是线段_____、_____、______的中点.
≌
OA′
OB′
OC′
O
AA′
BB′
CC′
O
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
旋转和中心对称的联系和区别.
联系
区别
中心对称
一般旋转
都是绕着_____________
旋转角度都是______
旋转角度________
归纳
某一点进行旋转
180°
不固定
中心对称是一种特殊的旋转.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
轴对称
中心对称
有一条对称轴——直线
图形绕中心旋转(旋转180°)
有一个对称中心——点
图形沿轴对折(翻转180°)
对称点连线的垂直平分线是对称轴
对称点连线的中点是对称中心
翻转后与另一个图形重合
旋转后与另一个图形重合
A
B
C
A′
B′
C′
A
B
C
A′
B′
C′
中心对称与轴对称的对比
归纳
巩固新知
课堂小结
布置作业
探究新知
典型例题
创设情境
应用新知
(1) 如图,选择点O为对称中心,画出点A关于点O的对称点A′.
O
A
A′
第一步:连接AO.
第二步:延长AO至A′,使OA=OA′,即可以求得点A关于点O的对称点为A′.
巩固新知
课堂小结
布置作业
探究新知
典型例题
创设情境
应用新知
(2) 如图,线段AB和点O,画出线段AB关于点O的对称线段A′B′ .
O
A
A′
第一步:连接AO并延长到A′,使OA′=OA,则得A的对称点A′.
第三步:连接A′B′,即可以求得线段AB关于点O的对称线段A′B′.
B
第二步:连接BO并延长到B′,使OB′=OB,则得B的对称点B′.
B′
巩固新知
课堂小结
布置作业
探究新知
典型例题
创设情境
应用新知
(3) 如图,选择点O为对称中心,画出与△ABC关于点O对称的△A′B′C′.
O
A
B
C
A′
B′
C′
作出A,B,C三点关于点O的对称点A′,B′,C′,依次连接A′B′ , B′C′ , C′A′ ,就可得到与△ABC关于点O对称的△A′B′C′.
巩固新知
课堂小结
布置作业
创设情境
归纳
画出一个图形关于某点对称的图形的一般步骤:
探究新知
应用新知
1. 确定关键点(通常为图形顶点等特殊点).
2. 做关键点关于旋转中心的对称点.
3. 顺次连接对应点,组成的图形为所求.
应用新知
课堂小结
布置作业
创设情境
练习1
随堂练习
探究新知
巩固新知
以下说法中,关于中心对称的描述不正确的是( )
A.把一个图形绕着某一点旋转,如果它能与另一个图形重合,那么就说这两个图形中心对称.
B.关于中心对称的两个图形是全等的.
C.关于中心对称的两个图形,对称点的连线必过对称中心.
D.如果两个图形关于点O对称,点A与点A'是对称点,那么OA=OA'.
A
应用新知
课堂小结
布置作业
创设情境
练习2
随堂练习
探究新知
巩固新知
如图已知△ABC与△A′B′C′关于点O成中心对称,则下列判断不正确的是( ).
A. ∠ABC=∠A′B′C′
B. ∠BOC=∠B′A′C′
C. AB=A′B′
D. OA=OA′
O
A
B
A′
B′
C′
C
B
应用新知
课堂小结
布置作业
创设情境
练习3
随堂练习
探究新知
巩固新知
如图,已知△ABC与△A′B′C′关于某点成中心对称,求出它们的对称中心O.
O
A
B
A′
B′
C′
C
方法1:连接一组对应点(例BB′),用刻度尺找出BB′的中点O,则点O即为所求.
方法2:连接两组对应点(例CC′ ,BB′),两个线段的交点为O,则点O即为所求.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
中心对称
中心对称的性质:
1. 中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分.
2. 中心对称的两个图形是全等的.
注意:
1. 中心对称是指两个图形间的位置关系,必须涉及两个图形.
2. 中心对称是特殊的旋转,旋转角为180°.
3. 成中心对称的两个图形,只有一个对称中心,这个对称中心可能在两个图形的外部,也可能在图形的内部或图形上,但对称点一定在对称中心的两侧或与对称中心重合.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
中心对称
画出一个图形关于某点对称的图形的一般步骤:
1. 确定关键点(通常为图形顶点等特殊点).
2. 做关键点关于旋转中心的对称点.
3. 顺次连接对应点,组成的图形为所求.
旋转和中心对称的联系和区别.
联系
区别
中心对称
一般旋转
都是绕着_____________
旋转角度都是______
旋转角度________
某一点进行旋转
180°
不固定
中心对称是一种特殊的旋转.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
中心对称
轴对称
中心对称
有一条对称轴——直线
图形绕中心旋转(旋转180°)
有一个对称中心——点
图形沿轴对折(翻转180°)
对称点连线的垂直平分线是对称轴
对称点连线的中点是对称中心
翻转后与另一个图形重合
旋转后与另一个图形重合
A
B
C
A′
B′
C′
A
B
C
A′
B′
C′
中心对称与轴对称的对比
布置作业
教科书第66页,练习1、2.
教科书第69页,习题1.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
同课章节目录
