【核心素养目标】苏科版七年级上册数学5.4 第2课时 根据三视图还原几何体 课件 (共22张PPT)
文档属性
| 名称 | 【核心素养目标】苏科版七年级上册数学5.4 第2课时 根据三视图还原几何体 课件 (共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 875.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-29 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
第5章 走进图形世界
5.4 主视图、左视图、俯视图
第2课时 根据三视图还原几何体
1.能用三视图确定立体图形;
2.能将三视图、立体图形与展开平面图形相互转化.
◎重点:根据三视图确定立体图形.
◎难点:感知立体图形与平面图形的关系.
上节课我们学习了由立体图形得到三视图,反过来由三视图可还原立体图形,下面我们一起进行探索.
由三视图判断几何体
阅读课本本课时第136页“想一想”到第137页例题的内容,完成下列问题.
由三视图想象几何体的形状,应分别根据主视图、俯视图和左视图想象几何体的 前面 、 上面 和 左面 的形状,然后综合起来考虑整体形状.
前面
上面
左面
1.某几何体的三视图如图所示,则此几何体是( C )
A.圆锥
B.长方体
C.圆柱
D.四棱柱
C
2.如图,这是某几何体的三视图,该几何体是( D )
A.正方体
B.圆锥
C.圆柱
D.球
D
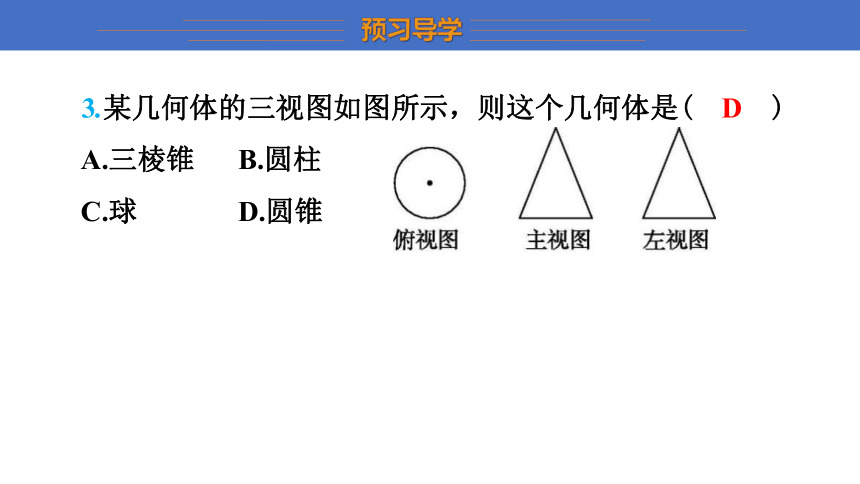
3.某几何体的三视图如图所示,则这个几何体是( D )
A.三棱锥 B.圆柱
C.球 D.圆锥
D
4.如图,根据三视图,这个立体图形的名称是( A )
A.三棱柱
B.圆柱
C.三棱锥
D.圆锥
A
1.一个几何体的三个视图如图所示(单位:cm).
(1)该几何体的名称是 .
(2)若其俯视图为正方形,根据图中数据计算这个几何体的表面积.
解:(1)根据三视图可得这个几何体是长方体.
(2)由三视图知,几何体是一个长方体,
长方体的底面是边长为3的正方形,高是4,
则这个几何体的表面积是2×(3×3+3×4
+3×4)=66(cm2).
答:这个几何体的表面积是66 cm2.
2.一个几何体的三种视图如图所示.
(1)这个几何体的名称是 .
(2)求这个几何体的表面积.
(3)求这个几何体的体积.
解:(1)这个几何体的名称是圆柱体.
(2)这个圆柱的表面积=2×π×+4×π×6=32π.
(3)圆柱的体积=π××6=24π.
3.一个物体由几个相同的正方体堆叠而成,从三个不同方向观察得到的图形如图所示,试回答下面的问题:
(1)该物体共有几层?
(2)该物体一共需要几个正方体叠成?
解:(1)由正方体堆叠而成的立体图形有3层高.
(2)5+3+1=9(个).故一共需要9个
正方体叠成.
变式训练 下面是由一些棱长为a厘米的正方体小木块搭建成的几何体的主视图、左视图和俯视图.
(1)该几何体是由 块小木块组成的.
(2)求出该几何体的体积.
(3)求出该几何体的表面积(包含底面).
解:(1)几何体的小正方形的个数如俯视图所示,2+1+3+1+1+2=10.
(2)V=10a3(cm3),所以该几何体的体积为10a3 cm3.
(3)S=2(6a2+6a2+6a2)+2(a2+a2)=40a2(cm2),所以该几何体的表面积为40a2 cm2.
1.如图,这是从上面看一个几何体得到的图形,则该几何体可能是( D )
D
2.如图,三视图所对应的直观图是下面的( C )
C
3.如图,这是一个几何体的主视图,则这个几何体可能是
( A )
A
4.下图是某几何体从三个方向看到的形状,则这个几何体最多由 11 个小正方体组成.
11
5.下图(单位:cm)是某校升旗台的三视图.
(1)用萝卜做出台阶的立体模型.
(2)计算出台阶的体积.
解:(1)立体模型如下图.
(2)台阶的体积可以用三个长方体的体积来求得,即V=V1+V2+V3=150×(800+1600+2400)=150×4800=720000(cm3).
第5章 走进图形世界
5.4 主视图、左视图、俯视图
第2课时 根据三视图还原几何体
1.能用三视图确定立体图形;
2.能将三视图、立体图形与展开平面图形相互转化.
◎重点:根据三视图确定立体图形.
◎难点:感知立体图形与平面图形的关系.
上节课我们学习了由立体图形得到三视图,反过来由三视图可还原立体图形,下面我们一起进行探索.
由三视图判断几何体
阅读课本本课时第136页“想一想”到第137页例题的内容,完成下列问题.
由三视图想象几何体的形状,应分别根据主视图、俯视图和左视图想象几何体的 前面 、 上面 和 左面 的形状,然后综合起来考虑整体形状.
前面
上面
左面
1.某几何体的三视图如图所示,则此几何体是( C )
A.圆锥
B.长方体
C.圆柱
D.四棱柱
C
2.如图,这是某几何体的三视图,该几何体是( D )
A.正方体
B.圆锥
C.圆柱
D.球
D
3.某几何体的三视图如图所示,则这个几何体是( D )
A.三棱锥 B.圆柱
C.球 D.圆锥
D
4.如图,根据三视图,这个立体图形的名称是( A )
A.三棱柱
B.圆柱
C.三棱锥
D.圆锥
A
1.一个几何体的三个视图如图所示(单位:cm).
(1)该几何体的名称是 .
(2)若其俯视图为正方形,根据图中数据计算这个几何体的表面积.
解:(1)根据三视图可得这个几何体是长方体.
(2)由三视图知,几何体是一个长方体,
长方体的底面是边长为3的正方形,高是4,
则这个几何体的表面积是2×(3×3+3×4
+3×4)=66(cm2).
答:这个几何体的表面积是66 cm2.
2.一个几何体的三种视图如图所示.
(1)这个几何体的名称是 .
(2)求这个几何体的表面积.
(3)求这个几何体的体积.
解:(1)这个几何体的名称是圆柱体.
(2)这个圆柱的表面积=2×π×+4×π×6=32π.
(3)圆柱的体积=π××6=24π.
3.一个物体由几个相同的正方体堆叠而成,从三个不同方向观察得到的图形如图所示,试回答下面的问题:
(1)该物体共有几层?
(2)该物体一共需要几个正方体叠成?
解:(1)由正方体堆叠而成的立体图形有3层高.
(2)5+3+1=9(个).故一共需要9个
正方体叠成.
变式训练 下面是由一些棱长为a厘米的正方体小木块搭建成的几何体的主视图、左视图和俯视图.
(1)该几何体是由 块小木块组成的.
(2)求出该几何体的体积.
(3)求出该几何体的表面积(包含底面).
解:(1)几何体的小正方形的个数如俯视图所示,2+1+3+1+1+2=10.
(2)V=10a3(cm3),所以该几何体的体积为10a3 cm3.
(3)S=2(6a2+6a2+6a2)+2(a2+a2)=40a2(cm2),所以该几何体的表面积为40a2 cm2.
1.如图,这是从上面看一个几何体得到的图形,则该几何体可能是( D )
D
2.如图,三视图所对应的直观图是下面的( C )
C
3.如图,这是一个几何体的主视图,则这个几何体可能是
( A )
A
4.下图是某几何体从三个方向看到的形状,则这个几何体最多由 11 个小正方体组成.
11
5.下图(单位:cm)是某校升旗台的三视图.
(1)用萝卜做出台阶的立体模型.
(2)计算出台阶的体积.
解:(1)立体模型如下图.
(2)台阶的体积可以用三个长方体的体积来求得,即V=V1+V2+V3=150×(800+1600+2400)=150×4800=720000(cm3).
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
