【核心素养目标】苏科版七年级数学上册5.3 展开与折叠 课件 (共23张PPT)
文档属性
| 名称 | 【核心素养目标】苏科版七年级数学上册5.3 展开与折叠 课件 (共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 847.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-29 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
第5章 走进图形世界
5.3 展开与折叠
1.认识直棱柱、圆锥等简单立体图形的侧面展开图;
2.能根据展开图初步判断和折叠立体模型,进一步认识立体图形与平面图形的关系;
3.通过观察、操作、推断等数学活动,积累数学活动经验,发展空间想象能力.
◎重点:直棱柱、圆锥的展开图.
◎难点:正方体的展开与折叠.
图1是一个包装盒,图2是包装盒的用料,你知道它们之间的关系吗?下面我们一起来寻找其中的规律.
几何体的展开图
阅读课本本课时第129页全部内容,完成下列问题.
1.立体图形是由 平面 图形围成的.沿着 棱 剪开就得到平面图形,这样的平面图形就是相应立体图形的展开图.同一个立体图形按不同的方式展开,得到的平面展开图是 不一样 的.
平面
棱
不一样
2.常见几何体的侧面展开图:
①圆柱的侧面展开图是 长方形 .②圆锥的侧面展开图是 扇形 .③长方体的侧面展开图是 长方形 .④三棱柱的侧面展开图是 长方形 .
长方形
扇形
长方形
长方形
展开图折叠成几何体
阅读课本本课时第130页“练一练”后到第131页“练一练”前的内容,完成下列问题.
通过结合 立体图形 与 平面图形 的相互转化,去理解和掌握几何体的 展开图 ,要注意多从实物出发,然后再从给定的图形中辨认它们能否折叠成给定的立体图形.
立体图形
平面图形
展开图
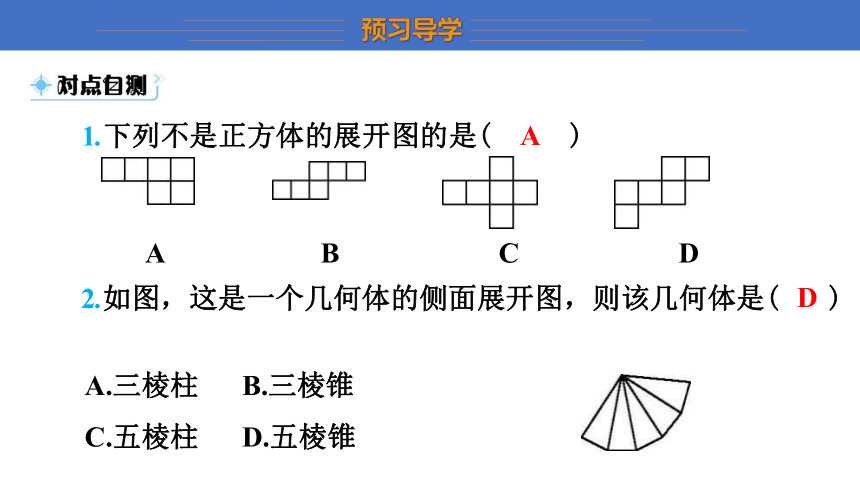
1.下列不是正方体的展开图的是( A )
A B C D
2.如图,这是一个几何体的侧面展开图,则该几何体是( D)
A.三棱柱 B.三棱锥
C.五棱柱 D.五棱锥
A
D
3. 把图中的纸片沿虚线折叠,可以围成( C )
A.三棱锥 B.三棱柱
C.五棱锥 D.五棱柱
4.下列图形能折叠成圆锥的是( B )
A B C D
C
B
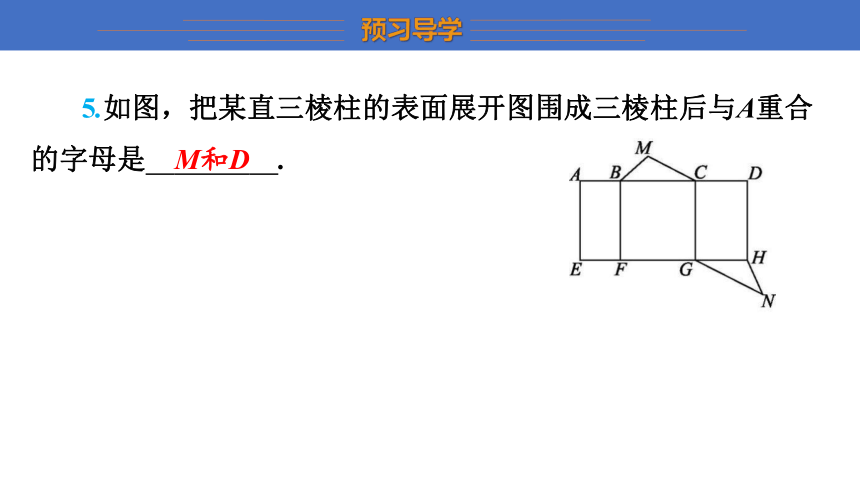
5.如图,把某直三棱柱的表面展开图围成三棱柱后与A重合的字母是 M和D .
M和D
1.如图,第一行的图形分别是第二行中的几何体展开的形状,请你把有对应关系的平面图形与立体图形用线连一连.
解:由简单几何体的展开与折叠可得.
变式训练 如图,这些平面图形分别是由哪种几何体展开形成的?
(1) 正方体 ;(2) 长方体 ;(3) 三棱柱 ;
(4) 四棱锥 ;(5) 圆柱 ;(6) 三棱柱 .
正方体
长方体
三棱柱
四棱锥
圆柱
三棱柱
2.马小虎准备制作一个封闭的正方体盒子,他先用4个大小一样的正方形制成如下图所示拼接图形(实线部分),经折叠后发现还少一个面,请你在下图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(添加所有符合要求的正方形,添加的正方形用阴影表示)
解:如图所示:
3. 如图,这是一个正方体的表面展开图,请回答下列问题:
(1)与面C相对的面是 ,与面A相对的面是 ;
(2)若A=a3-2ab2,B=ab2+3,C=a3-1,D=ab2-3,且相对的两个面所表示的代数式的和都相等,求E,F分别表示的代数式.
解:(1)由正方体表面展开图的“相间、Z端是对面”可知,
“C”与“E”是对面,“A”与“D”是对面.
(2)由题意得,A+D=C+E=B+F,
所以E=A+D-C=(a3-2ab2)+(ab2-3)-(a3-1)=a3-2ab2+ab2-3-a3+1=-ab2-2,
所以F=A+D-B=(a3-2ab2)+(ab2-3)-(ab2+3)=a3-2ab2+ab2-3-ab2-3=a3-2ab2-6.
变式训练 李明同学设计了某个产品的正方体包装盒如图所示,由于粗心少设计了其中一个顶盖,请你把它补上,使其成为一个两面均有盖的正方体盒子.
(1)共有 种弥补方法;
(2)任意画出一种成功的设计图(在图中补充);
(3)在你帮忙设计成功的图中,要把-6,8,10,-10,-8,6这些数字分别填入六个小正方形,使得折成的正方体相对面上的两个数相加等于0.(直接在图中填上)
解:(1)4.
(2)如图所示(画法不唯一):
(3)如图所示:
1.如图,这是某几何体的表面展开图,该几何体是( C )
A.长方体 B.圆柱
C.圆锥 D.直三棱柱
C
2.把如图所示的纸片沿着虚线折叠,可以得到的几何体是
( A )
A.三棱柱 B.四棱柱
C.三棱锥 D.四棱锥
A
3.一个正方体的表面分别标有百、年、峥、嵘、岁、月,下面是该正方体的一个展开图,已知“嵘”的对面为“岁”,则
( B )
A.▲代表“岁” B.▲代表“月”
C.★代表“月” D.◆代表“月”
B
4.已知图1的小正方形和图2中所有的小正方形边长都相等,将图1的小正方形安放在图2中的①、②、③、④的其中某一个位置,放置后所组成的图形能围成一个正方体,则安放的位置不能是 ① .
①
第5章 走进图形世界
5.3 展开与折叠
1.认识直棱柱、圆锥等简单立体图形的侧面展开图;
2.能根据展开图初步判断和折叠立体模型,进一步认识立体图形与平面图形的关系;
3.通过观察、操作、推断等数学活动,积累数学活动经验,发展空间想象能力.
◎重点:直棱柱、圆锥的展开图.
◎难点:正方体的展开与折叠.
图1是一个包装盒,图2是包装盒的用料,你知道它们之间的关系吗?下面我们一起来寻找其中的规律.
几何体的展开图
阅读课本本课时第129页全部内容,完成下列问题.
1.立体图形是由 平面 图形围成的.沿着 棱 剪开就得到平面图形,这样的平面图形就是相应立体图形的展开图.同一个立体图形按不同的方式展开,得到的平面展开图是 不一样 的.
平面
棱
不一样
2.常见几何体的侧面展开图:
①圆柱的侧面展开图是 长方形 .②圆锥的侧面展开图是 扇形 .③长方体的侧面展开图是 长方形 .④三棱柱的侧面展开图是 长方形 .
长方形
扇形
长方形
长方形
展开图折叠成几何体
阅读课本本课时第130页“练一练”后到第131页“练一练”前的内容,完成下列问题.
通过结合 立体图形 与 平面图形 的相互转化,去理解和掌握几何体的 展开图 ,要注意多从实物出发,然后再从给定的图形中辨认它们能否折叠成给定的立体图形.
立体图形
平面图形
展开图
1.下列不是正方体的展开图的是( A )
A B C D
2.如图,这是一个几何体的侧面展开图,则该几何体是( D)
A.三棱柱 B.三棱锥
C.五棱柱 D.五棱锥
A
D
3. 把图中的纸片沿虚线折叠,可以围成( C )
A.三棱锥 B.三棱柱
C.五棱锥 D.五棱柱
4.下列图形能折叠成圆锥的是( B )
A B C D
C
B
5.如图,把某直三棱柱的表面展开图围成三棱柱后与A重合的字母是 M和D .
M和D
1.如图,第一行的图形分别是第二行中的几何体展开的形状,请你把有对应关系的平面图形与立体图形用线连一连.
解:由简单几何体的展开与折叠可得.
变式训练 如图,这些平面图形分别是由哪种几何体展开形成的?
(1) 正方体 ;(2) 长方体 ;(3) 三棱柱 ;
(4) 四棱锥 ;(5) 圆柱 ;(6) 三棱柱 .
正方体
长方体
三棱柱
四棱锥
圆柱
三棱柱
2.马小虎准备制作一个封闭的正方体盒子,他先用4个大小一样的正方形制成如下图所示拼接图形(实线部分),经折叠后发现还少一个面,请你在下图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(添加所有符合要求的正方形,添加的正方形用阴影表示)
解:如图所示:
3. 如图,这是一个正方体的表面展开图,请回答下列问题:
(1)与面C相对的面是 ,与面A相对的面是 ;
(2)若A=a3-2ab2,B=ab2+3,C=a3-1,D=ab2-3,且相对的两个面所表示的代数式的和都相等,求E,F分别表示的代数式.
解:(1)由正方体表面展开图的“相间、Z端是对面”可知,
“C”与“E”是对面,“A”与“D”是对面.
(2)由题意得,A+D=C+E=B+F,
所以E=A+D-C=(a3-2ab2)+(ab2-3)-(a3-1)=a3-2ab2+ab2-3-a3+1=-ab2-2,
所以F=A+D-B=(a3-2ab2)+(ab2-3)-(ab2+3)=a3-2ab2+ab2-3-ab2-3=a3-2ab2-6.
变式训练 李明同学设计了某个产品的正方体包装盒如图所示,由于粗心少设计了其中一个顶盖,请你把它补上,使其成为一个两面均有盖的正方体盒子.
(1)共有 种弥补方法;
(2)任意画出一种成功的设计图(在图中补充);
(3)在你帮忙设计成功的图中,要把-6,8,10,-10,-8,6这些数字分别填入六个小正方形,使得折成的正方体相对面上的两个数相加等于0.(直接在图中填上)
解:(1)4.
(2)如图所示(画法不唯一):
(3)如图所示:
1.如图,这是某几何体的表面展开图,该几何体是( C )
A.长方体 B.圆柱
C.圆锥 D.直三棱柱
C
2.把如图所示的纸片沿着虚线折叠,可以得到的几何体是
( A )
A.三棱柱 B.四棱柱
C.三棱锥 D.四棱锥
A
3.一个正方体的表面分别标有百、年、峥、嵘、岁、月,下面是该正方体的一个展开图,已知“嵘”的对面为“岁”,则
( B )
A.▲代表“岁” B.▲代表“月”
C.★代表“月” D.◆代表“月”
B
4.已知图1的小正方形和图2中所有的小正方形边长都相等,将图1的小正方形安放在图2中的①、②、③、④的其中某一个位置,放置后所组成的图形能围成一个正方体,则安放的位置不能是 ① .
①
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
