27.2.1相似三角形的判定—基本事实及其应用 教学课件(共23张PPT) 人教版数学九年级下册
文档属性
| 名称 | 27.2.1相似三角形的判定—基本事实及其应用 教学课件(共23张PPT) 人教版数学九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1017.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-30 12:29:22 | ||
图片预览



文档简介
(共23张PPT)
27.2.1 相似三角形的判定
——基本事实及其应用
学习目标
掌握相似三角形的定义和性质,明确定义是第一种判定方法;
掌握基本事实,并能够迁移到三角形中,得到对应结论;
利用基本事实证明平行于三角形一边的直线截取的两个三角形相似;
4. 探究经历“试验、猜想、证明”的过程,感受几何命题的合理性,并通过证明确认命题正确,培养学生发现问题、解决问题的能力.
重点
基本事实
难点
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
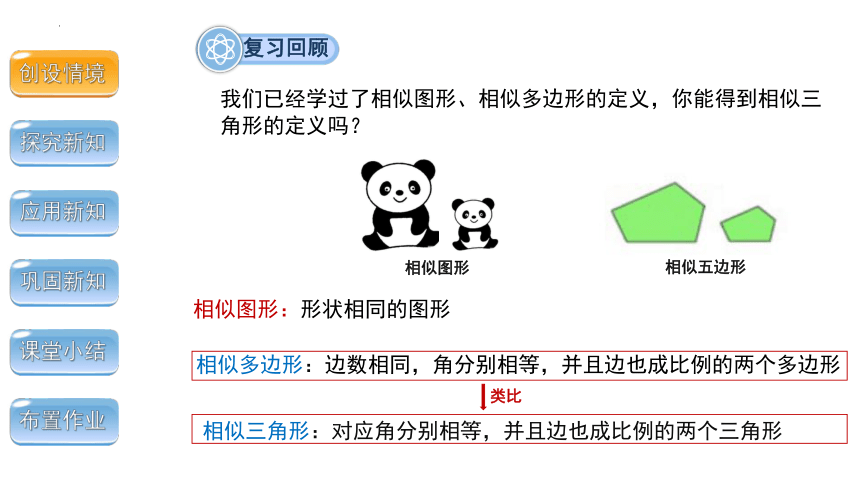
我们已经学过了相似图形、相似多边形的定义,你能得到相似三角形的定义吗?
复习回顾
相似图形:形状相同的图形
相似图形
相似五边形
相似多边形:边数相同,角分别相等,并且边也成比例的两个多边形
相似三角形:对应角分别相等,并且边也成比例的两个三角形
类比
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
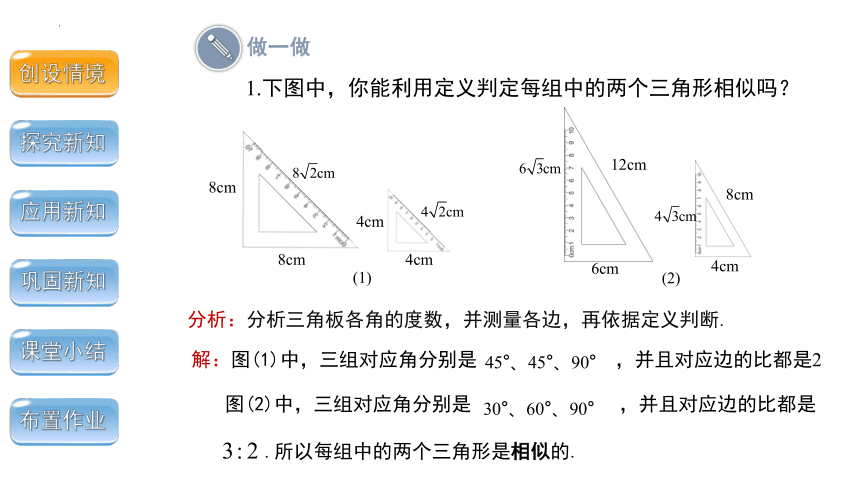
1.下图中,你能利用定义判定每组中的两个三角形相似吗?
(1)
(2)
8cm
4cm
8cm
4cm
6cm
4cm
12cm
8cm
做一做
解:图(1)中,三组对应角分别是 ,并且对应边的比都是2
45°、45°、90°
图(2)中,三组对应角分别是 ,并且对应边的比都是
.所以每组中的两个三角形是相似的.
30°、60°、90°
分析:分析三角板各角的度数,并测量各边,再依据定义判断.
应用新知
巩固新知
课堂小结
布置作业
2.如图,已知直线BC平行DE,△ABC与△ADE相似吗?
探究新知
创设情境
A
B
C
D
E
4
4
4
4
3
6
解:∵直线BC平行DE
∴∠ABC=∠ADE,
∠ACB=∠AED,
∠A=∠A,
又∵AB=4, AC=4, BC=3,
AD=4+4=8, AE=4+4=8, DE=6,
所以,根据相似三角形的定义可得, △ABC与△ADE相似
注意:相似用符号“∽”表示,如△ABC与△ADE相似记为: △ABC ∽ △ADE
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
A
B
C
A'
B'
C'
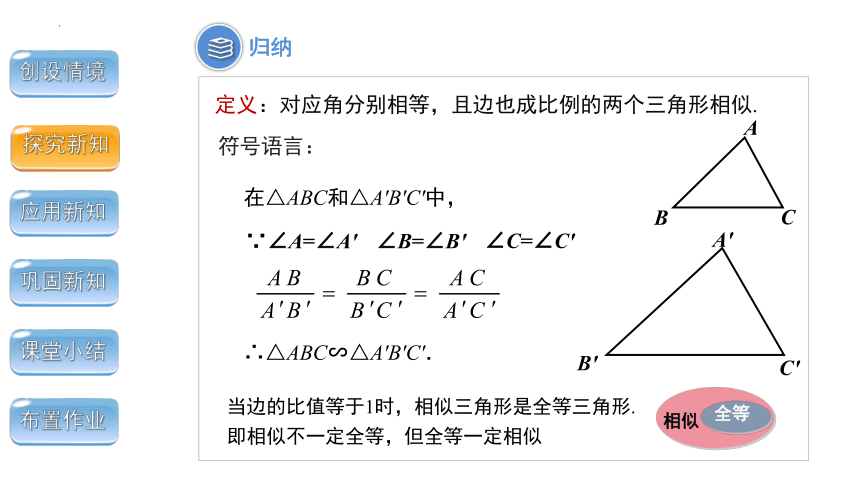
符号语言:
在△ABC和△A'B'C'中,
∴△ABC∽△A'B'C'.
∵∠A=∠A'
∠B=∠B'
∠C=∠C'
定义:对应角分别相等,且边也成比例的两个三角形相似.
归纳
当边的比值等于1时,相似三角形是全等三角形.
即相似不一定全等,但全等一定相似
相似
全等
应用新知
巩固新知
课堂小结
布置作业
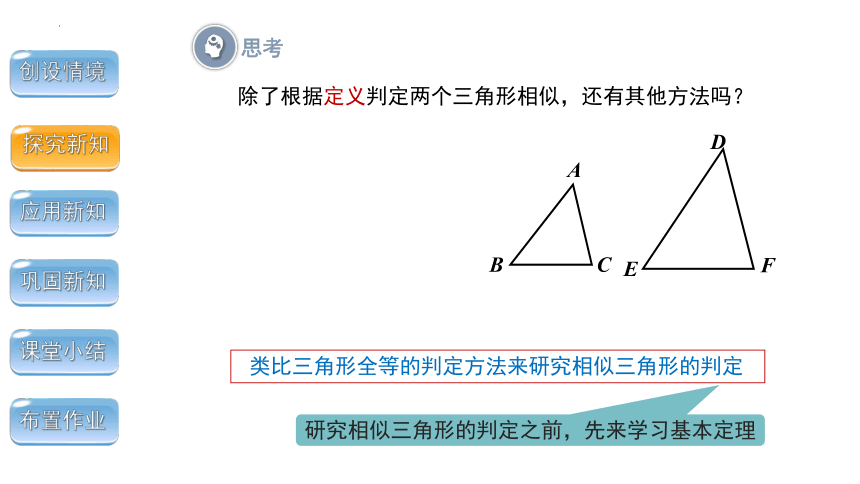
除了根据定义判定两个三角形相似,还有其他方法吗?
探究新知
创设情境
C
A
B
D
E
F
思考
类比三角形全等的判定方法来研究相似三角形的判定
研究相似三角形的判定之前,先来学习基本定理
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
探究
A
B
C
D
E
F
ED=2cm,
FE=5cm
AB=2cm,
BC=5cm
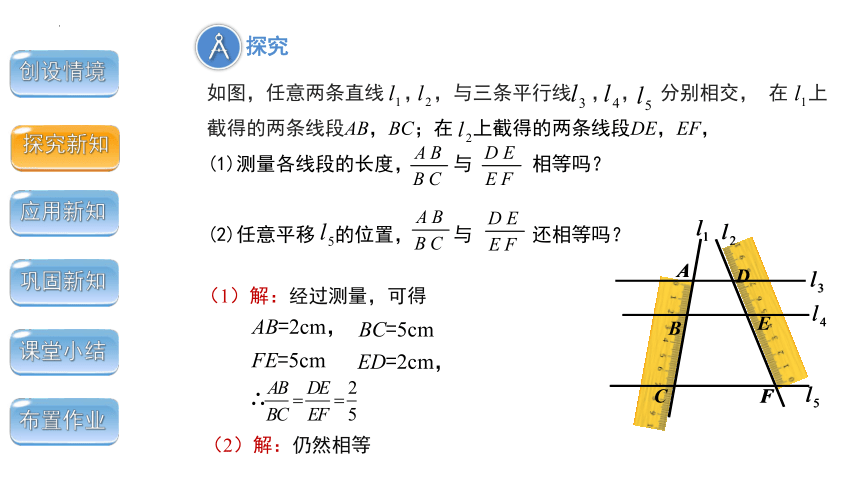
(1)解:经过测量,可得
(2)解:仍然相等
如图,任意两条直线 , ,与三条平行线 , , 分别相交, 在 上截得的两条线段AB,BC;在 上截得的两条线段DE,EF,
(1)测量各线段的长度, 与 相等吗?
(2)任意平移 的位置, 与 还相等吗?
A
B
C
D
E
F
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
探究
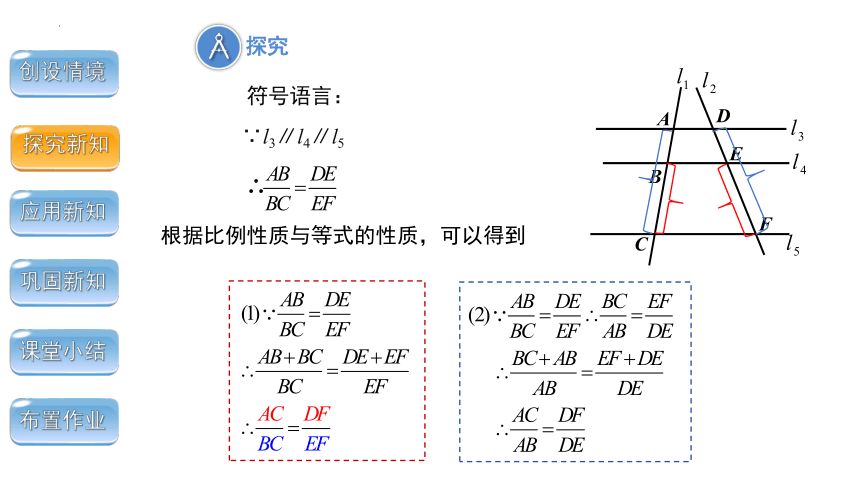
根据比例性质与等式的性质,可以得到
A
B
C
D
E
F
符号语言:
∵l3∥l4∥l5
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
形成结论
A
B
C
D
E
F
符号语言:
∵l3∥l4∥l5
基本事实
两条直线被一组平行线所截,所得的对应线段成比例.
总结:对应线段分为三组,可得,最长线段:AC、DF;
上边的线段: AB、DE;下边的线段:BC、EF;
共三组
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
∵l3∥l4∥l5
根据等比性质,上述比例也可以写成:
基本事实延伸
A
B
C
D
E
F
技巧总结:在基本事实中,只要有一个比例式成立,剩余的比例式都 成立.对应线段的位置可以是某个分式的分子分母,也可以分别是两个分式的分母或分子
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
A
B
C
E
D
基本事实应用
右图中,当直线 与 相交时,
基本事实还成立吗?涂色的两个
三角形相似吗?
分析:成立.对应边仍然成比例,即
由基本事实,可得 ,由两直线平行,同位角相等,以及∠A是公共角.
如果能够说明CF、BE的比值也等于 ,即可说明三角形相似.
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
证明
如图,在△ABC中,DE//BC,且DE分别交AB,AC于点D,E,△ADE与△ABC相似吗?说明理由.
分析:△ADE与△ABC相似.
借助基本事实来证明,
依据三角形相似的定义来说明相似.
A
B
C
D
E
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
证明
过点E作EF∥AB,交BC于点F.
A
B
C
D
E
F
证明:在△ADE与△ABC中,∠A=∠A.
∵DE∥BC,∴∠ADE=∠B,∠AED=∠C.
注意:在相似比中,对应边的位置要正确
∵DE ∥ BC,
∴
又∵EF∥AB,
∴ ,
又∵四边形DEFB是平行四边形,∴BF=DE
∴ .
∴△ADE∽△ABC(相似三角形的定义)
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
上述证明过程的辅助线,还有其他做法吗?
A
B
C
D
E
反思
A
B
C
D
E
F
A
B
C
D
E
H
还有一种辅助线的做法
A
B
C
D
E
(基本事实)
两直线平行,
同位角相等
∠A=∠A.
∠ADE=∠B,
∠AED=∠C.
添加辅助线
再次借助基本事实
A
B
C
D
E
H
△ADE∽△ABC
证明逻辑顺序:
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
归纳
预备定理:
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
如图:∵DE∥BC
A
B
C
D
E
∴△ADE∽△ABC
目前证明三角形相似的方法有:
定义法、平行线法
通过右边图形证明三角形相似的方法,也称为平行线法
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
例1
如图,在△ABC中,DE∥BC,AD=EC,DB=1 cm,AE=4 cm,BC=5 cm,求DE的长.
解:∵DE∥BC,
∴△ADE∽△ABC.
∴
又AD=EC,DB=1 cm,AE=4 cm,
∴
∴AD=2.又
BC=5 cm,
∴ ,
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
1.如图,DE∥BC,EF∥AB,则下列式子错误的是( ).
D.
A.
B.
C.
D
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
2.如图,点E是平行四边形ABCD的边BC延长线上的一点,
连接AE交CD于点F,则图中共有相似三角形( ).
A.1对 B.2对 C.3对 D.4对
C
总结:图形的相似具有传递性
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
3.如图,AB∥CD∥EF,AF与BE相交于点G,
且AG=2,GD=1,DF=5,则 .
C
E
B
A
F
D
G
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
判定相似三角形的方法汇总
基本事实
平行线法
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
证明方法:添加辅助线,两次利用基本事实
基本事实
两条直线被一组平行线所截,所得的对应线段成比例.
探究过程:观察加试验
A
B
C
D
E
A
B
C
D
E
F
定义法(三条边,三个角都要满足条件)
平行线法(三角形中出现平行线即可)
布置作业
教科书习题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
27.2.1 相似三角形的判定
——基本事实及其应用
学习目标
掌握相似三角形的定义和性质,明确定义是第一种判定方法;
掌握基本事实,并能够迁移到三角形中,得到对应结论;
利用基本事实证明平行于三角形一边的直线截取的两个三角形相似;
4. 探究经历“试验、猜想、证明”的过程,感受几何命题的合理性,并通过证明确认命题正确,培养学生发现问题、解决问题的能力.
重点
基本事实
难点
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
我们已经学过了相似图形、相似多边形的定义,你能得到相似三角形的定义吗?
复习回顾
相似图形:形状相同的图形
相似图形
相似五边形
相似多边形:边数相同,角分别相等,并且边也成比例的两个多边形
相似三角形:对应角分别相等,并且边也成比例的两个三角形
类比
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
1.下图中,你能利用定义判定每组中的两个三角形相似吗?
(1)
(2)
8cm
4cm
8cm
4cm
6cm
4cm
12cm
8cm
做一做
解:图(1)中,三组对应角分别是 ,并且对应边的比都是2
45°、45°、90°
图(2)中,三组对应角分别是 ,并且对应边的比都是
.所以每组中的两个三角形是相似的.
30°、60°、90°
分析:分析三角板各角的度数,并测量各边,再依据定义判断.
应用新知
巩固新知
课堂小结
布置作业
2.如图,已知直线BC平行DE,△ABC与△ADE相似吗?
探究新知
创设情境
A
B
C
D
E
4
4
4
4
3
6
解:∵直线BC平行DE
∴∠ABC=∠ADE,
∠ACB=∠AED,
∠A=∠A,
又∵AB=4, AC=4, BC=3,
AD=4+4=8, AE=4+4=8, DE=6,
所以,根据相似三角形的定义可得, △ABC与△ADE相似
注意:相似用符号“∽”表示,如△ABC与△ADE相似记为: △ABC ∽ △ADE
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
A
B
C
A'
B'
C'
符号语言:
在△ABC和△A'B'C'中,
∴△ABC∽△A'B'C'.
∵∠A=∠A'
∠B=∠B'
∠C=∠C'
定义:对应角分别相等,且边也成比例的两个三角形相似.
归纳
当边的比值等于1时,相似三角形是全等三角形.
即相似不一定全等,但全等一定相似
相似
全等
应用新知
巩固新知
课堂小结
布置作业
除了根据定义判定两个三角形相似,还有其他方法吗?
探究新知
创设情境
C
A
B
D
E
F
思考
类比三角形全等的判定方法来研究相似三角形的判定
研究相似三角形的判定之前,先来学习基本定理
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
探究
A
B
C
D
E
F
ED=2cm,
FE=5cm
AB=2cm,
BC=5cm
(1)解:经过测量,可得
(2)解:仍然相等
如图,任意两条直线 , ,与三条平行线 , , 分别相交, 在 上截得的两条线段AB,BC;在 上截得的两条线段DE,EF,
(1)测量各线段的长度, 与 相等吗?
(2)任意平移 的位置, 与 还相等吗?
A
B
C
D
E
F
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
探究
根据比例性质与等式的性质,可以得到
A
B
C
D
E
F
符号语言:
∵l3∥l4∥l5
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
形成结论
A
B
C
D
E
F
符号语言:
∵l3∥l4∥l5
基本事实
两条直线被一组平行线所截,所得的对应线段成比例.
总结:对应线段分为三组,可得,最长线段:AC、DF;
上边的线段: AB、DE;下边的线段:BC、EF;
共三组
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
∵l3∥l4∥l5
根据等比性质,上述比例也可以写成:
基本事实延伸
A
B
C
D
E
F
技巧总结:在基本事实中,只要有一个比例式成立,剩余的比例式都 成立.对应线段的位置可以是某个分式的分子分母,也可以分别是两个分式的分母或分子
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
A
B
C
E
D
基本事实应用
右图中,当直线 与 相交时,
基本事实还成立吗?涂色的两个
三角形相似吗?
分析:成立.对应边仍然成比例,即
由基本事实,可得 ,由两直线平行,同位角相等,以及∠A是公共角.
如果能够说明CF、BE的比值也等于 ,即可说明三角形相似.
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
证明
如图,在△ABC中,DE//BC,且DE分别交AB,AC于点D,E,△ADE与△ABC相似吗?说明理由.
分析:△ADE与△ABC相似.
借助基本事实来证明,
依据三角形相似的定义来说明相似.
A
B
C
D
E
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
证明
过点E作EF∥AB,交BC于点F.
A
B
C
D
E
F
证明:在△ADE与△ABC中,∠A=∠A.
∵DE∥BC,∴∠ADE=∠B,∠AED=∠C.
注意:在相似比中,对应边的位置要正确
∵DE ∥ BC,
∴
又∵EF∥AB,
∴ ,
又∵四边形DEFB是平行四边形,∴BF=DE
∴ .
∴△ADE∽△ABC(相似三角形的定义)
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
上述证明过程的辅助线,还有其他做法吗?
A
B
C
D
E
反思
A
B
C
D
E
F
A
B
C
D
E
H
还有一种辅助线的做法
A
B
C
D
E
(基本事实)
两直线平行,
同位角相等
∠A=∠A.
∠ADE=∠B,
∠AED=∠C.
添加辅助线
再次借助基本事实
A
B
C
D
E
H
△ADE∽△ABC
证明逻辑顺序:
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
归纳
预备定理:
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
如图:∵DE∥BC
A
B
C
D
E
∴△ADE∽△ABC
目前证明三角形相似的方法有:
定义法、平行线法
通过右边图形证明三角形相似的方法,也称为平行线法
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
例1
如图,在△ABC中,DE∥BC,AD=EC,DB=1 cm,AE=4 cm,BC=5 cm,求DE的长.
解:∵DE∥BC,
∴△ADE∽△ABC.
∴
又AD=EC,DB=1 cm,AE=4 cm,
∴
∴AD=2.又
BC=5 cm,
∴ ,
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
1.如图,DE∥BC,EF∥AB,则下列式子错误的是( ).
D.
A.
B.
C.
D
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
2.如图,点E是平行四边形ABCD的边BC延长线上的一点,
连接AE交CD于点F,则图中共有相似三角形( ).
A.1对 B.2对 C.3对 D.4对
C
总结:图形的相似具有传递性
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
3.如图,AB∥CD∥EF,AF与BE相交于点G,
且AG=2,GD=1,DF=5,则 .
C
E
B
A
F
D
G
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
判定相似三角形的方法汇总
基本事实
平行线法
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
证明方法:添加辅助线,两次利用基本事实
基本事实
两条直线被一组平行线所截,所得的对应线段成比例.
探究过程:观察加试验
A
B
C
D
E
A
B
C
D
E
F
定义法(三条边,三个角都要满足条件)
平行线法(三角形中出现平行线即可)
布置作业
教科书习题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
