数学人教A版(2019)必修第一册5.2.1三角函数的概念 课件（共36张ppt）

(共36张PPT)
5.2.1 三角函数的概念
学
习
目
标
1.理解三角函数的概念，会求给定角的三角函数值.
2.掌握各象限角的三角函数值的符号规律.
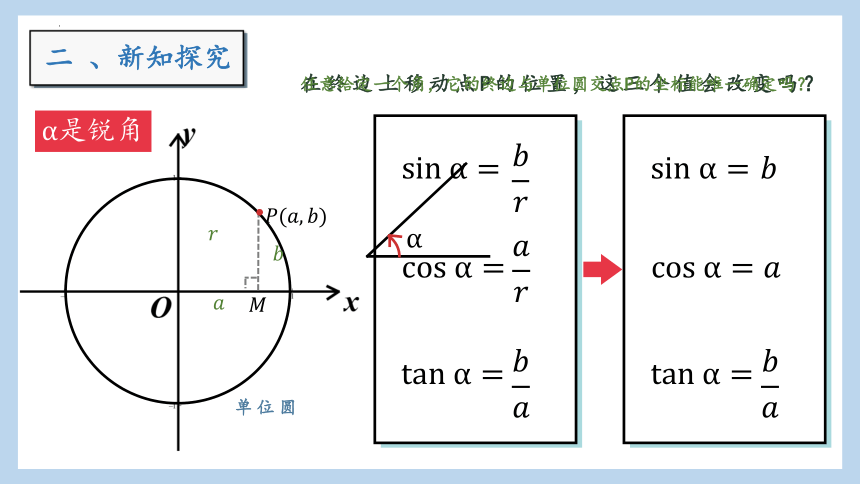
知识回顾：在初中时我们是如何定义锐角三角函数的呢？
？
？
？
O
a
b
A
P
c
二 、新知探究
上述定义只限于直角三角形中的锐角，
而现在角的定义已经拓广到任意角，如:
？
？
？
锐角三角函数
任意角三角函数
是锐角
二 、新知探究
在终边上移动点P的位置，这三个值会改变吗？
单位圆
任意给定一个角，它的终边与单位圆交点P的坐标能唯一确定吗？
任意角的三角函数
设是一个任意角，，它的终边与单位圆相交于点.
(1)把点 的纵坐标 叫做的正弦函数(),记作，即
(2)把点 的横坐标 叫做的余弦函数(),记作，即
(3)把点 的纵坐标与横坐标的比值 叫做的正切，记作，即
任意角的三角函数
我们将正弦函数、余弦函数和正切函数统称为三角函数（trigonometric function），通常将它们记为：
正弦函数
余弦函数
正切函数

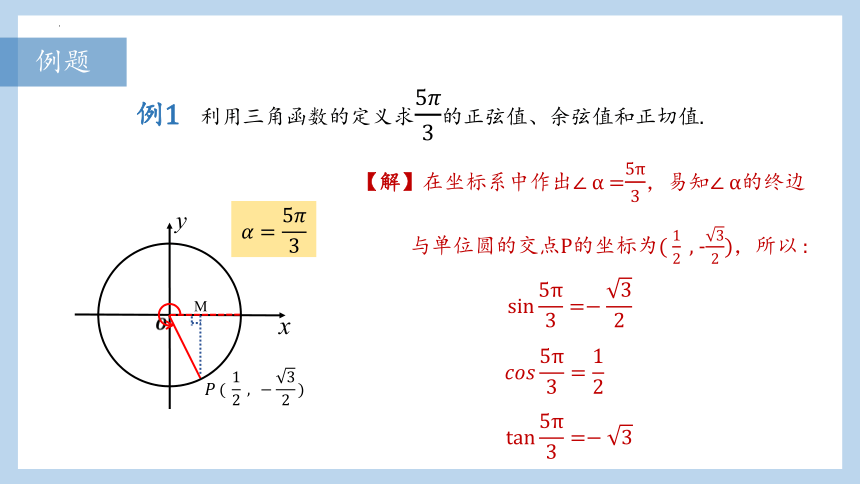
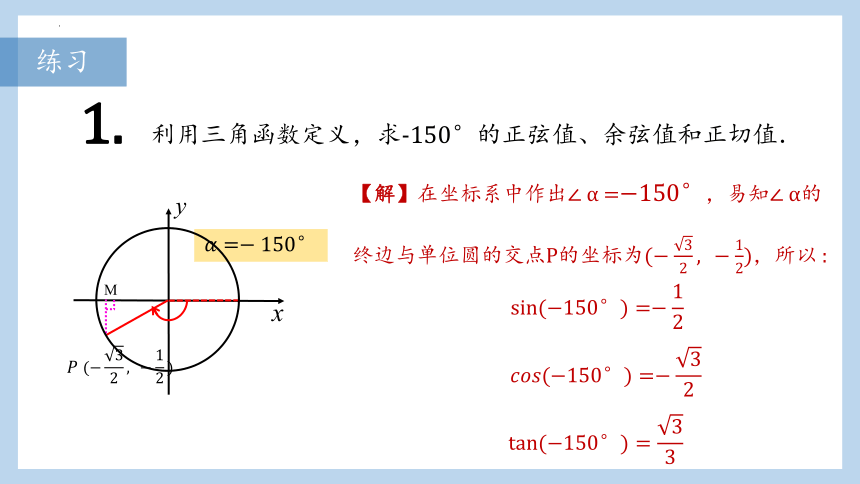
【解】在坐标系中作出∠ =，易知∠ 的终边
与单位圆的交点P的坐标为( , -)，所以 :
例1 利用三角函数的定义求的正弦值、余弦值和正切值.
例题
归纳
利用单位圆求任意角三角函数值的一般步骤
①把角放在平面直角坐标系中
②画出直角三角形
③求出角的终边与单位圆的交点坐标
④利用定义来确定三角函数的值
【解】在坐标系中作出∠ =，易知∠ 的终边与单位圆的交点P的坐标为()，所以 :
1. 利用三角函数定义，求-150°的正弦值、余弦值和正切值．
练习
练习
2. 已知角的终边经过点，求角的正弦、余弦和正切值 .
三 、定义推广
设角是一个任意角，是终边上的任意一点，点与原点的距离
那么① 叫做的正弦，即 ;
② 叫做的余弦，即 ;
③ 叫做的正切，即 () .
任意角的三角函数值仅与有关，而与点在角的终边上的位置无关.
练习
2. 已知角的终边经过点，求角的正弦、余弦和正切值 .
【解】
=
，
，
=5，
=
=
推广
;
;
() .
-
-
+
+
四 、符号规律
+
-
-
+
-
+
-
+
一全正，二正弦，三正切，四余弦
练习
练习
思考：终边相同的角的同一三角函数值有什么关系？
五 、终边相同的角
终边相同的角的同名三角函数值相等。
六 、特殊角的三角函数
角度α
角α的
弧度数
180°
270°
360°
不存在
不存在
七 、课堂小结
(1)把点 的纵坐标 叫做的正弦函数(),记作，即
(2)把点 的横坐标 叫做的余弦函数(),记作，即
(3)把点 的纵坐标与横坐标的比值 叫做的正切，记作，即
1.三角函数的概念：
2.符号规律：
一全正，二正弦，三正切，四余弦
推广
;
;
() .
八 、课后作业
1.《优化方案》5.2.1 三角函数的概念
2.思考：终边相同的角的同一三角函数值有什么关系？
探究点一 求任意角的三角函数值
例1（1） 已知角 的终边与单位圆的交点坐标为 ，则 ____.

[解析] 角 的终边与单位圆的交点坐标为 ， ，即
， 或 .当 时， ， ，则
；当 时， ， ，则
.综上可得， .
（2）利用定义求 的正弦、余弦和正切值.
解：如图所示，设坐标原点为 ， 角的终边与单位圆的交点
为 ，过点 作 轴交 轴于点 .在 中，
， ，则 ， ，
，
故 ， ， .
［素养小结］
利用三角函数的定义求一个角的三角函数值有以下几种情况：
（1）若已知角，则只需确定出该角的终边与单位圆的交点坐标，即可求出各三角函数值.
（2）若已知角 终边上一点 是单位圆上一点，则 ，
， .
（3）若已知角 终边上一点 不是单位圆上一点，则先求
，再求 ， , .
（4）若已知角 终边上的点的坐标含参数，则要根据问题的实际情况对参数进
行分类讨论.
探究点二 判断三角函数值的符号
例2（1） （多选题）下列选项中，符号为负的是( )
ABD
A. B. C. D.
[解析] 角是第三象限角，故 ； 角是第二象限角，
故 ； ， 是第三象限角，故 ；
.故选 .
（2）[2022·西工大附中高一月考] 若 是第四象限角，则点 在
( )
C
A.第四象限 B.第三象限 C.第三或第四象限 D.第一或第二象限
[解析] 因为 是第四象限角，所以 , ，则
, .当 是奇数时， 是第二象限角，则 ,
，所以点 在第三象限；当 是偶数时， 是第四象限角，则
, ，所以点 在第四象限.综上可得，点 在第三或第四象限.
故选C.
［素养小结］
判断三角函数值在各象限的符号的攻略：
（1）基础：准确确定三角函数值中各角所在象限；
（2）关键：准确记忆三角函数值在各象限的符号；
（3）注意：用弧度制给出的角常常不写单位，不要误认为角度,导致象限判断错误.
探究点三 求三角函数的定义域
例3 求下列函数的定义域:
（1） ;
解： 要使函数有意义, 必须使 与 都有意义,
所以 所以函数 的定义域为
.
（2） .
解： 要使函数有意义,必须使 有意义,且 ,所以
，
所以函数 的定义域为 .
［素养小结］
（1）解题时要注意函数本身的隐含条件.
（2）求三角函数的定义域,应熟悉各三角函数在各象限内的符号,并要注意各三角函数的定义域,一般用弧度制表示.
探究点四 公式一的应用
例4（1） ( )
B
A. B. C. D.
[解析] .故选B.
（2） ( )
C
A. B. C. D.
[解析] .故选C.
（3） _ _.

[解析] 原式 .
（4） ___.
0
[解析] 原式 .
［素养小结］
利用公式一进行化简求值的步骤：
（1）定形：将已知的任意角写成 的形式，其中 ， .
（2）转化：根据公式一，转化为求角 的某个三角函数值.
（3）求值：若角 为特殊角，则可直接求出该角的三角函数值（需熟记特殊角的三角函数值）.
例题
例2 已知角的终边经过点，求角的正弦、余弦和正切值 .

【解】
= ,
= ,
= ,
设角的终边与单位圆交于点.
分别过点，作轴的垂线, ，垂足分别为，，则：
11
例题
例3 若是第三象限角，则下列结论正确的是（ ）
A. 0
B. 0
C. 0
例4 若是第二象限角，则下列结论正确的是（ ）
A. 0
B. 0
C. 0
例5 若是第四象限角，则下列结论正确的是（ ）
A. 0
B. 0
C. 0
16