数学人教A版(2019)必修第一册4.2.1指数函数的概念 课件(共38张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册4.2.1指数函数的概念 课件(共38张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 11.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-29 09:37:10 | ||
图片预览






文档简介
(共38张PPT)
4.2.1 指数函数的概念
2023级高一课前准备
1.课本111页,学案,笔记本,草稿纸
2.回忆“幂函数”及“指数幂的运算”的相关知识
3.动脑,动手,动笔,积极发言
温故知新
对于幂ax(a>0),我们已经把指数的范围拓展到了任意实数,通过函数性质的学习和对幂函数的研究,我们掌握了研究函数的一般方法:
背景
概念
图像与性质
应用
本章,我们将学习两个基本初等函数——指数函数和对数函数。今天我们学习指数函数。
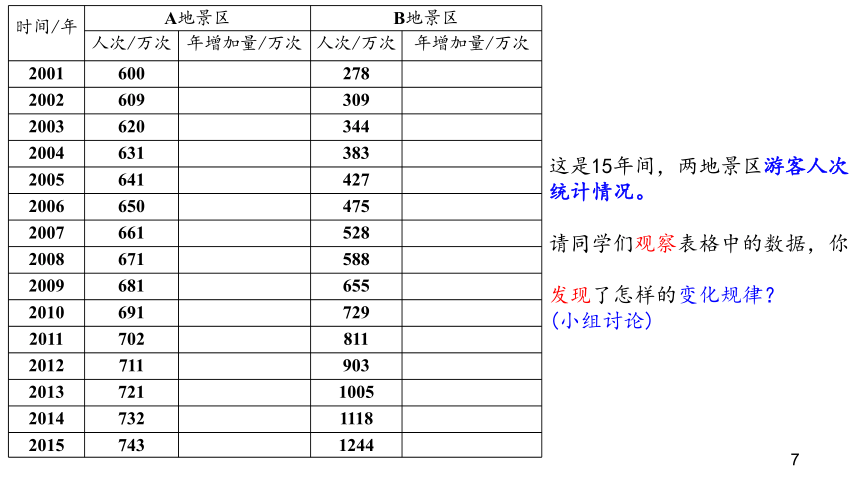
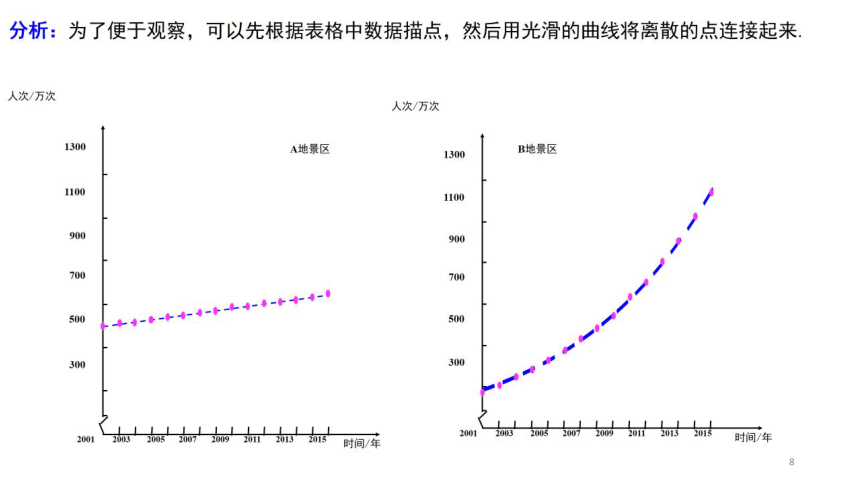
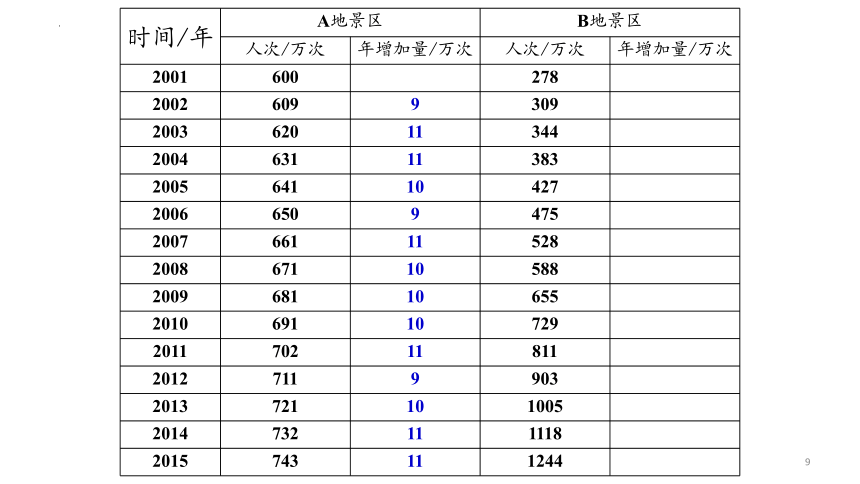
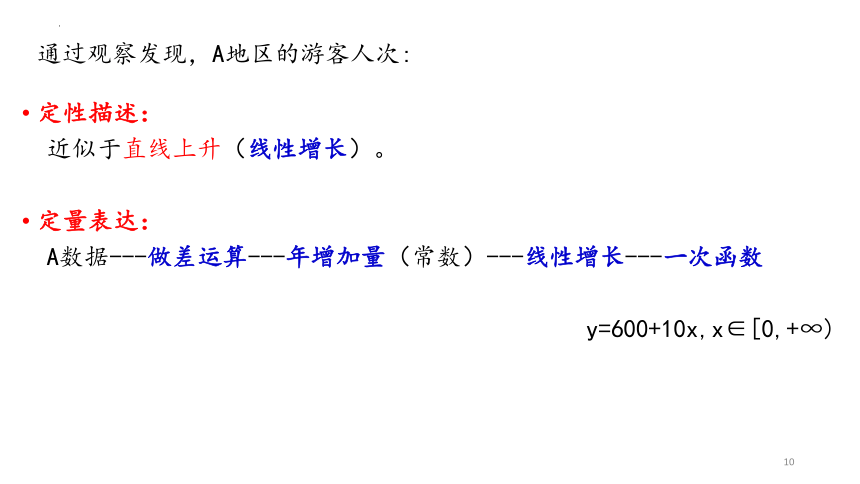
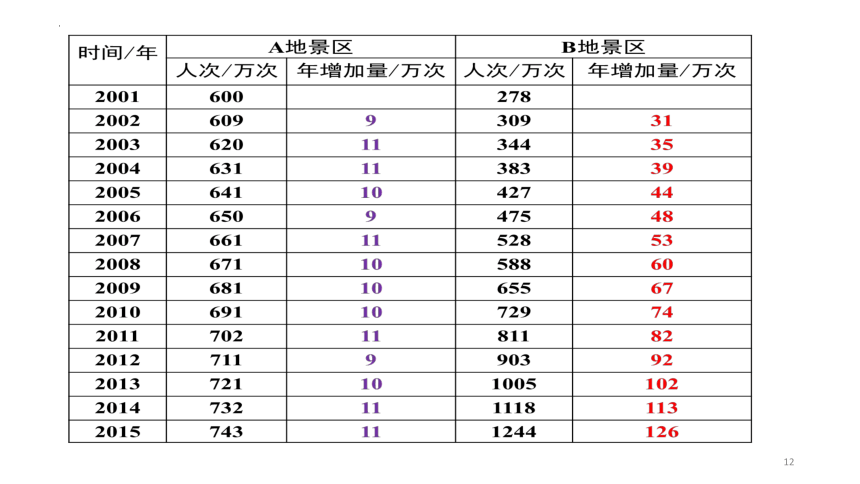
问题探究问题1:随着中国经济高速增长,人民生活水平不断提高,旅游成了越来越多家庭的重要生活方式.由于旅游人数不断增加,A,B两地景区自2001年起采取了不同的应对措施,A地提高了景区门票价格,而B地则取消了景区门票.下表给出了A,B两地景区2001年至2015年的游客人次统计情况:时间/年A地景区B地景区人次/万次年增加量/万次人次/万次年增加量/万次200160027820026093092003620344200463138320056414272006650475200766152820086715882009681655201069172920117028112012711903201372110052014732111820157431244这是15年间,两地景区游客人次统计情况。请同学们观察表格中的数据,你发现了怎样的变化规律?(小组讨论)时间/年A地景区B地景区人次/万次年增加量/万次人次/万次年增加量/万次20016002782002609930931200362011344352004631113833920056411042744200665094754820076611152853200867110588602009681106556720106911072974201170211811822012711990392201372110100510220147321111181132015743111244126这是15年间,两地景区游客人次的变化情况请同学们观察表格中的数据,你发现了怎样的变化规律?时间/年A地景区B地景区人次/万次年增加量/万次人次/万次年增加量/万次2001600278200260993092003620113442004631113832005641104272006650947520076611152820086711058820096811065520106911072920117021181120127119903201372110100520147321111182015743111244通过观察发现,A地区的游客人次:定性描述:近似于直线上升(线性增长)。定量表达:A数据---做差运算---年增加量(常数)---线性增长---一次函数y=600+10x,x∈[0,+∞)定性描述:B景区的游客人次则是----非线性增长,那么,你能不能类比对数据A的研究方法,找到一个揭示它们之间不变关系的量,进而对其进行定量刻画呢?大家有什么想法?定量表达:?(似乎无头绪)----------从2002年起,将B景点每年的游客人次除以上一年的游客人次,可得: ……. 1.111.111.11探究结论:(1)B景区的游客人次的年增长率都约为0.11.(2)增长率为常数的变化方式,我们称为指数增长。B景区的游客人次近似于指数增长B景区:从2001年开始,B景区游客人次的变化规律可以近似的描述为1年后,游客人次是2001年的1.11倍;2年后,游客人次是2001年的1.11 倍;3年后,游客人次是2001年的1.11 倍;··· ··· ··· ···设经过x年后的游客人次是2001年的y倍,则y=1.11x,x∈[0,+∞).这是一个函数,其中指数x是自变量.y=(1+0.11)x,x∈[0,+∞)定性描述:B景区的游客人次----非线性增长,年增长量越来越大,定量表达:B数据---做商运算---年增长率(常数)---指数增长---新函数y=1.11x,x∈[0,+∞)A数据----做差运算----年增加量(常数)----线性增长----一次函数y=600+10x,x∈[0,+∞)B数据----做商运算----年增长率(常数)----指数增长----新函数y=1.11x,x∈[0,+∞)良渚遗址位于浙江省杭州市余杭区良渚镇,1936年首次发现.这里的巨型城址,面积近300万平方米,包括古城、水坝和多处高等级建筑.考古学家测定,古城存在时期为公元前3300年~前2500年.你知道考古学家是怎么测出这个时间的吗?碳14检测法问题2:当生物死亡后,它机体内原有的碳14会按确定的比例衰减(称为衰减率),大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.按照上述变化规律,生物体内碳14含量与死亡年数之间有怎样的关系?设死亡生物体内碳14含量的年衰减率为p,我们把刚死亡生物体内碳14含量看成1个单位,那么死亡1年后, 生物体内碳14的含量为1-1·p=1-p;死亡2年后, 生物体内碳14的含量为(1-p)-(1-p)·p=(1-p) ;死亡3年后, 生物体内碳14的含量为(1-p) -(1-p) ·p=(1-p) ;··· ··· ··· ···死亡5730年后, 生物体内碳14的含量为(1-p)5730;死亡x年后, 生物体内碳14的含量为(1-p)xy=(1-p)x,x∈[0,+∞)根据已知,所以(常数)设生物死亡年数为x,死亡生物体内碳14含量为y,则即这也是一个函数,指数x是自变量.碳14每年以 的衰减率衰减.像这样,衰减率为常数的变化方式,我们称为指数衰减。细胞分裂y=2x,x∈N*《庄子·天下篇》中写道:“一尺之棰,日取之半,万世不竭” 把一张纸对折……一张纸很普通?科学家:如果将它对折103次……超出宇宙的可观测直径930亿光年总结:(1)y=1.11x,x∈[0,+∞)(2)(3)y=2x,∈N* y=ax指数x是自变量指 数 函 数的 概 念:一般地,函数y=ax(a>0且a≠1)叫做指数函数,其中指数x是自变量,定义域是R.
0
1
a
为什么规定呢?
若
若
0的正分数指数幂等于0,0的负分数指数幂没有意义
函数形式上有什么特征?
因此,指数函数的定义只是一个形式定义.判断一个函数是不是指数函数关键是看这个函数的解析式变形整理之后是不是具备以上三个特征.
典例探究:典例1: 判断下列函数那些是指数函数?① y=-2x; ②y=(-2)x; ③y=(2)-x;④y=2x-1;⑤y=2x(x>0);⑥y=(m-1)x(m>1,m≠2的常数);⑦y=x2;⑧y=2x+1;⑨y=3·2x;答:③⑥是指数函数,其余都不是.典例2: 已知指数函数f(x)=ax(a>0,且a≠1),且f(3)=π,求:f(0),f(1),f(-3)值.解:∵f(x)=ax,且f(3)=π, 则a3=π, 解得∴∴方法总结:待定系数法确定指数函数解析式典例3(1)如果平均每位游客出游一次可给当地带来1000元门票之外的收入,A地景区的门票价格为150元,比较这15年间A,B两地旅游收入变化情况.解:设经过x年,游客给A、B两地带来的收入分别为f(x),g(x),则g(x)=1000×278×1.11x利用计算工具可以算出:当x=0时,f(0)-g(0)=412 000.当x≈10.22时,f(10.22)≈g(10.22).结合右图可知:当x>10.22时,f(x)<g(x).当x<10.22时,f(x)>g(x).当x=14时,g(14)-f(14)≈347 303.答:(1)2001年,游客给A地带来的收入高于B地412000万元;(2)2001后的10年,f(x)>g(x),游客给A地带来的收入仍高于B地,但g(x)比f(x)增长的速度快,大约2011年2月某个时刻就有f(x)=g(x)了,这时游客给A地带来的收入和B地差不多;(3)10年后,f(x)<g(x),游客给B地带来的收入高于了A地,由于g(x)增长的速度越来越快,而f(x)增长的速度不变,到2015年,游客给B地带来的收入已经高于了A地347303万元了.在问题(2)中,某生物死亡10000年后,它体内碳14的含量衰减为原来的百分之几? 在实际问题中,经常会遇到类似于例题3中的指数增长模型:设原有量为N,每次的增长率为p,经过x次增长,该量增长到y,则y=N(1+p)x,x∈N.形如y=kax(k∈R,且k≠0,a>0,且a≠1)的函数是刻画指数增长或指数衰减变化规律的非常有用的函数模型.课堂练习:1.函数y=(2a-3)ax是指数函数,则f(1)=( ) 答案:D2.已知函数f(x)=(2a-1)x是指数函数,则a的取值范围是______ 3.随着我国经济的不断发展,2014年年底某偏远地区的农民人均年收入为3000元,预计该地区今后的农民的人均年收入将以6%的平均增长率增加,那么2021年年底该地区的农民人均年收入为( ) 答案:B4.调查表明:酒后驾驶是导致交通事故的主要原因,交通法规规定:驾驶员在驾驶机动车时,血液中的酒精含量不得超过0.2mg/ml,如果某人喝了少量酒后,血液中的酒精含量将迅速上升到0.8mg/ml,在停止喝酒后,血液中的酒精含量将以每小时50%的速度减少,则他至少经过多少小时后才可以驾驶机动车 解:设经过x个小时后才可以驾驶机动车,由题意得,【归纳小节】
1.指数函数的定义
一般的,函数 叫做指数函数,其中指数是自变量,定义域是R
2.指数函数形式上有什么特征
3.理解指数函数模型。
分层作业2:三二小本261页,营养提升练
10题,11题。(选做)
分层作业1:三二大本任务学习一和二。(必做)
4.2.1 指数函数的概念
2023级高一课前准备
1.课本111页,学案,笔记本,草稿纸
2.回忆“幂函数”及“指数幂的运算”的相关知识
3.动脑,动手,动笔,积极发言
温故知新
对于幂ax(a>0),我们已经把指数的范围拓展到了任意实数,通过函数性质的学习和对幂函数的研究,我们掌握了研究函数的一般方法:
背景
概念
图像与性质
应用
本章,我们将学习两个基本初等函数——指数函数和对数函数。今天我们学习指数函数。
问题探究问题1:随着中国经济高速增长,人民生活水平不断提高,旅游成了越来越多家庭的重要生活方式.由于旅游人数不断增加,A,B两地景区自2001年起采取了不同的应对措施,A地提高了景区门票价格,而B地则取消了景区门票.下表给出了A,B两地景区2001年至2015年的游客人次统计情况:时间/年A地景区B地景区人次/万次年增加量/万次人次/万次年增加量/万次200160027820026093092003620344200463138320056414272006650475200766152820086715882009681655201069172920117028112012711903201372110052014732111820157431244这是15年间,两地景区游客人次统计情况。请同学们观察表格中的数据,你发现了怎样的变化规律?(小组讨论)时间/年A地景区B地景区人次/万次年增加量/万次人次/万次年增加量/万次20016002782002609930931200362011344352004631113833920056411042744200665094754820076611152853200867110588602009681106556720106911072974201170211811822012711990392201372110100510220147321111181132015743111244126这是15年间,两地景区游客人次的变化情况请同学们观察表格中的数据,你发现了怎样的变化规律?时间/年A地景区B地景区人次/万次年增加量/万次人次/万次年增加量/万次2001600278200260993092003620113442004631113832005641104272006650947520076611152820086711058820096811065520106911072920117021181120127119903201372110100520147321111182015743111244通过观察发现,A地区的游客人次:定性描述:近似于直线上升(线性增长)。定量表达:A数据---做差运算---年增加量(常数)---线性增长---一次函数y=600+10x,x∈[0,+∞)定性描述:B景区的游客人次则是----非线性增长,那么,你能不能类比对数据A的研究方法,找到一个揭示它们之间不变关系的量,进而对其进行定量刻画呢?大家有什么想法?定量表达:?(似乎无头绪)----------从2002年起,将B景点每年的游客人次除以上一年的游客人次,可得: ……. 1.111.111.11探究结论:(1)B景区的游客人次的年增长率都约为0.11.(2)增长率为常数的变化方式,我们称为指数增长。B景区的游客人次近似于指数增长B景区:从2001年开始,B景区游客人次的变化规律可以近似的描述为1年后,游客人次是2001年的1.11倍;2年后,游客人次是2001年的1.11 倍;3年后,游客人次是2001年的1.11 倍;··· ··· ··· ···设经过x年后的游客人次是2001年的y倍,则y=1.11x,x∈[0,+∞).这是一个函数,其中指数x是自变量.y=(1+0.11)x,x∈[0,+∞)定性描述:B景区的游客人次----非线性增长,年增长量越来越大,定量表达:B数据---做商运算---年增长率(常数)---指数增长---新函数y=1.11x,x∈[0,+∞)A数据----做差运算----年增加量(常数)----线性增长----一次函数y=600+10x,x∈[0,+∞)B数据----做商运算----年增长率(常数)----指数增长----新函数y=1.11x,x∈[0,+∞)良渚遗址位于浙江省杭州市余杭区良渚镇,1936年首次发现.这里的巨型城址,面积近300万平方米,包括古城、水坝和多处高等级建筑.考古学家测定,古城存在时期为公元前3300年~前2500年.你知道考古学家是怎么测出这个时间的吗?碳14检测法问题2:当生物死亡后,它机体内原有的碳14会按确定的比例衰减(称为衰减率),大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.按照上述变化规律,生物体内碳14含量与死亡年数之间有怎样的关系?设死亡生物体内碳14含量的年衰减率为p,我们把刚死亡生物体内碳14含量看成1个单位,那么死亡1年后, 生物体内碳14的含量为1-1·p=1-p;死亡2年后, 生物体内碳14的含量为(1-p)-(1-p)·p=(1-p) ;死亡3年后, 生物体内碳14的含量为(1-p) -(1-p) ·p=(1-p) ;··· ··· ··· ···死亡5730年后, 生物体内碳14的含量为(1-p)5730;死亡x年后, 生物体内碳14的含量为(1-p)xy=(1-p)x,x∈[0,+∞)根据已知,所以(常数)设生物死亡年数为x,死亡生物体内碳14含量为y,则即这也是一个函数,指数x是自变量.碳14每年以 的衰减率衰减.像这样,衰减率为常数的变化方式,我们称为指数衰减。细胞分裂y=2x,x∈N*《庄子·天下篇》中写道:“一尺之棰,日取之半,万世不竭” 把一张纸对折……一张纸很普通?科学家:如果将它对折103次……超出宇宙的可观测直径930亿光年总结:(1)y=1.11x,x∈[0,+∞)(2)(3)y=2x,∈N* y=ax指数x是自变量指 数 函 数的 概 念:一般地,函数y=ax(a>0且a≠1)叫做指数函数,其中指数x是自变量,定义域是R.
0
1
a
为什么规定呢?
若
若
0的正分数指数幂等于0,0的负分数指数幂没有意义
函数形式上有什么特征?
因此,指数函数的定义只是一个形式定义.判断一个函数是不是指数函数关键是看这个函数的解析式变形整理之后是不是具备以上三个特征.
典例探究:典例1: 判断下列函数那些是指数函数?① y=-2x; ②y=(-2)x; ③y=(2)-x;④y=2x-1;⑤y=2x(x>0);⑥y=(m-1)x(m>1,m≠2的常数);⑦y=x2;⑧y=2x+1;⑨y=3·2x;答:③⑥是指数函数,其余都不是.典例2: 已知指数函数f(x)=ax(a>0,且a≠1),且f(3)=π,求:f(0),f(1),f(-3)值.解:∵f(x)=ax,且f(3)=π, 则a3=π, 解得∴∴方法总结:待定系数法确定指数函数解析式典例3(1)如果平均每位游客出游一次可给当地带来1000元门票之外的收入,A地景区的门票价格为150元,比较这15年间A,B两地旅游收入变化情况.解:设经过x年,游客给A、B两地带来的收入分别为f(x),g(x),则g(x)=1000×278×1.11x利用计算工具可以算出:当x=0时,f(0)-g(0)=412 000.当x≈10.22时,f(10.22)≈g(10.22).结合右图可知:当x>10.22时,f(x)<g(x).当x<10.22时,f(x)>g(x).当x=14时,g(14)-f(14)≈347 303.答:(1)2001年,游客给A地带来的收入高于B地412000万元;(2)2001后的10年,f(x)>g(x),游客给A地带来的收入仍高于B地,但g(x)比f(x)增长的速度快,大约2011年2月某个时刻就有f(x)=g(x)了,这时游客给A地带来的收入和B地差不多;(3)10年后,f(x)<g(x),游客给B地带来的收入高于了A地,由于g(x)增长的速度越来越快,而f(x)增长的速度不变,到2015年,游客给B地带来的收入已经高于了A地347303万元了.在问题(2)中,某生物死亡10000年后,它体内碳14的含量衰减为原来的百分之几? 在实际问题中,经常会遇到类似于例题3中的指数增长模型:设原有量为N,每次的增长率为p,经过x次增长,该量增长到y,则y=N(1+p)x,x∈N.形如y=kax(k∈R,且k≠0,a>0,且a≠1)的函数是刻画指数增长或指数衰减变化规律的非常有用的函数模型.课堂练习:1.函数y=(2a-3)ax是指数函数,则f(1)=( ) 答案:D2.已知函数f(x)=(2a-1)x是指数函数,则a的取值范围是______ 3.随着我国经济的不断发展,2014年年底某偏远地区的农民人均年收入为3000元,预计该地区今后的农民的人均年收入将以6%的平均增长率增加,那么2021年年底该地区的农民人均年收入为( ) 答案:B4.调查表明:酒后驾驶是导致交通事故的主要原因,交通法规规定:驾驶员在驾驶机动车时,血液中的酒精含量不得超过0.2mg/ml,如果某人喝了少量酒后,血液中的酒精含量将迅速上升到0.8mg/ml,在停止喝酒后,血液中的酒精含量将以每小时50%的速度减少,则他至少经过多少小时后才可以驾驶机动车 解:设经过x个小时后才可以驾驶机动车,由题意得,【归纳小节】
1.指数函数的定义
一般的,函数 叫做指数函数,其中指数是自变量,定义域是R
2.指数函数形式上有什么特征
3.理解指数函数模型。
分层作业2:三二小本261页,营养提升练
10题,11题。(选做)
分层作业1:三二大本任务学习一和二。(必做)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
